परिचय

एक शिक्षक के बिना मशीन सीखने के तरीकों के बारे में मेरे पिछले लेख में, मूल SOINN एल्गोरिथ्म पर विचार किया गया था - बढ़ते तंत्रिका नेटवर्क के स्व-आयोजन के लिए एक एल्गोरिथ्म। जैसा कि उल्लेख किया गया है, SOINN नेटवर्क के मूल मॉडल में कई कमियां हैं जो इसे आजीवन मोड में सीखने के लिए उपयोग करने की अनुमति नहीं देता है (यानी, नेटवर्क के पूरे जीवन के दौरान सीखने के लिए)। इन नुकसानों में दो-परत नेटवर्क संरचना शामिल थी, जिसके लिए नेटवर्क की पहली परत में दूसरी परत को पूरी तरह से वापस लेने के लिए मामूली बदलाव की आवश्यकता होती है। एल्गोरिथ्म में कई विन्यास योग्य पैरामीटर भी थे, जो वास्तविक डेटा के साथ काम करते समय उपयोग करना मुश्किल बना देता था।

यह लेख एन एन्हांसड सेल्फ-ऑर्गेनाइजिंग इन्क्रीमेंटल न्यूरल नेटवर्क एल्गोरिथ्म पर चर्चा करेगा, जो मूल SOINN मॉडल का एक विस्तार है और आंशिक रूप से आवाज की गई समस्याओं को हल करता है।

SOINN वर्ग एल्गोरिदम का सामान्य विचार

सभी SOINN एल्गोरिदम का मुख्य विचार सिस्टम द्वारा प्रदान की गई छवियों के आधार पर एक संभाव्य डेटा मॉडल का निर्माण करना है। सीखने की प्रक्रिया में, SOINN वर्ग के एल्गोरिदम एक ग्राफ का निर्माण करते हैं, जिनमें से प्रत्येक शीर्ष पर स्थानीयता की अधिकतम संभावना घनत्व के क्षेत्र में होती है, और किनारों को एक ही वर्ग से संबंधित कोने जोड़ता है। इस दृष्टिकोण का अर्थ यह है कि कक्षाएं अंतरिक्ष में उच्च संभावना घनत्व के क्षेत्र बनाती हैं, और हम एक ऐसा ग्राफ बनाने की कोशिश कर रहे हैं जो ऐसे क्षेत्रों और उनके सापेक्ष पदों का सटीक रूप से वर्णन करता है। इस विचार को इस प्रकार चित्रित किया जा सकता है:

1) आने वाले इनपुट डेटा के लिए, एक ग्राफ का निर्माण किया जाता है ताकि स्थानीयता अधिकतम घनत्व घनत्व के क्षेत्र में आ जाए। तो हमें एक ग्राफ मिलता है, जिसके प्रत्येक शीर्ष पर हम कुछ फ़ंक्शन का निर्माण कर सकते हैं जो अंतरिक्ष के संबंधित क्षेत्र में इनपुट डेटा के वितरण का वर्णन करता है।

2) एक संपूर्ण के रूप में ग्राफ वितरण का मिश्रण है, जिसका विश्लेषण करके, आप स्रोत डेटा में कक्षाओं की संख्या, उनके स्थानिक वितरण और अन्य विशेषताओं को निर्धारित कर सकते हैं।

ESOINN एल्गोरिथम

अब हम ESOINN एल्गोरिथ्म पर चलते हैं। जैसा कि पहले उल्लेख किया गया है, ESOINN एल्गोरिथ्म बढ़ते तंत्रिका नेटवर्क को स्व-व्यवस्थित करने के लिए बुनियादी शिक्षण एल्गोरिथ्म का एक व्युत्पन्न है। मूल SOINN एल्गोरिथ्म की तरह, प्रश्न में एल्गोरिथ्म का उद्देश्य ऑनलाइन (और यहां तक ​​कि जीवन भर) शिक्षक के बिना और सीखने के अंतिम लक्ष्य के बिना सीखना है। ESOINN और पहले से चर्चा किए गए एल्गोरिथ्म के बीच मुख्य अंतर यह है कि नेटवर्क संरचना एकल-परत है और परिणामस्वरूप एल्गोरिथ्म के पूरे संचालन के दौरान सीखने में कम विन्यास पैरामीटर और अधिक लचीलापन है। इसके अलावा, कोर नेटवर्क के विपरीत, जहां जीतने वाले नोड्स हमेशा एक किनारे से जुड़े होते थे, उन्नत एल्गोरिथ्म में, एक कनेक्शन बनाने के लिए एक शर्त दिखाई दी, जिसमें वर्गों के आपसी व्यवस्था को ध्यान में रखते हुए विजेता नोड होते हैं। इस तरह के नियम को जोड़ने से एल्गोरिथ्म को करीब और आंशिक रूप से अतिव्यापी कक्षाओं को सफलतापूर्वक अलग करने की अनुमति मिलती है। इस प्रकार, ESOINN एल्गोरिथ्म मूल SOINN एल्गोरिथ्म में पहचानी गई समस्याओं को हल करने का प्रयास करता है।

अगला, ESOINN नेटवर्क निर्माण एल्गोरिथ्म पर विस्तार से विचार किया जाएगा।

ब्लॉक आरेख

एल्गोरिथम विवरण

संकेतन का उपयोग किया

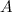
- ग्राफ नोड्स का एक सेट।
- ग्राफ के किनारों का एक सेट।
- में नोड्स की संख्या ।
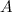
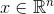
- एल्गोरिथ्म के इनपुट के लिए प्रस्तुत वस्तु की सुविधाओं के वेक्टर।
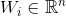
ग्राफ के ith शीर्ष के संकेतों के वेक्टर है।
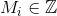
- ग्राफ के आई-वें वर्टेक्स के संचित संकेतों की संख्या।
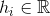
ग्राफ के ith शीर्ष पर घनत्व है।

एल्गोरिथ्म

1. नोड्स के एक सेट को प्रारंभ करें 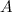स्वीकार्य मानों की सीमा से यादृच्छिक रूप से लिए गए फ़ीचर वैक्टर के साथ दो नोड्स।
   प्रारंभिक संबंध सेट करें 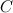खाली सेट।
   
2. इनपुट ऑब्जेक्ट के इनपुट फीचर वेक्टर को सबमिट करें ।
   
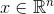3. निकटतम नोड का पता लगाएं (विजेता) और दूसरा निकटतम नोड (दूसरा विजेता), जैसा:
   
   
   
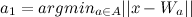
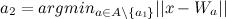
4. यदि इनपुट ऑब्जेक्ट के फीचर वेक्टर के बीच की दूरी और या कुछ दी गई सीमा से अधिक या 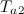, तो यह एक नया नोड पैदा करता है (एक नया नोड जोड़ें) 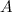और चरण 2 पर जाएं)।
   और 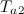सूत्रों द्वारा गणना:
   (यदि शीर्ष में पड़ोसी हैं)
   (यदि शीर्ष पर कोई पड़ोसी नहीं है)
   
5. से आने वाले सभी किनारों की आयु बढ़ाएं 1 से।
   
6. एल्गोरिथ्म 2 का उपयोग करना, निर्धारित करें कि क्या बीच का कनेक्शन है और :
   
   1. यदि आवश्यक हो: अगर रिब मौजूद है, तो उसकी उम्र को शून्य करें, अन्यथा एक बढ़त बनाएं और उसकी उम्र 0 पर सेट की।
      
   2. यदि यह आवश्यक नहीं है: यदि कोई किनारे मौजूद है, तो इसे हटा दें।
      
   
   
7. सूत्र द्वारा विजेता द्वारा संचित संकेतों की संख्या बढ़ाएँ: ।
   
8. सूत्र द्वारा विजेता घनत्व अपडेट करें: 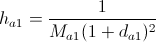जहाँ 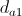- क्लस्टर के भीतर नोड्स के बीच की औसत दूरी जिसमें विजेता होता है। इसकी गणना सूत्र द्वारा की जाती है: ।
   
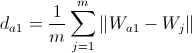9. वजन गुणांक के साथ विजेता और उसके सामयिक पड़ोसियों के विशेषता वैक्टर को अपनाना और 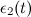सूत्रों के अनुसार:
   
   
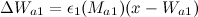
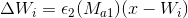
   हम मूल SOINN एल्गोरिथ्म में उसी अनुकूलन योजना को लागू करते हैं:
   
   
   
10. उन पसलियों को ढूंढें और निकालें जिनकी उम्र एक निश्चित सीमा मूल्य से अधिक है ।
    
11. यदि अब तक उत्पन्न इनपुट संकेतों की संख्या कुछ पैरामीटर का गुणक है तब:
    
    1. एल्गोरिथ्म 1 का उपयोग करके सभी नोड्स के लिए वर्ग लेबल अपडेट करें।
       
    2. उन नोड्स को निकालें जो निम्नानुसार हैं:
       
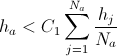       1. सभी नोड्स के लिए से : यदि नोड में दो पड़ोसी हैं और फिर इस नोड को हटा दें।
          
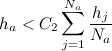       2. सभी नोड्स के लिए से : यदि नोड में एक पड़ोसी और है फिर इस नोड को हटा दें।
          
       3. सभी नोड्स के लिए से : यदि नोड का कोई पड़ोसी नहीं है, तो उसे हटा दें।
          
       
       
    
    
12. यदि सीखने की प्रक्रिया पूरी हो जाती है, तो विभिन्न वर्गों के नोड्स को वर्गीकृत करें (ग्राफ़ के संबंधित घटकों को निकालने के लिए एल्गोरिथ्म का उपयोग करके), और फिर कक्षाओं की संख्या, प्रत्येक कक्षा के लिए एक प्रोटोटाइप वेक्टर की रिपोर्ट करें और सीखने की प्रक्रिया को रोक दें।
    
13. यदि सीखने की प्रक्रिया अभी पूरी नहीं हुई है, तो शिक्षक के बिना सीखने को जारी रखने के लिए चरण 2 पर जाएँ।
    

एल्गोरिथम 1: उपवर्गों में एक समग्र वर्ग का विभाजन

1. हम कहते हैं कि एक नोड एक वर्ग का एक शीर्ष है यदि इसमें पड़ोस में अधिकतम घनत्व है। एक समग्र कक्षा में ऐसे सभी कोने खोजें और उन्हें विभिन्न लेबल असाइन करें।
   
2. शेष वर्धमानों को समान वर्धमानों के समान वर्गों में असाइन करें।
   
3. नोड्स अतिव्यापी वर्गों के क्षेत्र में झूठ बोलते हैं यदि वे विभिन्न वर्गों से संबंधित हैं और एक आम बढ़त है।
   

व्यवहार में, वर्ग को उपवर्गों में विभाजित करने का यह तरीका इस तथ्य की ओर जाता है कि शोर की उपस्थिति में एक बड़े वर्ग को कई छोटे वर्गों के रूप में गलत तरीके से वर्गीकृत किया जा सकता है। इसलिए, कक्षाओं को अलग करने से पहले, आपको उन्हें सुचारू करने की आवश्यकता है।

मान लें कि हमारे पास दो गैर-चिकनी कक्षाएं हैं:

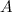
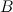
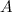
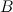
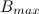
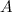
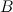
एक उपवर्ग लें और उपवर्ग । मान लें कि उपवर्ग के शीर्ष के घनत्व के बराबर है , और उपवर्ग के बराबर है । एकजुट और यदि निम्न स्थितियाँ सत्य हैं, तो एक उपवर्ग में:

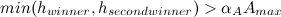
या

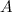
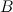
यहाँ पहला और दूसरा विजेता अतिव्यापी उपवर्गों के क्षेत्र में स्थित है और । पैरामीटर गणना इस प्रकार है:
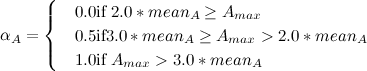
जहाँ - एक उपवर्ग में नोड्स की औसत घनत्व ।

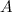
उसके बाद, हम विभिन्न वर्गों के कोने को जोड़ने वाले सभी किनारों को हटा देते हैं। इस प्रकार, हम समग्र वर्ग को उपवर्गों में विभाजित करते हैं जो ओवरलैप नहीं होते हैं।

एल्गोरिथम 2: कोने के बीच संबंध बनाना

दो नोड्स को कनेक्ट करें यदि:

1. उनमें से कम से कम एक नया नोड है (यह अभी तक निर्धारित नहीं है कि यह किस उपवर्ग का है)।
   
2. वे एक ही वर्ग के हैं।
   
3. वे विभिन्न वर्गों से संबंधित हैं, और इन वर्गों को विलय करने की शर्तें पूरी होती हैं ( एल्गोरिथम 1 से स्थितियां)।
   

अन्यथा, हम इन नोड्स को कनेक्ट नहीं करते हैं, और यदि उनके बीच कोई संबंध है, तो हम इसे हटा देते हैं।

नोड्स के बीच एक बढ़त बनाने की आवश्यकता की जांच करते समय एलगोरिदम 1 के उपयोग के लिए धन्यवाद, ईएसओएनएन एल्गोरिथम कक्षाओं के अत्यधिक अलगाव और विभिन्न वर्गों के संयोजन के बीच एक "संतुलन" खोजने की कोशिश करेगा। यह संपत्ति सफल होने के लिए निकटवर्ती वर्गों के क्लस्टरिंग की अनुमति देती है।

एल्गोरिथम चर्चा

ऊपर दिखाए गए एल्गोरिथ्म का उपयोग करते हुए, हम पहली बार इनपुट सिग्नल के निकटतम फीचर वैक्टर के साथ एक जोड़ी वर्टिस पाते हैं। फिर हम तय करते हैं कि इनपुट सिग्नल पहले से ज्ञात वर्गों में से एक है या क्या यह एक नए वर्ग का प्रतिनिधि है। इस प्रश्न के उत्तर के आधार पर, हम या तो नेटवर्क में एक नया वर्ग बनाते हैं या इनपुट संकेत के अनुरूप पहले से ज्ञात वर्ग को समायोजित करते हैं। इस घटना में कि सीखने की प्रक्रिया काफी समय से चल रही है, नेटवर्क अपनी संरचना को समायोजित करता है, डिस्मिलर को अलग करता है और समान उपवर्गों को जोड़ता है। प्रशिक्षण पूरा होने के बाद, हम सभी नोड्स को अलग-अलग कक्षाओं में वर्गीकृत करते हैं।

जैसा कि आप देख सकते हैं, इसके काम की प्रक्रिया में, नेटवर्क नई जानकारी सीख सकता है, जबकि वह सब कुछ नहीं भूल सकता है जो उसने पहले सीखा था। यह संपत्ति कुछ हद तक स्थिरता-प्लास्टिसिटी दुविधा को हल करने की अनुमति देती है और ईएसओएनएन नेटवर्क को जीवन भर के प्रशिक्षण के लिए उपयुक्त बनाती है।

प्रयोगों

प्रस्तुत एल्गोरिथ्म के साथ प्रयोगों का संचालन करने के लिए, इसे बू ग्राफ़ लाइब्रेरी का उपयोग करके C ++ में लागू किया गया था। कोड GitHub पर पोस्ट किया गया है ।

प्रयोगों के लिए एक मंच के रूप में, साइट kaggle.com पर MNIST के आधार पर हस्तलिखित संख्याओं के वर्गीकरण के लिए एक प्रतियोगिता आयोजित की गई थी। प्रशिक्षण डेटा में हस्तलिखित संख्या 28x28 पिक्सेल की 48,000 छवियां और भूरे रंग के 256 शेड हैं, जिन्हें 784-आयामी वैक्टर के रूप में प्रस्तुत किया गया है।

हमने एक गैर-स्थिर वातावरण में वर्गीकरण परिणाम प्राप्त किया (यानी, परीक्षण नमूने के वर्गीकरण के दौरान, नेटवर्क ने सीखना जारी रखा)।

नेटवर्क मापदंडों को निम्नानुसार लिया गया था:
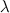
= 200
= ५०
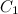
= 0.0001
= 1.0

काम के परिणामस्वरूप, नेटवर्क ने 14 समूहों की पहचान की जिनके केंद्र निम्नानुसार हैं:


लेखन के समय, ESOINN ने परीक्षण नमूने के 25% के लिए 0.96786 की सटीकता के साथ रैंकिंग में एक सम्मानजनक 191 स्थान पर कब्जा कर लिया, जो कि एल्गोरिथ्म के लिए इतना बुरा नहीं है कि शुरू में इनपुट डेटा के बारे में कोई प्राथमिक जानकारी नहीं है।

निष्कर्ष

इस लेख ने ESOINN बढ़ते तंत्रिका नेटवर्क के लिए एक संशोधित लर्निंग एल्गोरिदम की जांच की। मूल SOINN एल्गोरिथ्म के विपरीत, ESOINN एल्गोरिथ्म में केवल एक परत होती है और इसे जीवनकाल प्रशिक्षण के लिए उपयोग किया जा सकता है। इसके अलावा, ESOINN एल्गोरिथ्म आपको आंशिक रूप से अतिव्यापी और फजी वर्गों के साथ काम करने की अनुमति देता है, जो कि एल्गोरिथ्म का मूल संस्करण नहीं कर पाया था। एल्गोरिथ्म मापदंडों की संख्या आधी कर दी गई थी, जो वास्तविक डेटा के साथ काम करते समय नेटवर्क को कॉन्फ़िगर करना आसान बनाता है। प्रयोग ने माना एल्गोरिथ्म का प्रदर्शन दिखाया।

साहित्य

1. शेन फुरोआ, तोमोताका ओगुरब, ओसामु हसेगाबब, 2007 "ऑनलाइन अप्रूव्ड लर्निंग के लिए एक वृद्धिशील स्व-व्यवस्थित वृद्धिशील नेटवर्क ।"
   
2. IIT बॉम्बे में टोक्यो इंस्टीट्यूट ऑफ टेक्नोलॉजी से ओसामु हसेगावा द्वारा वितरित SOINN पर एक बात।
   
3. IIT बॉम्बे में टोक्यो इंस्टीट्यूट ऑफ टेक्नोलॉजी से ओसामु हसेगावा द्वारा वितरित SOINN पर एक चर्चा (वीडियो)।
   
4. हसेगावा लैब की साइट, बढ़ते तंत्रिका नेटवर्क के स्व-आयोजन के लिए एक अनुसंधान प्रयोगशाला।