जेपीईजी का आविष्कार

आप नाम से ठीक से समझ गए कि यह जेपीईजी एल्गोरिथ्म का सामान्य विवरण नहीं है (मैंने "डम्पीज़ के लिए जेपीईजी डिकोडिंग" लेख में विस्तार से फ़ाइल प्रारूप का वर्णन किया है)। सबसे पहले, प्रस्तुति का चुना हुआ तरीका बताता है कि हम न केवल जेपीईजी के बारे में, बल्कि फूरियर ट्रांसफॉर्म और हफ़्फ़ कोडिंग के बारे में भी कुछ नहीं जानते हैं। और सामान्य तौर पर, व्याख्यान से थोड़ा याद किया जाता है। उन्होंने सिर्फ तस्वीर ली और सोचने लगे कि इसे कैसे संपीड़ित किया जा सकता है। इसलिए, मैंने एक सुलभ तरीके से केवल सार को व्यक्त करने की कोशिश की, लेकिन जिसमें पाठक काफी गहरी और, सबसे महत्वपूर्ण बात, एल्गोरिथम की सहज समझ विकसित करेगा। सूत्र और गणितीय गणना - बहुत कम से कम, केवल वही जो समझने के लिए महत्वपूर्ण हैं कि क्या हो रहा है।

JPEG एल्गोरिदम का ज्ञान न केवल छवि संपीड़न के लिए बहुत उपयोगी है। यह डिजिटल सिग्नल प्रोसेसिंग, गणितीय विश्लेषण, रैखिक बीजगणित, सूचना सिद्धांत, विशेष रूप से, फूरियर ट्रांसफॉर्म, दोषरहित कोडिंग, आदि के सिद्धांत का उपयोग करता है, इसलिए प्राप्त ज्ञान कहीं भी उपयोगी हो सकता है।

अगर कोई इच्छा है, तो मैं स्वतंत्र रूप से लेख के साथ समान चरणों में जाने का प्रस्ताव करता हूं। जांचें कि उपरोक्त तर्क विभिन्न छवियों के लिए कैसे उपयुक्त है, एल्गोरिथ्म में अपने संशोधन करने का प्रयास करें। यह बहुत दिलचस्प है। एक उपकरण के रूप में, मैं पायथन + न्यूमपी + मैटलपोटलिब + पीआईएल (पिलो) के एक अद्भुत समूह की सिफारिश कर सकता हूं। मेरे लगभग सभी काम (ग्राफिक्स और एनीमेशन सहित) उनका उपयोग करके किया गया था।

चेतावनी यातायात! कई चित्र, रेखांकन और एनिमेशन (~ 10Mb)। विडंबना यह है कि जेपीईजी के बारे में लेख में पचास से इस प्रारूप के साथ केवल 2 छवियां हैं।

जानकारी को संपीड़ित करने के लिए जो कुछ भी एल्गोरिदम है, उसका सिद्धांत हमेशा एक ही होगा - पैटर्न का पता लगाना और वर्णन करना। अधिक पैटर्न, अधिक अतिरेक, कम जानकारी। अभिलेखागार और एनकोडर आमतौर पर एक विशिष्ट प्रकार की जानकारी के लिए "सिलवाया" जाते हैं, और जानते हैं कि उन्हें कहां खोजना है। कुछ मामलों में, पैटर्न तुरंत दिखाई देता है, उदाहरण के लिए, नीले आकाश की तस्वीर। इसके डिजिटल प्रतिनिधित्व की प्रत्येक पंक्ति को एक सीधी रेखा द्वारा काफी सटीक रूप से वर्णित किया जा सकता है।

हम बिल्लियों के रैकून पर प्रशिक्षण देंगे। ऊपर दी गई ग्रे इमेज को एक उदाहरण के रूप में लिया गया है। यह सजातीय और विपरीत दोनों क्षेत्रों को अच्छी तरह से जोड़ती है। और अगर हम ग्रे को संपीड़ित करना सीखते हैं, तो रंग के साथ कोई समस्या नहीं होगी।

सदिश दृश्य

सबसे पहले, जांच लें कि दो पड़ोसी पिक्सेल कितने निर्भर हैं। यह मानना ​​तर्कसंगत है कि सबसे अधिक संभावना है कि वे बहुत समान होंगे। सभी छवि जोड़े के लिए इसे देखें। हम उन्हें डॉट्स के साथ समन्वित विमान पर चिह्नित करते हैं ताकि एक्स अक्ष के साथ बिंदु का मूल्य पहले पिक्सेल का मूल्य हो, वाई अक्ष दूसरे के साथ। 256 के आकार की हमारी छवि के लिए हमें 256 * 256/2 अंक मिलते हैं:

यह अनुमान लगाने योग्य है कि अधिकांश बिंदु सीधी रेखा y = x पर या उसके आस-पास स्थित हैं (और उनमें से भी अधिक हैं जो आंकड़े में देखा जा सकता है, क्योंकि वे कई बार ओवरलैप करते हैं, और, इसके अलावा, वे पारभासी हैं)। और यदि ऐसा है, तो उन्हें 45 ° मोड़कर काम करना आसान होगा। ऐसा करने के लिए, आपको उन्हें एक अलग समन्वय प्रणाली में व्यक्त करने की आवश्यकता है।

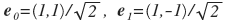
नई प्रणाली के मूल वैक्टर स्पष्ट रूप से ऐसे हैं: । हम एक रूढ़िवादी प्रणाली (आधार वैक्टर की लंबाई एकता के बराबर हैं) प्राप्त करने के लिए दो की जड़ से विभाजित करने के लिए मजबूर हैं। यह यहाँ दिखाया गया है कि नई प्रणाली में कुछ बिंदु p = (x, y) को एक बिंदु ( ₀ , ₁ ) के रूप में दर्शाया जाएगा। नए गुणांक को जानने के बाद, हम पुराने लोगों को रिवर्स रोटेशन द्वारा आसानी से प्राप्त कर सकते हैं। जाहिर है, पहला (नया) समन्वय मध्य है, और दूसरा x और y का अंतर है (लेकिन 2 की जड़ से विभाजित)। कल्पना करें कि आपको मूल्यों में से केवल एक को छोड़ने के लिए कहा गया है: या तो ₀ या ₁ (यानी, दूसरा शून्य के बराबर है)। ₁ को चुनना बेहतर होता है, चूंकि 1 का मान और इसलिए, सबसे अधिक संभावना है, शून्य के पास होगा। यदि हम केवल ₀ पर ही छवि को पुनर्स्थापित करते हैं तो यहां क्या होता है:

4x बढ़ाई:

ईमानदार होने के लिए यह संपीड़न बहुत प्रभावशाली नहीं है। चित्र को समान रूप से पिक्सेल के त्रिभुज में विभाजित करना और उन्हें त्रि-आयामी स्थान में प्रस्तुत करना बेहतर है।

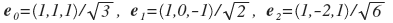
यह एक ही चार्ट है, लेकिन विभिन्न दृष्टिकोणों से। लाल रेखाएं वे अक्ष हैं जो स्वयं का सुझाव देते हैं। वैक्टर उनके अनुरूप हैं: । मैं आपको याद दिलाता हूं कि आपको कुछ स्थिरांक से विभाजित करना होगा ताकि वैक्टर की लंबाई एकता के बराबर हो जाए। इस प्रकार, इस तरह के आधार पर विस्तार करते हुए, हमें ₀ , ₁ , ₂ , और _{0 के} 3 मान मिलते हैं, जो कि _{1 से} अधिक महत्वपूर्ण है, और ₁ एक _{2 की} तुलना में अधिक महत्वपूर्ण है। यदि हम एक ₂ बाहर फेंकते हैं, तो ग्राफ वेक्टर ई ₂ की दिशा में "चपटा" है। यह पहले से ही मोटी नहीं है तीन आयामी चादर सपाट हो जाएगी। वह बहुत कुछ नहीं खोएगा, लेकिन हम एक तिहाई मूल्यों से छुटकारा पा लेंगे। त्रिगुणों से समाहित चित्रों की तुलना करें: ( ₀ , 0, 0), ( ₁ , ₂ , 0), और ( ₀ , ₁ , ₂ )। बाद के संस्करण में, हमने कुछ भी नहीं फेंका, इसलिए हमें मूल मिलता है।

4x बढ़ाई:

दूसरी ड्राइंग पहले से ही अच्छी है। तेज क्षेत्रों को थोड़ा बाहर निकाला गया था, लेकिन कुल मिलाकर तस्वीर को बहुत अच्छी तरह से संरक्षित किया गया था। और अब, उसी तरह हम चार में विभाजित करेंगे और नेत्रहीन रूप से चार-आयामी अंतरिक्ष में एक आधार को परिभाषित करेंगे ... आह, हाँ। लेकिन आप अनुमान लगा सकते हैं कि आधार के वैक्टर में से एक क्या होगा: (1,1,1,1) / 2। इसलिए, हम दूसरों को प्रकट करने के लिए वेक्टर के लिए लंबवत स्पेस पर चार-आयामी अंतरिक्ष का प्रक्षेपण देख सकते हैं। लेकिन यह सबसे अच्छा तरीका नहीं है।
हमारा लक्ष्य यह सीखना है कि कैसे परिवर्तित करें (x ₀ , x ₁ , ..., x _n-1 ) से ( ₀ , ₁ , ₁ , ..., _n-1 ) ताकि प्रत्येक मान _i कम से कम महत्वपूर्ण हो पिछले वाले। यदि हम ऐसा कर सकते हैं, तो शायद अंतिम अनुक्रम मूल्यों को पूरी तरह से फेंक दिया जा सकता है। उपरोक्त प्रयोगों ने संकेत दिया कि यह संभव है। लेकिन एक गणितीय उपकरण के बिना नहीं कर सकता।
तो, आपको बिंदुओं को एक नए आधार में बदलने की आवश्यकता है। लेकिन पहले आपको एक उपयुक्त आधार खोजने की आवश्यकता है। पहले युग्मन प्रयोग पर वापस जाएं। हम इसे सामान्यीकृत मानेंगे। हमने आधार वैक्टर निर्धारित किए:

उनके माध्यम से व्यक्त वेक्टर पी :

या निर्देशांक में:

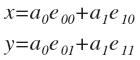₀ और ₁ खोजने के लिए _, आपको क्रमशः e ₀ और e ₁ पर p प्रोजेक्ट करना होगा। और इसके लिए आपको स्केलर उत्पाद खोजने की आवश्यकता है

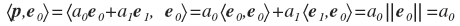
इसी तरह:

निर्देशांक में:

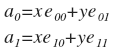
मैट्रिक्स रूप में रूपांतरण करने के लिए अक्सर अधिक सुविधाजनक होता है।

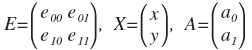
तब A = EX और X = E ^T A. यह एक सुंदर और आरामदायक आकार है। मैट्रिक्स ई को परिवर्तन मैट्रिक्स कहा जाता है और यह ऑर्थोगोनल है, हम अभी भी इसके साथ मिलेंगे।

वैक्टर से कार्यों के लिए संक्रमण।

छोटे आयामों के वैक्टर के साथ काम करना सुविधाजनक है। हालांकि, हम बड़े ब्लॉकों में पैटर्न ढूंढना चाहते हैं, इसलिए एन-आयामी वैक्टर के बजाय छवि को दर्शाने वाले दृश्यों के साथ काम करना अधिक सुविधाजनक है। मैं इस तरह के दृश्यों को असतत कार्य कहूंगा, क्योंकि निम्नलिखित विचार निरंतर कार्यों पर लागू होते हैं।
हमारे उदाहरण पर लौटते हुए, हम एक ऐसा फ़ंक्शन f (i) प्रस्तुत करते हैं, जिसे केवल दो बिंदुओं पर परिभाषित किया गया है: f (0) = x और f (1) = y। हम इसी प्रकार आधार ₀ और ई _{1 के} आधार पर ई ₀ (i) और ई ₁ (i) के आधार कार्यों को परिभाषित करते हैं। हमें मिलता है:

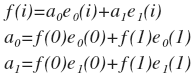
यह एक बहुत महत्वपूर्ण निष्कर्ष है। अब वाक्यांश में "वेक्टर वेक्टर में अपघटन" को "फ़ंक्शन" के साथ "वेक्टर" शब्द को बदल सकते हैं और काफी सही अभिव्यक्ति प्राप्त कर सकते हैं "समारोह में अपघटन के कार्यों में अपघटन"। इससे कोई फर्क नहीं पड़ता है कि हमें ऐसा एक डरावना कार्य मिला है, क्योंकि एन-आयामी वेक्टर के लिए एक ही तर्क काम करता है, जिसे एन मानों के साथ असतत फ़ंक्शन के रूप में दर्शाया जा सकता है। और कार्यों के साथ काम एन-आयामी वैक्टर के साथ अधिक दृश्य है। आप कर सकते हैं, और इसके विपरीत, एक समारोह की कल्पना करें जैसे कि एक वेक्टर। इसके अलावा, एक साधारण निरंतर फ़ंक्शन को एक अनंत-आयामी वेक्टर द्वारा दर्शाया जा सकता है, हालांकि सत्य अब यूक्लिडियन में नहीं है, लेकिन हिल्बर्ट अंतरिक्ष में। लेकिन हम वहां नहीं गए, हम केवल असतत कार्यों में रुचि लेंगे।
और आधार खोजने का हमारा कार्य एक उपयुक्त प्रणाली की काम करने की समस्या में बदल जाता है। निम्नलिखित तर्क में, यह माना जाता है कि हमने किसी तरह आधार कार्यों के एक सेट को परिभाषित किया है जिसके द्वारा हम विघटित होंगे।
मान लें कि हमारे पास कुछ फ़ंक्शन हैं (उदाहरण के लिए, मूल्यों द्वारा) जो हम दूसरों के योग के रूप में प्रतिनिधित्व करना चाहते हैं। आप वेक्टर रूप में इस प्रक्रिया का प्रतिनिधित्व कर सकते हैं। किसी फ़ंक्शन को विघटित करने के लिए, आपको मूल कार्यों में इसे "प्रोजेक्ट" करना होगा। सदिश अर्थ में, प्रक्षेपण की गणना मूल सदिश का न्यूनतम सन्निकटन दूसरे से दूरी में करती है। यह ध्यान में रखते हुए कि दूरी की गणना पायथागॉरियन प्रमेय का उपयोग करके की जाती है, फ़ंक्शन के रूप में एक समान प्रतिनिधित्व दूसरे को फ़ंक्शन का सबसे अच्छा मतलब-वर्ग सन्निकटन देता है। इस प्रकार, प्रत्येक गुणांक (k) फ़ंक्शन की "निकटता" निर्धारित करता है। अधिक औपचारिक रूप से, k * e (x) l * e (x) के बीच f (x) के लिए सबसे अच्छा rms सन्निकटन है।
निम्नलिखित उदाहरण केवल दो बिंदुओं द्वारा एक फ़ंक्शन को अनुमानित करने की प्रक्रिया को दर्शाता है। दाईं ओर एक वेक्टर प्रतिनिधित्व है।

जैसा कि हमारे युग्मन प्रयोग पर लागू होता है, हम कह सकते हैं कि ये दो बिंदु (एब्सिसा में 0 और 1) पड़ोसी पिक्सल (x, y) की एक जोड़ी हैं।
एनीमेशन के साथ एक ही बात:

यदि हम 3 अंक लेते हैं, तो हमें तीन आयामी वैक्टर पर विचार करने की आवश्यकता है, हालांकि, सन्निकटन अधिक सटीक होगा। और एन मूल्यों के साथ असतत कार्य के लिए, किसी को एन-आयामी वैक्टर पर विचार करने की आवश्यकता है।
प्राप्त गुणांक का एक सेट होने के बाद, कोई भी संबंधित गुणांकों के साथ किए गए आधार कार्यों को संक्षेप में करके प्रारंभिक कार्य प्राप्त कर सकता है। इन गुणांक का विश्लेषण बहुत सारी उपयोगी जानकारी (आधार पर निर्भर) प्रदान कर सकता है। इन विचारों का एक विशेष मामला फूरियर विस्तार का सिद्धांत है। आखिरकार, हमारा तर्क किसी भी आधार पर लागू होता है, और फूरियर श्रृंखला में विस्तार करते समय, एक बहुत ही विशिष्ट लिया जाता है।

असतत फूरियर रूपांतरण (DFT)

पिछले भाग में, हम इस निष्कर्ष पर पहुंचे कि फ़ंक्शन को घटकों में विघटित करना अच्छा होगा। 19 वीं शताब्दी की शुरुआत में, फूरियर ने भी इस बारे में सोचा। सच है, उसके पास एक रैकून के साथ एक तस्वीर नहीं थी, इसलिए उसे धातु की अंगूठी के साथ गर्मी के वितरण का अध्ययन करना पड़ा। तब उन्हें पता चला कि विभिन्न अवधियों के साथ साइनसोइड्स के योग के रूप में रिंग के प्रत्येक बिंदु पर तापमान (और इसके परिवर्तन) को व्यक्त करना बहुत सुविधाजनक है। "फूरियर ने स्थापित किया है (मैं इसे पढ़ने की सलाह देता हूं, दिलचस्प है) कि दूसरा हार्मोनिक पहले की तुलना में 4 गुना तेज है, और उच्च-क्रम हार्मोनिक्स भी तेजी से क्षय करता है।"
सामान्य तौर पर, यह जल्द ही पता चला कि आवधिक कार्यों को साइनसोइड्स के योग में उल्लेखनीय रूप से विघटित किया गया था। और चूंकि प्रकृति में आवधिक कार्यों द्वारा वर्णित कई ऑब्जेक्ट और प्रक्रियाएं हैं, उनके विश्लेषण के लिए एक शक्तिशाली उपकरण दिखाई दिया है।
शायद सबसे स्पष्ट आवधिक प्रक्रियाओं में से एक ध्वनि है।

• 1 चार्ट - 2500 हर्ट्ज की आवृत्ति के साथ एक शुद्ध स्वर।
• दूसरा - सफेद शोर। यही है, पूरे रेंज में समान रूप से वितरित आवृत्तियों के साथ शोर।
• 3 - पहले दो का योग।

यदि मुझे उस समय अंतिम समारोह के मूल्य दिए गए थे जब मुझे फूरियर श्रृंखला के बारे में नहीं पता था और उनका विश्लेषण करने के लिए कहा गया था, तो मैं निश्चित रूप से भ्रमित होऊंगा और कुछ भी सार्थक नहीं कह सकता। ठीक है, हाँ, किसी प्रकार का फ़ंक्शन, लेकिन यह कैसे समझें कि वहाँ कुछ ऑर्डर किया गया है? लेकिन अगर मैंने आखिरी समारोह को सुनने का अनुमान लगाया था, तो शोर के बीच मेरा कान एक स्पष्ट स्वर को पकड़ लेगा। हालांकि बहुत अच्छा नहीं है, क्योंकि मैंने पीढ़ी के दौरान विशेष रूप से ऐसे मापदंडों का चयन किया है कि सिग्नल कुल ग्राफ पर शोर में भंग हो गया। जैसा कि मैंने इसे समझा, यह अभी भी तय नहीं है कि हियरिंग एड यह कैसे करता है। हालाँकि, यह हाल ही में स्पष्ट हो गया है कि यह ध्वनि को साइनसोइड में बाहर नहीं करता है । शायद किसी दिन हम समझेंगे कि यह कैसे होता है, और अधिक उन्नत एल्गोरिदम दिखाई देंगे। खैर, जबकि हम पुराने जमाने के हैं।
एक आधार के रूप में साइनसोइड लेने की कोशिश क्यों नहीं की जाती है? वास्तव में, हमने वास्तव में ऐसा किया है। हमारे अपघटन को 3 आधार वैक्टरों में याद करें और ग्राफ पर उनका प्रतिनिधित्व करें:

हां, हां, मुझे पता है, यह एक फिट की तरह दिखता है, लेकिन तीन वैक्टर के साथ यह अधिक उम्मीद करना मुश्किल है। लेकिन अब यह स्पष्ट है कि कैसे प्राप्त करें, उदाहरण के लिए, 8 आधार वैक्टर:

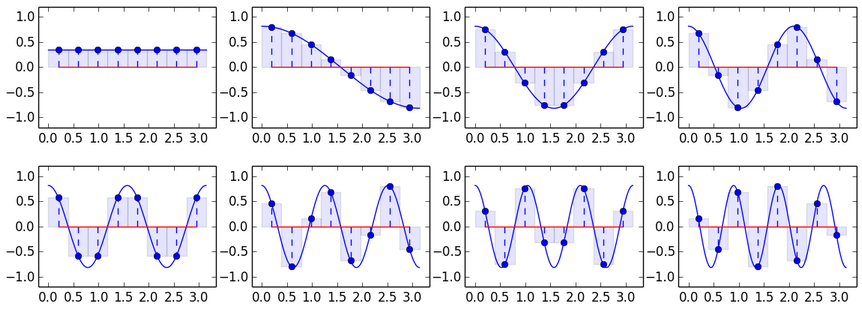
एक बहुत ही जटिल जांच से पता चलता है कि ये वैक्टर जोड़ीदार लंबवत हैं, अर्थात, ऑर्थोगोनल। इसका मतलब है कि उनका उपयोग आधार के रूप में किया जा सकता है। इस तरह के आधार पर एक परिवर्तन व्यापक रूप से जाना जाता है, और एक असतत कोसाइन रूपांतरण (डीसीटी) कहा जाता है। मुझे लगता है कि ग्राफ़ से यह स्पष्ट है कि डीसीटी परिवर्तन सूत्र कैसे प्राप्त किया जाता है:

यह एक ही सूत्र है: A = EX एक प्रतिस्थापित आधार के साथ। संकेतित डीसीटी के बेस वैक्टर (वे मैट्रिक्स ई के पंक्ति वैक्टर भी हैं) ऑर्थोगोनल हैं, लेकिन ऑर्थोनॉनिक नहीं। यह उलटा परिवर्तन में याद किया जाना चाहिए (मैं इस पर ध्यान नहीं दूंगा, लेकिन, कौन परवाह करता है, उलटा डीसीटी की अवधि 0.5 * _{0 है} , क्योंकि शून्य आधार वेक्टर दूसरों की तुलना में बड़ा है)।
निम्न उदाहरण मूल मानों के लिए उप-योगों को अनुमानित करने की प्रक्रिया को दर्शाता है। प्रत्येक पुनरावृत्ति पर, अगले आधार को अगले गुणांक से गुणा किया जाता है और मध्यवर्ती योग में जोड़ा जाता है (अर्थात, एक रैकून पर पिछले प्रयोगों में - मानों का एक तिहाई, दो तिहाई)।

लेकिन, फिर भी, इस तरह के आधार को चुनने की सलाह के बारे में कुछ तर्कों के बावजूद, अभी तक कोई वास्तविक तर्क नहीं हैं। वास्तव में, ध्वनि के विपरीत, आवधिक कार्यों में एक छवि को विघटित करने की उपयुक्तता बहुत कम स्पष्ट है। हालांकि, एक छोटे से क्षेत्र में भी छवि बहुत अप्रत्याशित हो सकती है। इसलिए, तस्वीर को छोटे टुकड़ों में विभाजित किया गया है, लेकिन काफी छोटे नहीं, ताकि अपघटन समझ में आता है। JPEG में, छवि 8x8 वर्गों में "कटा हुआ" है। इस तरह के एक टुकड़े के भीतर, तस्वीरें आमतौर पर बहुत समान होती हैं: पृष्ठभूमि और मामूली उतार-चढ़ाव। ऐसे क्षेत्रों को साइनसोइड द्वारा सुरुचिपूर्ण ढंग से अनुमानित किया जाता है।
खैर, बता दें कि यह तथ्य कमोबेश सहज है। लेकिन तेज रंग संक्रमण के बारे में एक बुरी भावना है, क्योंकि धीरे-धीरे बदलते कार्यों से हमें बचा नहीं होगा। आपको विभिन्न हाई-फ़्रीक्वेंसी फ़ंक्शंस को जोड़ना होगा जो उनके काम का सामना करते हैं, लेकिन एक साथ एक समान पृष्ठभूमि पर दिखाई देते हैं। दो विषम क्षेत्रों के साथ एक 256x256 चित्र लें:

हम डीसीटी का उपयोग करके प्रत्येक पंक्ति को विघटित करते हैं, इस प्रकार प्रति पंक्ति 256 गुणांक प्राप्त करते हैं।
फिर हम केवल पहले n गुणांक छोड़ते हैं, और शेष को शून्य पर सेट करते हैं, और इसलिए, छवि को केवल पहले हार्मोनिक्स के योग के रूप में प्रस्तुत किया जाएगा:

चित्र में संख्या शेष गुणांक की संख्या है। पहली छवि में केवल औसत मूल्य रहता है। दूसरे ने पहले से ही एक कम-आवृत्ति वाली साइन वेव आदि को जोड़ा है, वैसे, सीमा पर ध्यान दें - सर्वश्रेष्ठ सन्निकटन के बावजूद, विकर्ण के बगल में 2 स्ट्रिप्स स्पष्ट रूप से दिखाई देते हैं, एक हल्का है और दूसरा गहरा है। अंतिम छवि का हिस्सा 4 गुना बढ़ गया:

और सामान्य तौर पर, यदि सीमा से दूर हम प्रारंभिक वर्दी की पृष्ठभूमि देखते हैं, तो जब यह निकट आता है, तो आयाम बढ़ने लगता है, अंत में अपने न्यूनतम मूल्य तक पहुंच जाता है, और फिर यह तेजी से अधिकतम हो जाता है। इस घटना को गिब्स प्रभाव के रूप में जाना जाता है।

इन कूबड़ की ऊंचाई, जो फ़ंक्शन की असंतुलन के पास दिखाई देती है, कार्यों की शर्तों की संख्या में वृद्धि के साथ कम नहीं होगी। एक असतत परिवर्तन में, यह केवल गायब हो जाता है जब लगभग सभी गुणांक संरक्षित होते हैं। अधिक सटीक रूप से, यह अदृश्य हो जाता है।
निम्न उदाहरण पूरी तरह से त्रिकोण के उपरोक्त अपघटन के समान है, लेकिन पहले से ही एक वास्तविक रैकून पर है:

डीसीटी का अध्ययन करते समय, यह गलत धारणा दे सकता है कि बस पहले कुछ (कम-आवृत्ति) गुणांक हमेशा पर्याप्त होते हैं। यह तस्वीरों के कई टुकड़ों के लिए सच है, जिनके मूल्य नाटकीय रूप से नहीं बदलते हैं। हालांकि, विषम क्षेत्रों की सीमा पर, मूल्य नाटकीय रूप से कूदेंगे और यहां तक ​​कि अंतिम गुणांक बड़े होंगे। इसलिए, जब आप डीसीटी ऊर्जा संरक्षण संपत्ति के बारे में सुनते हैं, तो इस तथ्य के लिए भत्ता बनाएं कि यह कई प्रकार के संकेतों पर लागू होता है, लेकिन सभी के लिए नहीं। एक उदाहरण के रूप में, इस बारे में सोचें कि एक असतत फ़ंक्शन कैसा दिखेगा, जिसके विस्तार गुणांक शून्य के बराबर हैं, पिछले एक को छोड़कर। संकेत: वेक्टर रूप में अपघटन की कल्पना करें।
कमियों के बावजूद, चुना गया आधार वास्तविक तस्वीरों में सर्वश्रेष्ठ में से एक है। थोड़ी देर बाद हम दूसरों के साथ एक छोटी सी तुलना देखेंगे।

डीसीटी बनाम बाकी सब

जब मैंने ऑर्थोगोनल परिवर्तनों के मुद्दे का अध्ययन किया, तो ईमानदार होने के लिए, मैं इस तर्क से बहुत आश्वस्त नहीं था कि चारों ओर सब कुछ हार्मोनिक दोलनों का योग है, इसलिए मुझे साइनसोइड में चित्रों को विघटित करने की आवश्यकता है। या शायद कुछ कदम कार्य बेहतर हैं? इसलिए, मैं वास्तविक छवियों में डीसीटी की इष्टतमता पर शोध परिणामों की तलाश कर रहा था। तथ्य यह है कि "यह डीसीटी है जो" ऊर्जा संघनन "संपत्ति" के कारण व्यावहारिक अनुप्रयोगों में सबसे अधिक बार पाया जाता है। इस गुण का अर्थ है कि जानकारी की अधिकतम मात्रा पहले गुणांक में निहित है। और क्यों? एक अध्ययन का संचालन करना मुश्किल नहीं है: हम विभिन्न चित्रों, विभिन्न प्रसिद्ध ठिकानों के एक समूह के साथ खुद को बांधा करते हैं और विभिन्न गुणांक के लिए वास्तविक छवि से मानक विचलन पर विचार करना शुरू करते हैं। इस तकनीक पर लेख ( यहां छवियों का उपयोग किया गया ) में थोड़ा शोध किया। इसमें विभिन्न आधारों पर पहले अपघटन गुणांक की संख्या पर संग्रहीत ऊर्जा की निर्भरता के ग्राफ शामिल हैं। यदि आपने रेखांकन देखा, तो आप आश्वस्त थे कि DCT लगातार माननीय ... um ... तृतीय स्थान लेता है। ऐसा कैसे? केएलटी रूपांतरण किस तरह का है? मैंने DCT की प्रशंसा की, और यहाँ ...

KLT

KLT को छोड़कर सभी परिवर्तन निरंतर आधार परिवर्तन हैं। और KLT में (करुणेन-लोव परिवर्तन) कई वैक्टरों के लिए सबसे इष्टतम आधार की गणना की जाती है। यह इस तरह से गणना की जाती है कि पहले गुणांक सभी वैक्टर के लिए कुल मिलाकर सबसे छोटी मानक त्रुटि देगा। हमने पहले मैन्युअल रूप से इसी तरह का काम किया, आधार को नेत्रहीन रूप से निर्धारित किया। सबसे पहले यह एक ध्वनि विचार की तरह लगता है। उदाहरण के लिए, हम छवि को छोटे वर्गों में विभाजित कर सकते हैं और प्रत्येक के लिए अपने आधार की गणना कर सकते हैं।लेकिन न केवल इस आधार को संग्रहीत करने के लिए एक चिंता है, बल्कि इसकी गणना का संचालन भी काफी समय लेने वाला है। और DCT केवल एक छोटा खो देता है, और इसके अलावा, DCT में तेजी से रूपांतरण एल्गोरिदम हैं।

एफ टी

DFT (असतत फूरियर ट्रांसफॉर्म) - असतत फूरियर ट्रांसफॉर्म। यह नाम कभी-कभी न केवल एक विशिष्ट परिवर्तन को संदर्भित करता है, बल्कि असतत परिवर्तन (डीसीटी, डीएसटी ...) के पूरे वर्ग को संदर्भित करता है। आइए देखें डीएफटी फॉर्मूला: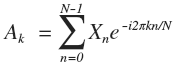

जैसा कि आप कल्पना कर सकते हैं, यह किसी प्रकार का जटिल आधार है। चूंकि ऐसा जटिल रूप हमेशा से थोड़ा अधिक पाया जाता है, इसलिए इसके निष्कर्ष का अध्ययन करने के लिए समझ में आता है।
ऐसा लग सकता है कि डीसीटी अपघटन के दौरान कोई भी शुद्ध हार्मोनिक सिग्नल (पूर्णांक आवृत्ति के साथ) इस हार्मोनिक के अनुरूप केवल एक गैर-अक्षीय गुणांक का उत्पादन करेगा। ऐसा नहीं है, चूंकि आवृत्ति के अलावा, इस संकेत का चरण भी महत्वपूर्ण है। उदाहरण के लिए, कोसाइन में साइन का विस्तार (असतत विस्तार में) इस तरह होगा:

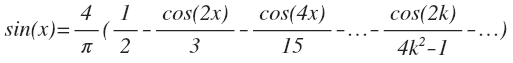यहाँ आपके पास शुद्ध हारमोनिका है। उसने दूसरों का झुंड काट लिया। एनीमेशन विभिन्न चरणों में डीसीटी साइनसोइडल गुणांक दिखाता है।

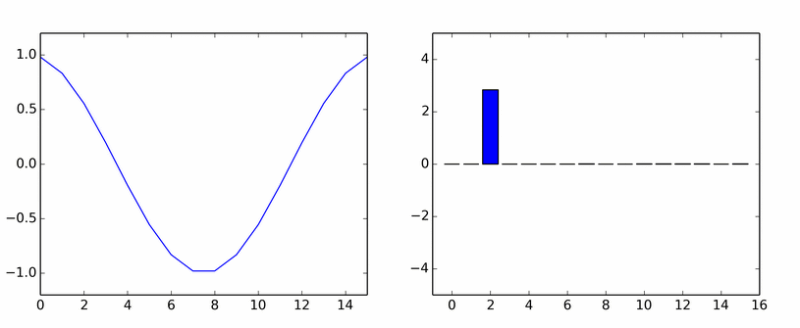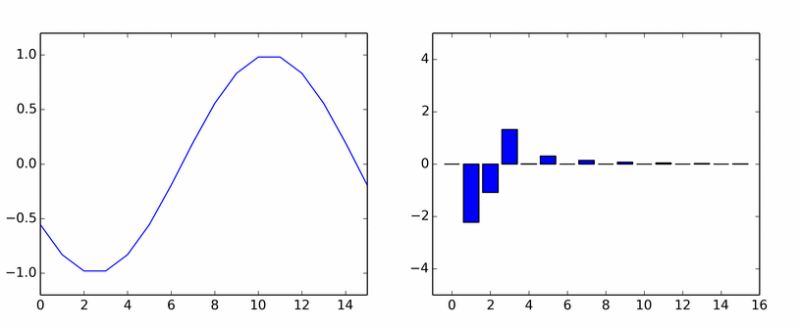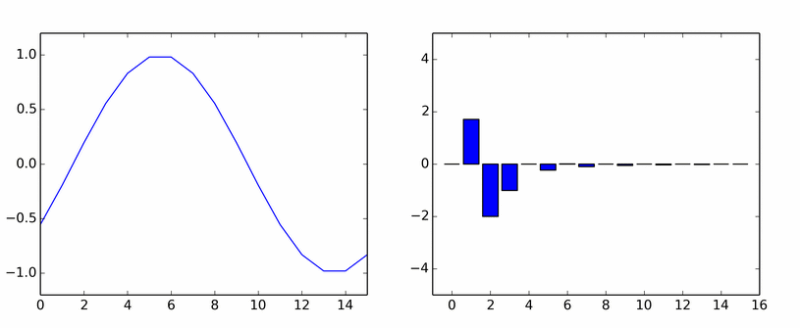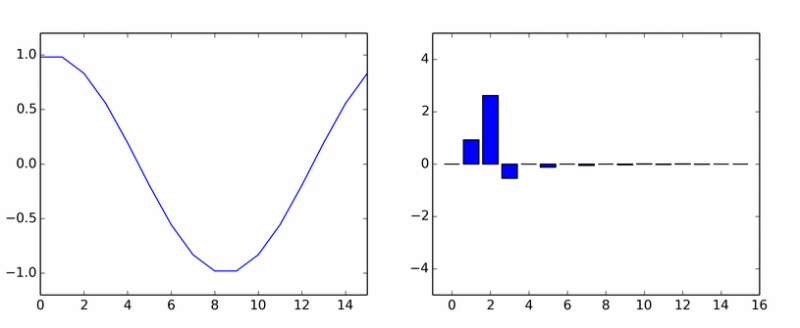यदि आपको ऐसा लगता है कि स्तंभ एक अक्ष के चारों ओर घूमते हैं, तो यह आपको नहीं लगता है।
इसलिए अब हम फ़ंक्शन को केवल अलग-अलग आवृत्तियों के न केवल साइनसोइड्स के योग में विघटित करेंगे, बल्कि कुछ चरण द्वारा स्थानांतरित कर दिया जाएगा। कोसाइन के उदाहरण का उपयोग करके चरण शिफ्ट पर विचार करना अधिक सुविधाजनक होगा:

एक साधारण त्रिकोणमितीय पहचान एक महत्वपूर्ण परिणाम देती है: चरण शिफ्ट को कॉइन और गुणांक कॉस (ख) और पाप (बी) के साथ लिए गए कोइन के योग द्वारा प्रतिस्थापित किया जाता है। तो, आप साइन और कॉशन (बिना किसी चरण के) के योग में कार्यों को विघटित कर सकते हैं। यह एक सामान्य त्रिकोणमितीय रूप है। हालाँकि, एकीकृत अधिक सामान्यतः उपयोग किया जाता है। इसे प्राप्त करने के लिए, आपको यूलर सूत्र का उपयोग करने की आवश्यकता है। बस साइन और कोसाइन के लिए व्युत्पन्न फ़ार्मुलों को प्रतिस्थापित करें, हमें मिलता है: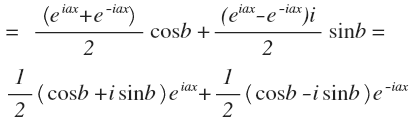

अब एक छोटा प्रतिस्थापन। शीर्ष रेखांकन एक संयुग्म संख्या है।

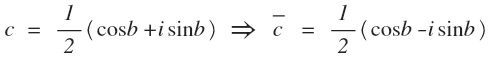हम अंतिम समानता प्राप्त करते हैं:

सी जटिल गुणांक है, जिसका वास्तविक भाग कोसाइन गुणांक के बराबर है, और काल्पनिक - साइन के लिए। और बिंदुओं का समूह (cos (b), sin (b)) एक चक्र है। इस तरह के रिकॉर्ड में, प्रत्येक हार्मोनिक सकारात्मक और नकारात्मक दोनों आवृत्तियों के साथ अपघटन में प्रवेश करता है। इसलिए, फूरियर विश्लेषण के विभिन्न फ़ार्मुलों में, आमतौर पर माइनस से प्लस इन्फिनिटी के लिए योग या एकीकरण होता है। ऐसे जटिल रूप में गणना करना अक्सर अधिक सुविधाजनक होता है।
रूपांतरण सिग्नल क्षेत्र में एक से एन दोलनों तक आवृत्तियों के साथ हार्मोनिक्स में संकेत को विघटित करता है। लेकिन सिग्नल क्षेत्र पर नमूना दर एन है। और Kotelnikov प्रमेय (उर्फ न्यक्विस्ट-शैनन प्रमेय) के अनुसार, नमूना आवृत्ति सिग्नल की आवृत्ति से कम से कम दो बार होनी चाहिए। यदि ऐसा नहीं है, तो एक झूठी आवृत्ति के साथ एक संकेत की उपस्थिति का प्रभाव प्राप्त होता है:

धराशायी लाइनें गलत तरीके से बहाल संकेत दिखाती हैं। आप अक्सर जीवन में इस घटना के पार आए हैं। उदाहरण के लिए, एक वीडियो पर एक कार के पहियों का एक अजीब आंदोलन, या एक गंभीर प्रभाव।
यह इस तथ्य की ओर जाता है कि एन कॉम्प्लेक्स एमिटिट्यूड की दूसरी छमाही अन्य आवृत्तियों से मिलकर लगती है। दूसरी छमाही के ये झूठे सामंजस्य पहले की एक दर्पण छवि हैं और अतिरिक्त जानकारी नहीं रखते हैं। इस प्रकार, हमारे पास अभी भी एन / 2 कोसाइन और एन / 2 साइन हैं (एक ऑर्थोगोनल आधार)।
ठीक है, एक आधार है। इसके घटक सिग्नल क्षेत्र में दोलनों की एक पूर्णांक संख्या के साथ हार्मोनिक्स हैं, जिसका अर्थ है कि हार्मोनिक्स के चरम मूल्य समान हैं। अधिक सटीक रूप से, वे लगभग बराबर हैं, चूंकि अंतिम मूल्य पूरी तरह से किनारे से नहीं लिया गया है। इसके अलावा, प्रत्येक हार्मोनिक अपने केंद्र के संबंध में लगभग दर्पण सममित है। ये सभी घटनाएं कम आवृत्तियों पर विशेष रूप से मजबूत हैं, जो हमारे लिए कोडिंग में महत्वपूर्ण हैं। यह भी बुरा है क्योंकि संकुचित छवि पर ब्लॉकों की सीमाएं ध्यान देने योग्य होंगी। मैं एन = 8 के साथ डीएफटी आधार को चित्रित करूंगा। पहली 2 पंक्तियाँ कोसाइन घटक हैं, अंतिम साइनस घटक हैं:

बढ़ती आवृत्ति के साथ डुप्लिकेट घटकों की उपस्थिति पर ध्यान दें।

आप मानसिक रूप से सोच सकते हैं कि एक सिग्नल कैसे विघटित हो सकता है, जिनमें से मूल्य धीरे-धीरे अधिकतम मूल्य से शुरू में कम से कम अंत में कम हो जाते हैं। अधिक या कम पर्याप्त सन्निकटन केवल अंत तक हार्मोनिक्स को करीब ला सकता है, जो हमारे लिए बहुत स्वस्थ नहीं है। बाईं ओर आकृति में, एकल-समाप्त सिग्नल का अनुमान। सममित - सममित:

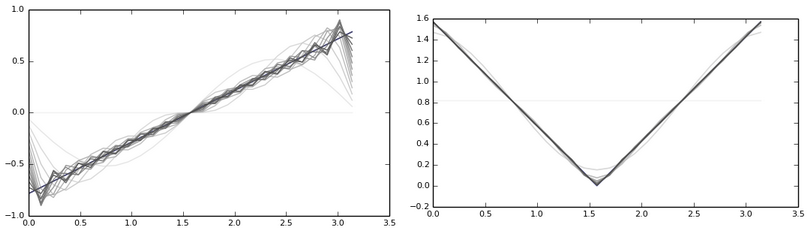
पहले के साथ, चीजें बेहद खराब हैं।
तो यह DCT के रूप में किया जा सकता है - 2 या किसी अन्य संख्या से आवृत्तियों को कम करने के लिए, ताकि कुछ दोलनों की संख्या आंशिक हो और सीमाएं अलग-अलग चरणों में हों? फिर घटक गैर-ऑर्थोगोनल होंगे। और कुछ भी नहीं करना है।

डीएसटी

यदि डीसीटी में कोजाइन के बजाय साइन का उपयोग किया जाता है तो क्या होगा? हमें असतत साइन ट्रांसफ़ॉर्म (DST) मिलता है। लेकिन हमारे कार्य के लिए वे सभी निर्बाध हैं, क्योंकि सीमाओं के दौरान सीन्स के पूरे और आधे हिस्से शून्य के करीब हैं। यही है, हमें डीएफटी के रूप में उसी अनुचित अपघटन के बारे में मिलता है।

DCT पर लौटना

वह सीमाओं पर कैसे कर रहा है? सब ठीक है। एंटीफेज और कोई शून्य नहीं हैं।

शेष सभी

गैर-फूरियर रूपांतरण। मैं वर्णन नहीं करूंगा।
WHT - मैट्रिक्स में मान -1 और 1 के साथ केवल चरण घटक होते हैं।
हार - अंशकालिक ऑर्थोगोनल तरंगिका रूपांतरित।
वे डीसीटी से नीच हैं, लेकिन गणना करना आसान है।

तो, सोचा था कि आप अपने स्वयं के परिवर्तन के साथ आने के लिए। इसे याद रखें:

1. आधार ऑर्थोगोनल होना चाहिए।
2. एक निश्चित आधार के साथ, आप संपीड़न गुणवत्ता में KLT को हरा नहीं सकते। इस बीच, वास्तविक तस्वीरों में, डीसीटी लगभग अवर है।
3. DFT और DST के लिए, सीमाओं को याद रखें।
4. और याद रखें कि डीसीटी का एक और अच्छा फायदा है - उनके घटक डेरिवेटिव की सीमाओं के पास, वे शून्य के बराबर हैं, जिसका अर्थ है कि पड़ोसी ब्लॉकों के बीच संक्रमण काफी सुचारू होगा।
5. माथे की संगणना के विपरीत: फूरियर ट्रांसफॉर्म में जटिलता ओ (एन * लॉगएन) के साथ तेज एल्गोरिदम होते हैं: ओ (एन ² )।

यह आसान नहीं होगा, है ना? हालाँकि, कुछ प्रकार की छवियों के लिए आप DCT से बेहतर आधार चुन सकते हैं।

यह खंड एक असतत कोसाइन ट्रांसफॉर्म विज्ञापन के समान निकला। लेकिन यह वास्तव में अच्छा है!

दो आयामी परिवर्तन

अब ऐसे प्रयोग करने की कोशिश करते हैं। उदाहरण के लिए, चित्र का एक टुकड़ा लें।

उनका 3D ग्राफ:

प्रत्येक पंक्ति पर DCT (N = 32) से गुजरते हैं:

अब मैं चाहता हूं कि आप प्राप्त गुणांक के प्रत्येक स्तंभ के माध्यम से अपनी आँखें चलाएं, अर्थात ऊपर से नीचे तक। याद रखें कि हमारा लक्ष्य महत्वहीन लोगों को हटाते हुए कुछ मूल्यों को छोड़ना है। निश्चित रूप से आपने अनुमान लगाया कि प्राप्त गुणांक के प्रत्येक स्तंभ के मूल्यों को मूल छवि के मूल्यों के समान ही विघटित किया जा सकता है। कोई भी हमें ऑर्थोगोनल परिवर्तन मैट्रिक्स को चुनने में प्रतिबंधित नहीं करता है, लेकिन हम इसे डीसीटी (एन = 8) का उपयोग करके फिर से करेंगे:

गुणांक (0,0) बहुत बड़ा निकला, इसलिए ग्राफ पर यह 4 गुना कम हो गया है।
तो क्या हुआ?
ऊपरी बाएं कोने सबसे महत्वपूर्ण गुणांक के सबसे महत्वपूर्ण अपघटन गुणांक हैं।
निचले बाएं कोने सबसे महत्वपूर्ण गुणांक के सबसे नगण्य अपघटन गुणांक हैं।
ऊपरी दाएं कोने सबसे महत्वहीन गुणांक के सबसे महत्वपूर्ण अपघटन गुणांक हैं।
निचला दायां कोना सबसे नगण्य गुणांक के सबसे नगण्य अपघटन गुणांक है।
यह स्पष्ट है कि गुणांक का महत्व कम हो जाता है अगर हम ऊपरी बाएँ से निचले दाईं ओर तिरछे चलते हैं। और जो अधिक महत्वपूर्ण है: (0, 7) या (7, 0)? उनका क्या मतलब है?
सबसे पहले, पंक्तियों द्वारा: ए ₀ = (ईएक्स ^टी ) ^टी = एक्सई ^टी (ट्रांसपोज़्ड, चूंकि सूत्र ए = एक्स कॉलम के लिए है), फिर कॉलम द्वारा: ए = ईए ₀ = एक्सई ^टी। यदि आप ध्यान से गणना करते हैं, तो आपको सूत्र मिलता है:

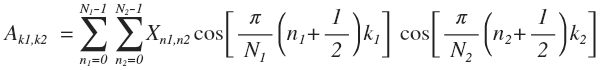
इस प्रकार, यदि वेक्टर को साइनसोइड में विघटित किया जाता है, तो मैट्रिक्स कॉस (अक्ष) * कॉस (द्वारा) के कार्यों में होता है। JPEG में प्रत्येक 8x8 ब्लॉक को फॉर्म के 64 कार्यों के रूप में दर्शाया गया है:

विकिपीडिया और अन्य स्रोतों में, ऐसे कार्यों को अधिक सुविधाजनक रूप में प्रस्तुत किया गया है:

इसलिए, गुणांक (0, 7) या (7, 0) समान रूप से उपयोगी हैं।
हालांकि, वास्तव में, यह 64 64-आयामी आधारों में सामान्य एक-आयामी अपघटन है। उपरोक्त सभी न केवल डीसीटी पर लागू होते हैं, बल्कि किसी भी रूढ़िवादी अपघटन पर भी लागू होते हैं। सादृश्य द्वारा कार्य करना, सामान्य मामले में हम एक एन-आयामी ऑर्थोगोनल परिवर्तन प्राप्त करते हैं।
और यहाँ एक 2-आयामी रैकून रूपांतरण (DCT 256x256) है। फिर से शून्य मानों के साथ। संख्या - सभी से गैर-शून्य गुणांक की संख्या (सबसे महत्वपूर्ण मूल्य जो ऊपरी बाएं कोने में त्रिकोणीय क्षेत्र में थे, छोड़ दिया गया था)।

याद रखें कि गुणांक (0, 0) को डीसी कहा जाता है, शेष 63 - एसी।

ब्लॉक आकार चयन

एक दोस्त पूछता है : जेपीईजी को विशेष रूप से 8x8 विभाजन के लिए क्यों इस्तेमाल किया जाता है? प्लस उत्तर से:

DCT ब्लॉक को मानता है जैसे कि यह आवधिक था और सीमाओं पर परिणामी कूद को फिर से बनाना पड़ता है। यदि आप 64x64 ब्लॉक लेते हैं, तो आपको सबसे अधिक संभावना है कि सीमाओं पर एक बड़ी छलांग होगी, और आपको संतोषजनक परिशुद्धता के लिए पुनर्निर्माण के लिए उच्च आवृत्ति वाले घटकों की बहुत आवश्यकता होगी।

जैसे, डीसीटी केवल आवधिक कार्यों पर अच्छी तरह से काम करता है, और यदि आप बड़े आकार लेते हैं, तो सबसे अधिक संभावना है कि आपको ब्लॉक की सीमाओं पर एक विशाल छलांग मिलेगी और इसे कवर करने के लिए आपको उच्च आवृत्ति वाले घटकों की बहुत आवश्यकता होगी। यह गलत है! यह स्पष्टीकरण डीएफटी के समान है, लेकिन डीसीटी के लिए नहीं, क्योंकि यह पूरी तरह से पहले घटकों के साथ ऐसी छलांग को कवर करता है।
बड़े खंडों के खिलाफ मुख्य तर्क के साथ एक ही पृष्ठ MPEG FAQ से उत्तर प्रदान करता है:

• बड़े ब्लॉक में तोड़ते समय थोड़ा लाभ।
• कम्प्यूटेशनल जटिलता में वृद्धि।
• एक ब्लॉक में बड़ी संख्या में तेज सीमाओं की उच्च संभावना, जो गिब्स प्रभाव का कारण बनेगी।

मैं अपने दम पर इस पर शोध करने का प्रस्ताव करता हूं। पहले वाले से शुरू करते हैं।

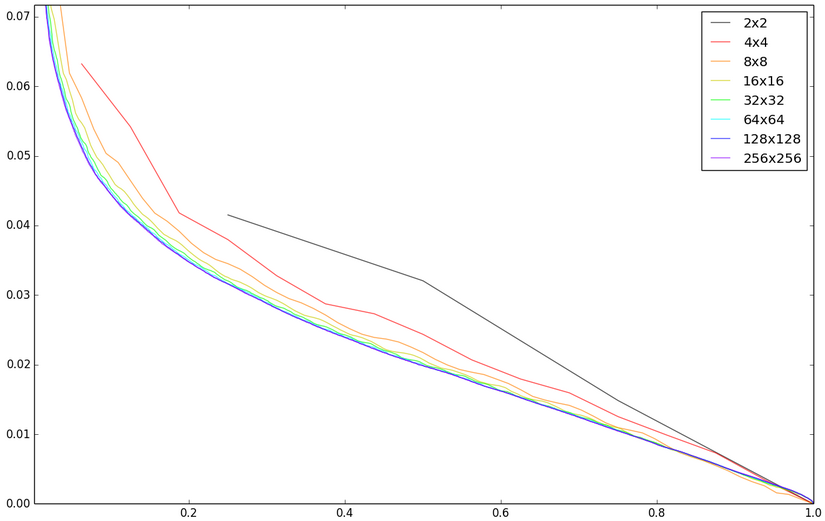
क्षैतिज अक्ष पहले गैर-शून्य गुणांक का अंश है। कार्यक्षेत्र - मूल से पिक्सेल का मानक विचलन। अधिकतम संभव विचलन एक इकाई के रूप में लिया जाता है। बेशक, एक तस्वीर स्पष्ट रूप से फैसले के लिए पर्याप्त नहीं है। इसके अलावा, मैं सही अभिनय नहीं कर रहा हूं, बस शून्यकरण कर रहा हूं। वास्तविक जेपीईजी में, परिमाणीकरण मैट्रिक्स के आधार पर, उच्च आवृत्ति वाले घटकों के केवल छोटे मूल्य रीसेट किए जाते हैं। इसलिए, निम्न प्रयोगों और निष्कर्षों को सिद्धांतों और पैटर्न की सतही पहचान के लिए डिज़ाइन किया गया है।
आप विभिन्‍न ब्लॉकों में विभिन्‍न 25 प्रतिशत गुणांक के मरीजों (बाएं से दाएं, फिर दाएं से बाएं) से तुलना कर सकते हैं:


बड़े ब्लॉकों को नहीं दिखाया गया है, जैसा कि 32x32 से नेत्रहीन लगभग अप्रभेद्य है। अब आइए मूल छवि के साथ पूर्ण अंतर को देखें (2 बार प्रवर्धित, अन्यथा वास्तव में कुछ भी दिखाई नहीं देता है):


8x8 4x4 की तुलना में बेहतर परिणाम देता है। आकार में और वृद्धि अब एक अलग लाभ प्रदान नहीं करती है। हालाँकि, मैं 8x8 के बजाय 16x16 के बारे में गंभीरता से सोचूंगा: 33% की जटिलता (अगले पैराग्राफ में जटिलता के बारे में) में वृद्धि, एक ही संख्या में कारकों के साथ एक छोटा, लेकिन फिर भी दृश्यमान सुधार देती है। हालांकि, 8x8 का विकल्प काफी उचित लगता है और, शायद, सुनहरे मतलब है। JPEG को 1991 में प्रकाशित किया गया था। मुझे लगता है कि उस समय के प्रोसेसर के लिए इस तरह की संपीड़न बहुत मुश्किल थी।

दूसरा तर्क। यह याद रखना चाहिए कि जैसे-जैसे ब्लॉक आकार बढ़ता है, अधिक गणना की आवश्यकता होगी। कितना अनुमान लगाते हैं। माथे पर रूपांतरण की जटिलता, जैसा कि हम पहले से ही जानते हैं: ओ (एन ² ), क्योंकि प्रत्येक गुणांक में एन शब्द शामिल हैं। लेकिन व्यवहार में, एक प्रभावी फास्ट फूरियर ट्रांसफॉर्म एल्गोरिथ्म (एफएफटी, फास्ट फूरियर ट्रांसफॉर्म, एफएफटी) का उपयोग किया जाता है। उनका विवरण लेख के दायरे से परे है। इसकी जटिलता: O (N * logN)। द्वि-आयामी अपघटन के लिए, आपको इसे दो बार एन बार उपयोग करने की आवश्यकता है। इस प्रकार, 2D DCT की जटिलता O (N ² logN) है। अब एक ब्लॉक और कई छोटे लोगों के साथ छवि की जटिलता की तुलना करें:

• एक ब्लॉक (kN) x (kN): O ((kN) ² लॉग (kN)) = O (k ² N ² लॉग (kN))
• k * k ब्लॉक N * N: O (k ² N ² logN)

इसका मतलब यह है कि, उदाहरण के लिए, जब 64x64 में तोड़ना गणना 8x8 से दो गुना अधिक कठिन है।

तीसरा तर्क। यदि हमारे पास छवि में रंगों की एक तेज सीमा है, तो यह पूरे ब्लॉक को प्रभावित करेगा। शायद यह बेहतर होगा यदि यह ब्लॉक काफी छोटा है, क्योंकि कई पड़ोसी ब्लॉकों में, ऐसी सीमा शायद अब नहीं होगी। हालाँकि, सीमाओं से दूर, क्षीणन जल्दी होता है। इसके अलावा, सीमा खुद बेहतर दिखेगी। आइए एक उदाहरण पर बड़ी संख्या में विपरीत बदलावों के साथ फिर से जांचते हैं, केवल एक चौथाई गुणांक के साथ:

यद्यपि 16x16 ब्लॉकों की विकृति 8x8 की तुलना में आगे बढ़ती है, फिर भी शिलालेख चिकना है। इसलिए, केवल पहले दो तर्कों ने मुझे आश्वस्त किया। लेकिन मुझे कुछ और 16x16 का विभाजन पसंद है।

परिमाणीकरण

इस स्तर पर, हमारे पास कोसाइन रूपांतरण गुणांक वाले 8x8 मैट्रिसेस का एक गुच्छा है। नगण्य गुणांक से छुटकारा पाने का समय आ गया है। नवीनतम ऑड्स को शून्य करने की तुलना में अधिक सुरुचिपूर्ण समाधान है, जैसा कि हमने ऊपर किया था। हम इस पद्धति से खुश नहीं हैं, क्योंकि गैर-शून्य मान अत्यधिक सटीकता के साथ संग्रहीत होते हैं, और जो लोग अशुभ थे, उनमें से कुछ महत्वपूर्ण हो सकते हैं। आउटपुट - आपको मात्राकरण मैट्रिक्स का उपयोग करने की आवश्यकता है। इस स्तर पर नुकसान ठीक होता है। प्रत्येक फूरियर गुणांक को परिमाणीकरण मैट्रिक्स में संबंधित संख्या से विभाजित किया जाता है। एक उदाहरण पर विचार करें। हमारे एक प्रकार का जानवर से पहले ब्लॉक ले लो और यों। JPEG विनिर्देशन एक मानक मैट्रिक्स प्रदान करता है:

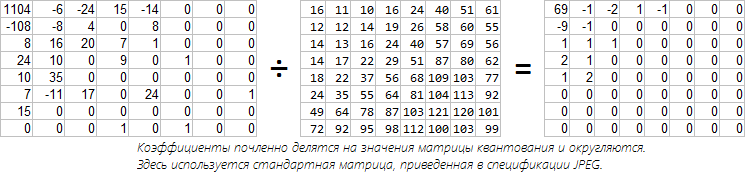
स्टैंडर्ड मैट्रिक्स फास्टस्टोन और इरफानव्यू में 50% गुणवत्ता से मेल खाती है। गुणवत्ता और संपीड़न अनुपात के संतुलन के संदर्भ में ऐसी तालिका का चयन किया गया था। मुझे लगता है कि डीसी गुणांक के लिए मूल्य इस तथ्य के कारण पड़ोसी की तुलना में बड़ा है कि डीसीटी सामान्यीकृत नहीं है और पहले मूल्य को जितना चाहिए उससे अधिक प्राप्त किया जाता है। उच्च-आवृत्ति गुणांक उनके कम महत्व के कारण अधिक मोटे हो जाते हैं। मुझे लगता है कि अब इस तरह के मैट्रिस का उपयोग शायद ही कभी किया जाता है, क्योंकि गुणवत्ता में गिरावट स्पष्ट रूप से ध्यान देने योग्य है। कोई भी आपकी अपनी तालिका का उपयोग करने से मना करता है (मान 1 से 255 तक)
जब डिकोडिंग किया जाता है, तो रिवर्स प्रक्रिया होती है - मात्रात्मक गुणांक को मात्रात्मक मैट्रिक्स के मूल्यों द्वारा शब्द से गुणा किया जाता है। लेकिन जब से हमने मानों को गोल किया, हम मूल फूरियर गुणांक को ठीक से पुनर्स्थापित नहीं कर पाएंगे। परिमाणीकरण संख्या जितनी बड़ी होगी, त्रुटि उतनी ही अधिक होगी। इस प्रकार, पुनर्निर्मित गुणांक केवल निकटतम गुणक है।
एक और उदाहरण:


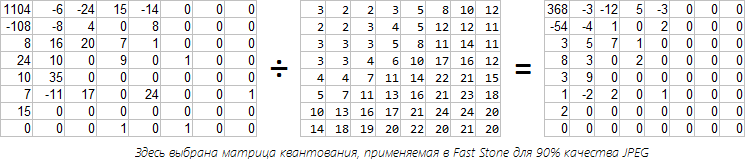
और मिठाई के लिए, 5% (फास्ट स्टोन में कोडिंग) की गुणवत्ता पर विचार करें।

इस ब्लॉक को पुनर्स्थापित करते समय, हमें केवल औसत मूल्य प्लस ऊर्ध्वाधर ढाल (-1 के संरक्षित मूल्य के कारण) मिलता है। लेकिन उसके लिए, केवल दो मूल्य संग्रहीत हैं: 7 और -1। अन्य ब्लॉकों के साथ, स्थिति बेहतर नहीं है, यहां बहाल छवि है:


वैसे, लगभग 100% गुणवत्ता। जैसा कि आप सोच सकते हैं, इस मामले में, परिमाणीकरण मैट्रिक्स में पूरी तरह से इकाइयां शामिल हैं, अर्थात, परिमाणीकरण नहीं होता है। हालाँकि, पूर्णांक में गुणांक के गोलाई के कारण, हम मूल छवि को ठीक नहीं कर सकते हैं। उदाहरण के लिए, एक रैकून ने पिक्सल्स का 96% सही ढंग से बनाए रखा, और 4% 1/256 से भिन्न हुआ। बेशक, ऐसे "विकृतियों" को दृष्टिगत रूप से नहीं देखा जा सकता है।
और यहां आप विभिन्न कैमरों के परिमाणीकरण मैट्रिक्स देख सकते हैं।

कोडिंग

आगे बढ़ने से पहले, हमें यह समझने की आवश्यकता है कि सरल उदाहरणों का उपयोग करके प्राप्त मूल्यों को कैसे संकुचित किया जाए।

उदाहरण 0 (वार्मिंग के लिए)
ऐसी स्थिति की कल्पना करें जहां आपका दोस्त एक सूची के साथ आपके घर में एक पत्रक को भूल गया था और अब आपसे फोन द्वारा इसे निर्देशित करने के लिए कहता है (संचार के अन्य तरीके नहीं हैं)।
सूची:

• d9rg3
• wfr43gt
• wfr43gt
• d9rg3
• d9rg3
• d9rg3
• wfr43gt
• d9rg3

आप अपने काम को कैसे आसान करेंगे? आपको इन सभी शब्दों को दर्दनाक रूप से निर्देशित करने की कोई विशेष इच्छा नहीं है। लेकिन उनमें से केवल दो हैं और उन्हें दोहराया जाता है। इसलिए, आप किसी तरह पहले दो शब्दों को निर्धारित करते हैं और सहमत होते हैं कि आगे "d9rg3" को पहला शब्द कहा जाएगा, और "wfr43gt" - दूसरा। फिर यह तय करने के लिए पर्याप्त होगा: 1, 2, 2, 1, 1, 1, 2, 1।

हम इसी तरह के शब्दों को ए, बी, सी ... और उन्हें प्रतीक कहते हैं। और प्रतीक के तहत, कुछ भी छिपाया जा सकता है: एक चिड़ियाघर में वर्णमाला का एक अक्षर, एक शब्द या दरियाई घोड़ा। मुख्य बात यह है कि समान अवधारणाएं समान अवधारणाओं के अनुरूप हैं, और अलग - अलग। चूंकि हमारा कार्य कुशल कोडिंग (संपीड़न) है, हम बिट्स के साथ काम करेंगे, क्योंकि ये सूचना प्रतिनिधित्व की सबसे छोटी इकाइयां हैं। इसलिए, हम सूची को ABBAAABA के रूप में लिखते हैं। "पहले शब्द" और "दूसरे शब्द" के बजाय, बिट्स 0 और 1 का उपयोग किया जा सकता है। फिर ABBAAABA को 01100010 (8 बिट्स = 1 बाइट) के रूप में एन्कोड किया गया है।


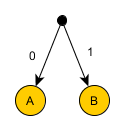उदाहरण 1
एबीसी सांकेतिक शब्दों में बदलना।
3 अलग-अलग वर्ण (A, B, C) 2 संभावित बिट मानों (0 और 1) के साथ मेल नहीं खा सकते हैं। और यदि ऐसा है, तो आप प्रति वर्ण 2 बिट का उपयोग कर सकते हैं। उदाहरण के लिए:

• A: 00
• B: 01
• C: 10

एक प्रतीक के साथ जुड़े बिट्स के एक अनुक्रम को एक कोड कहा जाएगा। ABC को एनकोड किया जाएगा: 000110


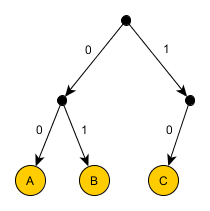उदाहरण 2
AAAAAABC को एनकोड करें।
प्रति वर्ण 2 बिट का उपयोग करना थोड़ा बेकार लगता है। यदि आप इस तरह की कोशिश करते हैं:

• A: 0
• बी: १
• C: 00

कोडेड अनुक्रम: 000000100
जाहिर है, यह विकल्प उपयुक्त नहीं है, क्योंकि यह स्पष्ट नहीं है कि इस अनुक्रम के पहले दो बिट्स को कैसे डीकोड किया जाए: एए या सी की तरह? कोड के बीच किसी भी विभाजक का उपयोग करना बहुत ही बेकार है, हम सोचेंगे कि इस बाधा को अलग तरीके से कैसे कम किया जाए। तो, विफलता इसलिए हुई क्योंकि C कोड A से शुरू होता है, लेकिन हम A को एक बिट से एन्कोड करने के लिए दृढ़ हैं, भले ही B और C दो प्रत्येक हों। इस तरह की इच्छा के आधार पर, A कोड देगा 0. फिर कोड B और C 0. पर शुरू नहीं हो सकते हैं, लेकिन वे 1 पर कर सकते हैं:

• A: 0
• B: 10
• C: 11

अनुक्रम को इनकोड किया गया है: 0000001011। मानसिक रूप से इसे डिकोड करने का प्रयास करें। आप इसे केवल एक ही तरीके से कर सकते हैं।
हमने दो कोडिंग आवश्यकताएं विकसित की हैं:

1. वर्ण का वजन जितना अधिक होगा, उतना ही कम कोड होना चाहिए। और इसके विपरीत।
2. अस्पष्ट डिकोडिंग के लिए, एक चरित्र कोड किसी अन्य वर्ण के लिए एक कोड के साथ शुरू नहीं हो सकता है।

जाहिर है, पात्रों का क्रम महत्वपूर्ण नहीं है, हम केवल उनकी घटना की आवृत्ति में रुचि रखते हैं। इसलिए, प्रत्येक प्रतीक एक निश्चित संख्या से जुड़ा होता है जिसे वजन कहा जाता है। एक प्रतीक का वजन या तो एक सापेक्ष मूल्य हो सकता है, इसकी घटना के अनुपात को दर्शाता है, या पूर्ण, वर्णों की संख्या के बराबर। मुख्य बात यह है कि वजन पात्रों की घटना के आनुपातिक हैं।

उदाहरण 3
किसी भी भार के साथ 4 वर्णों के लिए सामान्य मामले पर विचार करें।

• A: पा
• बी: पीबी
• सी: पीसी
• डी: पीडी

व्यापकता के नुकसान के बिना, हम पा ≥ pb ≥ pc। Pd सेट करते हैं। केवल दो विकल्प हैं जो लंबाई में मूलभूत रूप से भिन्न हैं:

कौन सा बेहतर है? ऐसा करने के लिए, एन्कोड किए गए संदेशों की प्राप्त लंबाई की गणना करें:
डब्ल्यू 1 = 2 * पा + 2 * पीबी + 2 * पीसी + 2 * पीडी
डब्ल्यू 2 = पा + 2 * पीबी + 3 * पीसी + 3 * पीडी
यदि W1 W2 (W1-W2 <0) से कम है, तो पहले विकल्प का उपयोग करना बेहतर है:
डब्ल्यू 1-डब्ल्यू 2 = पा - (पीसी + पीडी) <0 => पा <पीसी + पीडी।
यदि सी और डी एक साथ दूसरों की तुलना में अधिक बार होते हैं, तो उनके सामान्य शीर्ष को एक बिट से सबसे छोटा कोड मिलता है। अन्यथा, एक बिट चरित्र ए के पास जाता है। इसलिए, पात्रों का संयोजन एक स्वतंत्र चरित्र के रूप में व्यवहार करता है और आने वाले पात्रों के योग के बराबर वजन होता है।
सामान्य तौर पर, यदि p किसी वर्ण के भार को उसकी घटना के एक अंश (0 से 1 तक) का प्रतिनिधित्व करता है, तो सबसे अच्छी कोड लंबाई s = -log ₂ p है।
एक साधारण मामले में इस पर विचार करें (पेड़ के रूप में इसकी कल्पना करना आसान है)। तो, आपको 2 ^एस अक्षर को समान भार (1/2 ^एस ) के साथ एन्कोड करना होगा। भार की समानता के कारण, कोड की लंबाई समान होगी। प्रत्येक पात्र को बिट्स की आवश्यकता होगी। तो, यदि प्रतीक का वजन 1/2 ^{s है} , तो इसकी लंबाई s है। यदि हम वजन को p से बदलते हैं, तो हमें कोड की लंबाई s = -log ₂ p मिलती है। इसलिए, यदि एक वर्ण दूसरे की तुलना में दो बार कम होता है, तो उसके कोड की लंबाई थोड़ी लंबी होगी। हालांकि, ऐसा निष्कर्ष बनाना आसान है यदि आपको याद है कि एक बिट जोड़ने से आप संभावित विकल्पों की संख्या को दोगुना कर सकते हैं।
और एक और अवलोकन - सबसे छोटे वज़न वाले दो अक्षर हमेशा सबसे बड़े, लेकिन समान कोड लंबाई वाले होते हैं। इसके अलावा, उनके बिट्स, आखिरी मैच को छोड़कर। यदि यह सच नहीं था, तो उपसर्ग का उल्लंघन किए बिना कम से कम एक कोड को 1 बिट से छोटा किया जा सकता है। इसका अर्थ है कि कोड ट्री में सबसे छोटे वज़न वाले दो वर्णों का एक समान मूल स्तर होता है। आप इसे ऊपर C और D के साथ देख सकते हैं।

उदाहरण 4
आइए, पिछले उदाहरण में प्राप्त निष्कर्षों के आधार पर, निम्न उदाहरण को हल करने का प्रयास करें।

1. सभी पात्रों को वजन द्वारा अवरोही क्रम में क्रमबद्ध किया जाता है।
2. अंतिम दो वर्णों को एक समूह में जोड़ा जाता है। इस समूह को इन तत्वों के भार के योग के बराबर भार सौंपा गया है। यह समूह प्रतीकों और अन्य समूहों के साथ एल्गोरिथ्म में भाग लेता है।

केवल एक समूह के रहने तक चरण दोहराए जाते हैं। प्रत्येक समूह में, एक वर्ण (या उपसमूह) को बिट 0 और दूसरे को 1 बिट सौंपा गया है।
इस एल्गोरिथ्म को हफ़मैन कोडिंग कहा जाता है।
चित्रण 5 वर्णों (A: 8, B: 6, C: 5, D: 4, E: 3) के साथ एक उदाहरण दिखाता है। प्रतीक का वजन (या समूह) दाईं ओर इंगित किया गया है।

हम गुणांक को कोड करते हैं

लौट आओ। अब हमारे पास प्रत्येक में 64 गुणांक वाले कई ब्लॉक हैं, जिन्हें किसी तरह संरक्षित करने की आवश्यकता है। सबसे सरल उपाय प्रति गुणांक की निश्चित संख्या का उपयोग करना है - जाहिर है असफल। हम सभी प्राप्त मूल्यों (जैसे, उनके मूल्य पर गुणांक की संख्या की निर्भरता) का एक हिस्टोग्राम का निर्माण करते हैं:

कृपया ध्यान दें - पैमाना लघुगणक है!क्या आप 200 से अधिक मूल्यों के संचय का कारण बता सकते हैं? ये डीसी गुणांक हैं। चूंकि वे बाकी हिस्सों से बहुत अलग हैं, इसलिए यह आश्चर्यजनक नहीं है कि वे अलग-अलग एन्कोडेड हैं। यहाँ सिर्फ डीसी हैं:

कृपया ध्यान दें कि ग्राफ़ का आकार जोड़े और पिक्सेल के जोड़े में विभाजित करने के शुरुआती प्रयोगों से मिलता-जुलता है।
सामान्य तौर पर, डीसी गुणांक के मान 0 से 2047 तक भिन्न हो सकते हैं (अधिक सटीक रूप से -1024 से 1023 तक, क्योंकि जेपीईजी में सभी मूल मूल्यों से 128 घटाया गया है। , जो डीसी से 1024 घटाव से मेल खाती है) और छोटी चोटियों के साथ समान रूप से समान रूप से वितरित किया जाता है। इसलिए, हफ़मैन कोडिंग यहां बहुत मदद नहीं करेगा। और कल्पना करें कि कोडिंग पेड़ कितना बड़ा होगा! और डिकोडिंग के दौरान, आपको इसमें मूल्यों की तलाश करनी होगी। यह बहुत महंगा है। हम आगे सोचते हैं।
डीसी-गुणांक 8x8 ब्लॉक का औसत मूल्य है। एक ढाल संक्रमण की कल्पना करें (यद्यपि संपूर्ण नहीं), जो अक्सर तस्वीरों में पाया जाता है। डीसी मान स्वयं अलग होंगे, लेकिन वे एक अंकगणितीय प्रगति का प्रतिनिधित्व करेंगे। इसलिए, उनका अंतर कम या ज्यादा स्थिर रहेगा। आइए मतभेदों का एक हिस्टोग्राम बनाएं:

यह पहले से ही बेहतर है, क्योंकि मूल्य, सामान्य रूप से, शून्य के पास केंद्रित हैं (लेकिन हफ़मैन एल्गोरिथ्म फिर से बहुत बड़ा पेड़ देगा)। छोटे मूल्य (पूर्ण मूल्य में) आम हैं, बड़े दुर्लभ हैं। और चूंकि छोटे मान छोटे बिट्स लेते हैं (यदि आप अग्रणी शून्य हटाते हैं), तो संपीड़न नियमों में से एक को अच्छी तरह से निष्पादित किया जाता है: बड़े वजन वाले शॉर्ट कोड (और इसके विपरीत) कोड असाइन करें। अब तक, हम एक और नियम की विफलता से सीमित हैं: असंदिग्ध डिकोडिंग की असंभवता। सामान्य तौर पर, इस समस्या को निम्नलिखित तरीकों से हल किया जा सकता है: विभाजक कोड के साथ भ्रमित हो जाएं, कोड की लंबाई इंगित करें, उपसर्ग कोड का उपयोग करें (आप पहले से ही उन्हें जानते हैं - यह मामला है जब कोई कोड दूसरे से शुरू नहीं होता है)। आइए सरल दूसरे विकल्प से जाएं, अर्थात्, प्रत्येक गुणांक (अधिक सटीक रूप से, पड़ोसी के बीच का अंतर) इस तरह लिखा जाएगा: (लंबाई) (मान),ऐसी प्लेट पर:

यही है, सकारात्मक मूल्यों को सीधे उनके द्विआधारी प्रतिनिधित्व द्वारा एन्कोड किया गया है, और नकारात्मक मानों को सीधे एनकोड किया गया है, लेकिन प्रमुख 1 द्वारा प्रतिस्थापित 0. के साथ यह तय करना बाकी है कि लंबाई को कैसे एन्कोड किया जाए। चूंकि 12 संभावित मान हैं, इसलिए लंबाई को संग्रहीत करने के लिए 4 बिट्स का उपयोग किया जा सकता है। लेकिन यहां हफ़मैन कोडिंग का उपयोग करना बेहतर है।

लंबाई 4 और 6 वाले मान सबसे अधिक हैं, इसलिए उन्हें सबसे छोटा कोड (00 और 01) मिला।

जेपीईजी में कार्यान्वयन की विशेषताएं:
सवाल उठ सकता है: क्यों, उदाहरण के लिए, मूल्य 9 में कोड 1111110 है, न कि 1111111? आखिरकार, आप "0" के बगल में "9" को उच्च स्तर तक सुरक्षित रूप से बढ़ा सकते हैं? तथ्य यह है कि जेपीईजी में आप केवल इकाइयों से युक्त कोड का उपयोग नहीं कर सकते हैं - ऐसा कोड आरक्षित है।
एक और विशेषता है। वर्णित हफ़मैन एल्गोरिथ्म द्वारा प्राप्त कोड जेपीईजी में कोड के साथ थोड़ा भी मेल नहीं खा सकते हैं, हालांकि उनकी लंबाई समान होगी। हफ़मैन एल्गोरिथ्म का उपयोग करते हुए, वे कोड की लंबाई प्राप्त करते हैं, और कोड स्वयं उत्पन्न होते हैं (एल्गोरिथ्म सरल है - छोटे कोड के साथ शुरू करें और उन्हें पेड़ के बदले में संभव के रूप में बाईं ओर जोड़ दें, उपसर्ग संपत्ति का संरक्षण)। उदाहरण के लिए, सूची के ऊपर के पेड़ को संग्रहीत किया जाता है: 0,2,3,1,1,1,1,1,1। और, ज़ाहिर है, मूल्यों की एक सूची संग्रहीत है: 4,6,3,5,7,2,8,8,1,0,9। डिकोडिंग करते समय, कोड उसी तरह से उत्पन्न होते हैं।

अब आदेश। हमने पता लगाया कि डीसी कैसे संग्रहीत किए जाते हैं:
[डीसी की लंबाई के लिए हफ़मैन कोड _{भिन्न} (बिट्स)] [डीसी _{भिन्न} ]
जहां डीसी _{भिन्न} = डीसी _{वर्तमान} - डीसी _{पिछला}

हम एसी को देखते हैं:

चूंकि ग्राफ डीसी अंतर के लिए ग्राफ के समान है, सिद्धांत समान है: [एसी लंबाई के लिए हफमैन कोड (बिट्स में)] [एसी]। लेकिन वास्तव में नहीं! चूँकि ग्राफ़ पर पैमाना लॉगरिदमिक है, यह तुरंत ध्यान देने योग्य नहीं है कि आवृत्ति में 2 की तुलना में लगभग 10 गुना अधिक शून्य मान हैं। यह समझ में आता है - सभी लोग परिमाणीकरण से नहीं बचे। आइए हम परिमाणीकरण चरण (फास्टस्टोन परिमाणीकरण मैट्रिक्स, 90% का उपयोग करके) में प्राप्त मूल्यों के मैट्रिक्स पर लौटें।

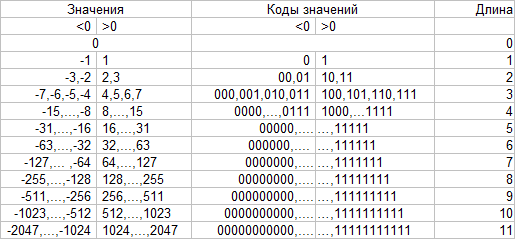
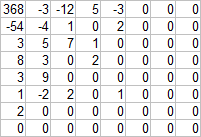चूंकि लगातार शून्य के कई समूह हैं, इसलिए विचार केवल समूह में शून्य की संख्या दर्ज करने का है। इस संपीड़न एल्गोरिदम को RLE (रन-लेंथ एन्कोडिंग) कहा जाता है। यह "लगातार आने वाले" दौर की दिशा का पता लगाने के लिए रहता है - कौन किसका अनुसरण करता है? बाएं से दाएं और ऊपर से नीचे तक लिखना बहुत प्रभावी नहीं है, क्योंकि नॉनजेरो गुणांक ऊपरी बाएं कोने के पास केंद्रित है, और निचले दाएं कोने के करीब, अधिक शून्य है।

इसलिए, जेपीईजी में "ज़िग-ज़ैग" नामक एक आदेश का उपयोग किया जाता है, इसे बाएं आकृति में दिखाया गया है। यह विधि शून्य के समूहों को अच्छी तरह से अलग करती है। सही आंकड़े में - वैकल्पिक वैकल्पिक हल, जेपीईजी से संबंधित नहीं, बल्कि एक जिज्ञासु नाम ( प्रमाण ) के साथ। इंटरलेप किए गए वीडियो को कंप्रेस करते समय इसका उपयोग एमपीईजी में किया जा सकता है। बाईपास एल्गोरिदम की पसंद छवि की गुणवत्ता को प्रभावित नहीं करती है, लेकिन शून्य के एन्कोडेड समूहों की संख्या को बढ़ा सकती है, जो अंततः फ़ाइल आकार को प्रभावित कर सकती है।
हम अपने रिकॉर्ड को संशोधित करते हैं। प्रत्येक गैर-शून्य एसी गुणांक के लिए:
[एसी से पहले शून्य की संख्या] [एसी लंबाई के लिए हफ़मैन कोड (बिट्स में)] [एसी]
मुझे लगता है कि आप तुरंत कहेंगे - शून्य की संख्या भी हफमैन द्वारा पूरी तरह से एन्कोडेड है! यह बहुत करीबी और अच्छा जवाब है। लेकिन आप थोड़ा अनुकूलन कर सकते हैं। कल्पना करें कि हमारे पास कुछ एसी गुणांक हैं, जिसके पहले 7 शून्य थे (निश्चित रूप से, यदि आप एक शून्य तरीके से लिखते हैं)। ये शून्य मानों की भावना है जो मात्रा का सामना नहीं कर सके। सबसे अधिक संभावना है, हमारे गुणांक भी बुरी तरह से पस्त हो गए और यह छोटा हो गया, जिसका अर्थ है कि इसकी लंबाई कम है। इसलिए, एसी से पहले शून्य की संख्या और एसी की लंबाई निर्भर मूल्य हैं। इसलिए, वे इस प्रकार लिखते हैं:
[हफ़मैन कोड (एसी से पहले शून्य की संख्या, एसी की लंबाई (बिट्स में))] [एसी]
एन्कोडिंग एल्गोरिथ्म समान रहता है: उन जोड़े (एसी से पहले शून्य की संख्या, एसी की लंबाई) जो अक्सर छोटे कोड प्राप्त करेंगे और इसके विपरीत।

हम इन जोड़े और हफ़मैन पेड़ के लिए मात्रा की निर्भरता का एक हिस्टोग्राम का निर्माण करते हैं।

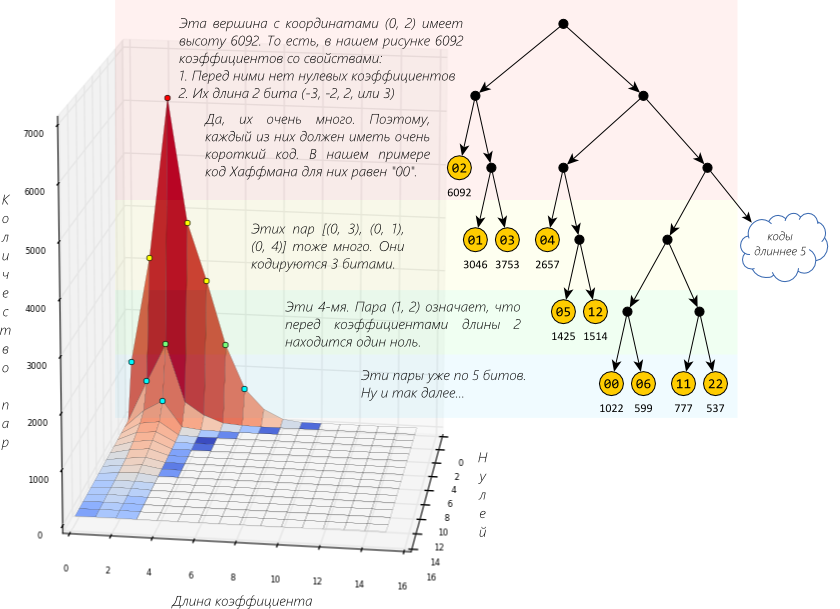लंबी "पर्वत श्रृंखला" हमारी धारणा की पुष्टि करती है।

जेपीईजी में कार्यान्वयन की विशेषताएं:
ऐसी जोड़ी 1 बाइट पर कब्जा करती है: शून्य की संख्या के लिए 4 बिट्स और एसी की लंबाई के लिए 4 बिट्स। 4 बिट्स 0 से 15. के मान हैं। एसी की लंबाई के लिए, पर्याप्त मात्रा में पर्याप्त है, लेकिन क्या 15 से अधिक शून्य हो सकते हैं? फिर अधिक जोड़े का उपयोग किया जाता है। उदाहरण के लिए, 20 शून्य के लिए: (15, 0) (5, एसी)। यही है, 16 वें शून्य को गैर-शून्य गुणांक के रूप में एन्कोड किया गया है। चूंकि ब्लॉक के अंत की ओर हमेशा बहुत शून्य होता है, अंतिम गैर-शून्य गुणांक के बाद एक जोड़ी (0,0) का उपयोग किया जाता है। इसे डीकोड साधन में मिलेंगे तो शेष मानों 0. हैं

यह पता चला कि प्रत्येक ब्लॉक इनकोडिंग एक फ़ाइल में संग्रहीत किया जाता है इस प्रकार है:
डीसी के लिए [Huffman कोड लंबाई _diff]
[डीसी _{भिन्न} ]
[हाफ़मैन कोड के लिए (एसी ₁ से पहले शून्य की संख्या , लंबाई एसी ₁ ]
[एसी ₁ ]
...
[हफ़मैन कोड के लिए (शून्य से पहले एसी _n , लंबाई एसी _{n की संख्या} ]
[एसी _n ]
जहां एसी _मैं नॉनजरो एसी गुणांक हैं।

रंग छवि

जिस तरह से एक रंग छवि प्रस्तुत की जाती है वह चयनित रंग मॉडल पर निर्भर करती है। एक सरल उपाय आरजीबी का उपयोग करना है और छवि के प्रत्येक रंग चैनल को व्यक्तिगत रूप से एन्कोड करना है। फिर एन्कोडिंग ग्रे छवि के एन्कोडिंग से अलग नहीं होगी, केवल 3 गुना अधिक काम। लेकिन छवि संपीड़न बढ़ाया जा सकता है यदि आपको याद है कि आंख रंग की तुलना में चमक में बदलाव के लिए अधिक संवेदनशील है। इसका मतलब है कि रंग को चमक की तुलना में अधिक नुकसान के साथ संग्रहीत किया जा सकता है। RGB में एक अलग luminance चैनल नहीं है। यह प्रत्येक चैनल के मूल्यों के योग पर निर्भर करता है। इसलिए, आरजीबी क्यूब (यह सभी संभावित मूल्यों का एक प्रतिनिधित्व है) विकर्ण पर बस "रखा" है - उच्च, उज्जवल। लेकिन वे इस तक सीमित नहीं हैं - क्यूब पक्षों से थोड़ा निचोड़ा हुआ है, और यह एक समानांतर रूप से निकला है, लेकिन यह केवल आंख की विशेषताओं को ध्यान में रखना है। उदाहरण के लिए, यह नीले रंग की तुलना में हरे रंग के लिए अधिक अतिसंवेदनशील है।तो YCbCr मॉडल दिखाई दिया।

(Intel.com से छवि)
Y luminance घटक है, Cb और Cr नीले और लाल रंग-अंतर घटक हैं। इसलिए, यदि वे छवि को अधिक दृढ़ता से संपीड़ित करना चाहते हैं, तो RGB को YCbCr में बदल दिया जाता है, और Cb और Cr चैनल को पतला कर दिया जाता है। यही है, वे छोटे खंडों में तोड़ते हैं, उदाहरण के लिए 2x2, 4x2, 1x2, और औसतन एक खंड के सभी मान। या, दूसरे शब्दों में, वे इस चैनल के लिए छवि का आकार 2 या 4 गुना कम करके और / या क्षैतिज रूप से घटाते हैं।

प्रत्येक 8x8 ब्लॉक एन्कोडेड है (DCT + Huffman), और इनकोडिंग क्रम इस क्रम में लिखे गए हैं:

यह उत्सुक है कि जेपीईजी विनिर्देश मॉडल की पसंद को सीमित नहीं करता है, अर्थात, एनकोडर कार्यान्वयन मनमाने ढंग से छवि को रंग घटकों (चैनलों) में विभाजित कर सकता है और प्रत्येक को अलग से सहेजा जाएगा। मैं ग्रेस्केल (1 चैनल), YCbCr (3), RGB (3), YCbCrK (4), CMYK (4) के उपयोग से अवगत हूं। पहले तीन को लगभग सभी का समर्थन प्राप्त है, लेकिन अंतिम 4-चैनल के साथ समस्याएं हैं। फास्टस्टोन, जीआईएमपी उन्हें सही तरीके से समर्थन करते हैं, और नियमित रूप से विंडोज, पेंट.नेट प्रोग्राम सभी जानकारी को सही ढंग से निकालते हैं, लेकिन फिर 4 ब्लैक चैनल को फेंक देते हैं, इसलिए ( एंटेले ने कहा कि उन्होंने इसे बाहर नहीं फेंका, उनकी टिप्पणियों को पढ़ें) एक हल्की छवि दिखाते हैं। बाईं ओर क्लासिक YCbCr JPEG है, दाईं ओर CMYK JPEG है:

यदि वे रंग में भिन्न हैं, या केवल एक तस्वीर दिखाई दे रही है, तो सबसे अधिक संभावना है कि आपके पास IE (कोई भी संस्करण) (UPD है। टिप्पणियों में "या सफारी" कहें)। आप विभिन्न ब्राउज़रों में लेख को खोलने का प्रयास कर सकते हैं।

और एक बात

अतिरिक्त सुविधाओं के बारे में संक्षेप में।

प्रगतिशील मोड

हम तालिकाओं के योग में परिणामी डीसीटी गुणांक तालिकाओं को घटाते हैं (जैसे (डीसी; -19, -22, 2, 1) = (डीसी, 0, 0, 0, 0) + (0, -20, -20, 0, 0) + (0, 1, -2, 2, 1))। सबसे पहले, हम सभी पहले शब्दों को एन्कोड करते हैं (जैसा कि हमने पहले ही सीखा है: हफ़मैन और ज़िगज़ैग ट्रैवर्सल), फिर दूसरा, आदि यह चाल धीमी इंटरनेट एक्सेस के लिए उपयोगी है, क्योंकि केवल डीसी गुणांक पहले से लोड किए जाते हैं, जो कि 8x8 पिक्सेल के साथ किसी न किसी चित्र का निर्माण करने के लिए उपयोग किया जाता है। फिर तस्वीर को निखारने के लिए AC गुणांकों को गोल किया। फिर उनके लिए सकल सुधार, फिर अधिक सटीक। अच्छी तरह से और इतने पर। गुणांक गोल हैं, क्योंकि लोडिंग के शुरुआती चरणों में सटीकता इतनी महत्वपूर्ण नहीं है, लेकिन कोडिंग की लंबाई पर कोडिंग का सकारात्मक प्रभाव पड़ता है, क्योंकि प्रत्येक चरण अपनी हफ़मैन तालिका का उपयोग करता है।

दोषरहित विधा

दोषरहित संपीड़न। डीसीटी नं। तीन पड़ोसी लोगों में 4 वें बिंदु की भविष्यवाणी का उपयोग किया जाता है। भविष्यवाणी की त्रुटियों को हफमैन द्वारा एन्कोड किया गया है। मेरी राय में, यह कभी-कभी नहीं की तुलना में थोड़ा अधिक उपयोग किया जाता है।

पदानुक्रमित मोड

विभिन्न प्रस्तावों के साथ कई परतें छवि से बनाई गई हैं। पहले मोटे लेयर को हमेशा की तरह एनकोड किया जाता है, और फिर लेयर्स के बीच केवल अंतर (इमेज को रिफाइनमेंट) किया जाता है (Haar wavelet होने का नाटक करता है)। कोडिंग के लिए, DCT या दोषरहित का उपयोग किया जाता है। मेरी राय में, यह कभी नहीं की तुलना में थोड़ा कम प्रयोग किया जाता है।

अंकगणित कोडिंग

हफ़मैन एल्गोरिथ्म पात्रों के वजन के लिए इष्टतम कोड बनाता है, लेकिन यह केवल कोड वाले वर्णों के निश्चित मिलान के लिए सही है। अंकगणित में ऐसी तंग बंधन नहीं है जो आपको कोड का उपयोग करने की अनुमति देता है जैसे कि बिट्स की एक आंशिक संख्या के साथ। यह दावा किया जाता है कि यह हफमैन की तुलना में फ़ाइल का आकार औसतन 10% कम करता है। पेटेंट मुद्दों के कारण सामान्य नहीं, सभी समर्थित नहीं हैं।

मुझे उम्मीद है कि अब आप JPEG एल्गोरिथम को सहज रूप से समझ गए हैं। पढ़ने के लिए धन्यवाद!

युपीडी
वैनविन ने उपयोग किए गए सॉफ़्टवेयर को निर्दिष्ट करने का सुझाव दिया। मुझे यह बताते हुए प्रसन्नता हो रही है कि सभी उपलब्ध हैं और नि: शुल्क हैं:

• पायथन + न्यूम्पी + माटप्लोटिब + पीआईएल (पिलो) । मुख्य उपकरण। के जारी होने पर मिला "मतलाब मुफ्त विकल्प।" मैं इसे सुझाता हूं! Python, .
• JpegSnoop . jpeg-.
• yEd . .
• Inkscape . , . , .
• Daum Equation Editor . , Latex- . Daum Equation — , . , Latex.
• FastStone . , .
• PicPick . SnagIt. , . , , , .