👩🏼‍🚒 👃🏻 〽️ जूलिया सेट का निर्माण 🐯 🕒 🚟

नमस्कार। जुनून उबलता है, वर्ष का अंत, सत्र, समय सीमा, नया साल, साथ ही सेंसरशिप इंटरनेट की सभी परतों में प्रवेश करती है, जो शोक नहीं कर सकती है। हब्र अब केक नहीं है । मैं सिर्फ यह लिखना चाहता था कि मैं इस दृष्टिकोण से सहमत नहीं हूं, लेकिन तब मैं सिर्फ प्रतिबंध लगाऊंगा। इसलिए आपको दिलचस्प सामग्री लिखनी होगी। हालांकि अगर जूलिया सेट के बारे में पोस्ट के परिचय के कारण उन्हें प्रतिबंधित कर दिया गया है, ठीक है, तो केक के अवशेष गिर गए हैं और कोई मौका नहीं है।

तो, पोस्ट के विषय पर वापस जाएं। मैं लंबे समय से जटिल संख्याओं के बारे में थोड़ा और सीखना चाहता हूं, न कि केवल माइनस एक की जड़ मैं है। विशेष रूप से दिलचस्प एक भग्न संरचना के साथ आंकड़े थे, मैं यह समझना चाहता था कि इसका क्या मतलब है और इस तरह के एक दृश्य को कैसे बनाया जाए। शेल्फ पर कहीं टीएफकेपी पर एक किताब थी, साथ ही साथ कर्सर पर जटिल विश्लेषण पर एक कोर्स समाप्त हो गया , और थोड़ा खाली समय दिखाई दिया। चलिए शुरू करते हैं।

फंक्शन पुनरावृत्ति

एक एल्गोरिथ्म लिखने से पहले, आपको कुछ बुनियादी अवधारणाओं को सीखना होगा। हम एक फ़ंक्शन को पुनरावृत्त करने की अवधारणा के साथ शुरू करते हैं। हम f की nth पुनरावृत्ति के लिए निम्नलिखित संकेतन प्रस्तुत करते हैं:

जहां साइन ○ फ़ंक्शन की एक संरचना है

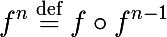पहचान मानचित्रण को शून्य पुनरावृत्ति के रूप में लिया जाता है:

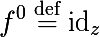
कुछ प्रकार के मैपिंग के निश्चित बिंदुओं पर कई प्रमेय हैं, याद रखें कि कुछ मैपिंग जी का एक निश्चित बिंदु क्या है, यह निम्नलिखित समीकरण का समाधान है:

इसी प्रकार, किसी फ़ंक्शन के पुनरावृत्ति के लिए, एक आकर्षित करने वाला बिंदु पेश किया जाता है - फ़ंक्शन f के डोमेन से ऐसा बिंदु जिसे फ़ंक्शन f के पुनरावृत्तियों का क्रम मैप f के कुछ निश्चित बिंदु में परिवर्तित करता है:

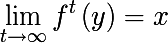
जहां y कुछ बिंदु पर्याप्त रूप से x के करीब है

पिछली स्थिति को पूरा करने वाले सभी y के सेट को फ़ंक्शन f के पुनरावृत्ति के तहत बिंदु x की सीमा सेट कहा जाता है।

एक नियम के रूप में, यह पुनरावृत्तियों द्वारा गठित कार्यों के अनुक्रम का अध्ययन करने के लिए रुचि है (एक समान विचार न्यूटन विधि में देखा जा सकता है, वांछित समाधान निर्मित नक्शे का एक आकर्षक निश्चित बिंदु निकला, और इसलिए इसे पुनरावृत्ति अनुक्रम की सीमा के रूप में पाया जा सकता है।)

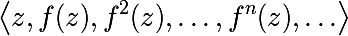
साथ ही कुछ शुरुआती बिंदु पर गणना की गई मूल्यों का एक क्रम

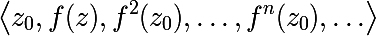
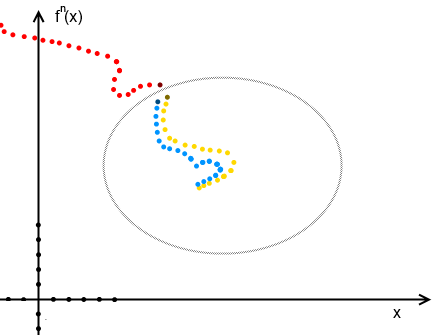
जटिल दुनिया के लिए, फ़ंक्शन च के पुनरावृत्ति के तहत बिंदु y से x के पुनरावृत्त अभिसरण की कल्पना करना थोड़ा समस्याग्रस्त है, सभी एक ही 4d है, लेकिन वास्तविक दुनिया के लिए चित्र केवल 2d (लाल पथ विचलन है, जबकि नीला एक निश्चित बिंदु में परिवर्तित होता है)।

तो, जूलिया सेट को समझने के लिए पहला कंकड़ आवश्यक रखा गया है, चलो अगले पर चलते हैं।

द्विघात जटिल बहुपद

सामान्य तौर पर, जूलिया सेट का निर्माण कार्य के लिए किया जाता है

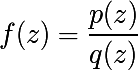
जहाँ p और q जटिल बहुपद हैं

हम समस्या को सरल करेंगे, और हम जूलिया का निर्माण केवल द्विघात बहुपद के लिए करेंगे। सामान्य रूप में द्विघात जटिल बहुपद इस प्रकार है:

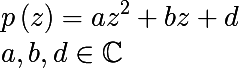
वहाँ एक एकात्मक ( a = 1 ) केन्द्रित ( b = 0 ) एक द्विघात बहुपद का रूप की अवधारणा भी है

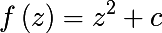
हम निम्नलिखित मानचित्र का परिचय देते हैं और इसका उलटा नक्शा पाते हैं:

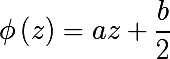
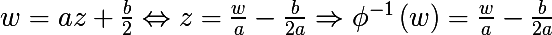
निम्नलिखित अभिव्यक्ति पर विचार करें

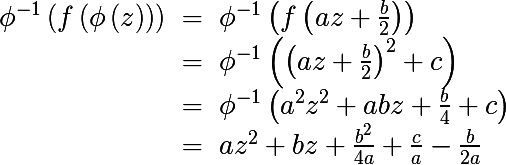
यह देखना आसान है कि अंतिम अभिव्यक्ति सामान्य रूप p (z) में एक द्विघात बहुपद से मिलती जुलती है, आइए c को ऐसे खोजें कि परिणामी अभिव्यक्ति सामान्य रूप के द्विघात बहुपद में कम हो।

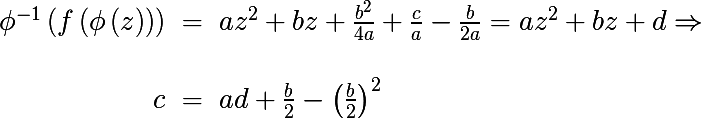
इस प्रकार, हमने दिखाया कि सी के उपर्युक्त प्रतिस्थापन के साथ, सामान्य रूप के एक बहुपद के रूप में लिखा जा सकता है

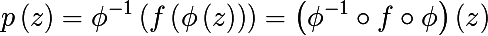
पुनरावृत्तियों की कार्रवाई के तहत एक द्विघात बहुपद का व्यवहार

चलो जूलिया सेट को समझने के लिए आधार के तीसरे कंकड़ पर चलते हैं। जटिल द्विघात बहुपद के दूसरे पुनरावृत्ति पर विचार करें

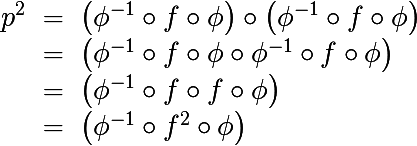
यह दिखाना मुश्किल नहीं है

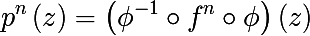
और बस यहां हम तीनों बिंदुओं को जोड़ते हैं, चलो एक निष्कर्ष तैयार करते हैं: पुनरावृत्तियों की कार्रवाई के तहत एक द्विघात बहुपद के व्यवहार की जांच करने के लिए, यह एकात्मक केंद्रित रूप में इसकी जांच करने के लिए पर्याप्त है, और सामान्य रूप में नहीं । और यह वास्तव में अच्छा है, क्योंकि सामान्य शब्दों में हमारे पास तीन गुणांक हैं, और एकात्मक केंद्रित रूप में, केवल एक।

अराजक और सामान्य व्यवहार

जल्द ही जूलिया सेट की परिभाषा देना संभव होगा। हम कड़ाई से गणितीय लोगों के बजाय सहज परिभाषाओं पर विचार करेंगे। लेकिन पहले, स्थिरता की अवधारणा पर विचार करें। एक निश्चित अंतर समीकरण के समाधान को स्थिर कहा जाता है यदि प्रारंभिक के करीब स्थितियों के साथ समाधान का व्यवहार मूल समाधान के व्यवहार से बहुत भिन्न नहीं होता है । यह अनुमान लगाना मुश्किल नहीं है कि वाक्यांश में सभी नमक बहुत अलग नहीं हैं । सामान्य तौर पर, विभिन्न प्रकार की स्थिरता को प्रतिष्ठित किया जाता है, उदाहरण के लिए, ल्यपुनोव स्थिरता जूलिया सेट की परिभाषा में शामिल है (यह स्पष्ट परिभाषा कार्यों के एक कॉम्पैक्ट परिवार पर मोंटेल प्रमेय से अनुसरण करती है), लेकिन हम स्थिरता में मतभेदों के सार में भी नहीं जाएंगे, मुख्य बात यह है कि विचार को समझना है। आइए इसका उदाहरण देने की कोशिश करते हैं। शुरुआत करने के लिए, आइए स्थिरता की सहज धारणा पर एक नज़र डालें, यहाँ बिंदुओं के नीले और पीले प्रक्षेपवक्र एक छोटे से परिवर्तन के साथ लगभग समान व्यवहार करते हैं, जबकि लाल प्रक्षेपवक्र के लिए, एक छोटा परिवर्तन पूरी तरह से अलग दिशा में जाता है।

आइए निम्नलिखित बहुपद f (z) = z ² - 1 + 0.213i पर विचार करें और z ₀ = 0.3 + 0.2i और z ₀ = 0.31 + 0.2i पर 100 पुनरावृत्तियों के लिए एक प्रक्षेपवक्र का निर्माण करें ।

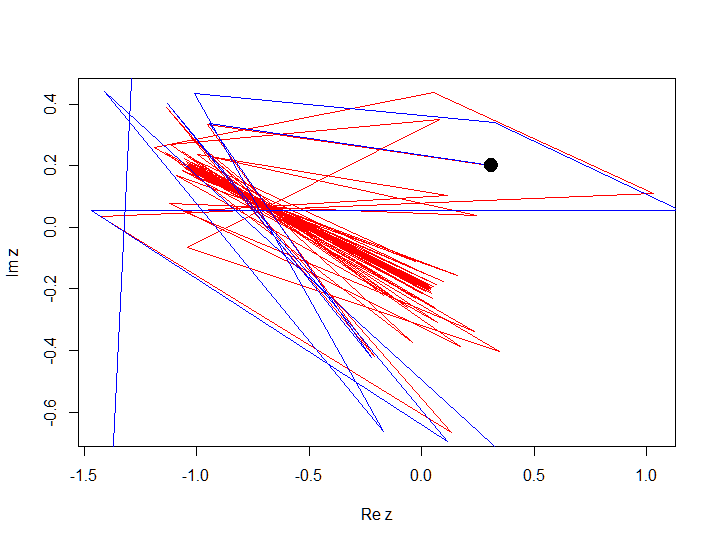
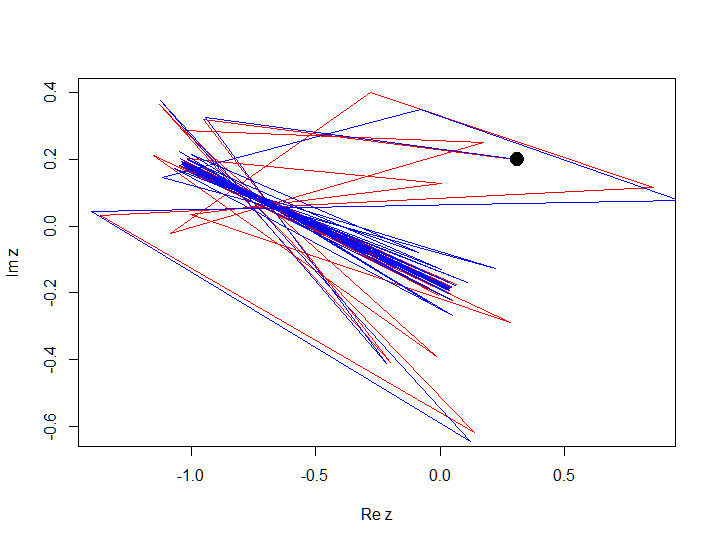
इस उदाहरण में, आप देखते हैं कि प्रारंभिक स्थिति में एक छोटे से परिवर्तन से प्रक्षेपवक्र का विचलन हुआ, हम इस व्यवहार को शुरुआती बिंदु के कुछ पड़ोस में अराजक कहते हैं, अर्थात्। व्यवहार प्रारंभिक स्थितियों में छोटे बदलावों पर अत्यधिक निर्भर है। जबकि व्यवहार जिसमें स्थिरता बनी रहती है, अर्थात्। प्रारंभिक स्थितियों में छोटे परिवर्तन एक पूरे के रूप में व्यवहार को बहुत प्रभावित नहीं करते हैं, हम निम्न उदाहरण में, सामान्य कहेंगे। निम्नलिखित बहुपद f (z) = z ² - 1 + 0.2i पर विचार करें (बस निरंतर ग को बदला), और z ₀ = 0.3 + 0.2i और z ₀ = 0.31 + 0.2i पर 100 पुनरावृत्तियों के लिए प्रक्षेपवक्र का निर्माण करें ।

फतौ, जूलिया और मैंडेलब्रोट के समूह

बहुपद f (z) = z ² + c का एक फ़ाटो सेट प्रत्येक बिंदु के लिए जटिल संख्याओं के सेट का एक उपसमूह है जिसमें पुनरावृत्तियों की कार्रवाई के तहत कार्य का व्यवहार सामान्य है , अर्थात पुनरावृत्तियों द्वारा उत्पन्न बिंदुओं के प्रक्षेपवक्र में बहुत अधिक परिवर्तन नहीं होता है जब प्रारंभिक स्थिति प्रारंभिक बिंदु के कुछ छोटे पड़ोस में बदल जाती है। इसे F (f) द्वारा दर्शाया जाता है।
क्रमशः बहुपद f (z) = z ² + c का जूलिया सेट , जटिल संख्याओं के सेट के ऐसे सबसेट को संदर्भित करता है, जिसके प्रत्येक बिंदु के लिए पुनरावृत्तियों की क्रिया के तहत कार्य का व्यवहार अव्यवस्थित है , अर्थात्। प्रारंभिक बिंदु के कुछ छोटे पड़ोस में प्रारंभिक स्थितियों में छोटे परिवर्तन महत्वपूर्ण रूप से प्रक्षेपवक्र को प्रभावित करते हैं। J (f) द्वारा अस्वीकृत
मैंडेलब्रॉट सेट बहुपद f (z) = z ² + c के मापदंडों का ऐसा समूह है, जिसके लिए जूलिया सेट जुड़ा हुआ है ।

आकर्षक ताल

इसलिए हमने जूलिया सेट का अर्थ सीखा, हम इस तरह के सेट के निर्माण के लिए एल्गोरिथ्म पर आगे बढ़ सकते हैं। लेकिन इसके लिए, आपको पहले कुछ अन्य परिभाषाएँ प्रस्तुत करनी होंगी।

एक आकर्षित करने वाला एक गतिशील प्रणाली के राज्यों का एक सेट है, जिस दिशा में समय के साथ प्रणाली विकसित होती है। हमारे मामले में, हम एक नियोजक को निश्चित बिंदुओं के सबसेट के रूप में समझ सकते हैं, जो किसी फ़ंक्शन के पुनरावृत्तियों के अनुक्रमों को प्रारंभिक स्थितियों की परवाह किए बिना परिवर्तित करते हैं।
फ़ंक्शन f के बिंदु z का एक आकर्षित करने वाला पूल, z के पड़ोस ( A (z) द्वारा निरूपित ) से अंकों का एक सबसेट है, जैसे कि इनमें से किसी एक बिंदु पर शुरू किया गया कोई भी प्रक्षेप z में परिवर्तित होता है
अनन्तता के प्रति आकर्षण पूल A (attract) से हमारा तात्पर्य उन बिंदुओं z के समुच्चय से है जिसके लिए प्रक्षेपवक्र अनंत तक जाते हैं, अर्थात। दूसरे शब्दों में, वे किसी निश्चित बिंदु पर नहीं मिलते हैं, और न ही वे दो या दो से अधिक आवधिक बिंदुओं के बीच दोलन करते हैं (एक निश्चित बिंदु एक आवधिक बिंदु है जो एक के बराबर अवधि है)।

कुछ बहुपद f (z) = z ² + c के लिए हमारे तर्क के संदर्भ में A ( for ) पर विचार करें

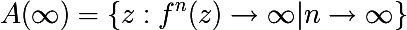
यह पता चला है कि निम्नलिखित प्रमेय मौजूद है। सेट ए ( set ) (उपरोक्त संदर्भ में) खुला , जुड़ा हुआ है, और अनबाउंड है । यह पूरी तरह से फतौ सेट में निहित है। जूलिया सेट सीमा ए ( which ) के साथ मेल खाता है, जो सभी जटिल संख्याओं का एक बंद और घिरा हुआ सबसेट है।

जूलिया सेट का निर्माण

मैं आपको याद दिलाता हूं कि हम द्विघात गतिशीलता के जूलिया सेट के निर्माण के लिए एक एल्गोरिथ्म लिखेंगे, और किसी भी फ़ंक्शन को नहीं। इसलिए हमने सीखा कि जूलिया सेट सीमा ए ( which ) के साथ मेल खाता है, जो सभी जटिल संख्याओं का एक बंद और बाउंडेड सबसेट है, अर्थात। जूलिया सेट भी बंद और बाउंडेड है। हमें निरूपित करते हैं, जो फ़ंक्शन संख्या के पुनरावृत्तियों द्वारा उत्पन्न जटिल संख्याओं के सबसेट के रूप में निम्नानुसार है और बद्ध रहता है। हम ऐसे सेट को एक भरा हुआ जूलिया सेट कहते हैं :

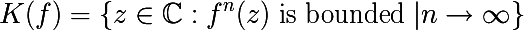
और अंतिम प्रमेय जिसकी हमें आवश्यकता है वह इस प्रकार है:

आज्ञा देना कुछ द्विघात बहुपद के रूप में f (z) = z ² + c
लक्षित
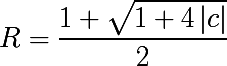
फिर कुछ बिंदु के लिए 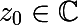और n> 0 निम्नलिखित स्थिति संतुष्ट है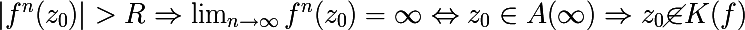
यानी यदि nth पुनरावृत्ति का मापांक R से अधिक है, तो फ़ंक्शन f का विचलन f diverge होता है, यह बिंदु z _{0 के} बराबर होता है, जो कि अनन्तता के लिए आकर्षित करने वाले पूल में प्रवेश करता है, जिसका अर्थ है कि z ₀ भरा हुआ जूलिया सेट का बिंदु नहीं है।

एल्गोरिथ्म के अलावा, कोई भी इस प्रमेय से यह निष्कर्ष निकाल सकता है कि पूरा जूलिया सेट मूल पर केंद्रित त्रिज्या आर की एक गेंद के अंदर है।

पुनश्च: यहाँ के बारे में प्रेमियों के डिजाइन और सुनहरे वर्गों, मनीषियों और मनोगत, ध्यान देंगे कि f (z) = z ² + 1 के लिए , दहलीज R स्वर्ण खंड o_0 के बराबर है

एल्गोरिथ्म

बहुपद f (z) = z ² + c निर्दिष्ट करने के लिए c चुनें
हम किसी दिए गए बहुपद f (z) = z ² + c के लिए R की गणना करते हैं
हम अधिकतम पुनरावृत्ति को इंगित करने के लिए अधिकतम पैरामीटर का चयन करते हैं, जाहिर है कि यह अधिक है, बेहतर सटीकता, एल्गोरिथ्म में धीमी गति।
हम रंगों की एक सरणी उत्पन्न करते हैं, कुल अधिकतम टुकड़े, उज्ज्वल से कम उज्ज्वल तक कहते हैं, हम रंग के साथ निरूपित करेंगे, फिर जूलिया सेट से कितनी दूर है
प्रत्येक बिंदु के लिए, हम गणना करते हैं कि क्या यह भरे हुए जूलिया सेट का हिस्सा है या नहीं, साथ ही पुनरावृत्ति संख्या जिस पर सीमा पार हो गई थी
अगर | z | > आर तो पहले रंग का उपयोग करें, फिर उस रोशनी का उपयोग करें जिस पर तिरछा संख्या पार हो गई थी

जूलिया सेट जनरेशन प्रोसीजर

/// <summary> /// Generate bmp with Julia set /// </summary> /// <param name="c">parameter of square dynamics</param> /// <param name="w">width of bmp</param> /// <param name="h">height of bmp</param> /// <param name="maxIter">max iterations of function</param> /// <param name="xMin">window in complex plane</param> /// <param name="yMin">window in complex plane</param> /// <param name="xMax">window in complex plane</param> /// <param name="yMax">window in complex plane</param> /// <returns></returns> static XBitmap PlotJuliaSet(ComplexNumber c, int w, int h, int maxIter, double xMin = Double.NaN, double yMin = Double.NaN, double xMax = Double.NaN, double yMax = Double.NaN) { double r = CalculateR(c); if (Double.IsNaN(xMin) || Double.IsNaN(xMax) || Double.IsNaN(yMin) || Double.IsNaN(yMax)) { xMin = -r; yMin = -r; xMax = r; yMax = r; } Logger.Instance.Log("R = " + r); double xStep = Math.Abs(xMax - xMin) / w; double yStep = Math.Abs(yMax - yMin) / h; XBitmap bmp = new XBitmap(w, h); IDictionary<int, IDictionary<int, int>> xyIdx = new Dictionary<int, IDictionary<int, int>>(); int maxIdx = 0; for (int i = 0; i < w; i++) { xyIdx.Add(i, new Dictionary<int, int>()); for (int j = 0; j < h; j++) { double x = xMin + i * xStep; double y = yMin + j * yStep; ComplexNumber z = new ComplexNumber(x, y); IList<ComplexNumber> zIter = SqPolyIteration(z, c, maxIter, r); int idx = zIter.Count - 1; if (maxIdx < idx) { maxIdx = idx; } xyIdx[i].Add(j, idx); } } for (int i = 0; i < w; i++) { for (int j = 0; j < h; j++) { int idx = xyIdx[i][j]; double x = xMin + i * xStep; double y = yMin + j * yStep; ComplexNumber z = new ComplexNumber(x, y); bmp.SetPixel(w - i - 1, j, ComplexHeatMap(idx, 0, maxIdx, z, r)); } } return bmp; } private static IList<ComplexNumber> SqPolyIteration(ComplexNumber z0, ComplexNumber c, int n, double r = 0) { IList<ComplexNumber> res = new List<ComplexNumber>(); res.Add(z0); for (int i = 0; i < n; i++) { if (r > 0) { if (res.Last().Mod > r) { break; } } res.Add(res.Last() * res.Last() + c); } return res; } private static double CalculateR(ComplexNumber c) { return (1 + Math.Sqrt(1 + 4*c.Mod))/2; } public static Color ComplexHeatMap(decimal value, decimal min, decimal max, ComplexNumber z, double r) { decimal val = (value - min) / (max - min); return Color.FromArgb( 255, Convert.ToByte(255 * val), Convert.ToByte(255 * (1 - val)), Convert.ToByte(255 * (z.Mod / r > 1 ? 1 : z.Mod / r)) ); }

परिणाम

इस सुविधा का उपयोग करके बनाई गई 5k चित्रों में से कुछ 5k हैं

अब आइए बहुपद f (z) = z ² - 0.74543 + 0.11301i के लिए जूलिया सेट के बारे में सोचते हैं, पूरा सेट त्रिज्या 1.50197192317588 की एक गेंद में समाहित है ।

इस तस्वीर में ऐसा लग रहा है कि सटीकता की सीमा पूरी हो गई है, और सभी लाल तत्व जूलिया सेट के हैं। लेकिन यह वहाँ नहीं था, हम अधिकतम पैरामीटर बढ़ाते हैं, और हमें एक और अधिक सटीक अनुमान मिलता है। सामान्य तौर पर, आप अनिश्चित काल तक जारी रख सकते हैं। कोई मजाक नहीं -)

जूलिया सेट का निर्माण

फंक्शन पुनरावृत्ति

द्विघात जटिल बहुपद

पुनरावृत्तियों की कार्रवाई के तहत एक द्विघात बहुपद का व्यवहार

अराजक और सामान्य व्यवहार

फतौ, जूलिया और मैंडेलब्रोट के समूह

आकर्षक ताल

जूलिया सेट का निर्माण

एल्गोरिथ्म

परिणाम

More articles: