यह आलेख बताएगा कि कैसे वुल्फ्राम मैथमेटिका पर्यावरण को अंतर समीकरणों की जटिल प्रणालियों को हल करने के लिए लागू किया जाए, समाधान परिणामों की चित्रमय व्याख्या, शारीरिक समस्याओं के लिए प्रक्रियात्मक प्रोग्रामिंग तत्वों को लागू करना, कठोर शरीर गति के उदाहरण का उपयोग करना। लेख का सार यह दिखाना है कि कैसे, कंप्यूटर बीजगणित उपकरणों का उपयोग करके, 19 वीं शताब्दी के भौतिकविदों के दिमाग को उत्तेजित करने वाले जटिल भौतिक प्रणालियों का विश्लेषण करना आसान और सरल है।
गोलाकार गति के बारे में थोड़ा
गोलाकार गति - एक
टीटी की गति एक निश्चित बिंदु है। इस आंदोलन के साथ
टीटी के प्रत्येक बिंदु संलग्नक के बिंदु पर केंद्र के साथ गोले की सतह के साथ चलते हैं। इस मामले में, एक घूर्णी गति की बात करता है, जो कि फिक्सिंग बिंदु से गुजरने वाले रोटेशन के तात्कालिक अक्षों के चारों ओर प्राथमिक घुमाव की एक श्रृंखला से बना है। रोटेशन की तात्कालिक धुरी लगातार अपनी स्थिति बदलती है, दोनों को संदर्भ फ्रेम के संबंध में जिसमें आंदोलन माना जाता है, और शरीर में ही, इस प्रकार दो विहित सतहों का निर्माण होता है, जिसे क्रमशः फिक्स्ड और मूवेबल एक्सोइड्स कहा जाता है।
एक निश्चित-बिंदु
सीटी में स्वतंत्रता की 3 डिग्री होती है, और किसी दिए गए संदर्भ फ्रेम के संबंध में इसकी स्थिति तीन मापदंडों, या एर्गन बस्तियों द्वारा निर्धारित की जाती है। ये कोण सिस्टम के तीन मोड़ को परिभाषित करते हैं, जो सिस्टम की किसी भी स्थिति को वर्तमान में लाने की अनुमति देते हैं।
यदि हम इसी कोणों
θ, φ , और
les के द्वारा Z, X ', Z' के क्रम में कुल्हाड़ियों Z और X के चारों ओर
SC के प्राथमिक घुमाव को लेते हैं, तो यह परिवर्तन Euler कोणों के संदर्भ में रोटेशन मैट्रिक्स की अभिव्यक्ति की ओर जाता है। ऐसे मैट्रिक्स का उपयोग करके,
टीटी अंतरिक्ष में घूमता है।
उपयोग किए गए कोणों के निम्नलिखित भौतिक अर्थ हैं:
- कोण angle - पूर्वगामी कोण
- कोण angle - पोषण का कोण
- कोण angle - उचित रोटेशन के कोण
टीटी का गोलाकार गति, जिसे पहले लियोनार्ड यूलर (जर्मन: लियोनहार्ड यूलर) द्वारा वर्णित किया गया था, केवल तीन मामलों में एक समाधान है:
- यूलर का मामला - एक टीटी के द्रव्यमान का केंद्र, एक निश्चित बिंदु पर है। बाहरी ताकतों का क्षण शून्य है।
- लैग्रेंज केस - टीटी गतिशील रूप से सममित है
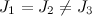। सीटी के द्रव्यमान का केंद्र समरूपता की धुरी पर है। - कोवालेवस्काया का मामला - शरीर गतिशील रूप से सममित है, जड़ता के क्षण संबंध से संबंधित हैं
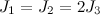। टीटी के द्रव्यमान का केंद्र भूमध्यरेखीय तल में है।
अगला, हम लैग्रेग मामले में एक भारी सममित शीर्ष के आंदोलन के बारे में बात करेंगे।
लैग्रेंज के मामले में गति के समीकरण
आइए हम गुरुत्वाकर्षण के क्षेत्र में एक भारी सममित शीर्ष की एक रेखाचित्र बनाते हैं। शीर्ष की भूमिका शंकु को सौंपी गई है।
हम गतिज गति के समीकरण से गति के समीकरण प्राप्त करते हैं, जो पहले इसे सामान्य रूप में एक चल
SC में लिखा था।
अब हम अपने द्वारा बनाई गई ड्राइंग और नीचे लिखे प्रमेय का उपयोग करेंगे: थकाऊ सूत्रों को छोड़ते हुए, सममित शीर्ष की जड़ता के क्षणों को ध्यान में रखते हुए और समान प्रस्तुत करते हुए, हम गुरुत्वाकर्षण के क्षेत्र में
टीटी की गति के समीकरणों की प्रणाली प्राप्त करते हैं।
इस प्रणाली को सख्ती से विश्लेषणात्मक रूप से हल नहीं किया गया है, और समाधान केवल क्वाड्र्रेज़ में प्रस्तुत किया गया है। हम इस प्रणाली को संख्यात्मक रूप से हल करेंगे और परिणामों का विश्लेषण करेंगे।
वोल्फ्राम मैथेमेटिका प्रणाली में लैगरेंज मामले की मॉडलिंग
शुरू करने के लिए, हमें अपने
रिमोट कंट्रोल सिस्टम के लिए प्रारंभिक शर्तें निर्धारित करने की आवश्यकता है:
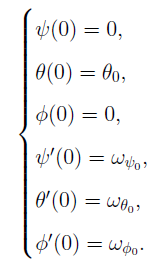
इसके अलावा, एक कंप्यूटर बीजगणित प्रणाली की क्षमताओं का उपयोग करते हुए, हम शीर्ष के मापदंडों को निर्धारित करते हैं, आदिम आकर्षित करते हैं, और
नियंत्रण प्रणाली को संख्यात्मक रूप से हल करते हैं।
फिर हमें रोटेशन मैट्रिक्स मिलता है, जिसके बारे में हमने पहले बात की थी, बिल्ट-इन लैंग्वेज टूल्स का उपयोग करते हुए, वहाँ संख्यात्मक समाधान का विकल्प दिया और इस "केक" के लिए ज्यामितीय परिवर्तन ऑपरेटर को लागू किया:
यह मूल रूप से एक दो लाइनों में समाधान की जटिलता है। यह केवल ग्राफिक क्षेत्र को निर्धारित करने, गति के प्रक्षेपवक्र का निर्माण करने और एक एनीमेशन बनाने के लिए बना हुआ है, लेकिन यह पहले से ही है, जैसा कि वे एक शौकिया से कहते हैं (आप परिवर्तन मैट्रीक के संख्यात्मक व्युत्पत्ति के लिए खुद को सीमित कर सकते हैं)। कोड के बाकी:
वुल्फ्राम मैथमेटिका प्रणाली में परिणामों का निष्कर्ष और विश्लेषण
गति, एनीमेशन समय और शीर्ष की पारदर्शिता की प्रारंभिक स्थितियों के गतिशील मापदंडों के साथ कार्यक्रम के परिणामों का उत्पादन एक खिड़की के रूप में किया जाता है।
आइए गुरुत्वाकर्षण के क्षेत्र में
नियमित (जबरन) पूर्व स्थिति के मामले में शीर्ष के व्यवहार का विश्लेषण करें:
गतिज गति प्रमेय के अनुसार (हमने इसके बारे में ऊपर बात की), समय की हर छोटी अवधि के लिए
, कोणीय गति वेक्टर को गुरुत्वाकर्षण की कार्रवाई के तहत एक वृद्धि प्राप्त होती है।
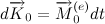
साथ निर्देशित किया
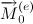
, यानी। शीर्ष की धुरी के लंबवत समतल में स्थित है। यह निम्नानुसार है कि कोणीय गति के वेक्टर और इसके साथ शीर्ष की धुरी समान रूप से (पूर्व में) घूमती है और फुलक्रैम से गुजरने वाली एक ऊर्ध्वाधर रेखा के चारों ओर। ऊर्ध्वाधर शीर्षों पर शीर्ष झुकता है, अर्थात। अपने स्वयं के अक्ष के चारों ओर घूमने के अलावा, यह एक ऊर्ध्वाधर अक्ष के आसपास भी घूमता है। तेजी से उचित रोटेशन के साथ, यह पूर्वताप (ऊर्ध्वाधर अक्ष के चारों ओर घूमना) इतनी धीमी गति से होता है कि अच्छी सटीकता के साथ आप कोणीय गति के घटक की उपेक्षा कर सकते हैं जो ऊर्ध्वाधर के चारों ओर पूर्वसूचना के कारण होता है। शीर्ष अक्ष के इस व्यवहार को नियमित रूप से पूर्वता कहा जाता है। यह एक जबरन छूट है, क्योंकि यह गुरुत्वाकर्षण के क्षण के प्रभाव में होता है। शीर्ष के सभी बिंदु अपनी धुरी पर समान रूप से गोलाकार रास्तों के साथ चलते हैं, जिनमें से केंद्र शीर्ष के फुलक्रम से गुजरते हुए लंबवत होते हैं। दृष्टांत शीर्ष की नियमित पूर्वधारणा को दर्शाता है।
यह घटना केवल कड़ाई से परिभाषित प्रारंभिक शर्तों के तहत होती है।
अब हम इस सवाल का अध्ययन करने के लिए आगे बढ़ सकते हैं कि एक कताई शीर्ष कैसे प्रारंभिक परिस्थितियों में गुरुत्वाकर्षण की कार्रवाई के तहत व्यवहार करेगा जो एक नियमित रूप से रियायत की तत्काल घटना प्रदान नहीं करता है। सामान्य मामले में, शीर्ष की गति को मजबूर नियमित रूप से रियायत और पोषण का एक सुपरपोजिशन होना चाहिए, जैसा कि आंकड़े में दिखाया गया है।
पहले क्षण में, जैसे ही हम गुरुत्वाकर्षण के प्रभाव के तहत शीर्ष की धुरी को छोड़ते हैं, यह वास्तव में नीचे गिरना शुरू हो जाता है, जो हमारे सहज विचारों के अनुरूप है। लेकिन जैसे-जैसे धुरी गति पकड़ती है, इसके ऊपरी सिरे का प्रक्षेप ऊर्ध्वाधर से अधिक से अधिक विचलन करता है। जल्द ही, धुरी की गति क्षैतिज हो जाती है, जैसा कि एक नियमित पूर्वसर्ग के साथ होता है, लेकिन इस गति की गति एक नियमित रूप से छूट के लिए आवश्यक से अधिक है। अक्ष के अंत का प्रक्षेपवक्र ऊपर की ओर विचलन करने लगता है। अपनी मूल ऊँचाई तक बढ़ने के बाद, अक्ष "जमा देता है" - इसकी गति लुप्त हो जाती है। फिर सब कुछ पहले दोहराता है। लेकिन अब हम समझते हैं कि किस तरह का व्यवहार होता है, जब अक्ष का अंत एक चक्रवाती प्रक्षेपवक्र के साथ चलता है, तो इसे दो आंदोलनों के अतिरिक्त द्वारा समझाया गया है - कोणीय गति वेक्टर के चारों ओर शीर्ष का पोषण एक साथ ऊर्ध्वाधर के चारों ओर इस वेक्टर की जबरन प्रबलता के साथ।
जब पोषण छोटे होते हैं, तो जबरन प्रीसेशन को छद्म-नियमित कहा जाता है, आकृति में हम इस घटना का निरीक्षण कर सकते हैं। तेजी से घूमने वाले जाइरोस्कोप (यानी, बहुत तेजी से घूमने वाले गायरोस्कोप) तकनीक में इस्तेमाल किए जाने के लिए, छद्म-नियमित पूर्वधारणा व्यावहारिक रूप से नियमित से अलग नहीं होती है। ऐसे मामलों में, पोषण खुद को बमुश्किल ध्यान देने योग्य छोटे और अक्सर गाइरोस्कोप की धुरी के कंपकंपी के रूप में प्रकट होता है। इसके अलावा, घर्षण बलों की कार्रवाई के तहत छोटे पैमाने पर पोषण जल्दी से क्षय हो जाता है, और छद्म-नियमित पूर्वधारणा नियमित हो जाती है।
निष्कर्ष
इस प्रकार, वुल्फराम मैथमेटिका के रूप में इस तरह के एक शक्तिशाली उपकरण का उपयोग करना, हम प्रोग्रामिंग के बारे में बहुत प्रयास और ज्ञान के बिना कर सकते हैं, और सबसे महत्वपूर्ण बात यह है कि क्लासिक पाठ्यपुस्तकों का सुझाव है, दिलचस्प और रहस्यमय प्रक्रियाओं और घटनाओं का निरीक्षण करें। मुख्य बात यह है कि हम स्वतंत्र रूप से सिस्टम के किसी भी पैरामीटर को मोड़ सकते हैं और घुमा सकते हैं, जो समझने के लिए बहुत महत्वपूर्ण है। यह प्रोजेक्ट मेरा टर्म पेपर था, मैं इस पर कुछ महीनों तक बैठा रहा, लेकिन मैं परिणाम से खुश था। एक लंबे समय के लिए मैंने अपने शीर्ष की गति के एनीमेशन को घुमा दिया और विभिन्न गति प्रक्षेपवक्रों को देखने वाले मापदंडों के साथ खेला, जो लाग्रेंज या कोवालेवस्काया के पास नहीं था।
साहित्य
- Wittenburg, जे। ठोस के गतिशीलता / जे। Wittenburg.- मास्को: MIR, 1980.-294 पी .:
- घूर्णी गति।
- यूलर कोण।
- जाइरोस्कोप की जबरन पूर्वता।
युपीडी। श्रमिकों के अनुरोध पर ड्रॉपबॉक्स पर परियोजना अपलोड की गई
वोल्फ्राम मैथमेटिका 9.0 द्वारा उपयोग किया जाता है
- सीडीएफ परियोजना।
- नायब परियोजना।