हम गणना करते हैं कि पायथन में बिग बैंग किस वर्ष से है

क्रिसमस से आने वाले वर्ष 2014 के संबंध में, सवाल उठ सकता है: "यह वास्तव में धर्म के बिना कौन सा वर्ष है?"

हम उस क्षण से गिनती करेंगे जब ब्रह्मांड शुरू होता है, यानी बिग बैंग। कोड की न्यूनतम संख्या के फार्मूले और लाइनों के लिए परिणाम प्राप्त करने के लिए मैं कई आरक्षणों को छोड़ दूंगा (हाँ, हम पायथन में कार्यक्रम करेंगे!)। एक बोनस के रूप में, हम यह भी अनुमान लगाएंगे कि ब्रह्मांड में कितनी गहरी ऊर्जा है।


हबल स्पेस टेलीस्कोप के साथ देखा गया सुपरनोवा 1994D। फोटो: पीट चालिस - हार्वर्ड स्मिथसोनियन सेंटर ऑफ एस्ट्रोफिजिक्स

जानना चाहते हैं? तो फिर चलिए!

संक्षेप में मुद्दे के भौतिक पक्ष के बारे में

क्या आपने हबल के बारे में सुना है? उनके नाम पर एक दूरबीन भी है। इसलिए उन्होंने इस तथ्य की खोज की कि यूनिवर्स आकार में विस्तार कर रहा है, या यूँ कहें कि आस-पास की आकाशगंगाएँ बिखर रही हैं, और वे हमसे जितना दूर हैं, उतनी ही तेज़ी से वे दूर चले जाते हैं। ब्रह्मांड कैसे बढ़ सकता है? सादृश्य सरल हो सकता है। एक गुब्बारे पर एक चींटी के रूप में खुद को कल्पना करो। यह आपको प्रतीत होगा कि दुनिया धीरे-धीरे विस्तार कर रही है, और गेंद पर अन्य चींटियां दूर और आगे निकल रही हैं, हालांकि आपके शरीर के लिए कुछ भी नहीं होता है।

हबल से लौटना। उन्होंने इस तथ्य को कैसे स्थापित किया? दो बिंदु हैं:

• सबसे पहले, आपको आकाशगंगा की गति को मापने की आवश्यकता है। यहां हमें डॉपलर प्रभाव की आवश्यकता है। हम सभी इस समय ट्रेन के सीटी बजाने के साथ क्लासिक प्रयोग के बारे में जानते हैं जब यह प्लेटफॉर्म के साथ स्वीप करता है। जब कोई वस्तु हमसे दूर जाती है, तो उसके द्वारा उत्सर्जित तरंगदैर्ध्य लंबी हो जाती है। इस सुधार से आप गति पा सकते हैं। खगोल विज्ञान में, इस वृद्धि को रेडशिफ्ट कहा जाता है और इसे अक्षर z द्वारा निरूपित किया जाता है। कुछ ज्ञात वर्णक्रमीय रेखा का निरीक्षण करें और इसके विस्थापन का पता लगाकर गति की गणना करें।
• दूसरी बात, आकाशगंगा की दूरी। सिर्फ इसलिए कि उनसे दूरी नहीं नापी जा सकती। यहां हमें पहले से ही एक अतिरिक्त ऑब्जेक्ट की आवश्यकता है - Ia सुपरनोवा टाइप करें। ये तारों के ऐसे विस्फोट होते हैं, जिनमें समान मात्रा में ऊर्जा निकलती है। हम जो चमक देखते हैं, उससे हम विस्फोट की दूरी की गणना स्वयं और उस आकाशगंगा में कर सकते हैं जिसमें यह विस्फोट हुआ था। ऊपर चित्रित एक आकाशगंगा और एक सुपरनोवा विस्फोट है। चमक के मामले में, यह पूरी गैलेक्सी को पीछे छोड़ देता है, जिसमें लगभग एक सौ बिलियन सितारे हैं।

और ब्रह्माण्ड की आयु कहाँ है?

यह मापने से कि ब्रह्मांड कितनी तेजी से बढ़ रहा है, हम यह पता लगा सकते हैं कि यह एक बिंदु कब था। इस क्षण को सब कुछ की शुरुआत कहा जा सकता है और अनुमान लगा सकते हैं कि यह कितने साल पहले था।

सिस्टम तैयार करें

हमें पायथन की आवश्यकता होगी (संस्करण महत्वपूर्ण नहीं है, मैं 2.7 का उपयोग करूंगा। 3. * के साथ अंतर न्यूनतम हैं)
sudo apt-get install python
गणना के लिए, हम Numpy और Scipy का उपयोग करेंगे:
pip install numpy
pip install scipy
और माटप्लोटलिब चार्ट के लिए:
pip install matplotlib

बिना जड़ के सज्जनों के लिए, मैं ऐसी सभा को सलाह देता हूं: store.continuum.io/cshop/anaconda
विंडोज उपयोगकर्ताओं के लिए: code.google.com/p/pythonxy

हम मानते हैं कि सिस्टम तैयार किया गया था। जो कुछ भी आगे बढ़ता है वह अंतःक्रियात्मक रूप से (सीधे पायथन कंसोल में), या iPython में लॉन्च किया जा सकता है। जो आपको पसंद हो

डेटा डाउनलोड करें

आधुनिक खगोल भौतिकी की सुंदरता अवलोकन डेटा का पूर्ण खुलापन है। हम Ia सुपरनोवा प्रकार की इस सूची का उपयोग करेंगे, जिसके बारे में मैंने ऊपर लिखा है: supernova.lbl.gov/Union
हमें इस फ़ाइल की आवश्यकता है: supernova.lbl.gov/Union/figures/SCPUnion2.1_mu_vs_z.txt

कोड लिखना शुरू करें

बाद में आवश्यक पुस्तकालयों को कनेक्ट करें।

 import numpy as np import matplotlib.pyplot as plt 

फ़ाइल से डेटा लोड करें और तीन सहायक सरणियाँ बनाएँ:

 #  5  ,        . #  0 ,    ,       data=np.loadtxt('SCPUnion2.1_mu_vs_z.txt',skiprows=5,converters={0: lambda s: 0}) #         z = data[:,1] #    distance modulus        DM = data[:,2] DM_err=data[:,3] 

दूरी मापांक क्या है और इससे किसी वस्तु की दूरी कैसे प्राप्त होती है, यह पूरी तरह से बेलारूसी विकिपीडिया पर लिखा गया है।

हम इस मात्रा को परिवर्तित करते हैं, जिसका अस्तित्व केवल पर्यवेक्षकों की सुविधा के कारण होता है, भौतिक रूप से। ऑब्जेक्ट की दूरी DL सरणी के लिए लिखी गई है:

 #    def DM2DL(DM): return 10**(DM/5-1)/1e4 #     DL=DM2DL(DM) 

दूरी मापांक की गणना करते समय, कैटलॉग लेखकों ने सुझाव दिया कि सुपरनोवा की चमक -19.3 है, जिसे विवरण में वर्णित किया गया है। उन्होंने हमारे लिए यह काम किया।

अब चर z में हमारे पास रेडशिफ्ट्स हैं और डीएल में मेगापार्सेक में दूरी (1 पारसेक = 3e16 मीटर = 3.3 प्रकाश वर्ष) है। आप एक चित्र बना सकते हैं और देख सकते हैं कि क्या हुआ:

 plt.plot(DL,z,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$z$',size=18) 

अब रेडशिफ्ट, z को गति में परिवर्तित करते हैं। सबसे पहले, हमें गति को रेडशिफ्ट में बदलने के लिए एक फ़ंक्शन की आवश्यकता होती है, अर्थात, उलटा कार्य:

 #        #   c=29979245800 # cm/s #       def v2z(v): return sqrt((1.0+v/c)/(1.0-v/c))-1.0 

सूत्र यहाँ से लिया गया है: en.wikipedia.org/wiki/Redshift#Redshift_formulae

विपरीत दिशा में रूपांतरण के लिए, हम z_list और v_list के बीच पत्राचार की पूर्व गणना करेंगे, जिसके बाद हम एक फ़ंक्शन लिखेंगे जो अंकों के बीच में अंतर करता है:

 v_list=linspace(0,c,100) z_list=v2z(v_list) # plt.plot(z_list,v_list) def z2v(z): return np.interp(z,z_list,v_list)/1e5 v=z2v(z) # km/s 

आइए, हम से इसकी दूरी के आधार पर वस्तु की गति देखें:

 plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18) 

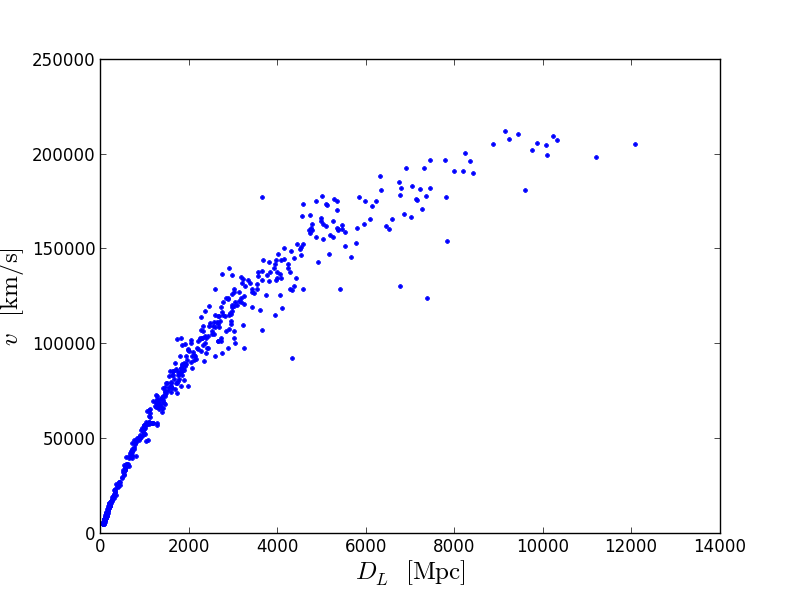
यह तस्वीर स्पष्ट रूप से दिखाती है कि वस्तु जितनी दूर है, उतनी ही तेजी से वह हमसे दूर जाती है। आइए रेखा को लाभ पहुंचाने की कोशिश करते हैं। बिंदु 0 पर रेखा (व्युत्पन्न) की ढलान को हबल स्थिरांक, H कहा जाता है, और किमी / सेकंड में मापा जाता है। आप ढलान द्वारा इस ढलान को पा सकते हैं, लेकिन हम सरल तरीके से जाएंगे। बस ढलान उठाओ:

 plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18) temp=np.array([0.0,20.0]) plt.plot(temp,50.0*temp,'r') plt.plot(temp,70.0*temp,'g') plt.plot(temp,100.0*temp,'m') plt.legend(('data','H=50','H=70','H=100')) 

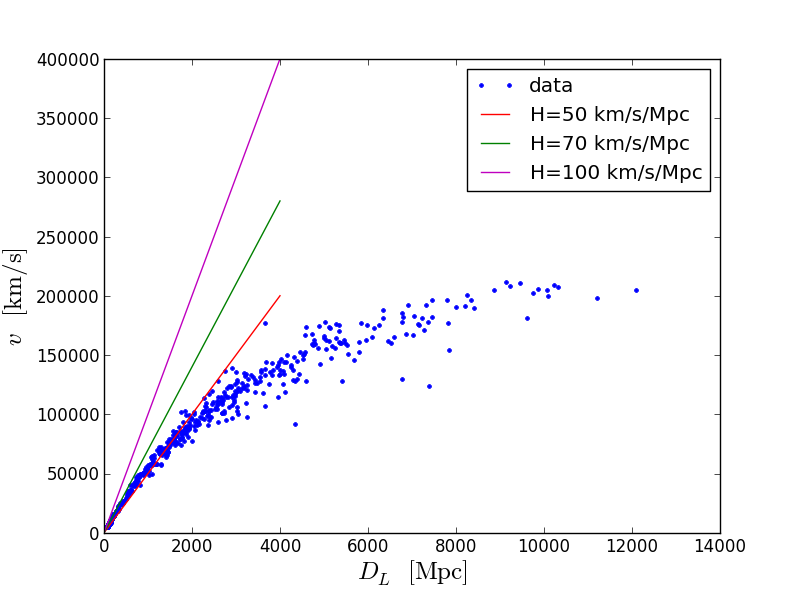
और एक बड़ा संस्करण:


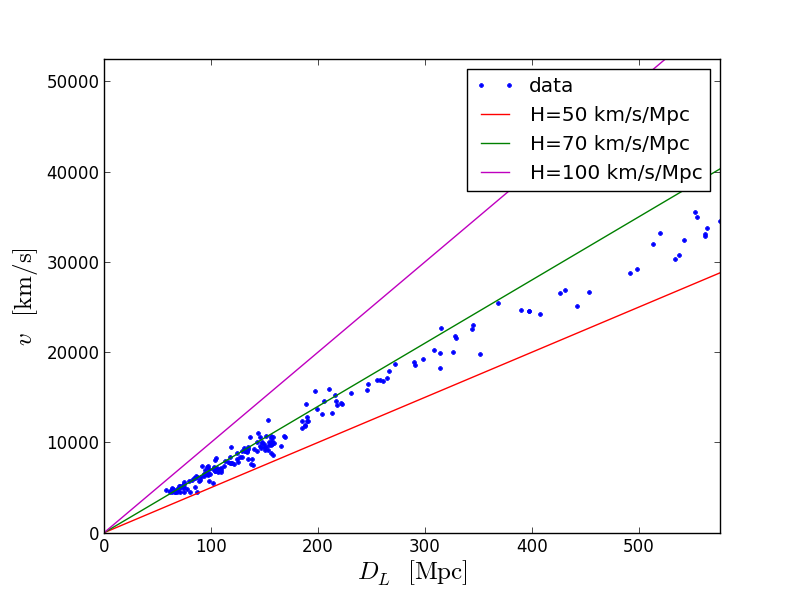
सबसे सटीक अनुमान: एच = 70 किमी / एसपीएस। अर्थात्, हमसे दूर 1 Mpc पर स्थित कोई वस्तु 70 किमी / सेकंड की गति से घूम रही है। दूसरे शब्दों में, वह और मैं इतने साल पहले एक ही बिंदु पर थे (यह मानते हुए कि फैलाव की गति स्थिर थी):

(1 एमपीसी) / (70 किमी / सेकंड) = 1 / एच = 14,000,000,000 साल पहले

( Google माप की विभिन्न इकाइयों को परिवर्तित करने का अच्छा काम करता है।)

कुल मिलाकर, कोड की कुछ पंक्तियों के बाद, हमने पाया कि ब्रह्मांड की आयु लगभग 14 बिलियन वर्ष है। सबसे पहले, यह एक बहुत ही मोटा आकलन है। दूसरे, हमने माप त्रुटि का मूल्यांकन नहीं किया, जिसे किसी भी प्रयोग के साथ किया जाना चाहिए। हमने यह भी नहीं कहा कि हम सुपरनोवा विस्फोटों की चमक कैसे जानते हैं, और हम उन्हें क्यों मानते हैं। ये अलग से दिलचस्प विषय भी हैं। फिर भी, इस तरह का मोटा मूल्यांकन एक अच्छा परिणाम देता है! सभी ज्ञात अवलोकनों के साथ एक अधिक सटीक विश्लेषण 13.813 billion 0.058 बिलियन वर्ष का परिणाम देता है।

उस समय हबल ने केवल इस तरह के आरेख की शुरुआत की थी (उनके 1929 के लेख apod.nasa.gov/diamond_jubilee/d_1996/hub_1929.html से )

और 70 के बजाय 500 नंबर मिल गया। फिर भी, त्रुटि 10 गुना से कम है, जो एक हिट के लिए सुरक्षित है।

डार्क एनर्जी?

आंकड़ों में आप देख सकते हैं कि रेखा केवल आरेख की शुरुआत में फिट होती है। इसके अलावा, रैखिक सन्निकटन बिल्कुल फिट नहीं है। अगले चरण के लिए, हमें ब्रह्माण्ड विज्ञान में थोड़ा गोता लगाने की आवश्यकता होगी। सबसे सरल मॉडल में, ब्रह्मांड में पदार्थ और डार्क एनर्जी (आइंस्टीन लैम्ब्डा शब्द) होते हैं, और सपाट होते हैं। ओमेगा_एम और ओमेगा_ के लिए कुछ डार्क एनर्जी से यूनिवर्स के दूसरे भाग के लिए यूनिवर्स के हिस्से को नामित करके और ओमेगा_एम + ओमेगा_ = 1 से, मैं फॉर्मूला का उपयोग करके ऑब्जेक्ट को दूरी व्यक्त कर सकता हूं (अधिक विवरण विकिपीडिया पर पढ़ा जा सकता है: [1] [२] ):

हम सहायक फ़ंक्शन E (z) का परिचय देते हैं: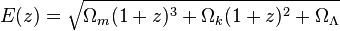

ओमेगा_के, जो यहां दिखाई देता है, ब्रह्मांड की वक्रता के लिए जिम्मेदार है। सादगी के लिए, हम इसे सपाट मानते हैं, अर्थात ओमेगा_के = 0। इसलिए, निम्न सूत्र में, हमें मध्य रेखा की आवश्यकता है:

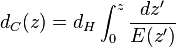मुख्य अभिन्न

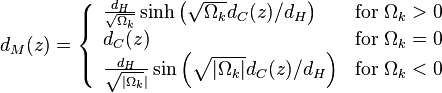अतिरिक्त कारक (1 + z), जिसका मूल समझाने के लिए बहुत लंबा है :):


अगला, हम उस कोड को लिखते हैं जो अभिन्न की गणना करता है:

 #  E_z def e_Z(z, OmegaM): OmegaL=1.0-OmegaM return (OmegaM*(1.0+z)**3+OmegaL)**(-0.5) #   scipy   import scipy.integrate as si #  def D_L(z, OmegaM): dh=4286.0 #   c/H,  H    70 // D_c=dh*si.quad(e_Z,0.0,z,args=(OmegaM))[0] return D_c*(1.0+z) #    ,       def D_L_batch(z,OmegaM,H): DL=z.copy() for i in range(len(z)): DL[i]=D_L(z[i],OmegaM,H) return DL #   plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18) #      z-  0  1.5, 100  temp_z=np.linspace(0,1.5,100) #       v- temp_v=z2v(temp_z) #         Omega_M plt.plot(D_L_batch(temp_z,0.01,70.0),temp_v,'r') plt.plot(D_L_batch(temp_z,0.27,70.0),temp_v,'g') plt.plot(D_L_batch(temp_z,0.99,70.0),temp_v,'m') plt.legend(('data',r'$\Omega_M=0.01$',r'$\Omega_M=0.27$',r'$\Omega_M=0.99$'),loc=4) 

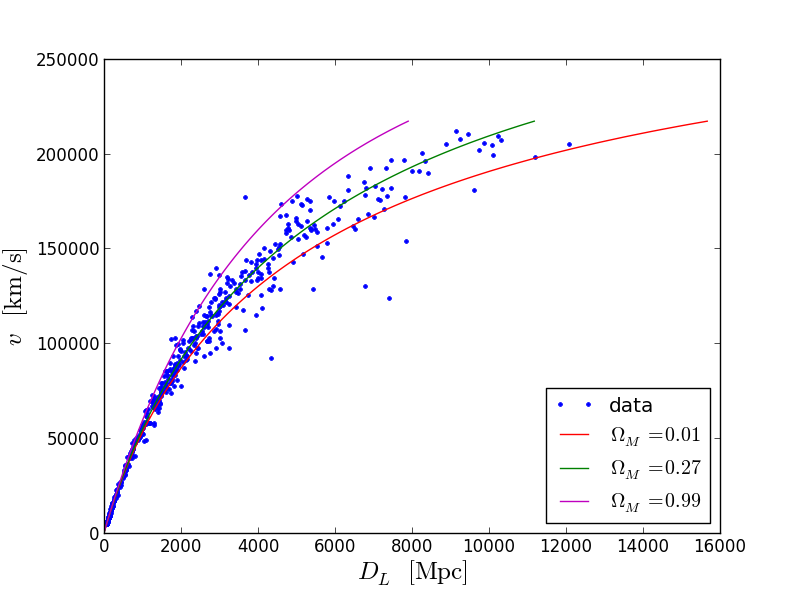
हरे रंग का वक्र डेटा को थोड़ा बेहतर बनाता है। फिर, सरलता के लिए, हम सिद्धांत को डेटा में दर्ज करने की त्रुटि के बारे में भूल जाते हैं। निष्कर्ष इस प्रकार है। डार्क एनर्जी और पदार्थ की मात्रा आज की तुलना में है (मॉडल जिसमें 100 से 1 का अनुपात डेटा में फिट नहीं होता है)। यह एक बहुत ही रोचक तथ्य है। ब्रह्मांड के बारे में ~ 70% एक प्रकार की अंधेरी ऊर्जा है, जिसकी प्रकृति हम अभी तक नहीं समझ पाए हैं। शेष ~ 30% द्रव्य भी उतना सरल नहीं है जितना लगता है। इसका केवल पांचवां हिस्सा बैरोनिक पदार्थ है (जिसमें से हम एक हैं), और बाकी डार्क मैटर है । उसके लिए, इसकी मात्रा का अनुमान किसी और समय भी लगाया जा सकता है।

खैर, हम यहाँ हैं। अंत में मैं सिर्फ इतना कहूंगा कि यह ब्रह्मांड की ज्यामिति और आयु को मापने के एकमात्र तरीके से दूर है। उनमें से कई हैं। और जो उल्लेखनीय है, वे सभी बिग बैंग सिद्धांत और विस्तारित ब्रह्मांड के पक्ष में बोलते हैं।

यीशु, सज्जनों के नाम की शुभकामनाएं! :)