🙎🏾 😊 🖕🏽 सपाट छवि के लिए मिंकोव्स्की फ्रैक्टल आयाम की गणना 😇 👩‍⚕️ 👩🏼‍🤝‍👨🏾

अच्छे दिन के पाठक। आज की पोस्ट एक सपाट छवि के भग्न आयाम के अनुमानित मूल्य की गणना करने के लिए समर्पित होगी, जो मिंकॉस्की आयाम से निकटता से संबंधित है। यह कम से कम दो कारणों से दिलचस्प है। सबसे पहले, यह पता चला है कि एक मीट्रिक अंतरिक्ष में एक बंधे हुए सेट का आयाम न केवल एक पूर्णांक, बल्कि किसी भी गैर-नकारात्मक हो सकता है। दूसरे, छवि समोच्च के आयाम का मूल्य (और यह मीट्रिक स्थान में एक सीमित सेट है) एक अच्छा संकेत है । आज की पोस्ट के हिस्से के रूप में, इस सुविधा की मजबूती के बारे में कोई शोध नहीं हुआ है, लेकिन आइए एक मामले को बिंदु पर देखें। ठीक सुई पंचर बायोप्सी छवियों के विश्लेषण से प्राप्त स्तन ट्यूमर कोशिकाओं की कई अलग-अलग विशेषताएं । बहुत सारे डेटा में 30 संकेत (टेबल फ़ील्ड) होते हैं जो घातक या सौम्य ट्यूमर के रूप में चिह्नित होते हैं, और संकेतों में से एक ट्यूमर कोशिकाओं के नाभिक का भग्न आयाम है। कटौती के तहत, आपको सेट के भग्न आयाम के अर्थ की व्याख्या मिल जाएगी, यदि संभव हो तो, इस आयाम के अनुमानित मूल्य की गणना के लिए एक एल्गोरिथ्म, c # में इसका कार्यान्वयन और चित्रों के साथ कई उदाहरण हैं। शायद आपने यह पोस्ट केवल दाईं ओर की तस्वीर के कारण खोली है, मैंने जेनिफर सेल्टर इंस्टाग्राम से इस छवि को उधार लिया है, और अंत में हम भग्न आयाम की गणना करेंगे, इसलिए जेनिफर के कहने पर। वैसे, मैं आपको पोस्ट के अंत में कुछ सवालों के जवाब देने के लिए कहना चाहूंगा।

आयामी स्वरूप

हमेशा की तरह, एल्गोरिथ्म के अर्थ को समझने के लिए, सिद्धांत में थोड़ा डुबकी लगाना आवश्यक है। विकिपीडिया हमें बताता है कि भौतिकी में आयाम (और सबसे अधिक संभावना है कि ज्यादातर लोग इस तरह से आयाम का अर्थ समझते हैं) एक वस्तु की स्थिति, या एक भौतिक प्रणाली की स्वतंत्रता की डिग्री की संख्या का वर्णन करने के लिए आवश्यक स्वतंत्र मापदंडों की संख्या है। लेकिन गणित में, चीजें थोड़ी अलग हैं, यहां हमारे पास आयामों की कई परिभाषाएं हैं, जो अक्सर कार्यक्षेत्र पर निर्भर करती हैं। सामान्य टोपोलॉजी के ढांचे के भीतर, आयाम की कई परिभाषाएं दी गई हैं, और इनमें से हम हॉसडोर्फ़ आयाम, मिंकॉस्की आयाम और भग्न आयाम में रुचि लेंगे।

शुरू करने के लिए, आइए हम उन आयामों के औपचारिक अर्थ को याद करें जो हमारे लिए सदिश स्थान में हमारे लिए सहज हैं। एक वेक्टर स्थान के आधार पर हमारा मतलब है रैखिक रूप से स्वतंत्र वैक्टर के अधिकतम सेट। हम इन वैक्टरों की संख्या को वेक्टर अंतरिक्ष के आयाम, या इसकी रैंक कहते हैं। और वेक्टर अंतरिक्ष के किसी भी तत्व को आधार वैक्टर के रैखिक संयोजन के रूप में दर्शाया जा सकता है।

हौसडॉर्फ़ आयाम

होसडॉर्फ आयाम एक वास्तविक वेक्टर अंतरिक्ष के आयाम की अवधारणा को सामान्य करता है, और एक मीट्रिक अंतरिक्ष में एक सबसेट के आयाम को निर्धारित करने का एक प्राकृतिक तरीका है। उदाहरण के लिए, एक n- आयामी के हॉसडोर्फ़ आयाम (एक वेक्टर अंतरिक्ष के अर्थ में आयाम) एकात्मक अंतरिक्ष (एक वेक्टर अंतरिक्ष का एक विशेष मामला) भी n होगा । हौसडॉर्फ आयाम का एक अच्छा गणितीय वर्णन रूसी विकिपीडिया में दिया गया है , लेकिन हमारे लिए इस आयाम के अर्थ को सहज रूप से समझना महत्वपूर्ण है। हम सेट एक्स के पूर्ण कवर का प्रतिनिधित्व करते हैं जो कि त्रिज्या की गेंदों से अधिक नहीं है, और एन (आर) द्वारा इन गेंदों की संख्या को निरूपित करते हैं।

N (r) का मान घटती r के साथ बढ़ेगा (पूर्ण कवरेज के लिए अधिक से अधिक गेंदों की आवश्यकता होगी)। एक अच्छे सेट X का हौसडॉर्फ़ आयाम एक ऐसी अनूठी संख्या d होगा जो N (r) के रूप में बढ़ेगा 1 / r ^{d के} रूप में r दृष्टिकोण शून्य होगा। उदाहरण के लिए एक अच्छा सेट विलक्षणताओं के बिना चिकनी सेट के रूप में समझा जाता है, उदाहरण के लिए। अच्छे सेटों के उदाहरण किसी भी आदर्श ज्यामितीय वस्तुएं हैं जैसे कि घन, एक गोला, और इसी तरह।

भग्न आयाम

आइए हम भग्न आयाम को निर्दिष्ट करने के एक सरल तरीके का वर्णन करते हैं, हालांकि उदाहरण के लिए मिन्कोवस्की आयाम भी भग्न आयामों में से एक है, और यह हौसडॉर्फ आयाम के साथ घनिष्ठ रूप से जुड़ा हुआ है, लेकिन बाद में उस पर और अधिक। भग्न आयाम निर्दिष्ट करने का एक सरल तरीका यहां दिया गया है:

हम कुछ डी- आयामी ज्यामितीय संरचना लेते हैं और इसके पक्षों को एम बराबर भागों में विभाजित करते हैं (अगले पुनरावृत्ति पर, हम पिछले पुनरावृत्ति में प्राप्त प्रत्येक भाग को एम भागों में विभाजित करेंगे)
प्रत्येक स्तर में पिछले स्तर के एम ^डी भागों शामिल होंगे
आइए हम निरूपित करें कि एन = एम ^डी प्राप्त भागों की संख्या निम्नानुसार है

भग्न आयाम डी के मूल्य के सूत्र की गणना करने के लिए हम निम्नलिखित परिवर्तन करते हैं:

आइए सरल उदाहरण देखें जो मैंने एकीकृत प्रणालियों पर एक बहुत ही शांत पाठ्यक्रम से सीखा है। हम एक सेगमेंट (एक आयामी आयामी सेट) लेते हैं, इसे दो समान भागों में विभाजित करते हैं, और हम प्राप्त प्रत्येक भाग के साथ भी ऐसा ही करेंगे। इस तरह हम सेट की पूरी कवरेज बनाएंगे।

यानी एम = 2 और एन = 2 , क्योंकि प्रत्येक भाग से खंड के दो नए टुकड़े उत्पन्न होते हैं, हम D की गणना करते हैं:

यदि आप खंड को 2 भागों में नहीं, बल्कि 3 में विभाजित करते हैं, तो D अभी भी 1 के बराबर होगा, क्योंकि एम = 3 और एन = 3 । यह आयाम एक अच्छे सेट के लिए हॉसडॉर्फ आयाम के साथ मेल खाता है।

आइए एक वर्ग के लिए एक समान प्रक्रिया को देखें।

हमें M = 2 और N = 4 मिलता है , क्योंकि पक्षों को 2 बराबर भागों में विभाजित करते हुए, हमें 4 नए मिलते हैं, भग्न आयाम की गणना करते हैं

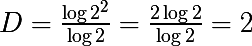
और फिर से परिणामी आयाम हॉसडॉर्फ आयाम के साथ मेल खाता है। यदि पार्टियों को 3 समान भागों में विभाजित किया जाता है, तो वही परिणाम प्राप्त किया जा सकता है, आदि।

वास्तविक वस्तुओं के अध्ययन में बेनोइट मैंडलब्रॉट ने एक स्पष्ट टिप्पणी की:

बादल क्षेत्र नहीं हैं, पहाड़ शंकु नहीं हैं, समुद्र तट वृत्त नहीं हैं, और छाल चिकनी नहीं है, और न ही बिजली सीधी रेखा में यात्रा करती है

वास्तविक दुनिया में, हम शायद ही कभी आदर्श वस्तुओं के साथ व्यवहार करते हैं, क्या होता है यदि हम एक नहीं-तो-अच्छा ज्यामितीय वस्तु पर विचार करते हैं , उदाहरण के लिए, कोक वक्र (एक छड़ी के साथ भ्रमित नहीं होना), इस तरह के सेट को बनाने के लिए एल्गोरिथ्म को याद रखें। प्रत्येक नए पुनरावृत्ति पर, वक्र का प्रत्येक टुकड़ा, जो एक सीधा खंड होता है, को तीन समान भागों में विभाजित किया जाता है, फिर बीच का टुकड़ा निकाल दिया जाता है, और इसके स्थान पर एक उल्टे अक्षर V से मिलता-जुलता एक डिज़ाइन होता है, जिसका प्रत्येक किनारा खंड के हटाए गए भाग के बराबर होता है (साथ ही शेष भी )।

दूसरे शब्दों में, एम = 3 , क्योंकि खंड को तीन समान भागों में विभाजित किया गया है, और एन = 4 , क्योंकि प्रत्येक भाग मूल के 1/4 के बराबर 4 भागों में बदल जाता है। तब अनंत पुनरावृत्ति वाले इस तरह के सेट का भग्न आयाम निम्न मूल्य के बराबर होगा:

एक अन्य उदाहरण के रूप में, आइए Sierpinski त्रिभुज को देखें

प्रत्येक पुनरावृत्ति पर, एक पक्ष को 2 भागों में विभाजित किया जाता है, अर्थात। एम = 2 , और परिणाम 3 भागों, अर्थात् है। एन = 3 , फिर

प्रश्न स्वाभाविक रूप से उठता है, यहां हमें कुछ संख्याएं मिलीं, ठीक है, आयाम भिन्नात्मक हो गया है, और इसलिए क्या? क्या इसका कोई मतलब है, या यह सिर्फ गणितीय सामान है। भिन्नात्मक आयाम का अर्थ बताने वाला कोई सख्त शब्द नहीं है, लेकिन इसकी व्याख्या कुछ सहज स्तर पर निम्न प्रकार से की जा सकती है। भग्न आयाम संवेदनशील है

वास्तविक वस्तुओं की सभी प्रकार की खामियों के कारण, जो हमें पहले से स्पष्ट और अविभाज्य ( स्रोत ) भेद करने और व्यक्त करने की अनुमति देता है ( स्रोत )

जटिल प्रणालियों के विश्लेषण पर पाठ्यक्रम में निम्नलिखित व्याख्या का उल्लेख किया गया है: भिन्नात्मक आयाम एक प्रकार का आत्म-समानता घनत्व है ।

लेकिन वास्तविक वस्तुओं की बात करते हुए, पाठक तुरंत कहेंगे, लेकिन कोच वक्र और सीरपिन्स्की त्रिकोण दोनों वास्तविकता से बहुत दूर हैं, फिर क्या किया जाना चाहिए? जैसा कि मैंने ऊपर उल्लेख किया है, भग्न आयाम की उपरोक्त परिभाषा सरल है, और कई में से एक है। आइए भग्न आयाम की अधिक जटिल परिभाषा पर चलते हैं। इस बीच, उदाहरण के लिए, रोमनस्क्यू ब्रोकोली पर एक नज़र डालें, यह वास्तविकता है।

मिन्कोवस्की आयाम

Minkowski आयाम मीट्रिक अंतरिक्ष में एक बंधे हुए सेट के भग्न आयाम को निर्दिष्ट करने के तरीकों में से एक है, इसे इस प्रकार परिभाषित किया गया है:

जहाँ N ( diameter) व्यास (के सेट की न्यूनतम संख्या है जो मूल सेट को कवर कर सकता है।

यदि सीमा मौजूद नहीं है, तो ऊपरी और निचली सीमाओं पर विचार करें और क्रमशः ऊपरी और निचले मिंकोव्स्की आयामों के बारे में बात करें। ऊपरी और निचले मिन्कोवस्की आयाम हौसडॉर्फ आयाम से निकटता से संबंधित हैं, सहजता से, आयाम निर्दिष्ट करने के तरीके से पकड़ना आसान है। आमतौर पर ये तीन आयाम मेल खाते हैं, और केवल बहुत विशिष्ट मामलों में ही इनको अलग करने का कोई मतलब नहीं है, लेकिन ये हमारे मामले नहीं हैं।

Minkowski आयाम का एक और नाम भी है - बॉक्स-गिनती आयाम , इसे निर्धारित करने के एक वैकल्पिक तरीके के कारण, जो कि इस समान आयाम की गणना करने की विधि का संकेत देता है। हम द्वि-आयामी मामले पर विचार करते हैं, हालांकि एक समान परिभाषा n-आयामी मामले पर लागू होती है। आइए हम मीट्रिक स्पेस में कुछ सीमित सेट लेते हैं, उदाहरण के लिए, एक काली-और-सफेद तस्वीर, चरण and के साथ उस पर एक समान ग्रिड खींचना और ग्रिड की उन कोशिकाओं को भरना जिनमें वांछित सेट का कम से कम एक तत्व होता है।

अगला, हम कोशिकाओं के आकार को कम करना शुरू करते हैं, अर्थात। ink , फिर Minkowski आयाम की गणना उपरोक्त सूत्र द्वारा की जाएगी, लघुगणक के अनुपात के परिवर्तन की दर की जांच। यह वाक्यांश तुरंत स्पष्ट नहीं हो सकता है, लेकिन मुझे लगता है कि सब कुछ मिन्कोवस्की आयाम के अनुमानित मूल्य की गणना करने के लिए उपयोग किए जाने वाले एल्गोरिदम को स्पष्ट करेगा।

बॉक्स-गिनती एल्गोरिथ्म

एल्गोरिथ्म निम्नानुसार है, हम डी _बीसी द्वारा Minkowski आयाम _के अनुमानित मूल्य को दर्शाते हैं। हम इस आयाम की परिभाषा लिखते हैं, सीमा को हटाते हुए, हम इसे पुनरावृत्तियों में अनुकरण करेंगे जिसमें सेल आकार बदल जाएगा।

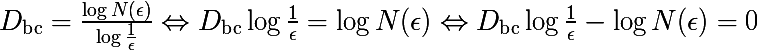
अगर हम सेल के आकार को ठीक करते हैं और डी _बीसी को अज्ञात मानते हैं, तो यह नोटिस करना आसान है कि उपरोक्त अभिव्यक्ति एक रेखा सूत्र है। हम of कोशिकाओं के विभिन्न आकारों के साथ चक्र शुरू कर सकते हैं और परिणाम रिकॉर्ड कर सकते हैं। आइए इन परिणामों को एक ग्राफ पर रखें और प्राप्त डेटा सेट के लिए एक प्रतिगमन रेखा का निर्माण करें, यह मान Minkowski भग्न आयाम का एक अनुमान होगा।

यहाँ जिस तरह से उनके भग्न आयामों के साथ वस्तुओं की सूची है ।

मुझे आशा है कि मैं प्राकृतिक आयाम के बीच के संबंध को व्यक्त करने में कामयाब रहा, और कैसे और क्यों लोग आयाम की अन्य परिभाषाओं में आए। चलो कोड पर चलते हैं, और फिर उदाहरणों के लिए।

बॉक्स-गिनती एल्गोरिथ्म, सी # कोड

मिंकोव्स्की आयाम की गणना करने के लिए, हमें दो प्रक्रियाओं की आवश्यकता होगी, हम रैखिक प्रतिगमन के साथ शुरू करेंगे। सामान्य तौर पर, रेखीय प्रतिगमन समस्या को विभिन्न तरीकों से हल किया जा सकता है, ज्यादातर अक्सर ढाल वंश विधि और कम से कम वर्गों (सामान्य समीकरण) की विधि का उपयोग करके। पहला बड़े और विस्तृत डेटा पर अच्छी तरह से काम करता है, दूसरा बड़े डेटा पर कमजोर है उलटा मैट्रिक्स की गणना करने की आवश्यकता के कारण, जिसकी चौड़ाई डेटा सरणी की चौड़ाई के बराबर है। हमारे मामले में, चौड़ाई केवल 2 है, इसलिए यह हमारा मामला है। एक वेक्टरकृत रूप में, रैखिक प्रतिगमन समाधान इस प्रकार लिखा जाता है:

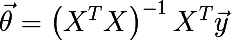
हम निम्न सूत्र द्वारा व्युत्क्रम मैट्रिक्स की तलाश करेंगे:

सामान्य समीकरण

public static double[] NormalEquations2d(double[] y, double[] x) { //x^t * x double[,] xtx = new double[2, 2]; for (int i = 0; i < x.Length; i++) { xtx[0, 1] += x[i]; xtx[0, 0] += x[i] * x[i]; } xtx[1, 0] = xtx[0, 1]; xtx[1, 1] = x.Length; //inverse double[,] xtxInv = new double[2, 2]; double d = 1/(xtx[0, 0]*xtx[1, 1] - xtx[1, 0]*xtx[0, 1]); xtxInv[0, 0] = xtx[1, 1]*d; xtxInv[0, 1] = -xtx[0, 1]*d; xtxInv[1, 0] = -xtx[1, 0]*d; xtxInv[1, 1] = xtx[0, 0]*d; //times x^t double[,] xtxInvxt = new double[2, x.Length]; for (int i = 0; i < 2; i++) { for (int j = 0; j < x.Length; j++) { xtxInvxt[i, j] = xtxInv[i, 0]*x[j] + xtxInv[i, 1]; } } //times y double[] theta = new double[2]; for (int i = 0; i < 2; i++) { for (int j = 0; j < x.Length; j++) { theta[i] += xtxInvxt[i, j]*y[j]; } } return theta; }

आउटपुट वेक्टर के शून्य तत्व में कोणीय गुणांक होता है (यह वांछित मिन्कोवस्की आयाम होगा), और अगले तत्व में ऑफसेट शामिल हैं। और वास्तव में मुख्य फ़ंक्शन जो डेटासेट लौटाता है जिसके द्वारा कोणीय गुणांक की गणना करना आवश्यक है

बॉक्स की गिनती

 /// <summary> /// Box-counting algorithm /// </summary> /// <param name="bw">black-white bitmap</param> /// <param name="startSize">initial size of square of grid</param> /// <param name="finishSize">final size of square of grid</param> /// <param name="step">step of changing of the grid</param> /// <returns>baList.Add(Math.Log(1d/b), Math.Log(a)), where b is swuare length size, a is the number of intersection of image with grid squares</returns> public static IDictionary<double, double> BowCountingDimension(BwBitmap bw, int startSize, int finishSize, int step = 1, string dataPath = "") { //length size - number of boxes IDictionary<double, double> baList = new Dictionary<double, double>(); for (int b = startSize; b <= finishSize; b += step) { int hCount = bw.Height/b; int wCount = bw.Width/b; bool[,] filledBoxes = new bool[wCount + (bw.Width > wCount*b ? 1 : 0), hCount + (bw.Height > hCount*b ? 1 : 0)]; for (int x = 0; x < bw.Width; x++) { for (int y = 0; y < bw.Height; y++) { if (bw.GetBwPixel(x, y)) { int xBox = x/b; int yBox = y/b; filledBoxes[xBox, yBox] = true; } } } int a = 0; for (int i = 0; i < filledBoxes.GetLength(0); i++) { for (int j = 0; j < filledBoxes.GetLength(1); j++) { if (filledBoxes[i, j]) { a++; } } } baList.Add(Math.Log(1d/b), Math.Log(a)); if (dataPath.Length > 0) { if (dataPath[dataPath.Length - 1] != '\\') { dataPath += '\\'; } if (Directory.Exists(dataPath)) { XBitmap bmp = new XBitmap(bw); for (int i = 0; i < filledBoxes.GetLength(0); i++) { bmp.DrawLine(i * b, 0, i * b, bmp.Height, Color.HotPink); } for (int j = 0; j < filledBoxes.GetLength(1); j++) { bmp.DrawLine(0, j * b, bmp.Width, j * b, Color.HotPink); } for (int i = 0; i < filledBoxes.GetLength(0); i++) { for (int j = 0; j < filledBoxes.GetLength(1); j++) { if (filledBoxes[i, j]) { bmp.FillRectangle(i * b, j * b, i * b + b, j * b + b, Color.Red, 2); } } } bmp.ConvertToNativeBitmap().Save(dataPath + b + ".bmp"); } } Logger.Instance.Log("BoxCounting: b is " + b + " of " + finishSize); } if (dataPath.Length > 0) { using (StreamWriter sw = new StreamWriter(dataPath + "ba.csv")) { sw.WriteLine("NumberOfBoxes,LengthOfSideInv"); foreach (double bInv in baList.Keys) { sw.WriteLine(baList[bInv] + "," + bInv); } sw.Close(); } } return baList; }

यह केवल दो प्रक्रियाओं को जोड़ने के लिए बना हुआ है:

 IDictionary<double, double> baList = BowCountingDimension(bwContour, 5, 100, 1, dir + "boxing\\"); double[] y = new double[baList.Count]; double[] x = new double[baList.Count]; int c = 0; foreach (double key in baList.Keys) { y[c] = baList[key]; x[c] = key; c++; } double[] theta = NormalEquations2d(y, x);

उदाहरण

पत्र

सुविधाओं के बिना एक साधारण छवि पर विचार करें, अर्थात चिकने किनारों के साथ। कंप्यूटर दृष्टि में, यह अक्सर पूरी छवि नहीं होती है जिसका विश्लेषण किया जाता है, लेकिन इसकी रूपरेखा।

इकाई क्षेत्र में भग्न आयाम हमें बताता है कि आंकड़ा वास्तव में सुविधाओं के बिना है, और काफी चिकनी है।

कोच वक्र

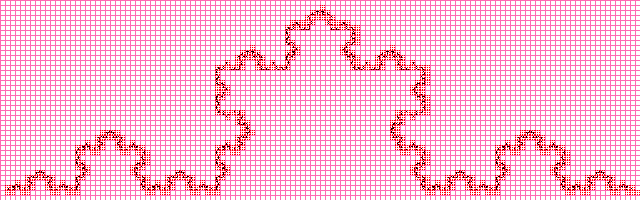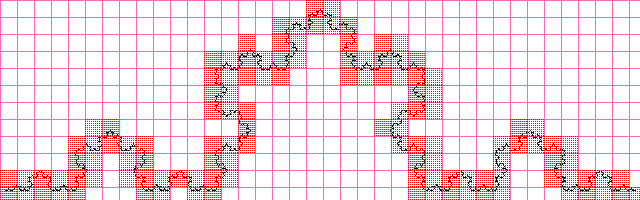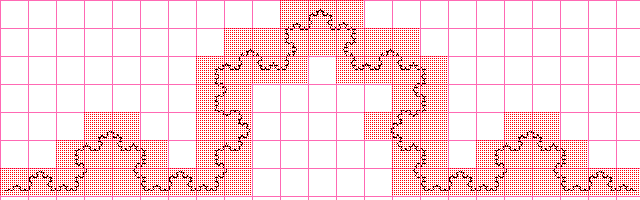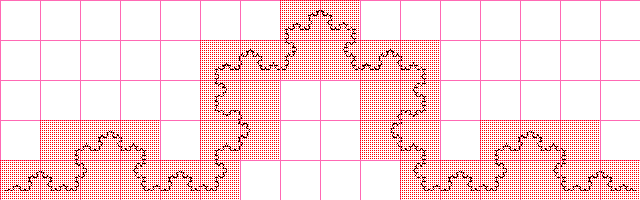
मूल्य लगभग समान रूप से निकला जब भग्न आयाम को विश्लेषणात्मक रूप से गणना करते हैं, तो यह स्पष्ट है कि बढ़ती छवि रिज़ॉल्यूशन के साथ, अनुमानित मूल्य विश्लेषणात्मक रूप से गणना की जाएगी।

JanSetler

रूस का नक्शा

कुछ और बीहड़ लें, जैसे कि हमारे देश का नक्शा।

यह पता चला है कि पुजारी जेनिफर रूस के समोच्च की तुलना में थोड़ा अधिक दिलचस्प है, ठीक है, आप क्या कर सकते हैं।

भग्न

भग्न के लिए आयाम मान में काफी भिन्नता होगी? आइए इसे देखें। हम जूलिया सेट में से एक पर विचार करते हैं, अधिक सटीक रूप से, इसकी सीमा। मुझे GIF को काटना पड़ा, क्योंकि कार्यक्रम उच्च संकल्प के साथ सामना नहीं कर सका, और स्केलिंग ने ग्रिड को मिटा दिया।

जैसा कि आप देख सकते हैं, पुजारी जेनिफर की तुलना में भग्न अधिक दिलचस्प है।

संदर्भ

आप ऊपर दिए गए लिंक पर सभी जानकारी पा सकते हैं, अंत में मैं केवल दो पाठ्यक्रमों के बारे में दोहराऊंगा, दूसरा, वैसे, केवल कुछ दिनों पहले शुरू हुआ था, इसलिए मैं सभी को सलाह देता हूं।

एक बार जब मैंने हब्रिंस के मंत्रियों को एक पत्र भेजा, तो मुझे एक मशीन लर्निंग हब बनाने के लिए कहा, तो मुझे निम्नलिखित उत्तर मिला: "अगर 15-20 पोस्ट हैं जो बस इस हब में होनी चाहिए, तो हम इसके बारे में सोचेंगे।" सामान्य तौर पर, लंबे समय से इस तरह के 15-20 से अधिक पद पहले से ही हैं, मेरे पास केवल उनमें से कम से कम 10 हैं। मैं समझता हूं कि प्रशासन पर राजनीति के साथ हब के साथ अधिक कब्जा है, लेकिन हम वास्तव में महत्वपूर्ण हब पर उनका ध्यान आकर्षित करने की कोशिश कर सकते हैं।

सपाट छवि के लिए मिंकोव्स्की फ्रैक्टल आयाम की गणना