✍🏽 👩🏿‍🤝‍👨🏼 👨🏻 Fuzzy c-PHP में फजी क्लस्टरिंग एल्गोरिदम का मतलब है 🖐🏼 📏 🙍🏾

शुभ दिन।

नीचे दिए गए पोस्ट और कोड न केवल व्यावसायिक उद्देश्यों के लिए एल्गोरिथ्म का उपयोग करने के लिए हैं, बल्कि यह समझने के लिए कि फ़ज़ी सी-मतलब एल्गोरिथ्म कैसे काम करता है और संभवतः, इस एल्गोरिथ्म को अन्य भाषाओं में लागू करने या दिए गए कोड और इसके आगे सुधार करने के लिए एक प्रेरणा देता है। कार्य उद्देश्यों के लिए उपयोग करें।

सामान्य जानकारी

सबसे पहले, यह बहुत जल्दी से यह बताने लायक है कि फुलस्टेयरिंग क्या है और फजी क्लस्टरिंग के बारे में क्या खास है।

क्लस्टरिंग, जैसा कि विक्षनरी शब्द का वर्णन है,

समूहन, वस्तुओं के समुच्चय को असमान उपसमूह में विभाजित करना, समान वस्तुओं से मिलकर क्लस्टर

यह परिभाषा काफी समझ में आती है और मुझे लगता है कि इसे अतिरिक्त स्पष्टीकरण की आवश्यकता नहीं है।

फिर "फजी क्लस्टरिंग" क्या है?
फजी क्लस्टरिंग साधारण क्लस्टरिंग से अलग होती है, जो क्लस्टर किए गए ऑब्जेक्ट एक निश्चित संबद्धता के साथ एक विशिष्ट क्लस्टर से संबंधित होते हैं, और स्पष्ट रूप से नहीं, जैसा कि पारंपरिक क्लस्टरिंग के साथ होता है। उदाहरण के लिए, फजी क्लस्टरिंग के साथ, ऑब्जेक्ट A का संबंध सदस्यता K के साथ क्लस्टर K1 से है, सदस्यता K4 के क्लस्टर क्लस्टर K2 से है, और सदस्यता K6 के साथ क्लस्टर K3 से है। साधारण (स्पष्ट) क्लस्टरिंग में, ऑब्जेक्ट A को क्लस्टर K1 में सौंपा जाएगा।

आप इस हब में इस एल्गोरिथ्म का गणितीय विवरण पा सकते हैं।

PHP में फ़ज़ी सी-साधन को लागू करना।

आइए एल्गोरिदम के कार्यान्वयन के लिए सीधे चलते हैं। ऐसा करने के लिए, मैं अधिक या कम वास्तविक उदाहरण पर कार्यान्वयन पर विचार करूंगा। इस तरह का एक उदाहरण निम्नलिखित हो सकता है - चलो उनके आरजीबी मूल्य से क्लस्टर पिक्सेल, अर्थात्। वास्तव में रंग में। नतीजतन, हम एल्गोरिथ्म के निष्पादन का परिणाम स्पष्ट रूप से देख सकते हैं।

नीचे एल्गोरिथ्म का कोड है, जिसका मैं नीचे और अधिक विस्तार से विश्लेषण करूंगा।

फजी सी-मतलब एल्गोरिथ्म को उनके RGB मान द्वारा क्लस्टरिंग बिंदुओं के लिए लागू करना

define('EPLSION', 0.1); define('MAX_EXECUTION_CYCLES', 150); define('POINTS_COUNT', 100); define('CLUSTERS_NUM', 3); define('FUZZ', 1.5); class Point { public $r; public $g; public $b; } // Random values 0 - 1 function random_float ($min,$max) { return ($min+lcg_value()*(abs($max-$min))); } // Fuzzy C Means Algorithm function distributeOverMatrixU($arr, $m, &$centers) { $centers = generateRandomPoints(CLUSTERS_NUM); $MatrixU = fillUMatrix(count($arr), count($centers)); $previousDecisionValue = 0; $currentDecisionValue = 1; for($a = 0; $a < MAX_EXECUTION_CYCLES && (abs($previousDecisionValue - $currentDecisionValue) > EPLSION); $a++){ $previousDecisionValue = $currentDecisionValue; $centers = calculateCenters($MatrixU, $m, $arr); foreach($MatrixU as $key=>&$uRow){ foreach($uRow as $clusterIndex=>&$u){ $distance = evklidDistance3D($arr[$key], $centers[$clusterIndex]); $u = prepareU($distance, $m); } $uRow = normalizeUMatrixRow($uRow); } $currentDecisionValue = calculateDecisionFunction($arr, $centers, $MatrixU); } return $MatrixU; } function fillUMatrix($pointsCount, $clustersCount) { $MatrixU = array(); for($i=0; $i<$pointsCount; $i++){ $MatrixU[$i] = array(); for($j=0; $j<$clustersCount; $j++){ $MatrixU[$i][$j] = random_float(0, 1); } $MatrixU[$i] = normalizeUMatrixRow($MatrixU[$i]); } return $MatrixU; } function calculateCenters($MatrixU, $m, $points) { $MatrixCentroids = array(); for($clusterIndex=0; $clusterIndex < CLUSTERS_NUM; $clusterIndex++){ $tempAr = 0; $tempBr = 0; $tempAg = 0; $tempBg = 0; $tempAb = 0; $tempBb = 0; foreach($MatrixU as $key=>$uRow){ $tempAr += pow($uRow[$clusterIndex],$m); $tempBr += pow($uRow[$clusterIndex],$m) * $points[$key]->r; $tempAg += pow($uRow[$clusterIndex],$m); $tempBg += pow($uRow[$clusterIndex],$m) * $points[$key]->g; $tempAb += pow($uRow[$clusterIndex],$m); $tempBb += pow($uRow[$clusterIndex],$m) * $points[$key]->b; } $MatrixCentroids[$clusterIndex] = new Point(); $MatrixCentroids[$clusterIndex]->r = $tempBr / $tempAr; $MatrixCentroids[$clusterIndex]->g = $tempBg / $tempAg; $MatrixCentroids[$clusterIndex]->b = $tempBb / $tempAb; } return $MatrixCentroids; } function calculateDecisionFunction($MatrixPointX, $MatrixCentroids, $MatrixU) { $sum = 0; foreach($MatrixU as $index=>$uRow){ foreach($uRow as $clusterIndex=>$u){ $sum += $u * evklidDistance3D($MatrixCentroids[$clusterIndex], $MatrixPointX[$index]); } } return $sum; } function evklidDistance3D($pointA, $pointB) { $distance1 = pow(($pointA->r - $pointB->r),2); $distance2 = pow(($pointA->g - $pointB->g),2); $distance3 = pow(($pointA->b - $pointB->b),2); $distance = $distance1 + $distance2 + $distance3; return sqrt($distance); } function normalizeUMatrixRow($MatrixURow) { $sum = 0; foreach($MatrixURow as $u){ $sum += $u; } foreach($MatrixURow as &$u){ $u = $u/$sum; } return $MatrixURow; } function prepareU($distance, $m) { return pow(1/$distance , 2/($m-1)); } function generateRandomPoints($count){ $points = array_fill(0, $count, false); array_walk($points, function(&$value, $key){ $value = new Point(); $value->r = rand(20, 235); $value->g = rand(20, 235); $value->b = rand(20, 235); }); return $points; } $points = generateRandomPoints(POINTS_COUNT); $centers = array(); $matrixU = distributeOverMatrixU($points, FUZZ, $centers);

हम एक फ़ंक्शन के साथ एल्गोरिथ्म पर विचार करना शुरू करते हैं जो वास्तव में क्लस्टरिंग एल्गोरिदम को खुद लॉन्च करता है - distributeOverMatrixU यू
इसके लिए इनपुट पैरामीटर्स क्लस्टर किए गए ऑब्जेक्ट्स की एक सरणी (हमारे मामले में, क्लास पॉइंट की ऑब्जेक्ट्स वाली एक बेतरतीब ढंग से भरी हुई एरे) और अनिश्चितता गुणांक हैं। वापसी मूल्य सदस्यता मैट्रिक्स है। centers पैरामीटर को / in / out फ़ंक्शन में भी जोड़ा गया था, जिसमें एल्गोरिथ्म निष्पादित होने के बाद, हमारे क्लस्टर के केंद्र होंगे।

नए क्लस्टर केंद्र खोजने और सदस्यता मैट्रिक्स को पुनर्गठित करने के चरण स्थिरांक MAX_EXECUTION_CYCLES और EPSILON द्वारा सीमित हैं, जहां MAX_EXECUTION_CYCLES - चरणों की संख्या सीमित करता है, EPSILON सदस्यता मैट्रिक्स को खोजने की सटीकता को सीमित करता है।

एल्गोरिथम का प्रत्येक चरण निम्नानुसार है:
1) फ़ंक्शन calculateCenters का उपयोग करके समूहों के केंद्रों की calculateCenters
2) फिर प्रत्येक ऑब्जेक्ट के लिए हम प्रत्येक क्लस्टर के केंद्र के लिए यूक्लिडियन दूरी की गणना करते हैं (फ़ंक्शन evklidDistance3D - हमारे साथ 3-आयामी स्थान)
3) किसी दिए गए ऑब्जेक्ट के लिए सदस्यता गुणांक u गणना करें ( prepareU फ़ंक्शन)
4) हम किसी दिए गए ऑब्जेक्ट के लिए गुणांक u को सामान्य करते हैं (फ़ंक्शन normalizeUMatrixRow )
5) निर्णायक फ़ंक्शन के मूल्य की गणना करें ( calculateDecisionFunction फ़ंक्शन)
6) फिर निर्णायक फ़ंक्शन के वर्तमान मूल्य की तुलना उसके पिछले मूल्य से की जाती है, और यदि उनका अंतर EPSILON सेट से कम है, तो एल्गोरिथ्म काम करना बंद कर देता है।

अब प्रत्येक चरण के बारे में थोड़ा और अधिक:
1) केंद्रों की गणना निम्नलिखित सूत्र के अनुसार की जाती है

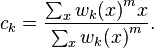
जहां wk (x) सदस्यता गुणांक है, m अनिश्चितता गुणांक है, x ऑब्जेक्ट है (एल्गोरिथम में ही, घटक R, G, B x के रूप में कार्य करता है)

2) हम 3 मापों के लिए यूक्लिडियन दूरी की गणना करते हैं, अर्थात। सूत्र इस प्रकार है:
r = sqrt((r2-r1)^2 + (g2-g1)^2 + (b2-b1)^2);
जहाँ r, g, b RGB के घटक हैं

3) सदस्यता गुणांक की गणना सूत्र द्वारा की जाती है
u = (1/d)^(2/(m-1)) ,
जहाँ घ ऑब्जेक्ट के क्लस्टर के केंद्र से दूरी है, एम अनिश्चितता गुणांक है।

4) सभी ऑब्जेक्ट संबद्धता गुणांक के सामान्यीकरण - हम गुणांक को बदलते हैं ताकि कुल में वे 1 दें, अर्थात। वास्तव में इस ऑब्जेक्ट के सभी गुणांक के योग से प्रत्येक गुणांक को विभाजित करते हैं

5) निर्णायक कार्य सदस्यता गुणांक द्वारा गुणा किए गए क्लस्टर के प्रत्येक केंद्र के लिए प्रत्येक वस्तु की सभी यूक्लिडियन दूरी का योग देता है।

6) मोडुलो निर्णय फ़ंक्शन के पिछले और वर्तमान मूल्य को घटाता है, और अगर यह अंतर EPSILON से कम है, तो एल्गोरिथ्म बंद हो जाता है और पाया सदस्यता मैट्रिक्स वापस आ जाता है।

अंत में, मैं एल्गोरिथ्म के परिणाम दिखाने वाले कुछ स्क्रीनशॉट जोड़ना चाहूंगा।
यह उन आंकड़ों में देखा जा सकता है कि एल्गोरिथ्म ने सही तरीके से काम किया और हम समान समूहों में रंग के समान अंक प्रदान करते हैं।

एल्गोरिदम प्रदर्शन

इस प्रकार, मैंने आपको फ़ज़ी सी-मतलब फ़ज़ी क्लस्टरिंग एल्गोरिदम का मूल कार्यान्वयन प्रस्तुत किया। मुझे आशा है कि वह आपके लिए उपयोगी होगी।
आपका ध्यान देने के लिए धन्यवाद।

Fuzzy c-PHP में फजी क्लस्टरिंग एल्गोरिदम का मतलब है

सामान्य जानकारी

PHP में फ़ज़ी सी-साधन को लागू करना।

More articles: