समान रूप से वितरित एक समान रूप से वितरित यादृच्छिक चर में परिवर्तित करें

इस प्रश्न का लंबे समय तक विस्तार से अध्ययन किया गया है, और ध्रुवीय निर्देशांक की सबसे व्यापक रूप से इस्तेमाल की जाने वाली विधि का प्रस्ताव 1958 में जॉर्ज बॉक्सिंग, मर्विन मुलर और जॉर्ज मार्साग्लिया ने किया था। यह विधि आपको 0 की गणितीय अपेक्षा के साथ सामान्य रूप से वितरित यादृच्छिक चर की एक जोड़ी प्राप्त करने की अनुमति देती है और 1 का एक प्रकार इस प्रकार है:

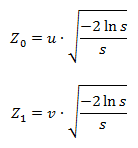
जहां Z ₀ और Z ₁ वांछित मान हैं, s = u ² + v ² , और u और v समान रूप से अंतराल (-1, 1) पर वितरित किए गए हैं, इसलिए चुना गया है कि शर्त 0 <s 1 संतुष्ट है।
कई लोग बिना सोचे समझे इन फॉर्मूलों का इस्तेमाल भी करते हैं और कई लोग अपने अस्तित्व पर संदेह भी नहीं करते हैं, क्योंकि वे तैयार किए गए कार्यान्वयन का उपयोग करते हैं। लेकिन ऐसे लोग हैं जिनके पास सवाल है: “यह सूत्र कहाँ से आया है? और एक बार में कुछ मात्रा में क्यों मिलता है? " आगे, मैं इन सवालों का स्पष्ट जवाब देने की कोशिश करूंगा।


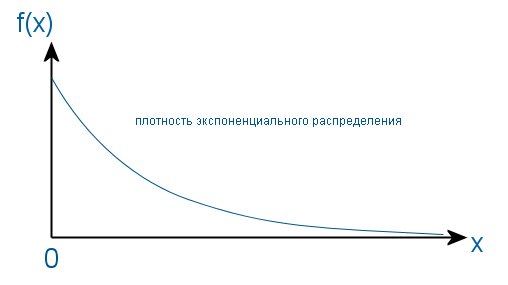
सबसे पहले, मैं आपको याद दिलाता हूं कि संभाव्यता घनत्व, यादृच्छिक चर का वितरण कार्य और व्युत्क्रम फ़ंक्शन क्या हैं। मान लें कि एक निश्चित यादृच्छिक चर है जिसका वितरण घनत्व फ़ंक्शन f (x) द्वारा दिया गया है, जिसमें निम्न रूप हैं:



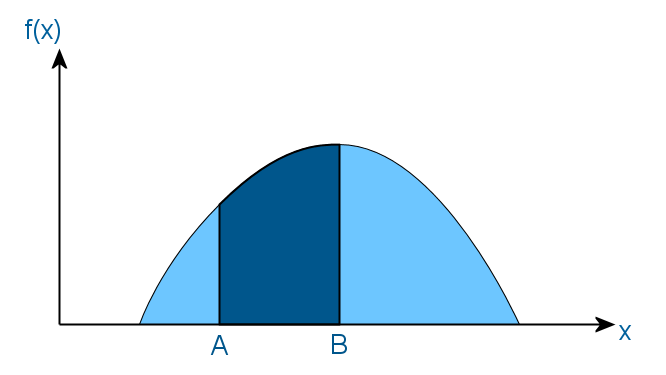
इसका मतलब यह है कि इस यादृच्छिक चर का मान अंतराल (ए, बी) में है, यह शेविंग क्षेत्र के क्षेत्र के बराबर है। और परिणामस्वरूप, पूरे छायांकित क्षेत्र का क्षेत्र एकता के बराबर होना चाहिए, क्योंकि किसी भी मामले में, यादृच्छिक चर का मान फ़ंक्शन f की परिभाषा के क्षेत्र में आता है।
एक यादृच्छिक चर का वितरण कार्य घनत्व फ़ंक्शन का एक अभिन्न अंग है। और इस मामले में, इसका अनुमानित रूप इस प्रकार होगा:



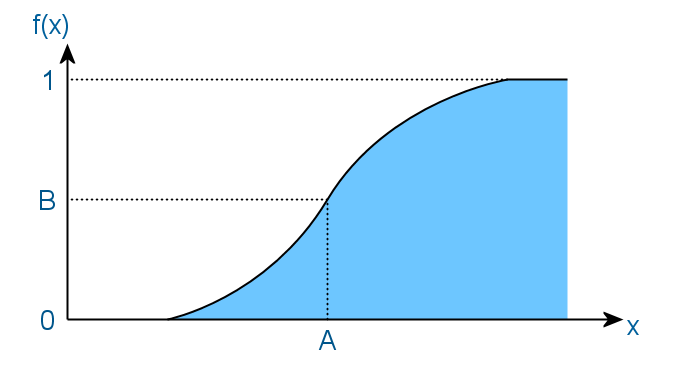
यहाँ मुद्दा यह है कि यादृच्छिक चर का मान A के साथ प्रायिकता B से कम होगा। परिणामस्वरूप, फ़ंक्शन कभी कम नहीं होता है, और इसके मान अंतराल में निहित होते हैं [0, 1]।

उलटा फ़ंक्शन एक फ़ंक्शन है जो मूल फ़ंक्शन के तर्क को वापस करता है यदि मूल फ़ंक्शन का मान इसे पास किया जाता है। उदाहरण के लिए, फ़ंक्शन x ^{2 के लिए} , रूट निष्कर्षण फ़ंक्शन व्युत्क्रम होगा, पाप (x) के लिए यह आर्क्सिन (x), आदि है।

चूंकि आउटपुट में अधिकांश छद्म आयामी संख्या जनरेटर केवल एक समान वितरण देते हैं, इसलिए अक्सर इसे किसी अन्य में परिवर्तित करना आवश्यक हो जाता है। इस मामले में, सामान्य गाऊसी में:



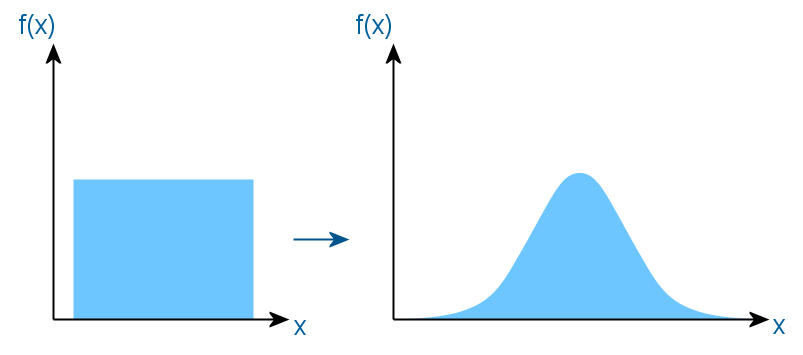
एक समान वितरण को किसी अन्य में परिवर्तित करने के सभी तरीकों का आधार उलटा परिवर्तन विधि है। यह निम्नानुसार काम करता है। एक फ़ंक्शन पाया जाता है जो आवश्यक वितरण के फ़ंक्शन के विपरीत होता है, और एक यादृच्छिक चर को समान रूप से अंतराल (0, 1) पर वितरित किया जाता है, इसे एक तर्क के रूप में स्थानांतरित किया जाता है। आउटपुट पर, हम आवश्यक वितरण के साथ मूल्य प्राप्त करते हैं। स्पष्टता के लिए, मैं निम्नलिखित चित्र उद्धृत करता हूं।



इस प्रकार, समान खंड नए वितरण के अनुसार स्मीयर किया जाता है, उलटा फ़ंक्शन के माध्यम से अन्य अक्ष पर प्रोजेक्ट करता है। लेकिन समस्या यह है कि गाऊसी वितरण के घनत्व का अभिन्न गणना करना आसान नहीं है, इसलिए उपरोक्त वैज्ञानिकों को धोखा देना पड़ा।

एक ची-स्क्वायर डिस्ट्रीब्यूशन (पियर्सन डिस्ट्रीब्यूशन) है, जो कि k इंडिपेंडेंट नॉर्मल रैंडम वैरिएबल के स्क्वेयर के योग का डिस्ट्रीब्यूशन है। और मामले में जब k = 2, यह वितरण घातीय है।



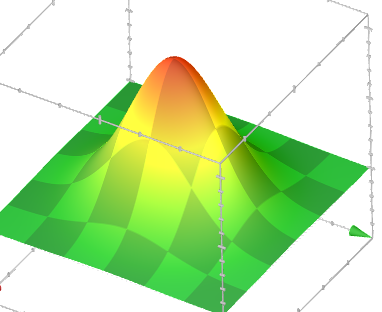
इसका मतलब यह है कि यदि एक आयताकार निर्देशांक प्रणाली के एक बिंदु में यादृच्छिक X और Y निर्देशांक सामान्य रूप से वितरित किए जाते हैं, तो इन निर्देशांक को ध्रुवीय प्रणाली (r, θ) में स्थानांतरित करने के बाद, त्रिज्या का एक वर्ग (मूल से बिंदु की दूरी) को घातीय रूप से वितरित किया जाएगा, चूंकि त्रिज्या का वर्ग निर्देशांक के वर्गों का योग है (पाइथागोरस के कानून के अनुसार)। विमान पर ऐसे बिंदुओं का वितरण घनत्व निम्नानुसार होगा:



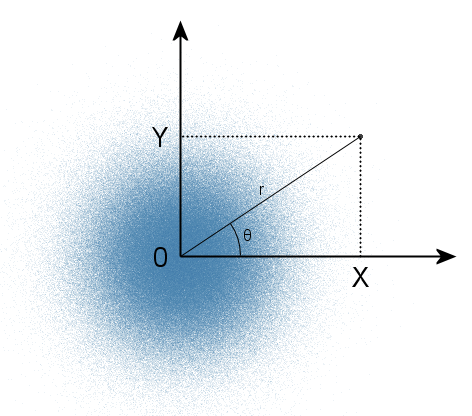
चूंकि यह सभी दिशाओं में बराबर है, कोण π 0 से 2π तक की सीमा में एक समान वितरण होगा। यह वाक्य भी सत्य है: यदि आप दो स्वतंत्र यादृच्छिक चर (समान रूप से वितरित एक कोण और एक घातीय वितरित किए गए कोण) का उपयोग करके ध्रुवीय समन्वय प्रणाली में एक बिंदु निर्दिष्ट करते हैं, तो इस बिंदु के आयताकार निर्देशांक सामान्य सामान्य यादृच्छिक यादृच्छिक चर होंगे। और पहले से ही एक ही व्युत्क्रम परिवर्तन विधि का उपयोग करके एक समान से एक घातीय वितरण प्राप्त करना बहुत आसान है। यह ध्रुवीय बॉक्स-मुलर विधि का सार है।
अब हम सूत्र निकालते हैं।

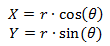
(1)

आर और obtain प्राप्त करने के लिए, हमें अंतराल (0, 1) पर समान रूप से वितरित दो यादृच्छिक चर उत्पन्न करने की आवश्यकता है (आइए हम उन्हें यू और वी कहते हैं), जिनमें से एक का वितरण (कहते हैं v) त्रिज्या प्राप्त करने के लिए घातीय में परिवर्तित किया जाना चाहिए। घातांक वितरण समारोह निम्नानुसार है:



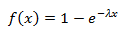
इसके विपरीत कार्य करें:



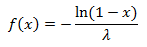
चूंकि समान वितरण सममित है, इसी तरह, परिवर्तन फ़ंक्शन के साथ काम करेगा



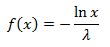
यह ची-वर्ग वितरण सूत्र से निम्नानुसार है कि λ = 0.5। हम इस फ़ंक्शन में λ, v को प्रतिस्थापित करते हैं और त्रिज्या के वर्ग को प्राप्त करते हैं, और फिर खुद त्रिज्या:



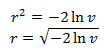
हम इकाई खंड को 2 the तक खींचकर कोण प्राप्त करते हैं:



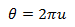
अब हम r और θ को सूत्र (1) में प्रतिस्थापित करते हैं और प्राप्त करते हैं:

(2)

ये सूत्र उपयोग करने के लिए तैयार हैं। X और Y स्वतंत्र और सामान्य रूप से 1 के विचरण के साथ वितरित किए जाएंगे और 0. की गणितीय अपेक्षा। अन्य विशेषताओं के साथ एक वितरण प्राप्त करने के लिए, बस मानक विचलन द्वारा फ़ंक्शन के परिणाम को गुणा करें और गणितीय अपेक्षा जोड़ें।
लेकिन कोण को सीधे नहीं, बल्कि सर्कल में एक यादृच्छिक बिंदु के आयताकार निर्देशांक के माध्यम से त्रिकोणमितीय कार्यों से छुटकारा पाने का अवसर है। फिर इन निर्देशांक के माध्यम से त्रिज्या वेक्टर की लंबाई की गणना करना संभव होगा, और फिर क्रमशः एक्स और वाई को विभाजित करके कोसाइन और साइन को ढूंढें। यह कैसे और क्यों काम करता है?
इकाई त्रिज्या में समान रूप से वितरित इकाई से एक यादृच्छिक बिंदु चुनें और अक्षर s द्वारा इस बिंदु की त्रिज्या वेक्टर की लंबाई के वर्ग को निरूपित करें:



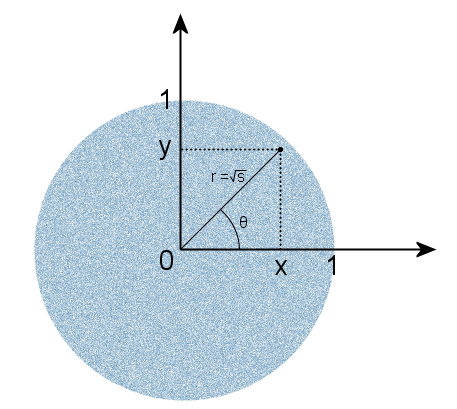
विकल्प यादृच्छिक आयताकार निर्देशांक x और y सेट करके बनाया गया है, समान रूप से अंतराल (-1, 1) में वितरित किया गया है, और उन बिंदुओं को त्यागने के लिए जो सर्कल से संबंधित नहीं हैं, साथ ही एक केंद्रीय बिंदु जिस पर त्रिज्या वेक्टर कोण परिभाषित नहीं है। यही है, शर्त s <s १ संतुष्ट होना चाहिए। फिर, जैसा कि विमान पर गौसियन वितरण के साथ होता है, कोण, समान रूप से वितरित किया जाएगा। यह स्पष्ट है - प्रत्येक दिशा में अंकों की संख्या समान है, जिसका अर्थ है कि प्रत्येक कोण समान रूप से संभावित है। लेकिन एक कम स्पष्ट तथ्य है - s का एक समान वितरण भी होगा। परिणामी s और resulting एक दूसरे से स्वतंत्र होंगे। इसलिए, हम तीसरे यादृच्छिक चर को उत्पन्न किए बिना एक घातांक वितरण प्राप्त करने के लिए s के मूल्य का उपयोग कर सकते हैं। अब हम v के बजाय सूत्र (2) में स्थानापन्न करते हैं, और त्रिकोणमितीय कार्यों के बजाय, त्रिज्या वेक्टर की लंबाई द्वारा समन्वय को विभाजित करके उनकी गणना करते हैं, जो इस मामले में है:



हमें सूत्र मिलते हैं, जैसे कि लेख की शुरुआत में। इस पद्धति का नुकसान उन बिंदुओं की अस्वीकृति है जो सर्कल में शामिल नहीं हैं। यही है, उत्पन्न यादृच्छिक चर के केवल 78.5% का उपयोग। पुराने कंप्यूटरों पर, त्रिकोणमितीय कार्यों की अनुपस्थिति ने अभी भी बहुत अच्छा लाभ दिया। अब, जब एक प्रोसेसर कमांड तत्काल साइन और कोसाइन दोनों की गणना करता है, मुझे लगता है कि ये विधियां अभी भी प्रतिस्पर्धा कर सकती हैं।

व्यक्तिगत रूप से, मेरे दो और प्रश्न हैं:

• क्यों समान रूप से वितरित किया गया है?
• घातीय रूप से वितरित दो सामान्य यादृच्छिक चर के वर्गों का योग क्यों है?

चूंकि s त्रिज्या का वर्ग है (सरलता के लिए, त्रिज्या I त्रिज्या वेक्टर की लंबाई को एक यादृच्छिक बिंदु की स्थिति निर्धारित करता है), हम पहले पता लगाते हैं कि त्रिज्या कैसे वितरित की जाती है। चूंकि सर्कल समान रूप से भरा हुआ है, इसलिए यह स्पष्ट है कि त्रिज्या r के साथ बिंदुओं की संख्या एक त्रिज्या r की परिधि के समानुपाती है। और परिधि त्रिज्या के आनुपातिक है। इसका मतलब है कि त्रिज्या वितरण घनत्व सर्कल के केंद्र से इसके किनारों तक समान रूप से बढ़ता है। और घनत्व फ़ंक्शन में अंतराल (0, 1) पर फॉर्म f (x) = 2x है। गुणांक 2 ताकि ग्राफ के तहत क्षेत्र एक के बराबर हो। जब इस तरह का घनत्व बढ़ जाता है, तो यह एक समान हो जाता है। चूंकि सैद्धांतिक रूप से इस मामले में, इसके लिए परिवर्तन फ़ंक्शन (यानी, ² एक्स से) के व्युत्पन्न द्वारा घनत्व फ़ंक्शन को विभाजित करना आवश्यक है। और नेत्रहीन इस तरह होता है:



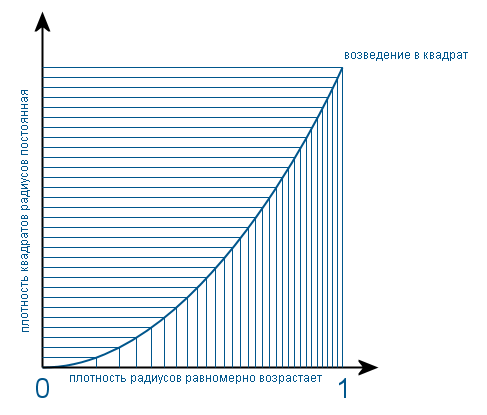
यदि एक समान परिवर्तन एक सामान्य यादृच्छिक चर के लिए किया जाता है, तो इसके वर्ग का घनत्व फ़ंक्शन एक हाइपरबोला के समान होगा। और सामान्य यादृच्छिक चर के दो वर्गों के अलावा पहले से ही दोहरे एकीकरण के साथ जुड़ी एक बहुत अधिक जटिल प्रक्रिया है। और तथ्य यह है कि परिणाम एक घातीय वितरण है, मुझे व्यक्तिगत रूप से एक व्यावहारिक विधि के साथ यहां जांचना होगा या एक स्वयंसिद्ध के रूप में स्वीकार करना होगा। और कौन परवाह करता है, मैं अपने आप को विषय के साथ परिचित करने का प्रस्ताव करता हूं, इन पुस्तकों से ज्ञान पर आरेखण:

• वेंटजेल ई.एस. संभाव्यता सिद्धांत
• नट डी.ई. प्रोग्रामिंग की कला, खंड 2

अंत में, मैं जावास्क्रिप्ट में सामान्य रूप से वितरित यादृच्छिक संख्याओं के जनरेटर के कार्यान्वयन का एक उदाहरण दूंगा:

function Gauss() { var ready = false; var second = 0.0; this.next = function(mean, dev) { mean = mean == undefined ? 0.0 : mean; dev = dev == undefined ? 1.0 : dev; if (this.ready) { this.ready = false; return this.second * dev + mean; } else { var u, v, s; do { u = 2.0 * Math.random() - 1.0; v = 2.0 * Math.random() - 1.0; s = u * u + v * v; } while (s > 1.0 || s == 0.0); var r = Math.sqrt(-2.0 * Math.log(s) / s); this.second = r * u; this.ready = true; return r * v * dev + mean; } }; } g = new Gauss(); //   a = g.next(); //         b = g.next(); //   c = g.next(); //          

माध्य (माध्य) और देव (मानक विचलन) पैरामीटर वैकल्पिक हैं। मैं इस तथ्य पर आपका ध्यान आकर्षित करता हूं कि लघुगणक प्राकृतिक है।