कुज़नेत्सोविन ने हाल ही में अर्थशास्त्र में समय श्रृंखला का विश्लेषण करने के लिए पायथन का उपयोग करने पर एक
पोस्ट किया। अर्थमिति के "वर्कहॉर्स" को मॉडल के रूप में चुना गया था - ARIMA, शायद अस्थायी डेटा के लिए सबसे आम मॉडल में से एक। इसी समय, एआरआईएमए जैसे मॉडल का मुख्य नुकसान यह है कि वे गैर-स्थिर श्रृंखला के साथ काम करने के लिए उपयुक्त नहीं हैं। उदाहरण के लिए, यदि कोई प्रवृत्ति या मौसमी डेटा में मौजूद है, तो गणितीय अपेक्षाओं के श्रृंखला के विभिन्न भागों में अलग-अलग अर्थ होंगे -
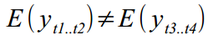
यह अच्छा नहीं है। इससे बचने के लिए, ARIMA का स्रोत डेटा के साथ काम करने का इरादा नहीं है, लेकिन उनके अंतर के साथ (तथाकथित अंतर - "एक अंतर लेने से")। सब कुछ ठीक हो जाएगा, लेकिन यहां दो समस्याएं उत्पन्न होती हैं - (ए) हम श्रृंखला के अंतर को लेते हुए महत्वपूर्ण जानकारी खो सकते हैं, और (बी) यह अवसर इसके घटक घटकों - प्रवृत्ति, चक्र, आदि में डेटा की एक श्रृंखला को विघटित करने से चूक जाता है। इसलिए, इस लेख में मैं विश्लेषण का एक वैकल्पिक तरीका देना चाहूंगा - स्टेट स्पेस मॉडलिंग (एसएसएम), रूसी अनुवाद में - स्टेट स्पेस मॉडल।
टिप्पणीइस क्षेत्र में कई अंग्रेजी-भाषा के नामों के लिए, अनुवाद या तो उपलब्ध नहीं है, या विभिन्न अनुवादकों के बीच भिन्न होता है, या एक सभ्य समाज में इसका उपयोग करने की पूरी असंभवता से अनाड़ी है। इसलिए, अंग्रेजी संस्करण में कई नाम दिए जाएंगे। रुचि रखने वालों के लिए, मॉडलिंग एसएसएम पर सबसे अच्छी
पुस्तकों में से एक। यह भी पता चला कि रूसी अनुवाद में इस विषय पर व्यावहारिक रूप से अच्छी किताबें नहीं हैं। एक विकल्प के रूप में - अलेक्जेंडर Tsyplakov का
काम , जो, हालांकि एक अलग लेख के रूप में प्रकाशित किया गया था, वास्तव में एक अत्यंत अपमानित संस्करण में पुस्तक की एक प्रति है।
तो चलिए शुरू करते हैं।
1. प्रारंभिक डेटा विश्लेषण
यह हिस्सा प्रक्रिया के सबसे महत्वपूर्ण हिस्सों में से एक है, क्योंकि यदि आप अभी गलती करते हैं, तो बाकी सभी काम सिर्फ समय की बर्बादी हो सकते हैं। हम मास्को क्षेत्र के एक गोदाम परिसर में माल के शिपमेंट पर
डेटा खोलते हैं, जिसका उपयोग पिछले लेख में किया गया था। चलो साजिश करते हैं:
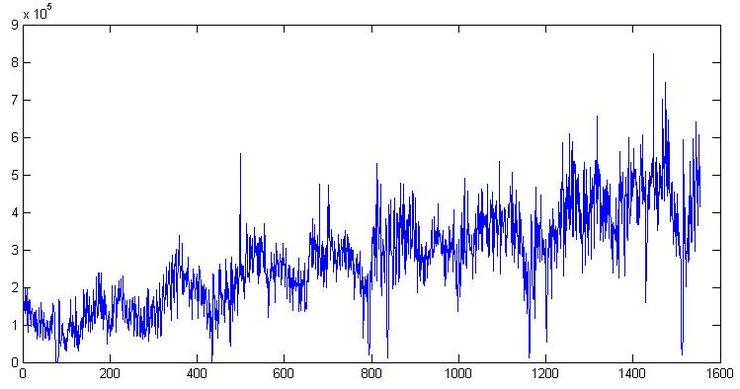
सबसे पहले, लगभग 300 दिनों के आदेश के साथ स्पष्ट रूप से एक प्रवृत्ति और एक चक्र है। अब चार्ट को बंद करें। चलिए एक धुंआ है। हम आएंगे, इसे फिर से खोलेंगे और संख्याओं को स्वयं देखेंगे। शिपमेंट की तिथि 01.09.2009 प्रारूप में इंगित की गई है, इसलिए, हम इसे एक्सेल में खोलते हैं और यदि हम डेटा को प्रारूप
[$ -F800] dddd, mmmm dd, yyyy] में स्थानांतरित करते हैं
, ताकि सप्ताह का दिन प्रदर्शित हो, तो हम ध्यान दें कि आमतौर पर शनिवार को शिपमेंट मान बहुत कम होते हैं। सप्ताह के बाकी दिनों की तुलना में। एक उदाहरण के लिए, चार्ट 1 में दो सप्ताह दिखाए गए हैं। सामान्य तौर पर, लोडर अंकल वस्या फुटबॉल देखने के लिए शनिवार की सुबह घर से बाहर निकलते हैं, और इस वजह से हमें 7-दिन के मौसम के साथ माइक्रो साइकिल की उपस्थिति को भी ध्यान में रखना होगा। वैसे, हम पिछले लेख के अनुसार साप्ताहिक अंतराल में डेटा स्थानांतरित नहीं करेंगे, लेकिन दैनिक डेटा के साथ काम करना जारी रखेंगे।
2. राज्य अंतरिक्ष मोड
यहाँ मैं कम से कम सिद्धांत देने की कोशिश करूँगा, अधिक विस्तार से कि क्यों और कहाँ से आए सभी सूत्र किताब में पढ़े जा सकते हैं या मैं टिप्पणियों में उत्तर दूंगा।
मान लीजिए कि एक निश्चित समय श्रृंखला है
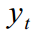
, हमारे मामले में, माल के शिपमेंट पर डेटा। जैसा कि
कुज़नेत्सोविन ने पिछले लेख में सही ढंग से बताया है, डेटा स्पष्ट रूप से 1 के एकीकरण क्रम के बगल में गैर-स्थिर है, और एआरआईएमए प्रक्रिया को श्रृंखला के भेदभाव की आवश्यकता होगी। लेकिन जब से हम हार्वे [1993] का अनुसरण नहीं करना चाहते हैं, तो हम यह मान लें कि इस श्रृंखला को एक मॉडल के रूप में निरूपित किया जा सकता है जिसमें असंगत घटक हैं

जहाँ
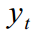
- टाइम
टी में देखी गई श्रृंखला, जिसमें अप्राप्य घटक होते हैं: प्रवृत्ति
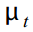
, चक्र
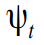
मौसमी चर
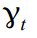
(हमारे मामले में, एक सप्ताह के बराबर), और त्रुटियां
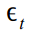
जिसे आम तौर पर सफेद शोर के रूप में वितरित किया जाता है
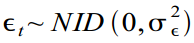
।
स्थानीय रेखीय प्रवृत्ति के मॉडल के रूप में इसका निर्माण करके एक प्रवृत्ति को विविधता दी जा सकती है:
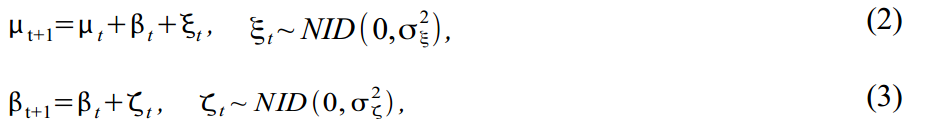
जहां (2) स्वयं की प्रवृत्ति है और (3) प्रत्येक अपनी स्वयं की त्रुटियों के साथ प्रवृत्ति ढलान है। ऐसा मॉडल ट्रेंड मॉडलिंग के लिए कई विकल्प प्रदान करता है, जिसमें ड्रिफ्ट के साथ रैंडम वॉक से लेकर इंटीग्रेटेड रैंडम वॉक मॉडल शामिल हैं। कई अर्थशास्त्री अक्सर (2) चिकनी चिकनी प्रवृत्ति प्राप्त करने के लिए त्रुटि को दूर करते हैं, और प्रवृत्ति ढलान को सभी यादृच्छिक त्रुटियों को असाइन करते हैं।
स्टोचैस्टिक चक्र को त्रिकोणमितीय कार्यों और उनके डेरिवेटिव के योग के रूप में तैयार किया गया है:
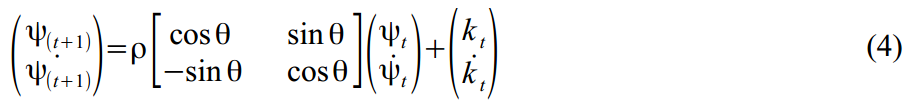
जहाँ
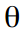
चक्र की आवृत्ति को दर्शाता है, जिसे रेडियन में मापा जाता है
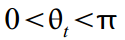
एक चक्र अवधि के साथ, क्रमशः
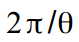
। यदि आपके पास एक मूड और अतिरिक्त समय है, तो आप मान सकते हैं कि आवृत्ति समय के साथ बदलती है:

, लेकिन हम अपनी आँखें बंद कर लेते हैं और यह मान लेते हैं कि हमारा चक्र पूरी तरह से स्थिर है। क्षीणन गुणांक यह सुनिश्चित करने के लिए जिम्मेदार है कि हमारा चक्र उचित सीमाओं से परे नहीं उड़ता है:
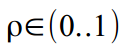
।
और अंत में, त्रिकोणमितीय कारक के योग के आधार पर एक साप्ताहिक माइक्रो साइकिल की अवधि s = 7 के साथ भी निर्माण किया जाएगा:

अब यह उपरोक्त सभी फ़ार्मुलों को कलामन फ़िल्टर के लिए उपयुक्त तथाकथित संरचनात्मक प्रारूप में व्यवस्थित करने के लिए बना हुआ है:
माप समीकरण हमारे द्वारा देखे जाने वाले डेटा का वर्णन करता है:

और संक्रमण समीकरण - चर बनाने वाले की गतिशीलता का वर्णन करता है
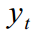
, लेकिन हम उन्हें (तथाकथित अप्रचलित या अव्यक्त चर) नहीं देखते हैं:

हमारे मामले में, 10 अव्यक्त चर हैं जो समीकरणों में परिभाषित किए गए थे (2) - (6):
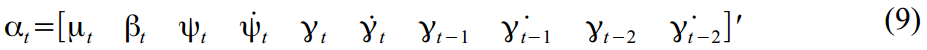
अब हम उपरोक्त सभी सूत्र मैट्रिक्स प्रारूप में अनुवाद करेंगे।
संक्रमण मैट्रिक्स (7) में:
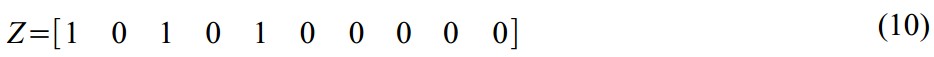
(8) में अव्यक्त चर की गतिशीलता का इतना कमजोर मैट्रिक्स:
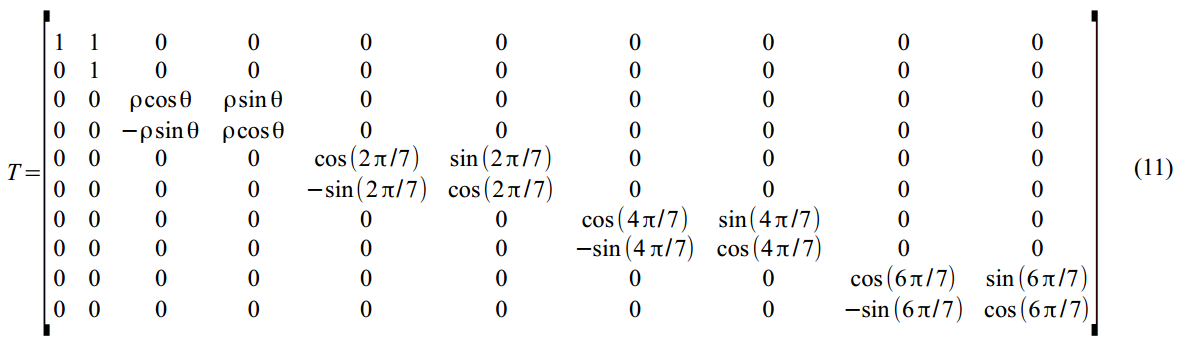
सभी राज्यों की सभी त्रुटियों का वेक्टर (2) - (6):

जो मैट्रिक्स का उपयोग करके गतिशीलता (8) के समीकरणों में एम्बेडेड है
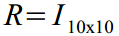
।
और अंत में, (8) में सभी त्रुटियों और गड़बड़ियों की विविधताओं का मैट्रिक्स:

3. फ़िल्टर और कलमन चिकना
ठीक है, अब हम कलमन को धूम्रपान करने के लिए तैयार हैं। हमने पहले से ही फिल्टर एल्गोरिदम के बारे में
एक से अधिक बार लिखा है , जब तक कि हमने चर पदनामों के
नाम और उपनामों को थोड़ा बदल नहीं दिया है। इसलिए, हम बहुत कम समय के लिए, लगभग चालीस मिनट के लिए सिद्धांत पर ध्यान केंद्रित नहीं करेंगे। तो एक दृश्यमान चर है
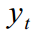
, और अदृश्य का एक सेट

, जिसके लिए हम (8) - (14) में गतिशीलता और संरचना के साथ आए थे, और जिसे हम कलमन फिल्टर का उपयोग करके
तोते में गणना करने की कोशिश करते हैं। चूंकि अव्यक्त अवस्थाएं अदृश्य हैं, इसलिए मॉडल बहुत सही नहीं हो सकता है, और विभिन्न माप त्रुटियां आवश्यक रूप से मौजूद हैं, फिर

हम मिलने की संभावना नहीं है, लेकिन अवलोकन डेटा
1, .., t-1 के आधार पर केवल समय पर इसकी गणितीय अपेक्षा:
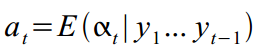
जिसका फैलाव है
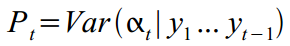
।
प्रारंभिक मान लें
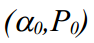
ज्ञात हैं (एल्गोरिथ्म के कार्यान्वयन के व्यावहारिक भाग में, हम बस छत से मूल्यों को निर्धारित करते हैं), कलमन फ़िल्टर में पुनरावृत्तियों का एक सेट होता है:

जहाँ
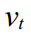
- बदलाव के साथ एक बार के पूर्वानुमान की त्रुटि

।
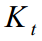
- कलमन लाभ, और इसी तरह। सामान्य तौर पर, सिद्धांत अफ्रीका में एक ही है - भौतिकी और भूगोल दोनों में। केवल लेखक के अनुरोध पर चर के पदनाम बदल जाते हैं।
राज्य वेक्टर की गणना करने के अलावा, हमारे लिए व्यक्तिगत मॉडल मापदंडों को खोजना अभी भी दिलचस्प है, जैसे कि, उदाहरण के लिए, त्रुटि भिन्नता, चक्र आवृत्ति, और चक्र क्षीणन पैरामीटर। हम वांछित मापदंडों के वेक्टर को कहते हैं
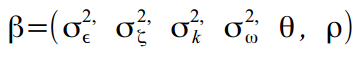
। तब अगर
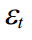
और
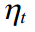
गॉस के अनुसार वितरित किया जाता है, फिर हमारे डेटा के लिए मापदंडों का लॉग-लाइबिलिटी फ़ंक्शन होगा:
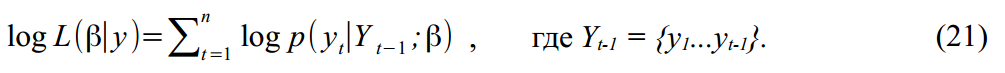
क्योंकि
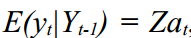
और
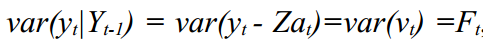
फिर कलमन फ़िल्टर के परिणाम का उपयोग फ़िल्टर त्रुटियों के आधार पर संभावना फ़ंक्शन की गणना करने के लिए किया जा सकता है:
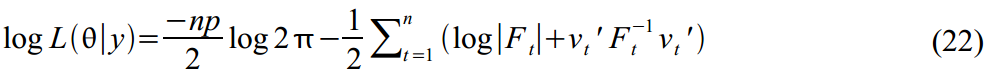
इस फ़ंक्शन को अधिकतम करके, हम आवश्यक मापदंडों के अनुमान पा सकते हैं
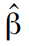
। व्यवहार में, कार्यों को कम करना हमेशा आसान होता है, इसलिए (22) में हमने माइनस संकेत जोड़े हैं, और हम इसे कम से कम करेंगे।
अब एक और wunderwaffe के बारे में कुछ शब्द - कलमन स्मूथी (Kalman smoother), [डर्बिन, जे।, और कोपमैन, 2003], जो कि हैबे पर उल्लेख नहीं किया गया है। सामान्य तौर पर, विचार समान है, केवल कलमन फ़िल्टर प्रत्येक बाद के मूल्य की गणना करता है
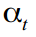
समय
टी पिछले डेटा
1..t-1 पर आधारित है:
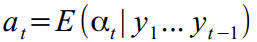
। और कलमन स्मूथर थोड़ा पढ़ता है, और, यह मानते हुए कि हमारे पास पहले से ही सभी डेटा हैं, यह स्पष्ट करना संभव बनाता है
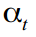
पूरे समय श्रृंखला को देखते हुए
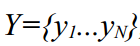
, अर्थात्, सरल शब्दों में, वह गणना करता है
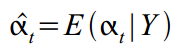
। यह तब अच्छी तरह से काम करता है जब हमारे पास पहले से ही सभी अवलोकन हैं, और यह भविष्य का अनुमान नहीं है कि हमारी रुचि है, लेकिन यह अव्यक्त चर
के सटीक मूल्यों
को तैयार करना बेहतर है जो श्रृंखला की गतिशीलता बनाते हैं।
Kalman चौरसाई रिवर्स पुनरावृत्ति है:

जहां स स स स स स स स स स स स स
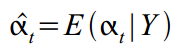
सबसे छोटा संस्करण होगा
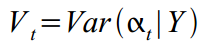
। चौरसाई पुनरावर्तन समय
टी = एन पर शुरू होता है, और वेक्टर को शून्य मान सेट करके पीछे की ओर शुरू होता है
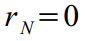
और इसका फैलाव
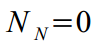
। भविष्यवाणी त्रुटि मान
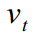
इसका विचरण

और Kalman लाभ
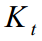
फिल्टर से लिया गया है, जो पहले रन में संचालित है।
सामान्य तौर पर, आप सिद्धांत के बारे में लंबे समय तक लिख सकते हैं, लेकिन आपके हाथ पहले से ही परीक्षण करने के लिए खुजली कर रहे हैं। तो, चलिए अनुभवजन्य भौतिकवाद की ओर बढ़ते हैं।
4. प्रतिगमन
मैं मतलबा में निम्नलिखित कार्यक्रमों की अनुकूलता और गति का ढोंग नहीं करता, मैं एक वास्तविक वेल्डर नहीं हूं, सभी कोड खुद के लिए लिखे गए थे। असामान्य, लेकिन सस्ते, विश्वसनीय और व्यावहारिक। इसके अलावा, फिल्टर और स्मूथिंग के लिए कोड कुछ हद तक बेमानी है, क्योंकि यह विभिन्न इनिशियलाइज़ेशन विकल्पों के लिए लिखा गया है, आदि। कोड के हिस्से को अनिवार्य रूप से बाहर फेंकने के प्रयास ने मैट्रिस और लूप्स में मैटलैब क्रैश कर दिया, और इसलिए मैंने सब कुछ छोड़ने का फैसला किया।
सब कुछ इस तरह काम करता है:
- मुख्य कार्यक्रम otgr_ssm.m डेटा डाउनलोड करता है, ssmopt संरचना तैयार करता है, जिसमें कई मूल्यवान नोट और महत्वपूर्ण चर लिखे जाते हैं जो कोड में विभिन्न स्थानों पर प्रेषित किए जाएंगे। शिपमेंट के लिए अंतिम 70 मान (10 सप्ताह) पूर्वानुमान के साथ तुलना के लिए अलग सेट किए जाएंगे, जिसे हम निश्चित रूप से अंत में बनाएंगे।
- डेटा को लॉग-लाइकैलिटी फ़ंक्शन अधिकतमकरण रूटीन पर अपलोड किया जाता है। बाद की प्रक्रिया अक्सर अर्थमिति में उपयोग की जाती है, इसलिए इसे जल्दी से एक सामान्य रूप में घुटने पर एक अलग फ़ंक्शन mle_my.m द्वारा लिखा गया था ताकि मुख्य कोड को कूड़े न करें।
- चूंकि मांगे गए मापदंडों में राज्यों के संस्करण शामिल हैं, इसलिए उन्हें सख्ती से सकारात्मक होना चाहिए, जो संख्यात्मक अनुकूलन के दौरान हमेशा प्राप्त नहीं होता है। इसलिए, हम प्यादों को चश्मे में बदलते हैं और सभी इनपुट विचरण मूल्यों को रूपांतरित किया जाएगा
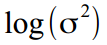 , और क्षीणन गुणांक सीमा में सामान्यीकृत होता है
, और क्षीणन गुणांक सीमा में सामान्यीकृत होता है 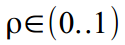 कैसे
कैसे 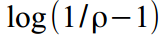 । खैर, आउटपुट पर, वे अपने उचित मूल्यों में वापस बदल जाते हैं -
। खैर, आउटपुट पर, वे अपने उचित मूल्यों में वापस बदल जाते हैं - 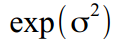 विविधताओं के लिए और
विविधताओं के लिए और  क्षीणन गुणांक के लिए। मान ssmopt.trans इंगित करता है कि (1) या नहीं (0) को रूपांतरित किया जाना चाहिए, और किस दिशा में - 'इन', या 'आउट'। यह सब एक अलग ट्रांसफॉर्मेशन फ़ंक्शन के साथ होता है
क्षीणन गुणांक के लिए। मान ssmopt.trans इंगित करता है कि (1) या नहीं (0) को रूपांतरित किया जाना चाहिए, और किस दिशा में - 'इन', या 'आउट'। यह सब एक अलग ट्रांसफॉर्मेशन फ़ंक्शन के साथ होता है - mle_my.m , ऑब्जेक्ट फ़ंक्शन को f_obj.m कहता है , जो कलमन फ़िल्टर (15) चलाता है - (22) kfmy2.m का उपयोग करके , लॉग- लाइबिलिटी फ़ंक्शन (22) के मान की गणना करता है, और, दो बार उठने के क्रम में, कलमन स्मूथिंग (23) की गणना नहीं करता है ) - (27) ksmy2.m का उपयोग करते हुए । यह सब mle_my.m पर वापस चला जाता है, जो यह जांचता है कि हम अधिकतम फ़ंक्शन (22) तक पहुंच गए हैं या नहीं। यदि हाँ, तो सभी चरण 5 पर जाते हैं। यदि नहीं, तो चरण 2-4 दोहराएं।
बहुत पहले फ़िल्टर रन इस धारणा से शुरू होता है कि 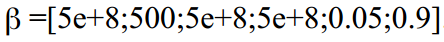 । यहां आप चारों ओर खेल सकते हैं, क्योंकि कई चर हैं, और हम एक वैश्विक अधिकतम छह-आयामी फ़ंक्शन की तलाश कर रहे हैं, इसलिए कई स्थानीय एक्स्ट्रेमा संभव हैं। एक अच्छे तरीके से, कोई लॉग फ़ंक्शन के संभावित मानों के ग्राफ़ का निर्माण कर सकता है और संभावित एक्स्ट्रेमा को देख सकता है।
। यहां आप चारों ओर खेल सकते हैं, क्योंकि कई चर हैं, और हम एक वैश्विक अधिकतम छह-आयामी फ़ंक्शन की तलाश कर रहे हैं, इसलिए कई स्थानीय एक्स्ट्रेमा संभव हैं। एक अच्छे तरीके से, कोई लॉग फ़ंक्शन के संभावित मानों के ग्राफ़ का निर्माण कर सकता है और संभावित एक्स्ट्रेमा को देख सकता है। - हम परिणाम प्रदर्शित करते हैं - पाया पैरामीटर और रेखांकन। उसी समय, हम 70 दिनों के लिए भविष्यवाणी की गणना करते हैं और frcst.m का उपयोग करके वास्तविक डेटा के साथ इसकी तुलना करते हैं
वास्तव में, कोड:
otgr_ssm.mclear all; clc; close all; format long;
mle_my.m function result_mle=mle_my(y,mleopt); warning off; %---------------- 1. Set-up minimization options ---------------- options=optimset('fminunc'); options=optimset('LargeScale', 'off' , ... 'HessUpdate', 'bfgs' , ... 'LineSearchType', 'quadcubic' , ... 'GradObj' , 'off' , ... 'Display','off' , ... 'MaxIter' , 1000 , ... 'TolX', 1e-12 , ... 'TolFun' , 1e-12, ... 'DerivativeCheck' , 'off' , ... 'Diagnostics' , 'off' , ... 'MaxFunEvals', 1000); %---------------- 2. Run minimization ---------------- [b,fval,exitflag,output,grad,hessian]=fminunc(mleopt.mle,mleopt.sv,options,y,mleopt); warning on; result_mle.b=b; result_mle.fval=fval; result_mle.output=output; result_mle.hessian=hessian;
f_obj.m function [obj,KF_out,Ksm_out]=f_obj_tr(b,y,ssmopt); %---------------- 1. Recover parameters ------------------------------------ b=transform(b,'out',ssmopt); s2_irr=b(1); s2_tr=b(2); s2_cyc=b(3); s2_seas=b(4); freq=b(5); rho=b(6); %---------------- 2. Build the model ------------------------------------ ssmopt.ssmodel.states=10; ssmopt.ssmodel.Z=[1 0 1 0 1 0 1 0 1 0]; T1 = [1 1 0 0; 0 1 0 0; 0 0 rho*cos(freq) rho*sin(freq); 0 0 -rho*sin(freq) rho*cos(freq)]; T2=[cos(2*pi/7) sin(2*pi/7) 0 0 0 0;... -sin(2*pi/7) cos(2*pi/7) 0 0 0 0;... 0 0 cos(4*pi/7) sin(4*pi/7) 0 0;... 0 0 -sin(4*pi/7) cos(4*pi/7) 0 0;... 0 0 0 0 cos(6*pi/7) sin(6*pi/7);... 0 0 0 0 -sin(6*pi/7) cos(6*pi/7)]; ssmopt.ssmodel.T = [T1 zeros(rows(T1),cols(T2));zeros(rows(T2),cols(T1)) T2]; ssmopt.ssmodel.R=eye(10); ssmopt.ssmodel.R(1,1)=0; H=s2_irr; Q=zeros(10,10); Q(2,2)=s2_tr; Q(3,3)=s2_cyc; Q(4,4)=s2_cyc; Q(5,5)=s2_seas; Q(6,6)=s2_seas; Q(7,7)=s2_seas; Q(8,8)=s2_seas; Q(9,9)=s2_seas; Q(10,10)=s2_seas; %---------------- 3. Suggest starting conditions for the states ------------------------ a0=[y(1);0;0;0;0;0;0;0;0;0]; P0=eye(ssmopt.ssmodel.states)*1e+10; %---------------- 4. Run Kalman filter ------------------------ KF_out = feval(ssmopt.filter,y, ssmopt, Q, H, a0, P0); obj=KF_out.LH; %---------------- 5. Run Kalman smoother ------------------------ if nargout>2 ssmopt.ssmodel.num_etas=3; % number of the state variances (required for Kalman smoother) Ksm_out = feval(ssmopt.smooth,KF_out, ssmopt); end
ksmy2.m function [Ksm_out, Kdism_out] = ksmy2(KF_out, ssmopt); [m,N]=size(KF_out.Afilt); meta=ssmopt.ssmodel.num_etas; %---------------- 1. Recover filtered matrices ---------------- Fmat=KF_out.Fmat; Vmat=KF_out.Vmat; Pfilt=KF_out.Pfilt; Afilt=KF_out.Afilt; Q=KF_out.Q; H=KF_out.H; %---------------- 2. Recover Model structure ---------------- Z=ssmopt.ssmodel.Z; T=ssmopt.ssmodel.T; R=ssmopt.ssmodel.R; Asm=zeros(m,N); Psm=zeros(m,m,N); rmat=zeros(m,N); Nmat=zeros(m,m,N); Eps=zeros(1,N); Eta=zeros(meta,N); Kmat=KF_out.Kmat; Lmat=KF_out.Lmat; if ~isfield(KF_out,'exact'); KF_out.exact.d=0; end d=KF_out.exact.d; if KF_out.exact.d>0 L1=KF_out.exact.L1; F1=KF_out.exact.F1; F2=KF_out.exact.F2; Pinf=KF_out.exact.Pinf; end %---------------- 3. Regular Smoothing for t=N..d+1 observations ---------------- for i=N:-1:d+1 r=Z'/Fmat(i)*Vmat(i) + Lmat(:,:,i)'*rmat(:,i); N=Z'/Fmat(i)*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r; Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i); if i>1 rmat(:,i-1)=r; Nmat(:,:,i-1)=N; end if nargout>1 Eps(i)=H*(1/(Fmat(i))*Vmat(i)-Kmat(:,i)'*rmat(:,i)); Eta(:,i)=Q*R'*rmat(:,i); end end %---------------- 4. Exact Smoothing for t=d..1 observations ---------------- if KF_out.exact.d>0 r1=zeros(m,1); N1=zeros(m,m); N2=zeros(m,m); for i=d:-1:1 if sum(Pinf(:,:,i)*Z')>0 %cond(Pinf)<1e+12 % Pinf is not singular r1=Z'*F1(i)*Vmat(i) + Lmat(:,:,i)'*r1 + L1(:,:,i)'*rmat(:,i); N2=Z'*F2(i)*Z + Lmat(:,:,i)'*N2*Lmat(:,:,i) + Lmat(:,:,i)'*N1*L1(:,:,i) + L1(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*L1(:,:,i); N1=Z'*F1(i)*Z + Lmat(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); r=Lmat(:,:,i)'*r1; N=Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); if nargout>1 Eps(i)=-H*Kmat(:,i)'*rmat(:,i); Eta(:,i)=Q*R'*rmat(:,i); end else % Pinf is singular r1=T'*rmat(:,i); N2=T'*N2*T; N1=T'*N1*Lmat(:,:,i); r=Z'/(Fmat(i))*Vmat(i) + Lmat(:,:,i)'*rmat(:,i); N=Z'/(Fmat(i))*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); if nargout>1 Eps(i)=H*(1/Fmat(i)*Vmat(i) - Kmat(:,i)'*rmat(:,i)); Eta(:,i)=Q*R'*rmat(:,i); end end if i>1 rmat(:,i-1)=r; Nmat(:,:,i-1)=N; end Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r + Pinf(:,:,i)*r1; Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i) - (Pinf(:,:,i)*N1*Pfilt(:,:,i))' - Pinf(:,:,i)*N1*Pfilt(:,:,i) - Pinf(:,:,i)*N2*Pinf(:,:,i); end end %---------------- 5. Prepare output ---------------- Ksm_out.Asm=Asm; Ksm_out.Psm=Psm; Ksm_out.Kmat=Kmat; Ksm_out.Lmat=Lmat; Ksm_out.Nmat=Nmat; Ksm_out.rmat=rmat; Kdism_out.Eps=Eps; Kdism_out.Eta=Eta;
transform.m function b=transform(b,howto,ssmopt); k=length(b); if strcmp(howto,'in') % in-transformation if ssmopt.trans==0 % no transformation b=b; end; if ssmopt.trans==1 % transformation to preserve the positiveness of variances b(1:k-1,:)=log(b(1:k-1,:)); b(k)=log(1/b(k)-1); end; else % out-transformation if ssmopt.trans==0 % no transformation b=b; end; if ssmopt.trans==1 b(1:k-1,:)=exp(b(1:k-1,:)); b(k)=1/(1+exp(b(k))); end; end
5. परिणाम
(पाया रेटिंग्स के पी-मान कोष्ठकों में दर्शाए गए हैं)
प्रेक्षित श्रृंखला की त्रुटि का विचरण 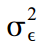 | 1.77 ई + 009 (0.00) |
ट्रेंड त्रुटि विचरण 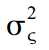 | 348.73 (0.00) |
चक्र फैलाव 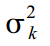 | 6.07E + 008 (0.00) |
मौसमी घटक त्रुटि की भिन्नता 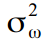 | 3.91 ई + 006 (0.00) |
चक्र की आवृत्ति 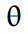 | 3.91 ई + 006 (0.00) |
| चक्र अवधि (दिनों में) | 362.6 (0.00) |
पाश क्षीणन गुणांक 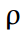 | 0.891 (0.00) |
| R- चुकता प्रतिगमन | 0.78 |
6. चार्ट
धारणा में आसानी के लिए, ग्राफ केवल पहले 600 दिनों के लिए दिखाए जाते हैं, पूरी श्रृंखला के लिए वे स्पॉइलर के नीचे छिपे हुए हैं।
एक। कच्चा, फ़िल्टर्ड और चिकना डेटा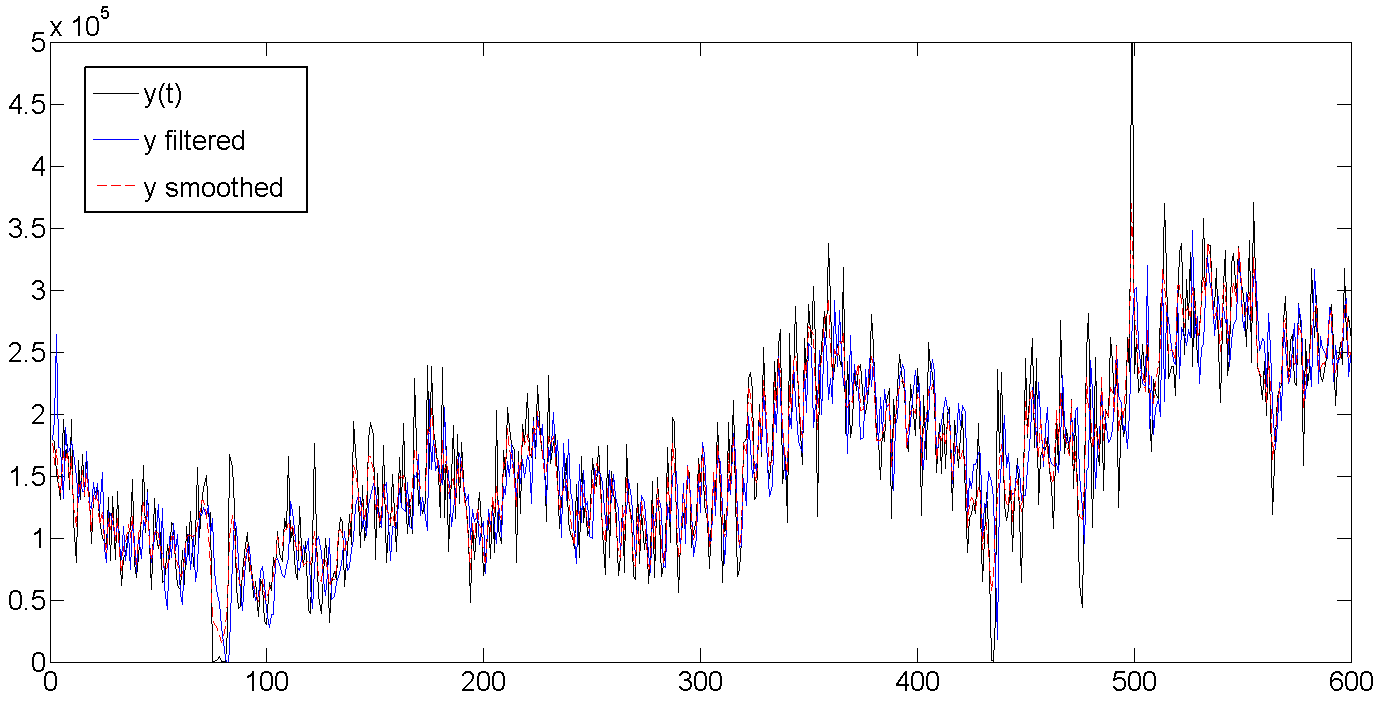 ख। स्रोत डेटा, फ़िल्टर्ड प्रवृत्ति, स्मूद ट्रेंड
ख। स्रोत डेटा, फ़िल्टर्ड प्रवृत्ति, स्मूद ट्रेंडजैसा कि आप देख सकते हैं, कलमन फ़िल्टर पिछले मानों के आधार पर प्रवृत्ति का अनुमान लगाने की कोशिश कर रहा है, और इसलिए पार्टी की रेखा के साथ-साथ उतार-चढ़ाव होता है, लेकिन थोड़ा देर हो चुकी है, यह अनुमान लगाने की कोशिश कर रहा है कि हमारा डेटा आगे कहां जाएगा। कलमैन चिकनी पूरी श्रृंखला को "देखता है", और इसलिए प्रवृत्ति बहुत चिकनी और शांत दिखती है:
 सी। फ़िल्टर्ड एंड स्मूथ्ड लूप
सी। फ़िल्टर्ड एंड स्मूथ्ड लूपजैसा कि परिणाम के साथ तालिका से देखा जा सकता है, औसत चक्र की लंबाई लगभग 362 दिन है, या लगभग एक वर्ष (जो आश्चर्यचकित होगा)। आप यह भी देख सकते हैं कि फ़िल्टर को शुरू करने और डेटा को पूरी तरह से याद करने की शुरुआत में कैसे शुरू होता है, क्योंकि हम अव्यक्त चर के प्रारंभिक मानों को शून्य पर सेट करते हैं और 1e + 10 के क्रम का एक बहुत बड़ा फैलाव। लेकिन आम तौर पर कुछ (2-5) पहले प्रयास ताल को फिल्टर में लाने के लिए पर्याप्त होते हैं। वैसे, इस काम में हमने फ़िल्टर के सटीक इनिशियलाइज़ेशन (सटीक इनिशियलाइज़ेशन) का उपयोग किया, जो फ़िल्टर्ड मानों को डेटा पर जल्दी से प्राप्त करने में मदद करता है।
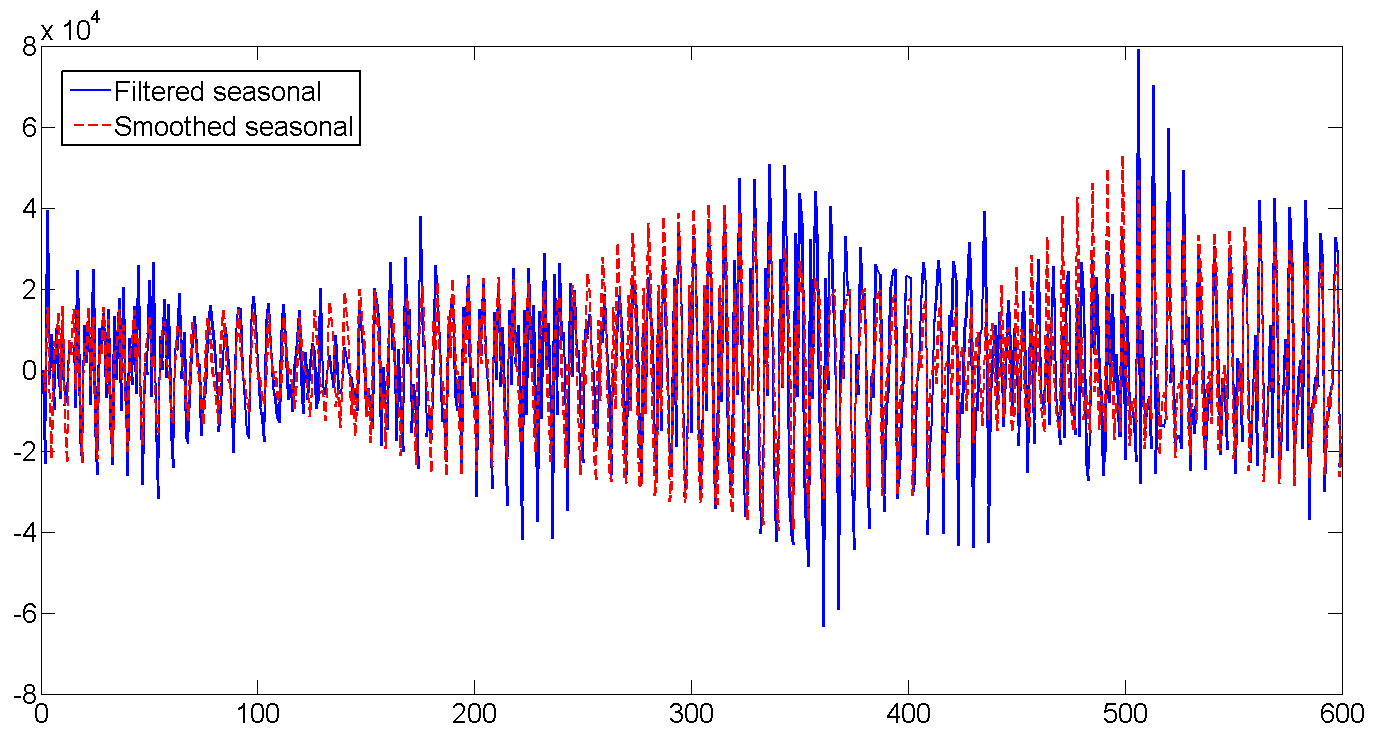
 घ। फ़िल्टर्ड और स्मूथेड साप्ताहिक मौसमी कारक
घ। फ़िल्टर्ड और स्मूथेड साप्ताहिक मौसमी कारकशिपमेंट की संख्या धीरे-धीरे बढ़ रही है, और दैनिक अस्थिरता बढ़ रही है:
6. पूर्वानुमान
प्राप्त मापदंडों के आधार पर और फ़िल्टर्ड राज्यों के नवीनतम मूल्यों का उपयोग करके, हम 70 दिनों (10 सप्ताह) के लिए पूर्वानुमान का निर्माण करते हैं और मौजूदा डेटा से इसकी तुलना करते हैं। सामान्य तौर पर, पूर्वानुमान अच्छा लगता है, यही जीवन देने वाला फ़िल्टर करता है। सप्ताह के दिन तक निर्देशित अस्थिरता विशेष रूप से मनभावन होती है। यदि आप निर्मित पूर्वानुमान की पूरी लंबाई को बारीकी से देखते हैं और कल्पना को चालू करते हैं, तो आप यह भी देख सकते हैं कि पूर्वानुमान वार्षिक शिपमेंट चक्र के तहत कैसे झुकता है। एकमात्र क्षण जहां पूर्वानुमान काम नहीं करता था वह 26 से 32 दिनों का होता है। लेकिन स्पष्ट रूप से शिपिंग में लगभग साप्ताहिक गिरावट आई, साथ ही साथ इसके तुरंत बाद एक तेज छलांग भी लगी, जो कि शायद ही कभी संभव हो पाए, क्योंकि इस तरह का मामला केवल श्रृंखला की शुरुआत में एक बार हुआ था। सामान्य तौर पर, और जो गिर गया वह बादल से है।
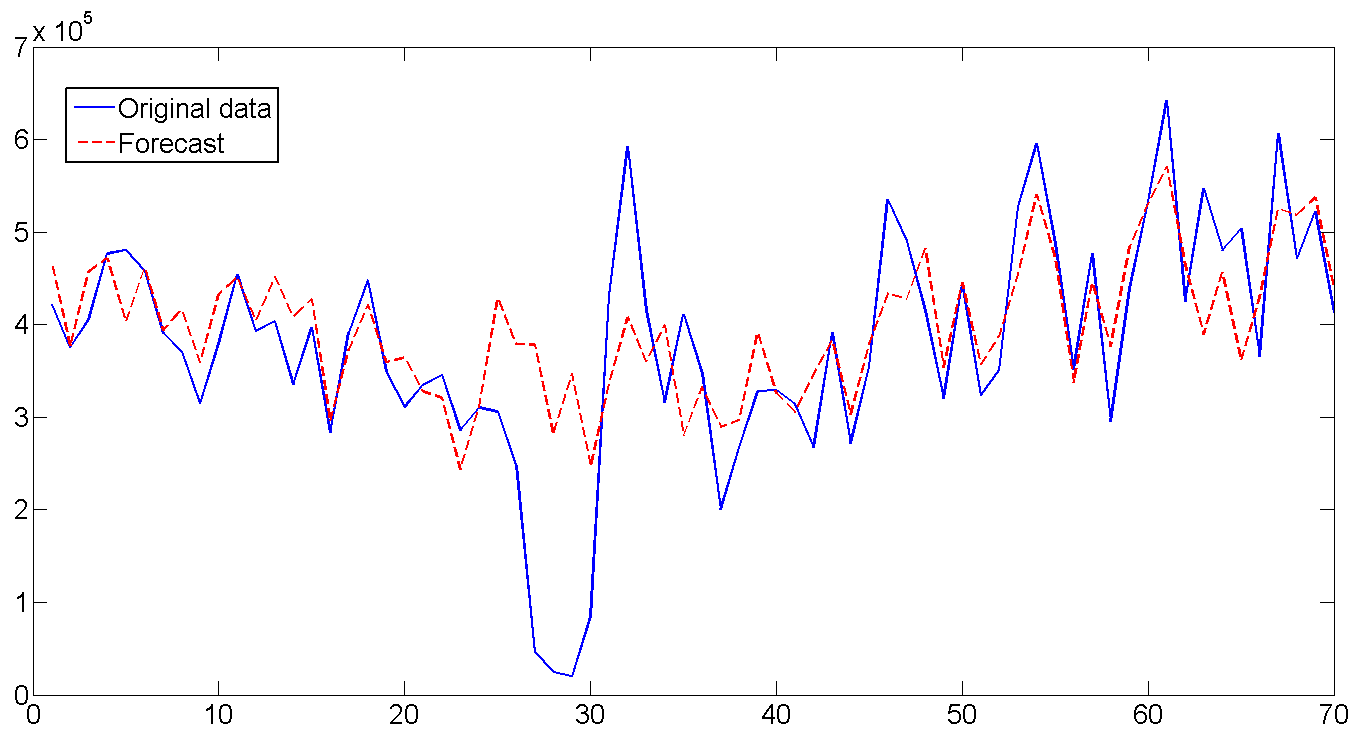
यदि हम मॉडल की तुलना करना चाहते हैं, तो RMSE का पूर्वानुमान 1.112e + 005 है।
खैर, यह सब है।
टिप्पणीस्टेट स्पेस मॉडल्स को इकोनॉमिक्स में कुछ सार्थक नहीं लिया जाना चाहिए। इसके विपरीत, वे कई और विशिष्ट मॉडलों के लिए एक सामान्यीकृत संस्करण का प्रतिनिधित्व करते हैं। उदाहरण के लिए, एमए (1) प्रक्रिया

SSM फॉर्म में कल्पना करना आसान:
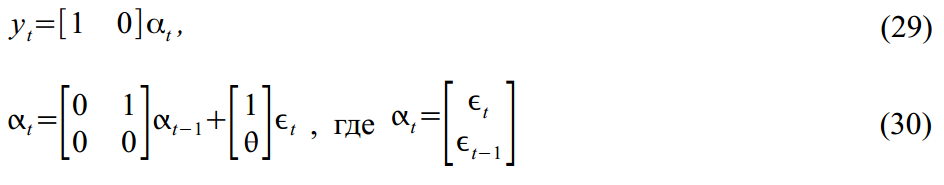
या ARMA (2,1) प्रक्रिया:
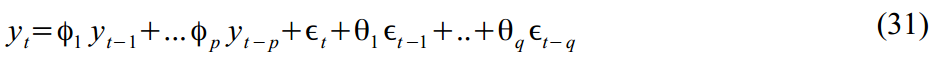
SSM प्रारूप में पैक किया गया:
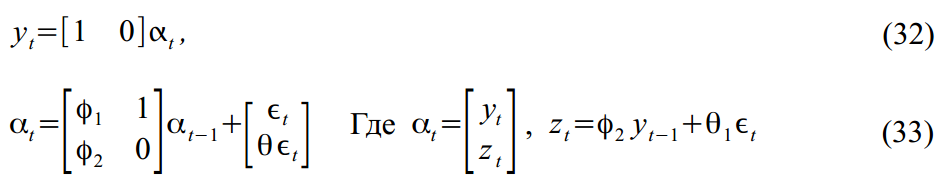
संबंधित साहित्य- डर्बिन, जे।, और कोपमैन, राज्य अंतरिक्ष विधियों द्वारा एसजे टाइम सीरीज विश्लेषण। ऑक्सफोर्ड: ऑक्सफोर्ड यूनिवर्सिटी प्रेस, 2001।
- डर्बिन, जे।, और कोपमैन, एसजे "राज्य अंतरिक्ष समय श्रृंखला विश्लेषण के लिए एक सरल और कुशल सिमुलेशन चिकनी" बायोमेट्रिक वॉल्यूम। 89, अंक 3, 2002।
- हार्वे, एसी, और जेगर, ए। "विवरण, शैलीगत तथ्य और व्यापार चक्र।" जर्नल ऑफ़ एप्लाइड इकोनोमेट्रिक्स (8), 1993।
- हार्वे, एसी "फोरकास्टिंग, स्ट्रक्चरल टाइम सीरीज़ मॉडल और कलमैन फ़िल्टर।" कैम्ब्रिज: कैम्ब्रिज यूनिवर्सिटी प्रेस, 1989।