एक पॉइसन प्रक्रिया की मॉडलिंग करना

परिचय

प्रकृति में देखी गई सबसे महत्वपूर्ण प्रक्रियाओं में से एक पॉइज़न बिंदु प्रक्रिया है। इसलिए, यह समझना महत्वपूर्ण है कि ऐसी प्रक्रियाओं को कैसे मॉडल किया जा सकता है। पोइसन बिंदु प्रक्रिया के प्रकार के आधार पर मॉडलिंग के तरीके भिन्न होते हैं, अर्थात्, वह स्थान जिसमें प्रक्रिया होती है और प्रक्रिया की समरूपता या विषमता होती है। हम एक पॉइसन बिंदु प्रवाह के विकास या विभिन्न क्षेत्रों में इसके महत्वपूर्ण अनुप्रयोगों के साथ रुचि नहीं लेंगे। इस सामग्री को दिलचस्प बनाने के लिए, पाठक से आग्रह किया जाता है कि वह मूल सिद्धांत और आईटी में अनुप्रयोगों के लिए त्रिवेदी (1982) के कुछ खंडों के लिए फेलर (1965) और सिनलर (1975) में संबंधित अनुभागों को पढ़ें।

पहले चरण में, हम Poisson प्रक्रिया को [0; +।) पर परिभाषित करते हैं। प्रक्रिया पूरी तरह से यादृच्छिक घटनाओं के परिवार द्वारा निर्धारित होती है जो कुछ यादृच्छिक समय पर होती है 0 <T1 <T2 <... ये घटनाएं कई चीजों से संबंधित हो सकती हैं, जैसे कि बैंक डकैती, पांच जुड़वा बच्चों का जन्म, और एक मोंटाना टैक्सी से जुड़ी दुर्घटना। यदि N (t1, t2) समय अंतराल (t1, t2) के दौरान हुई घटनाओं की संख्या है, तो निम्नलिखित दो स्थितियां अक्सर पूरी होती हैं:

• असंबद्ध अंतराल (t1, t2) और (t3, t4) के लिए, यादृच्छिक चर N (t1, t2) और N (t3, t4) स्वतंत्र हैं
• N (t1, t2) को N के रूप में भी वितरित किया जाता है (0, t2-t1), अर्थात, एक निश्चित समय में घटनाओं की संख्या का वितरण केवल इस अंतराल की लंबाई पर निर्भर करता है।

आश्चर्यजनक तथ्य यह है कि इन दो स्थितियों में प्रवेश होता है कि सभी यादृच्छिक चर N (t1, t2) पोइसन कानून के अनुसार वितरित किए जाते हैं और यह कि एक गैर-नकारात्मक स्थिरांक λ मौजूद है जैसे कि N (t, t + a) कानून के अनुसार वितरित किया जाता है Po (λa) ) किसी भी गैर-नकारात्मक टी और ए के लिए 0। उदाहरण के लिए देखें, फेलर (1965)। इस प्रकार, पॉइसन वितरण काफी स्वाभाविक रूप से होता है।

पिछली अवधारणा को R ^d से सामान्यीकृत किया जा सकता है। A, R ^d का सबसेट है, और N एक यादृच्छिक चर है जो केवल पूर्णांक मान लेता है। X ₁ , ... X _N , A में एक मान लेने वाले यादृच्छिक वैक्टर का एक सेट है। तो हम कहते हैं कि X _i एक A पर एक समान या सजातीय Poisson प्रक्रिया को परिभाषित करता है।

• किसी भी परिमित समुच्चय के समुच्चय के समुच्चय के लिए सममित मात्रा के A A _की परिमित मात्रा, N (A ₁ ), ..., N (A _k) स्वतंत्र हैं।
• ए के किसी भी बोरेल सबसेट बी के लिए, एन (बी) का वितरण केवल बी की मात्रा पर निर्भर करता है

अनुवादक का ध्यान दें: "उपाय" शब्द का उपयोग करना बेहतर होगा, लेकिन जो लोग गणित में रुचि नहीं रखते हैं, उनके लिए एक दर्जन पृष्ठों, या इससे भी अधिक की व्याख्या करनी होगी।

फिर, इन धारणाओं में कहा गया है कि सभी N (B) को कुछ गैर-नकारात्मक λ के लिए कानून P (λVol (B)) के अनुसार वितरित किया जाता है, जिसे हम A, इस तरह के प्रक्रियाओं के तीव्रता, या एक सजातीय Poisson प्रक्रिया के तीव्रता पैरामीटर को बहुआयामी यूक्लिडियन अंतरिक्ष में कहते हैं। पेट्री डिश पर बैक्टीरिया और ह्यूस्टन हत्या शामिल हैं।

मॉडलिंग सजातीय Poisson प्रक्रियाओं

अगर हमें R A से संबंधित सेट A पर एक समान Poisson प्रक्रिया को मॉडल करने की आवश्यकता है, तो हमें A से प्रमेय 1.1 से कई यादृच्छिक वैक्टर X उत्पन्न करने की आवश्यकता है, इसे निम्नानुसार किया जा सकता है:

N λVol(A)
X1,..,XN,
RETURN 1,...,N

एन के मूल्य को उत्पन्न करने के लिए, ओ (1) की औसत जटिलता के साथ एक एल्गोरिथ्म का उपयोग करना बेकार है, चूंकि एल्गोरिथ्म के अंत में, हम कम से कम Ω (एन) संचालन खर्च करेंगे। इसलिए, यदि इस एल्गोरिथ्म का उपयोग किया जाता है, तो यह बहुत सरल एल्गोरिथ्म (ओ (λ) के रूप में बढ़ते औसत समय के साथ) के साथ एक पॉइसन यादृच्छिक चर उत्पन्न करने के लिए अत्यधिक अनुशंसित है। कुछ सेट ए के लिए, अन्य तरीकों का उपयोग किया जा सकता है जिन्हें पॉइसन यादृच्छिक चर की स्पष्ट पीढ़ी की आवश्यकता नहीं होती है। इसके उदाहरण देने के लिए हम तीन मामलों का उपयोग करते हैं।

1. ए = [0; + +)
2. ए - सर्कल
3. A - आयत

ऐसा करने के लिए, हमें पॉइसन प्रक्रिया और घातीय वितरण के बीच एक दिलचस्प संबंध की आवश्यकता है।


प्रमेय 1.2 ए = [0; + ∞;

T = 0 ( "")
k = 0 ( )
REPEAT

k = k + 1
T = T + E/λ
T[k] = T
UNTIL ( ; )

इस एल्गोरिथ्म को लागू करना आसान है क्योंकि पॉइसन यादृच्छिक चर उत्पन्न करने की कोई आवश्यकता नहीं है। अन्य सरल सेट ए के लिए, प्रमेय 1.2 के तुच्छ सामान्यीकरण हैं। उदाहरण के लिए, जब A = [0, t] x [0,1], जहां t अनंतता को बराबर कर सकता है, 0 <T1 <T2 <... तीव्रता λ और U1, U2 के साथ एक समान पॉइसन प्रक्रिया है, ... समान रूप से समान रूप से वितरित समान रूप से वितरित स्वतंत्र अनुक्रम का एक क्रम है। [0,1] यादृच्छिक चर, तब (T1, U1), (T2, U2), ... A पर तीव्रता λ के साथ पॉइसन प्रक्रिया निर्धारित करते हैं।

उदाहरण १.१।

एक यूनिट सर्कल पर यूनिफॉर्म पॉइसन प्रक्रिया
यदि A एक इकाई त्रिज्या के साथ एक चक्र है, तो एक समान Poisson प्रक्रिया के विभिन्न गुणों का उपयोग कई पीढ़ी विधियों (जो डी-आयामी क्षेत्रों के लिए सामान्यीकरण) प्राप्त करने के लिए किया जा सकता है। Λ को वांछित तीव्रता होने दें।
सबसे पहले, हम बस पैरामीटर λ and के साथ एक यादृच्छिक पॉइसन मान एन उत्पन्न कर सकते हैं, और फिर एन स्वतंत्र वैक्टर के एक क्रम को समान रूप से यूनिट सर्कल पर समान रूप से वितरित करते हैं। अगर हम प्रमेय 1.2 द्वारा प्रस्तावित क्रमिक आँकड़ों की विधि को लागू करते हैं, तो पोइसन यादृच्छिक चर अनुमानित रूप से प्राप्त किया जाता है। उदाहरण के लिए, ध्रुवीय निर्देशांक (R,,) पर जा रहे हैं, हम ध्यान दें कि एक समान Poisson प्रक्रिया के लिए, R और and स्वतंत्र हैं, और यादृच्छिक चर R का घनत्व 2r है, r 0 से 1 तक भिन्न होता है, और φ समान रूप से [0; 2π] पर वितरित किया जाता है। इस प्रकार, हम निम्नानुसार आगे बढ़ सकते हैं: एक समान Poisson प्रक्रिया उत्पन्न करें <<φ1 <...2 <... <intensityN तीव्रता पैरामीटर λ / (2π) के साथ [0; 2π] घातीय विधि और वापसी (φ1, R1), ... द्वारा; (independentN, RN), जहां Ri स्वतंत्र रूप से [0; 1] पर 2r के घनत्व के साथ यादृच्छिक चर वितरित किए जाते हैं, जिसे [0; 1] पर समान रूप से वितरित दो स्वतंत्र यादृच्छिक चर लेने से उत्पन्न किया जा सकता है। कोनों के लिए घातांक विधि को लागू करने का कोई विशेष कारण नहीं है। उसी तरह, हम रेडी उठा सकते थे। दुर्भाग्य से, क्रमिक रेडी [0; 1] पर एक आयामी यूनिफॉर्म पॉइसन प्रक्रिया नहीं बनाते हैं। हालांकि, फिर भी, वे एक अमानवीय पॉइसन प्रक्रिया बनाते हैं, और इस तरह की प्रक्रियाओं की पीढ़ी को अगले खंड में माना जाएगा।

अमानवीय Poisson प्रक्रियाओं

ऐसी परिस्थितियाँ होती हैं जब घटनाएं "यादृच्छिक समय" पर होती हैं, लेकिन कुछ क्षण दूसरों की तुलना में अधिक संभव होते हैं। यह गहन देखभाल केंद्रों पर आगमन, कंप्यूटर केंद्रों पर नौकरी की पेशकश और एनएचएल खिलाड़ियों को चोट पहुंचाने का मामला है। इन मामलों के लिए, एक बहुत अच्छा मॉडल विषम Poisson प्रक्रिया का मॉडल है, जिसे [0; + 0) पर सुविधा के लिए यहां परिभाषित किया गया है। यह सबसे महत्वपूर्ण मामला है, क्योंकि समय सबसे अधिक बार "चलने वाला चर" होता है।
[0; + is) पर अमानवीय पॉसन प्रक्रिया गैर-नकारात्मक निश्चित तीव्रता फ़ंक्शन) (t) द्वारा निर्धारित की जाती है, जिसे इस अंतर के साथ कुछ प्रकार के घनत्व के रूप में माना जा सकता है कि इसका अभिन्न [0; +! +) 1 के बराबर नहीं है (आमतौर पर, यह विचलन करता है) )। यह प्रक्रिया निम्नलिखित संपत्ति द्वारा निर्धारित की जाती है: किसी भी सीमित अंतराल के A1, A2, ..., Ak, इन अंतरालों में होने वाली घटनाओं की संख्या (N1, ..., Nk) के लिए मापदंडों पर स्वतंत्र पॉइसन यादृच्छिक चर हैं।

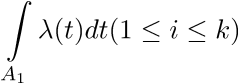
अब हम विचार करेंगे कि ऐसी प्रक्रियाओं को कैसे मॉडल किया जा सकता है। मॉडलिंग में, हम समझते हैं कि जिस समय घटनाएं होती हैं, 0 <T1 <T2 <... आरोही क्रम में दी जानी चाहिए। लुईस और शेडलर (1979) द्वारा विषम जहरीली प्रक्रियाओं के मॉडलिंग पर बहुत काम किया गया था। यह पूरा खंड उनके काम का एक संशोधित संस्करण है। यह देखना दिलचस्प है कि निरंतर यादृच्छिक चर उत्पन्न करने के सामान्य सिद्धांतों का विस्तार किया जा सकता है: हम देखेंगे कि उलटा, विचलन और रचना की विधि द्वारा एनालॉग हैं।
वितरण समारोह की भूमिका एकीकृत तीव्रता समारोह द्वारा ली जाएगी

हम यह देखते हुए शुरू करते हैं कि यदि T _n = T है, तो T _{n + 1} -T _n का वितरण फ़ंक्शन है

यदि फ़ंक्शन t (t) बढ़ती टी के साथ असीमित रूप से बढ़ता है। यह इस तथ्य से है कि



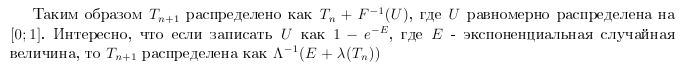
दूसरे शब्दों में, हमें Λ पलटना होगा। औपचारिक रूप से, हमारे पास सिनलर (1975) या ब्रेटली, फॉक्स और श्रेज (1983)) एक एल्गोरिथ्म है जो इंटेंसिटी फ़ंक्शन (इंटीग्रेशन मेथड) के अभिन्न के व्युत्क्रम पर आधारित है।

T = 0 ( )
k = 0 ()
REPEAT
E
k = k+1
T = T + InvΛ(E+Λ(T)), (InvΛ - Λ)
T[k] = T
UNTIL False

उदाहरण 1.2 सजातीय Poisson प्रक्रिया

विशेष मामले के लिए λ (t) = λ, t (t) = λt, यह देखना आसान है कि InvΛ (E + Λ (T)) = T + E / λ, जिसके परिणामस्वरूप हम फिर से घातीय विधि प्राप्त करते हैं।

उदाहरण १.३

जल्दी घंटे से पहले कारों के सुबह के प्रवाह का अनुकरण करने के लिए, हम कभी-कभी λ (t) = t ले सकते हैं, फिर Λ (t) = t ^ 2/2 और चरण प्राप्त कर सकते हैं

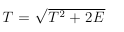
यदि तीव्रता फ़ंक्शन को तीव्रता कार्यों के योग के रूप में दर्शाया जा सकता है, अर्थात। ।

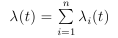
0 <T _i1 <T _i2 <... T व्यक्तिगत अमानवीय पॉसन प्रक्रियाओं का स्वतंत्र कार्यान्वयन हैं, फिर संयुक्त क्रम अनुक्रम तीव्रता फ़ंक्शन λ (t) के साथ एक अमानवीय पॉइसन प्रक्रिया के कार्यान्वयन का निर्माण करता है। यह रचना पद्धति पर लागू होता है, लेकिन अब अंतर यह है कि हमें सभी प्रक्रिया घटकों के कार्यान्वयन की आवश्यकता है। अपघटन का उपयोग तब किया जा सकता है जब विश्लेषणात्मक रूप λ (t) द्वारा निर्धारित प्राकृतिक अपघटन हो। चूंकि प्रक्रियाओं के विलय में मुख्य संचालन एन प्रक्रियाओं से न्यूनतम मूल्य लेना है, इसलिए बड़े एन के लिए एन तत्वों के ढेर में समय इंस्टेंट को संग्रहीत करके लाभ प्रदान किया जा सकता है।

परिणामस्वरूप, हम संरचना विधि प्राप्त करते हैं:

T[1,1],...,T[n,1] n
T = 0 ( )
k = 0
REPEAT
T[i,j]
k = k + 1
T[k] = T[i,j]
T[i,j+1]
UNTIL False

तीसरा सामान्य सिद्धांत थिनिंग (लुईस और शेडलर, 1979) का सिद्धांत है। विचलन विधि में ऐसा ही होता है, हम मानते हैं कि किसी भी t के लिए एक मामूली प्रभावी तीव्रता λ (t) <= μ (t) है।

फिर विचार 0 और μ (t) के बीच सकारात्मक अर्ध-समतल के भाग पर एक सजातीय पॉइसन प्रक्रिया उत्पन्न करने के लिए है, फिर λ के तहत एक सजातीय पॉइसन प्रक्रिया पर विचार करें और, आखिरकार, इस प्रक्रिया में घटनाओं के एक्स-घटकों को वापस करें। इसके लिए निम्न प्रमेय की आवश्यकता है।




अब लुईस और शेडलर को पतला करने की विधि पर विचार करें:

T = 0
k = 0
REPEAT
Z, μ, T. T = Z
[0;1] U
IF U <= λ(Z)/μ(Z)
THEN k = k + 1, X[k] = T
UNTIL False

यह तर्क दिया जाता है कि अनुक्रम x _{k ने} उत्पन्न किया एक गहन कार्य λ के साथ एक अमानवीय पॉइसन प्रक्रिया है। ध्यान दें कि हमने गैर-समरूप प्रक्रिया 0 <Y1 <Y2 <... को तीव्रता फ़ंक्शन μ के साथ लिया और कुछ बिंदुओं को हटा दिया। जहाँ तक हम जानते हैं, (Y _i , U _i μ (Y _i ) वक्र पर इकाई तीव्रता के साथ एक सजातीय Poisson प्रक्रिया है, यदि U _i स्वतंत्र यादृच्छिक चर समान रूप से [0; 1] पर समान रूप से प्रमेय के आधार पर वितरित किया जाता है। इस प्रकार, 1.3 पर। वक्र λ इस वक्र पर इकाई तीव्रता के साथ एक सजातीय Poisson प्रक्रिया को परिभाषित करता है (प्रमेय 1.3 का भाग 3.)। अंत में, केवल इस बाद के x- निर्देशांक लेने से हमें तीव्रता समारोह λ के लिए एक अमानवीय पॉइसन प्रक्रिया मिलती है।
एक गहनता समारोह μ के साथ एक अमानवीय पॉइसन प्रक्रिया आमतौर पर उलटा विधि द्वारा तैयार की जाती है।

उदाहरण १.४ चक्रीय तीव्रता समारोह

निम्नलिखित उदाहरण लुईस और शेडलर (1979) का है। प्रमुख कार्य μ = 2λ की स्पष्ट पसंद के साथ चक्रीय तीव्रता λ (t) = λ (1 + cos (t)) के साथ एक फ़ंक्शन पर विचार करें।

फिर सिमुलेशन एल्गोरिथ्म फार्म ले जाएगा:

T = 0
k = 0
REPEAT
E c 1
T = T + E/(2λ)
[0;1] U
IF U <= (1+cos(T))/2
THEN k = k + 1, X[k] = T
UNTIL False

कहने की आवश्यकता नहीं है कि ज्यादातर मामलों में कोसाइन की गणना से बचने के लिए दो पुलिसकर्मियों पर प्रमेय का उपयोग यहां किया जा सकता है।

एल्गोरिथ्म की प्रभावशीलता पर अंतिम शब्द जब एक अमानवीय पॉइसन प्रक्रिया सेट पर रखी जाती है [0, t]। घटनाओं की औसत संख्या जो प्रमुख प्रक्रिया से आवश्यक है जबकि लौटे यादृच्छिक चर की औसत संख्या है
औसत मानों के अनुपात को दक्षता के एक उद्देश्य माप के रूप में माना जा सकता है, जो मानक विचलन विधि में विचलन स्थिर की भावना में तुलनीय है। ध्यान दें कि हम अनुपात के औसत मूल्य का उपयोग नहीं कर सकते हैं, क्योंकि सामान्य मामले में यह सकारात्मक संभावना के कारण अनंत के बराबर होगा कि एक भी मूल्य वापस नहीं आएगा।