
सौ-मंजिला इमारत और दो ग्लास गेंदों का कार्य लंबे समय से इंटरनेट समुदाय को
परेशान कर रहा है (
हैब्राह ,
एलजे ,
मंचों )। जिज्ञासु मन निश्चित रूप से खुद से पूछते हैं: सामान्य मामले में क्या करना है, जब हमारे पास
एन फर्श और
के बॉल्स हैं?
मान लीजिए कि केस
n = 2
40 ,
k = 10 में कितने थ्रो (कम से कम लगभग) की आवश्यकता होगी?
नेटवर्क की विशालता और अपने स्वयं के काम पर मिली जानकारी को जोड़कर, मैं आपको इस समस्या को हल करने के लिए महत्वपूर्ण विचारों के साथ-साथ अध्ययन के दौरान प्राप्त मुख्य परिणामों और दिलचस्प टिप्पणियों के बारे में एक पोस्ट पेश करना चाहता हूं।
तो, हम इस
स्थिति को बताते
हैं : हमारे पास
कश्मीर कांच की गेंदें हैं। जब "
n " -storey घर के "
x " -th या उच्च तल से गिरते हैं, तो वे टूट जाते हैं, जब "
x - 1" -th या निचले तल से गिरते हैं - बरकरार रहते हैं।
X का मान अज्ञात है और 1 से
n तक कोई भी प्राकृतिक संख्या हो सकती है। यह आवश्यक है:
1. परीक्षण की सबसे छोटी संख्या (बॉल थ्रो) निर्धारित करें, जिसके लिए यह
एक्स (इसके मूल्य की परवाह किए बिना, हमारे लिए सबसे खराब स्थिति में) की गारंटी है।
2. एक एल्गोरिथ्म का विकास करें जो उपरोक्त परीक्षणों की संख्या से अधिक के लिए
x खोजने की गारंटी है।
कम से कम परीक्षणों की संख्या का अनुमान
दो चरम मामलों को अलग करना आसान है:
ए) हमारे पास
केवल 1 गेंद है । फिर हम इसे प्रत्येक मंजिल से बारी-बारी से फेंकना शुरू करते हैं, पहली से शुरू करते हुए, जब तक कि यह टूट न जाए या जब तक हम "
एन - 1" मंजिल तक न पहुंच जाएं। यदि बॉल "
a " फ्लोर (1 ≤
a 1
n - 1) पर दुर्घटनाग्रस्त हुई, तो
x =
a । यदि यह "
n - 1" वें में नहीं टूटता है, तो
x =
n । सबसे खराब स्थिति में,
n - 1 परीक्षण की आवश्यकता होगी।
बी) हमारे पास
कई गेंदें हैं (अर्थात्,
k have लॉग
2 एन )। फिर आप आवेदन कर सकते हैं
खोज विधि "एक खंड को आधे में विभाजित करना"हम गेंद को घर के मध्य से (फर्श से संख्या ⌉ n / 2 middle, जहां ⌉ n / 2 n n / 2 के बराबर या उससे अधिक छोटा होता है) से फेंक देते हैं। यदि यह दुर्घटनाग्रस्त नहीं होता है, तो हम इसे इमारत के ऊपरी आधे हिस्से के बीच से फेंक देते हैं, अगर यह दुर्घटनाग्रस्त हो जाता है, तो हम इमारत के निचले आधे हिस्से के बीच से दूसरी गेंद फेंकते हैं, और इसी तरह, हर बार इमारत के संबंधित हिस्से को "आधा" में विभाजित करते हैं।
सबसे खराब स्थिति में, आपको 2log
2 n and परीक्षणों और समान गेंदों की आवश्यकता होगी (अचानक उन्हें हर फेंक दिया जाएगा)।
इस प्रकार,
परीक्षणों की
सबसे छोटी संख्या nlog
2 n number से
n - 1 समावेशी तक होती है। फ़ंक्शन
f (
n ,
k ) द्वारा इस संख्या को अस्वीकार करें।
उदाहरण के लिए, एक-कहानी वाले घर और
के बॉल्स के मामले में ⌉log
2 100 7 = 7, 100 - 1 = 99, तब 7 then
f (100,
k ) case 99। सामान्यतया,
च (
n ,
k ) का मान बढ़ने के साथ बहुत जल्दी घट जाता है।
के । तो,
एफ (100, 1) = 99,
एफ (100, 2) = 14,
f (100, 3) = 9,
f (100, 4) = 8,
f (100, 5) =
f (100, 6) =
f (100, 7) = ... = 7।
एक उल्लेखनीय तथ्य: एक-कहानी वाली इमारत के मामले में, आप
केवल पाँच गेंदों के साथ सात प्रयासों में
x पा सकते हैं! यही है, "खंड को आधा में विभाजित करके" खोज विधि एक रामबाण नहीं है - यह तेज है, लेकिन आवश्यक गेंदों की संख्या के मामले में हमेशा सबसे इष्टतम नहीं है।
परीक्षणों की कम से कम संख्या की गणना के लिए पुनरावृत्ति फार्मूला
तो, आप
f (
n ,
k ) का सटीक मान कैसे पाते हैं?
सरलतम स्थितियों में, सब कुछ स्पष्ट है:
f (
n , 1) =
n - 1 (मामला A देखें),
f (
n ,
k ) = 2log
2 n ≥ for
k 2 log
2 n (मामला B देखें) संख्या
f (1,
k ) = 0 (यदि केवल एक मंजिल है, तो यह समस्या की स्थिति के अनुसार वांछित भी है)।
N and 2 और
k ose 2 के मामले पर विचार करें। मान लीजिए कि पहली परीक्षा में हमने "
a " फ्लोर से एक बॉल फेंकी, 1 से
n - 1 समावेशी हो सकती है ("
n " फ्लोर से बॉल फेंकना व्यर्थ है)। दो परिणाम संभव हैं:
निर्गमन 1: गेंद दुर्घटनाग्रस्त हो गई। इसका मतलब है कि 1 ≤
x ≤
ए । हमारे पास
एक अस्पष्टीकृत फर्श है,
k - 1 गेंदें, अर्थात।
एक्स को खोजने के लिए गारंटी दी जानी चाहिए
, एक और
एफ (
ए ,
के - 1) परीक्षण की आवश्यकता है।
निर्गमन 2: गेंद दुर्घटनाग्रस्त नहीं हुई। इसका मतलब है कि
एक + 1 a
x that
एन । हमारे पास
n है -
एक अस्पष्टीकृत फर्श,
के गोले, यानी।
एक्स को खोजने के लिए गारंटी दी जानी चाहिए
, एक और
एफ (
एन -
ए ,
के ) परीक्षण की आवश्यकता है।
नतीजतन, "
a " -th फ्लोर से बॉल फेंकने के बाद, आपको उस
x की गारंटी देने के लिए एक और अधिकतम {
f (
a ,
k - 1),
f (
n -
a ,
k )} टेस्ट की आवश्यकता हो सकती
है ।
हम परीक्षणों की संख्या को कम करना चाहते हैं, इसलिए हम ऐसा लेते हैं कि अधिकतम {
f (
a ,
k - 1),
f (
n -
a ,
k )} सबसे छोटा है, अर्थात्
एक {max {
f (
a ,
k - 1) ,
f (
n -
a ,
k )}}।
इस प्रकार,
परीक्षणों की
सबसे छोटी संख्या है :
f (
n ,
k ) = 1 + min
a {अधिकतम {
f (
a ,
k - 1),
f (
n -
a ,
k )}} (सूत्र 1)।
यह सूत्र किसी भी दिए गए
n और
k के लिए
f (
n ,
k ) और साथ ही फर्श संख्या
a (
n ,
k ) = से गणना करने के लिए पर्याप्त है, जिसमें से आप गेंद फेंकना चाहते हैं - यह उन में से कोई भी हो सकता है जिसके लिए मान अधिकतम {
f (
a ,
k - 1),
f (
n -
a ,
k )} न्यूनतम पहुँचता है।
गणना को लागू करना आसान है, उदाहरण के लिए,
एक्सेल में ।
कौन परवाह करता हैकॉलम A में, दूसरी पंक्ति से शुरू होकर, हम 1 से आवश्यक एक के क्रम में
n के मान लिखेंगे। कॉलम बी में, इसी पंक्तियों में, हम
एफ (
एन , 1) के मानों को कॉलम सी में लिखते हैं,
एफ (
एन , 2) के मूल्यों, और इसी तरह, एक कॉलम द्वारा दाईं ओर एक गेंद की संख्या में वृद्धि का मतलब है।
N = 1 के लिए, फ़ंक्शन
f (
n ,
k ) का मान शून्य है, इसलिए, हम इसी लाइन को शून्य से भरते हैं।
सेल बी 3 में, सूत्र =
ए 3 - 1,
च के बाद से (
एन , 1) =
एन - 1. कॉपी करें (या खिंचाव) वांछित संख्याओं के लिए इसे नीचे कॉपी करें।
सेल C3 में, सूत्र लिखें:
= 1 + MIN (IF (B $ 2: B2> BIGGEST (C $ 2: C2; $ A $ 2: $ A2); B $ 2: B2; BIGGEST (C $ 2: C2; $ A $ 2, $ A2)))
और
CTRL + SHIFT + ENTER दबाएँ , अर्थात सरणी सूत्र दर्ज करें। इसे नीचे पंक्तियों की वांछित संख्या और दाईं ओर कॉलम के लिए कॉपी (या खिंचाव) करें।
A (
n ,
k ) के मानों की गणना
f (
n ,
k ) की गणना करने के लिए उपयोग किए जाने वाले उन लोगों के दाईं ओर के कॉलम में की जाएगी: पंक्तियाँ
n के मान के अनुरूप होती हैं, दाईं ओर एक कॉलम द्वारा एक शिफ्ट का मतलब एक गेंद की संख्या में वृद्धि है।
स्क्रीनशॉट के रूप में स्थिति में, कॉलम एच, तीसरी पंक्ति से शुरू होता है, इकाइयों से भरा होता है, चूंकि (
एन , 1) = 1 (मामला ए देखें, हम हमेशा पहली मंजिल से केवल गेंद फेंकते हैं)।
सेल I3 में, सूत्र लिखें:
= MAX ((B $ 2: B2 <C3) * (BIGGEST (C $ 2: C2; $ A $ 2: $ A2) <C3) * $ A $ 2: $ A2)
और
CTRL + SHIFT + ENTER दबाएँ , अर्थात सरणी सूत्र दर्ज करें। इसे नीचे पंक्तियों की वांछित संख्या और दाईं ओर कॉलम के लिए कॉपी (या खिंचाव) करें।
एक्स खोज एल्गोरिथ्म
अगर हम
a (
n ,
k ) के मूल्यों को जानते हैं, तो
f (
n ,
k ) परीक्षणों से अधिक नहीं के लिए खोज एल्गोरिदम
x का वर्णन करना आसान है।
प्रवेश:
n घर के फर्श की संख्या है,
k गेंदों की संख्या है।
आउटपुट:
एक्स - वांछित मंजिल की संख्या।
एल्गोरिथ्म की शुरुआत।
चरण 1. चर को प्रारंभ करें:
x : = 1. चरण 2 पर जाएं।
चरण 2. रोक स्थिति: यदि
n = 1 है, तो आउटपुट
x और STOP, अन्यथा चरण 3 पर जाएं।
चरण 3. संख्या
x - 1 +
a (
n ,
k ) के साथ गेंद को फर्श से फेंको। यदि गेंद दुर्घटनाग्रस्त होती है, तो चर के मानों को अपडेट करें:
n : = (
n ,
k ),
k : =
k - 1।
यदि गेंद दुर्घटनाग्रस्त नहीं होती है, तो चर के मानों को अपडेट करें:
x : =
x +
a (
n ,
k ),
n : =
n - (
n ,
k )। चरण 2 पर जाएं।
एल्गोरिथ्म का अंत।
आइए एक उदाहरण देखें कि सात परीक्षणों में
x कैसे ढूंढें यदि हमारे पास एक सौ मंजिलें और पांच गेंदें हैं।
Excel में निर्मित तालिका से (
n ,
k ) के मानों का उपयोग करते हुए, हम उन मंजिलों की संख्या लिखते हैं जिनसे हम गेंद फेंकते हैं,
अगर वे हर समय टूटते हैं:
५ 11 ->
२६ ->
११ ->
४ ->
१ (यदि नहीं तोड़ा गया है) ->
२ (यदि नहीं तोड़ा है, तो) ->
३ ।
यदि, उदाहरण के लिए, 26 वीं मंजिल से गेंद फेंकने के बाद यह दुर्घटनाग्रस्त नहीं हुई, तो हम खुद को स्थिति
n = 31,
k = 4. में पाते हैं, फिर फेंकता का क्रम इस तरह दिखता है:
57 ->
26 -> 26 + 15 =
41 -> 26 + 7 =
33 -> 26 + 3 =
29 -> 26 + 1 =
27 (यदि नहीं तोड़ा गया, तो) -> 27 + 1 =
28 ।
मैं सभी संभावित विकल्पों पर विचार नहीं करूंगा। यह देखा जा सकता है कि एल्गोरिथ्म "आधे हिस्से में एक खंड को विभाजित करके" खोज विधि से अलग है।
कम से कम परीक्षणों की गणना के लिए "स्पष्ट" सूत्र
सूत्र 1 का मुख्य दोष यह है कि इसकी गणना करने में काफी संसाधन लगते हैं। मैंने फ़ंक्शन मानों की तालिका में पैटर्न की खोज और पुष्टि करके केवल
k = 2 और
k = 3 के लिए स्वयं इस पुनरावृत्ति सूत्र को स्पष्ट रूप से हल करने में कामयाब रहा। विशेष रूप से, पहले मामले में, परिणाम निम्नानुसार है:
f (
n , 2) =)

⌉।
लोगों को अन्य विचारों से समान परिणाम प्राप्त हुए:
एक लेख (लेखक -
स्टेबनाइड )। सच्चाई उसका जवाब है
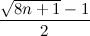
, जो समस्या की थोड़ी अलग स्थिति के कारण होता है - गेंद को ऊपर के तल से फेंकने पर तोड़ने की आवश्यकता नहीं होती है। यदि हम इस संभावना को ध्यान में रखना चाहते हैं, तो हमारे उत्तर में हमें
n (यानी, फ़र्श जोड़ें) के बजाय अभिव्यक्ति
n + 1 को प्रतिस्थापित करना होगा, और हम लेख से सूत्र प्राप्त करते हैं।
हालांकि, मैं धीरे-धीरे एक ठहराव पर आ गया, क्योंकि सामान्य सूत्र नहीं मिल सका, पुनरावृत्ति संबंध बहुत जटिल है। यह इस समय था कि मैंने
आयरिशोआक ,
बर्ट ,
मिखाइल_वीएस और अन्य के उपयोगकर्ताओं से अद्भुत विचारों की खोज की, जो हमें दिलचस्प असमानता को हल करने के लिए
f (
n ,
k ) की गणना को कम करने की अनुमति देते हैं।
ऐसा करने के लिए, हमें एक और फ़ंक्शन पर विचार करने की आवश्यकता है:
जी (
एम ,
के ) फर्श की सबसे बड़ी संख्या है, जिसके बीच आप
केएल गेंदों की उपस्थिति में
एम परीक्षण से अधिक नहीं के लिए
एक्स पा सकते हैं।
सरलतम स्थितियों में, फ़ंक्शन निम्न मान लेता है:
जी> (
m , 1) =
m + 1 (केस ए देखें),
जी (
m ,
k ) =
g (
m ,
m )
k >
m के लिए (क्योंकि
m परीक्षणों को तोड़ा जा सकता है) अधिकतम
m बॉल्स, फिर शेष
k -
m बॉल्स अनावश्यक हैं और फ़ंक्शन के मूल्य को प्रभावित नहीं करते हैं)।
M der 2,
k , 2 के लिए, हम पुनरावृत्ति सूत्र प्राप्त कर सकते हैं:
g (
m ,
k ) =
g (
m - 1,
k - 1) +
g (
m - 1,
k ) (सूत्र 2)।
निम्नलिखित तर्क से समझना आसान है:यदि हम गेंद को " ए " फ्लोर से फेंकते हैं और यह टूट जाता है, तो हमारे पास 1 से समावेशी तक की रेंज में x खोजने के लिए m - 1 प्रयास और k - 1 गेंद होगी। इसके लिए, शर्त को पूरा करना होगा: m g ( m - 1,
के - 1)। तो, उच्चतम मंजिल जिससे हम गेंद फेंक सकते हैं वह एक = जी ( एम - 1, के - 1) है। यदि यह दुर्घटनाग्रस्त नहीं होता है, तो हमारे पास m - 1 प्रयास और k बॉल्स होंगे, जिसके साथ हम एक और g ( m - 1, k ) फ़र्श का पता लगा सकते हैं। इस प्रकार, कुल जी ( m - 1, k - 1) + g ( m - 1, k ) मंजिलों का यथासंभव पता लगाना संभव होगा।
आवर्त सूत्र 2, सूत्र 1 के विपरीत, आसानी से हल हो जाता है, अर्थात। एक्सप्रेस
जी (
एम ,
के ) स्पष्ट रूप में:
g (
m ,
k ) = C
m 0 + C
m 1 + C
m 2 + ... + C
m k ,
जहाँ C
m i ,
i , C
m i =
m ! / (
i (! -
i )!) में
m के संयोजन की संख्या है।
यह समानता "रचनात्मक रूप से" काटा जा सकता है, या आप "अनुमान" कर सकते हैं और इसे प्रेरण द्वारा साबित कर सकते हैं, जो बहुत सरल है (मैं यहां प्रमाण नहीं देता)।
अब, परीक्षणों की सबसे छोटी संख्या को खोजने के लिए, आपको गणना करने की आवश्यकता है:
f (
n ,
k ) = 2log
2 n ≥ for
k , log
2 n ,
f (
n ,
k ) = min {धनात्मक पूर्णांक
m | सी <लॉग
2 एन के लिए सी
एम 0 + सी
एम 1 + सी
एम 2 + ... + सी
एम के for
एन }।
वैसे, जब
g (
m ,
k ) के लिए पुनरावृत्ति सूत्र प्राप्त करते हैं, तो एक और तरीका उस मंजिल की संख्या निर्धारित करता है जिससे आप
f (
n ,
k ) परीक्षणों की तुलना में
x को खोजने के लिए एक गेंद फेंक सकते हैं:
a (
n ,
k =
g )
एम - 1,
के - 1),
जहाँ
m =
f (
n ,
k ), अर्थात
a (
n ,
k ) = C
f ( n , k ) - 1 0 + C
f ( n , k ) - 1 1 + C
f ( n , k ) - 1 2 + ... + C
f ( n , k ) - 1 k - 1 के लिए
k <
f (
n ,
k ) (सूत्र 3),
a (
n ,
k ) = 2
f ( n , k ) - 1 for
k n f (
n ,
k ) (सूत्र 4)।
निष्कर्ष और साहसिक परीक्षण कम से कम संख्या में परीक्षण
कार्य के लिए, मैंने सहज रूप से खुद के लिए एक समाधान योजना की रूपरेखा तैयार की - पहले सही मंजिल (यानी, एक एल्गोरिथ्म विकसित करना) खोजने के सिद्धांत को समझें, फिर पता लगाएं कि सबसे खराब स्थिति में कितने फेंको की आवश्यकता होगी।
मेरे आश्चर्य के लिए, पथ अलग-अलग निकला - एक सरल एल्गोरिथ्म आसानी से छोटी संख्या में परीक्षणों की गणना के लिए सूत्रों से पीछा किया, जिसे हमने
एफ (
एन ,
के ) द्वारा निर्दिष्ट किया है।
फ़ंक्शन
च के बारे में लगभग कुछ भी नहीं जानते हुए, हमने मोटे तौर पर इसका अनुमान लगाया:
लॉग
2 एन 2 एफ (
एन ,
के ) 1
एन - 1।
हम जानते हैं कि बाईं सीमा स्पष्ट रूप से "बड़े"
k , अर्थात्
k the लॉग
2 एन , और
k = 1. के लिए दाईं ओर के लिए पहुँच गई है। हमने यह भी जाना कि
k के मध्यवर्ती मानों के
लिए खोज
f (
n ,
k ) खोजना कम कर देता है सबसे छोटा धनात्मक पूर्णांक
m (हम इसे
m 0 से निरूपित करते हैं) असमानता को संतुष्ट करते हैं:
C
m 0 + C
m 1 + C
m 2 + ... + C
m k (
n (असमानता 1)।
हालाँकि, इसे हल करने के क्रम में
f (
n ,
k ) के लिए एक स्पष्ट रूप से स्पष्ट सूत्र प्राप्त करने के लिए एक गैर-तुच्छ कार्य लगता है। आपके सुझावों को सुनना दिलचस्प होगा।
लेकिन भले ही असमानता हल नहीं हुई है, हम उस सीमा का अनुमान लगा सकते हैं जिसमें वांछित
एम 0 स्थित है, जो फ़ंक्शन का मान भी है
f (
n ,
k )।
सामान्यतया, द्विपद गुणांक के प्रस्तुत योग को चर
एम में बहुपद की डिग्री के रूप में माना जा सकता है। फिर असमानता 1 से
m 0 को कम करना, संक्षेप में, बहुपद C
0 0 + C
m 1 + C
m 2 + ... + C
m k -
n की सकारात्मक जड़ों का पता लगाना।
ऐसे तरीके हैं जो आपको बहुपद की जड़ों का मूल्यांकन करने की अनुमति देते हैं, लेकिन इसके लिए आपको इसके गुणांक जानने की जरूरत है, और हमारे मामले में वे डरावने दिखते हैं (भयानक मात्रा के माध्यम से व्यक्त किए गए तथ्य यह है कि वे गुना नहीं हैं)। इसलिए, हम अलग तरह से कार्य करेंगे।
हम दो कार्यों
h 1 (
m ,
k ) और
h 2 (
m ,
k ) का चयन करते हैं ताकि, सबसे पहले, असमानताएं
h 1 (
m ,
k )
m C
m 0 + C
m 1 + C
m 2 + ... + C
m k m h 2 (
m ,
k ), और दूसरी बात, एक निश्चित
k के लिए, असमानताएं
h 1 (
m ,
k ) and
n और
h 2 (
m ,
k ) can
n आसानी से हल की जा सकती हैं।
यह समझना आसान है कि समाधान
h 2 (
m ,
k ) give
n हमें नीचे से वांछित
m 0 का अनुमान देगा, और समाधान
h 1 (
m ,
k ) from
n ऊपर से।
द्विपद गुणांक के योग के लिए ऊपरी बाउंड के रूप में (यानी, फ़ंक्शन
एच 2 ), सबसे अच्छा परिणाम मिला
चेर्नोव की असमानता :
C
m 0 + C
m 1 + C
m 2 + ... + C
m k m 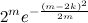
।
निर्णय
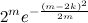
≥
n नीचे से परीक्षणों की सबसे छोटी संख्या का निम्नलिखित अनुमान देता है :
एफ (
एन ,
के ))
 k
k <के लिए
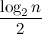
।
ईमानदारी से, मैं वास्तव में इस सूत्र को पसंद नहीं करता - यह भारी है और केवल "छोटे"
k के लिए काम करता है। लेकिन फिर भी, यह हमारे पहले - कच्चे - आकलन से बेहतर है, हालांकि हमेशा नहीं।
सामान्यतया, रेंज की निचली सीमा हमारे लिए इतनी महत्वपूर्ण नहीं होती है क्योंकि फ़ंक्शन का मान बढ़ते हुए
कश्मीर के साथ कम हो जाता है।
ऊपरी सीमा को स्पष्ट करना अधिक दिलचस्प है। ऐसा करने के लिए,
h 1 चुनें । मुझे द्विपद गुणांक के योग के लिए कम बाध्य पर कोई स्वीकार्य परिणाम नहीं मिला। कुछ का आविष्कार करने के लिए खुद का प्रयास एक अजीब स्थिति का कारण बना।
यह सोचकर, मैं इस निष्कर्ष पर पहुंचा कि C
m i to
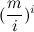 m
m ≥
i । 1 के लिए।
बाद में, मुझे तर्क में एक गलती मिली, लेकिन असमानता अभी भी मुझे सच लगती है, और एक सभ्य मार्जिन के साथ (जैसा कि संख्यात्मक प्रयोगों द्वारा दिखाया गया है)।
यह और भी महत्वपूर्ण है कि असमानता स्वयं पूरी नहीं होती है, लेकिन

≤ C
m 0 + C
m 1 + C
m 2 + ... + C
m k , जो और भी अधिक संभावना है।
दुर्भाग्य से, यह औपचारिक रूप से अभी तक सिद्ध नहीं हुआ है, मैं विचारोत्तेजक विचारों या लिंक, और संभवतः प्रतिपक्षों के लिए आभारी रहूंगा।
अंत में, मैंने इस अध्ययन को जारी रखने का फैसला किया, इस धारणा के आधार पर कि मेरी परिकल्पना सच है, इसलिए मैं परिणामी मूल्यांकन को साहसिक कहता हूं।
तो
एच 1 (
एम ,
के ) =

।
असमानता
h 1 (
m ,
k ) also
n को हल करना भी आवश्यक नहीं है। हम
m की शक्तियों के गुणांक को जानते हैं, इसलिए हम बहुपद
h 1 (
m ,
k -
n ) की जड़ों का अनुमान लगा सकते हैं।
मैक्लॉरिन अनुमान का उपयोग करते हुए, हम पाते हैं कि इसकी सभी सकारात्मक जड़ें अधिक नहीं हैं
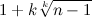
।
इसका मतलब है कि वांछित
एम 0 ≤
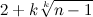
(रेटिंग 2)।
मेरी राय में, सूत्र बहुत सुंदर है - कॉम्पैक्ट, एक दिलचस्प तरीके से दोनों चर पर निर्भर करता है और, सबसे महत्वपूर्ण बात, यह सीमा को अच्छी तरह से बताता है।
ऊपर से
f (
n ,
k ) का अनुमान लगाने का एक और तरीका यह है कि इसे
f (
n , 2) = (तक सीमित किया जाए।

⌉। इस तथ्य के बावजूद कि इस सूत्र में गेंदों की संख्या पर ध्यान नहीं दिया जाता है, कभी-कभी यह 2 के स्कोर की तुलना में अभी भी बेहतर परिणाम देता है।
सुनिश्चित करने के लिए,
हम ऊपर से सबसे छोटी संख्या के परीक्षण का निम्नलिखित अनुमान लिख सकते हैं :
f (
n ,
k )) मिनट {
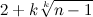
।

+ 1}।
प्राप्त सूत्रों को व्यवहार में लाते हुए, हम उदाहरण के लिए,
f (400, 4) 9 से 19 की सीमा में रखते हैं, जिसका वास्तविक मान 11. है। इसके अलावा, यह अनुमान 2 है जो सीमा की सही सीमा देता है, जबकि
f (400, 2) = 28।
अधिक चरम मूल्यों के लिए, उदाहरण के लिए,
n = 2
40 ,
k = 10, हमें बाईं सीमा मिलती है - 58, दाएं - 162. तुलना के लिए: लॉग
2 एन = 40,
एफ (
एन , 2) = 1482910, अर्थात, अनुमान 1 और विशेष रूप से 2 ने काफी अच्छा काम किया। असमानता 1 को हल करके सटीक मूल्य पाया जा सकता है, गणना 76 जवाब देती है।
निष्कर्ष
उपरोक्त सभी को देखते हुए, यह कहा जा सकता है कि सामान्य रूप से हल की गई दो ग्लास गेंदों की समस्या सामान्य है।
यद्यपि सबसे कम संख्या में परीक्षणों के लिए एक स्पष्ट सूत्र प्राप्त नहीं किया गया है, यह संपूर्ण खोज या अन्य तरीकों से असमानता 1 को हल करके निर्धारित किया जा सकता है।
सूत्रों 3 और 4 को देखते हुए, यह वांछित मंजिल को खोजने के लिए एक साधारण एल्गोरिथ्म के संचालन के लिए भी पर्याप्त है।
विश्लेषणात्मक गणना (ग्रेड 1 और 2) उस सीमा को काफी कम कर सकती है जिसमें सबसे छोटी संख्या में परीक्षण स्थित हैं, जो उन मामलों में उपयोगी हो सकता है जहां सटीक मूल्य की गणना बहुत समय लेने वाली है या आवश्यक नहीं है।
पुनश्च: जिस समय तक पोस्ट प्रकाशित हुआ था, तब तक मैं उस परिकल्पना को साबित करने में सक्षम था जिसका उपयोग मैंने 2, अर्थात्:
C
m i ≥
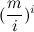 m
m ≥
i । 1 के लिए।
इसलिए, मूल्यांकन अब पूरा हो गया है, साहसी नहीं।
उसी समय,
मैं अभी भी साहित्य के संदर्भों के लिए
आभारी रहूंगा , जहां द्विपद गुणांक या उनके योगों के लिए कम सीमाएं मानी जाती हैं।
महत्वपूर्ण UPD: समस्या की चर्चा के दौरान, उपयोगकर्ता
grechnik ने द्विपद गुणांक के योग के लिए निम्न और ऊपरी सीमा का अपना संस्करण प्रस्तावित किया:
h 1 (
m ,
k ) =
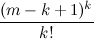
और
एच 2 (
एम ,
के ) =
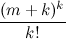
।
हमें समझाता हूँहम दिखाते हैं कि
h 1 (
m ,
k )
0 C
m 0 + C
m 1 + C
m 2 + ... + C
m k m h 2 (
m ,
k )। यह असमानताओं की श्रृंखला से होता है:
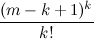
≤

= C
m k m C
m 0 + C
m 1 + C
m 2 + ... + C
m k + 1 +
m +
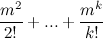
≤
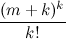
।
अंतिम असमानता सच है, क्योंकि बाईं ओर
मीटर की शक्तियों के लिए गुणांक दाईं ओर से अधिक नहीं हैं (बाईं ओर
एम एल के लिए, गुणांक है

, और दाईं ओर:
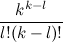
)।
अब आप निम्न
परीक्षणों की संख्या का मूल्यांकन कर सकते हैं:

-
के ≤
च (
एन ,
के ) (

+
के ।
इसका मतलब यह है कि
परीक्षणों की
सबसे छोटी संख्या है 
प्लस / माइनस की सटीकता के साथ गेंदों की संख्या के बराबर संख्या! वाह, ज़बरदस्त फॉर्मूला!
टिप्पणियों में,
grechnik और
Mrrl उपयोगकर्ता भी
f (
n ,
k ) के मूल्य के दिलचस्प
असममित अनुमान प्रदान करते हैं।