पोइंकेयर अनुमान पर। यैंडेक्स में व्याख्यान

यह 19 वीं शताब्दी में पहले से ही ज्ञात था कि यदि दो आयामी सतह पर पड़े किसी बंद लूप को एक बिंदु पर एक साथ खींचा जा सकता है, तो ऐसी सतह को आसानी से एक गोले में बदल दिया जा सकता है। तो, गुब्बारे की सतह को एक गोले में तब्दील किया जा सकता है, लेकिन डोनट की सतह नहीं है (लूप की कल्पना करना आसान है, जो डोनट के मामले में एक बिंदु तक नहीं फैलता है)। 1904 में फ्रांसीसी गणितज्ञ हेनरी पोनकारे ने कहा था कि इस तरह का बयान तीन आयामी अभिव्यक्तियों के लिए है।

पोंकारे केवल परिकल्पना को 2003 में साबित करने में सक्षम थे। इसका प्रमाण हमारे हमवतन ग्रेगरी पेरेलमैन से है। यह व्याख्यान एक परिकल्पना के निर्माण के लिए आवश्यक वस्तुओं पर प्रकाश डालता है, सबूतों की खोज का इतिहास और इसके मुख्य विचार।



मास्को राज्य विश्वविद्यालय के यांत्रिकी और गणित संकाय के एसोसिएट प्रोफेसरों द्वारा एक व्याख्यान दिया जाता है एन। अलेक्जेंडर झेजलोव और पीएच.डी. एन। फेडर पॉपेलेंस्की।

यदि आप गणितीय विवरणों में नहीं जाते हैं, तो पॉइंकेयर परिकल्पना द्वारा उठाए गए प्रश्न निम्नानुसार हो सकते हैं: (तीन-आयामी) क्षेत्र को कैसे चिह्नित किया जाए? इस प्रश्न को सही ढंग से समझने के लिए, आपको टोपोलॉजी - होमियोमॉर्फिज़्म में सबसे महत्वपूर्ण अवधारणाओं में से एक से परिचित होने की आवश्यकता है। इससे निपटने के बाद, हम सही ढंग से पॉइंकेयर अनुमान प्रस्तुत कर सकते हैं।



औपचारिक परिभाषा के गणितीय विवरणों में बिल्कुल भी शामिल नहीं होने के लिए, हम कहेंगे कि दो आंकड़ों को होमोमोर्फिक माना जाता है यदि इन आंकड़ों के बिंदुओं के बीच एक से एक-एक पत्राचार स्थापित करना संभव है, जिस पर एक आंकड़े के करीबी बिंदु दूसरे आंकड़े के करीबी बिंदुओं के विपरीत होते हैं और इसके विपरीत। जिन विवरणों को हमने छोड़ा था, उनमें अंकों की निकटता की पर्याप्त औपचारिकता होती है।

यह समझना आसान है कि दो आंकड़े होमियोमॉर्फिक हैं यदि दूसरे में से एक मनमाना विरूपण द्वारा प्राप्त किया जा सकता है, जिसमें सतह को "खराब" करना (एक बिंदु पर क्षेत्र को क्रश करना, छेद करना, छेद करना आदि) करने से मना किया जाता है।



उदाहरण के लिए, एक डिस्क से एक गोलार्ध प्राप्त करने के लिए, जैसा कि ऊपर की तस्वीर में दिखाया गया है, हमें बस बाहरी केंद्र से पकड़े हुए, ऊपर से इसके केंद्र तक प्रेस करने की आवश्यकता है। आप कल्पना कर सकते हैं कि सतहों को सही रबर से बनाया गया है, ताकि सभी आकार को संकुचित और बढ़ाया जा सके जैसा आप चाहें। आप केवल दो काम नहीं कर सकते हैं: आंसू और गोंद।



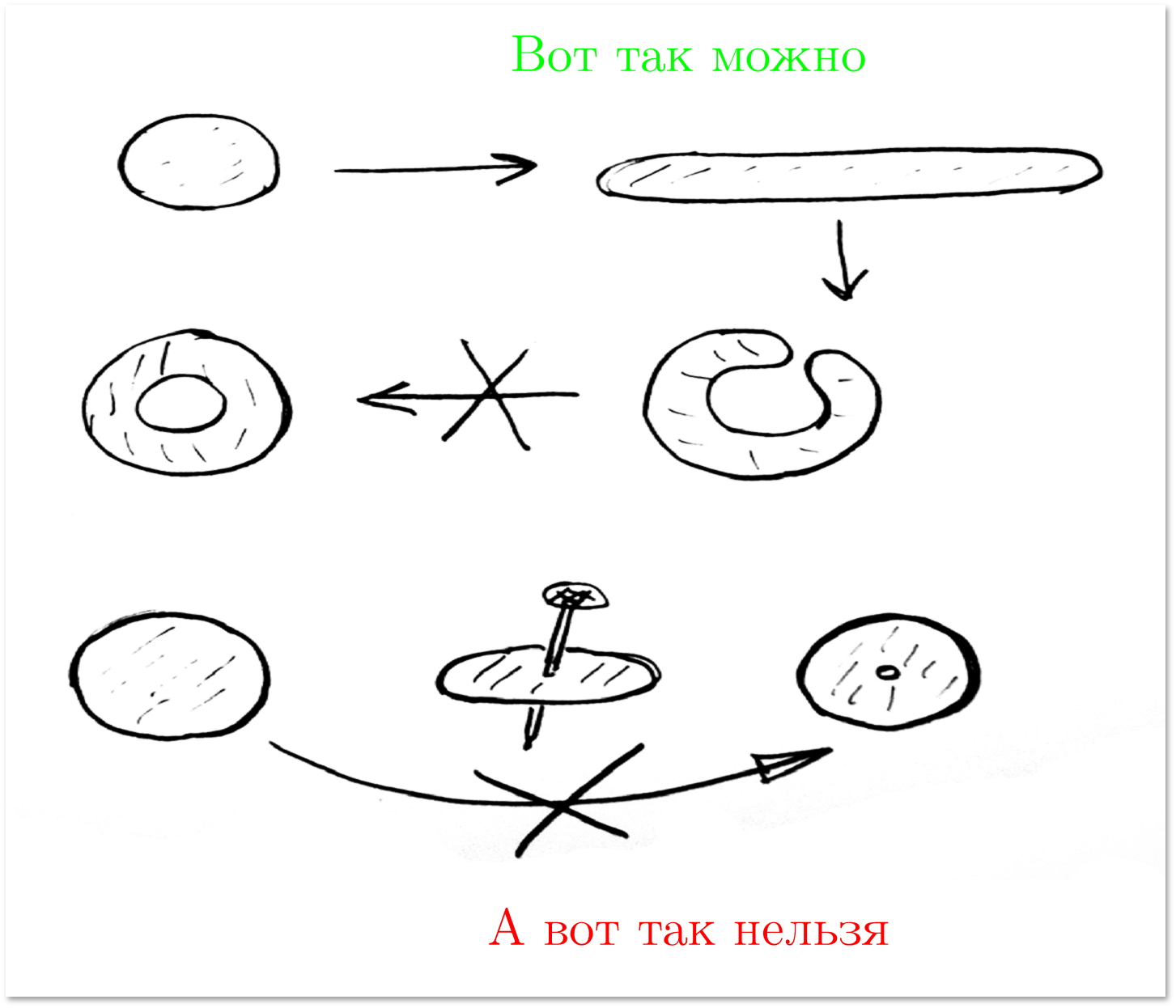
यदि हम एक और ऑपरेशन की अनुमति देते हैं, तो हम एक अधिक सटीक (लेकिन अभी भी कठोरता के दृष्टिकोण से अंतिम नहीं) होमोमोर्फिक आंकड़ों के बारे में विचार करेंगे: हम आकृति, मोड़, टाई, यूटीआई आदि पर कटौती कर सकते हैं, लेकिन फिर कटौती को सील करना आवश्यक है। यह किया गया था।



हम एक और उदाहरण देते हैं। एक सेब की कल्पना करें जिसमें एक कीड़ा एक गाँठ और एक छोटी गुफा के रूप में एक मार्ग से गुजरता है।



टोपोलॉजी की दृष्टि से, इस सेब की सतह अभी भी एक क्षेत्र है, क्योंकि यदि हम इसे एक निश्चित तरीके से खींचते हैं, तो हमें सेब की सतह उसी रूप में मिलती है जैसे कि कीड़ा इसे खाने से पहले था।

समेकित करने के लिए, लैटिन वर्णमाला के अक्षरों को होमोमोर्फिज्म तक वर्गीकृत करने का प्रयास करें (यानी यह पता करें कि कौन से अक्षर होमोमोर्फिक हैं और जो नहीं हैं)। उत्तर अक्षरों की शैली पर निर्भर करता है (फ़ॉन्ट के प्रकार पर या टाइपफेस पर निर्भर करता है), और शैली के सबसे सरल संस्करण के लिए यह निम्न आकृति में दिखाया गया है:



26 अक्षरों से हमें केवल 8 कक्षाएं मिलती हैं।

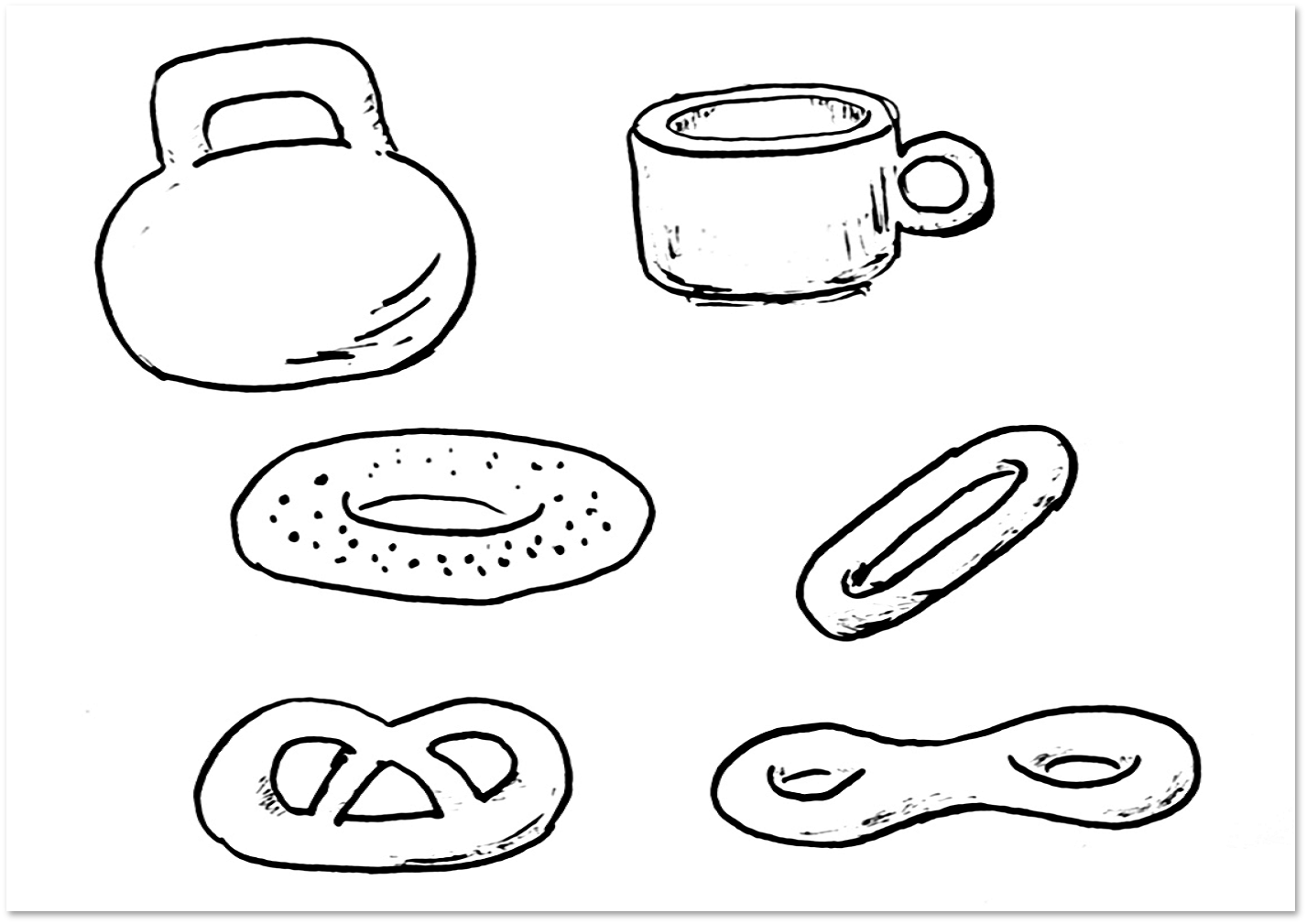
निम्नलिखित चित्र केतलीबेल, कॉफी कप, बैगेल, ड्रायर और प्रेट्ज़ेल को दर्शाता है। एक टोपोलॉजिकल दृष्टिकोण से, वजन, कॉफी कप, बैगल्स और सुखाने की सतह समान हैं, अर्थात। होमियोमॉर्फिक। प्रेट्ज़ेल के लिए, यह सतह के साथ तुलना के लिए यहां दिया गया है, जिसे टोपोलॉजी में अक्सर प्रेट्ज़ेल कहा जाता है (इसे आंकड़े के निचले दाएं कोने में दर्शाया गया है)। जैसा कि आप शायद पहले से ही समझते हैं, दोनों टोपोलॉजिकल प्रेट्ज़ेल और खाद्य प्रेट्ज़ेल दोनों टोरस से अलग हैं।

औपचारिक प्रश्न

आज्ञा देना एम बंद आयाम से जुड़ा हुआ है 3. चलो किसी भी लूप को एक बिंदु पर अनुबंधित किया जाए। तब M एक त्रि-आयामी क्षेत्र में होमोमोर्फिक है।

यहां एक अप्रशिक्षित व्यक्ति के लिए सबसे बड़ी कठिनाई "आयाम 3 के कई गुना" और "बंद" और "कनेक्टेड" शब्दों द्वारा व्यक्त किए गए गुणों की अवधारणा है। इसलिए, हम आयाम 2 के उदाहरण का उपयोग करके इन सभी अवधारणाओं और गुणों से निपटने की कोशिश करेंगे; इस मामले में, बहुत मौलिक रूप से सरलीकृत किया गया है।

सतहों के लिए Poincare अनुमान

आज्ञा देना एक बंद सतह (आयाम 2 के कई गुना)। इस पर किसी भी लूप को एक बिंदु पर खींचने दें। फिर सतह M एक द्वि-आयामी क्षेत्र में होमोमोर्फिक है।

पहले हम परिभाषित करते हैं कि सतह क्या है। बहुभुजों का एक छोटा सेट लें, उनके सभी पक्षों (किनारों) को जोड़े में विभाजित करें (यानी, सभी बहुभुजों के सभी पक्षों में एक समान संख्या होनी चाहिए), प्रत्येक जोड़ी में हम चुनते हैं कि हम उन दो संभावित तरीकों में से कौन सा उन्हें गोंद करेंगे। हम गोंद करते हैं। नतीजतन, एक बंद सतह सीखी जाती है।

यदि परिणामस्वरूप सतह में एक टुकड़ा होता है, और कई अलग नहीं होते हैं, तो वे कहते हैं कि सतह जुड़ा हुआ है। औपचारिक दृष्टिकोण से, इसका मतलब है कि किसी भी बहुभुज के किसी भी शीर्ष से gluing के बाद, आप किनारों के साथ किसी भी शीर्ष शीर्ष पर जा सकते हैं।



यहां एक सरल उदाहरण है: यदि हम मानते हैं कि ऊपर की तस्वीर में सभी त्रिकोण सही हैं, तो एक साथ gluing के बाद हमें एक नियमित टेट्राहेड्रॉन मिलना चाहिए जिसकी सतह भी गोले के लिए होमोमोर्फिक है।

औपचारिक रूप से, आपको यह आवश्यकता है कि किसी भी बहुभुज के किसी भी शीर्ष से gluing के बाद किसी भी बहुभुज (किनारों के साथ) के किसी भी शीर्ष पर जाना संभव है।

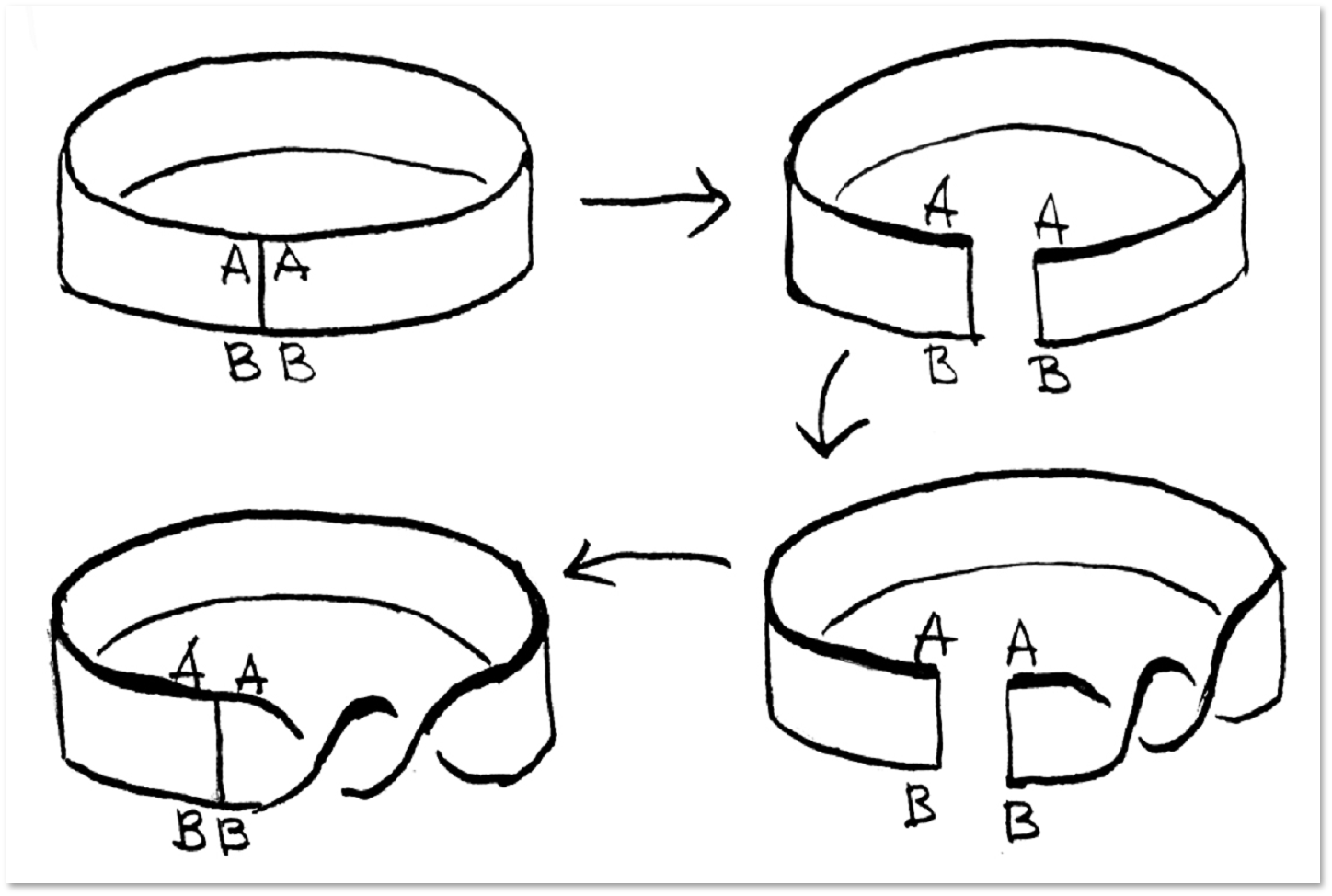
यह देखना आसान है कि एक जुड़े सतह को एक बहुभुज से भी चिपकाया जा सकता है। आंकड़ा यह दर्शाता है कि यह कैसे उचित है:



सरल glues के उदाहरणों पर विचार करें:



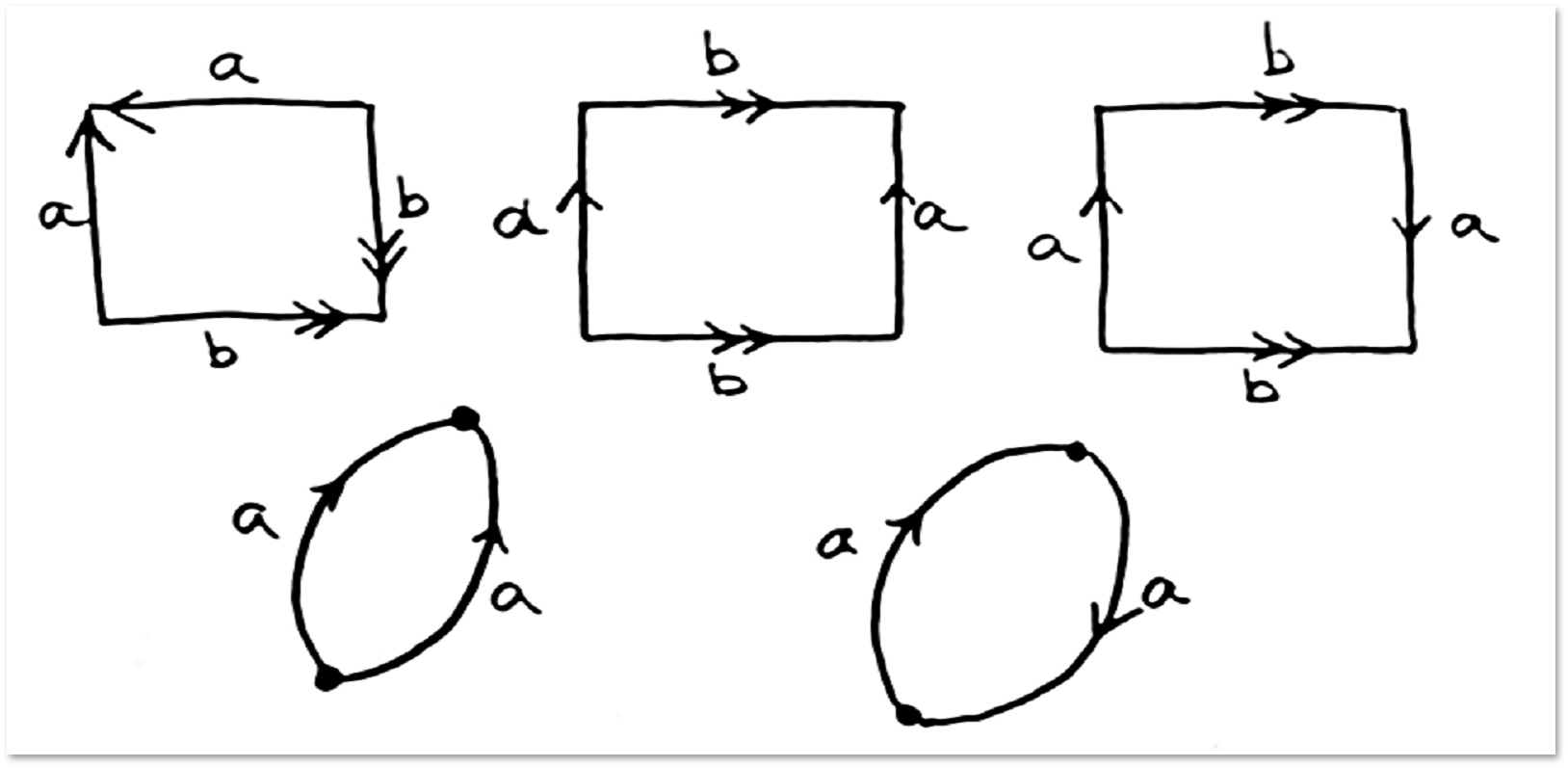
पहले मामले में, हमें क्षेत्र मिलता है:



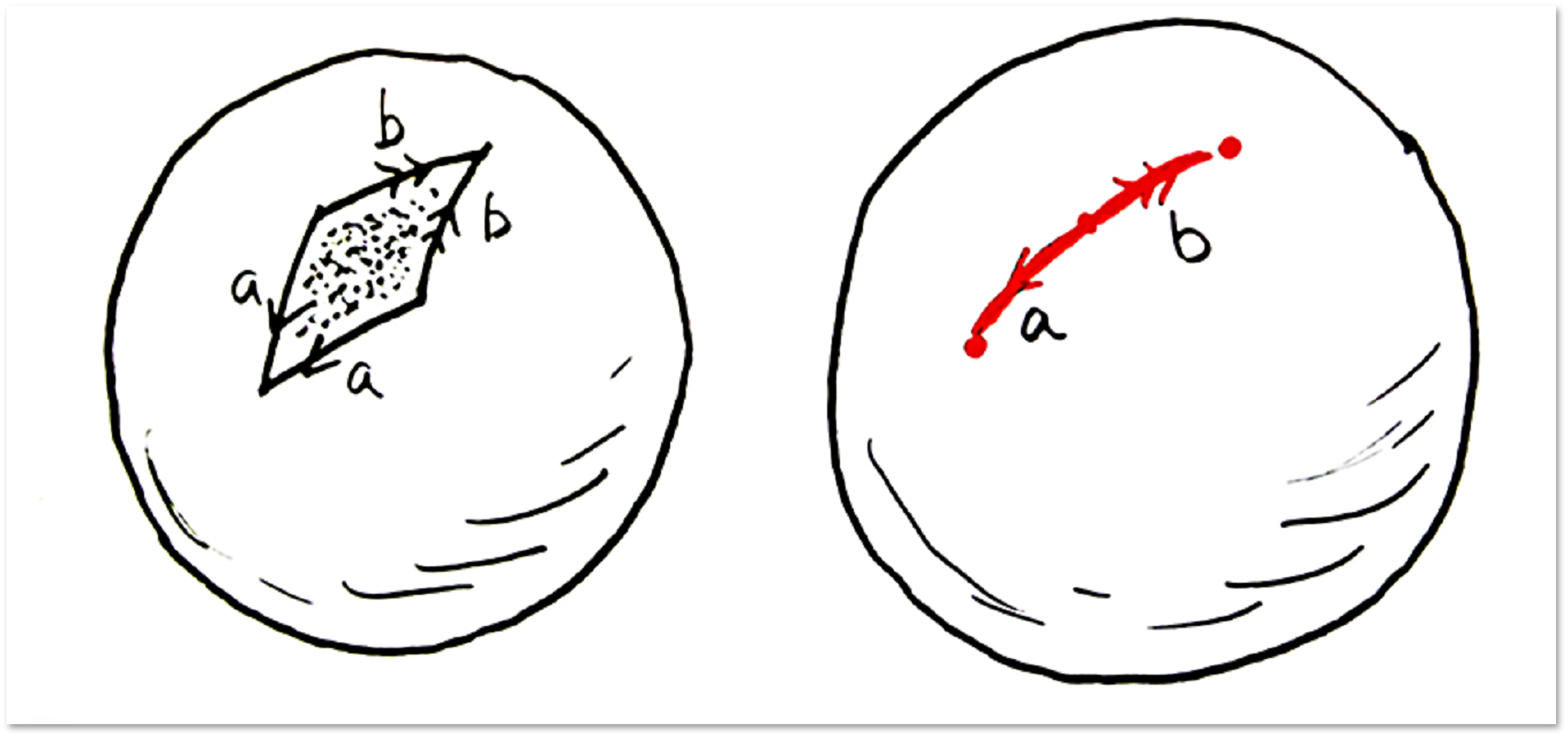
दूसरे मामले में, हमें एक टोरस (डोनट सतह मिलती है, हम इसके साथ पहले मिले थे):



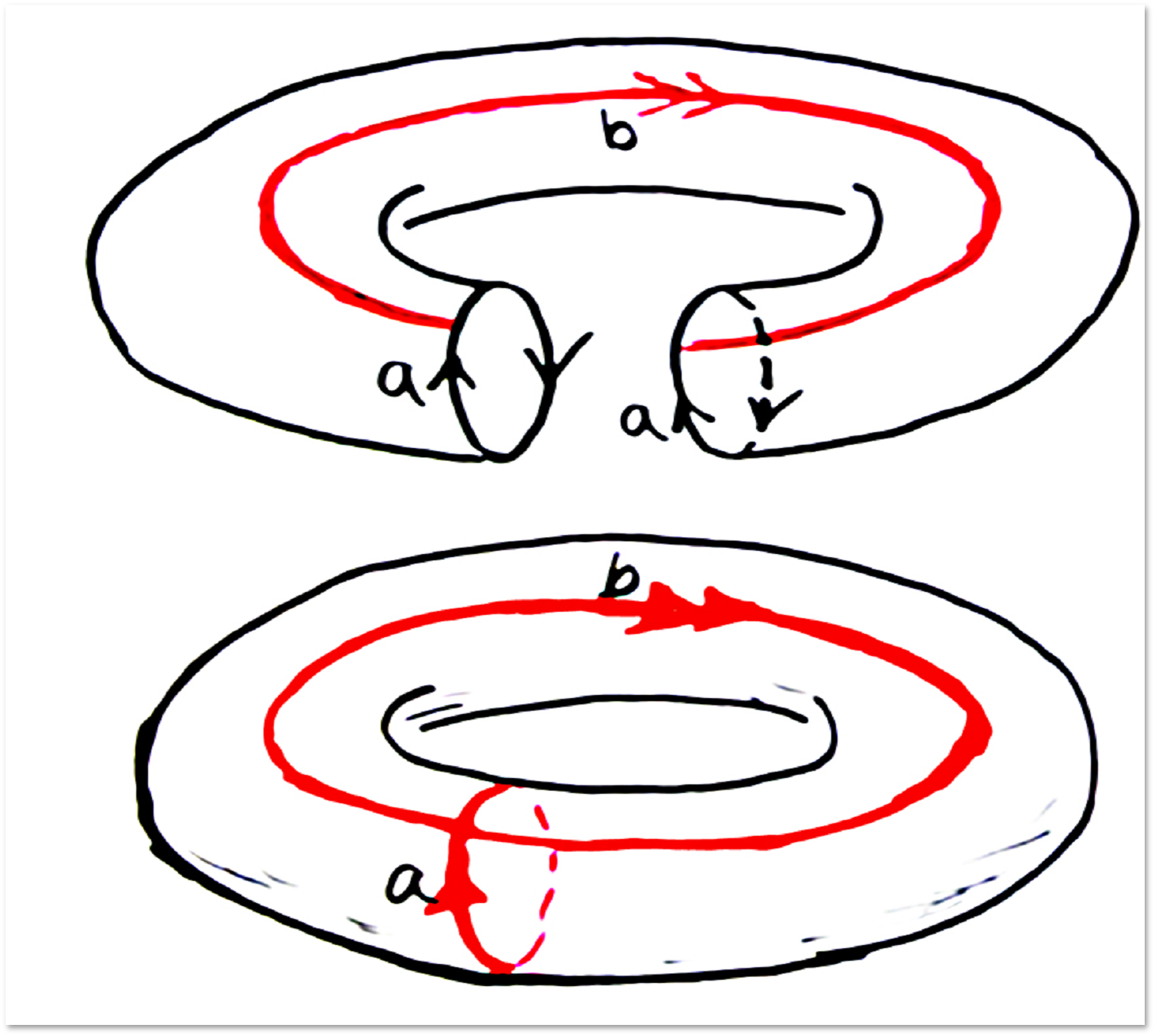
तीसरे मामले में, हमें तथाकथित क्लेन बोतल मिलती है:



यदि बहुभुज के सभी पक्षों को एक साथ सरेस से जोड़ा हुआ नहीं है, तो हमें किनारे के साथ एक सतह मिलती है:



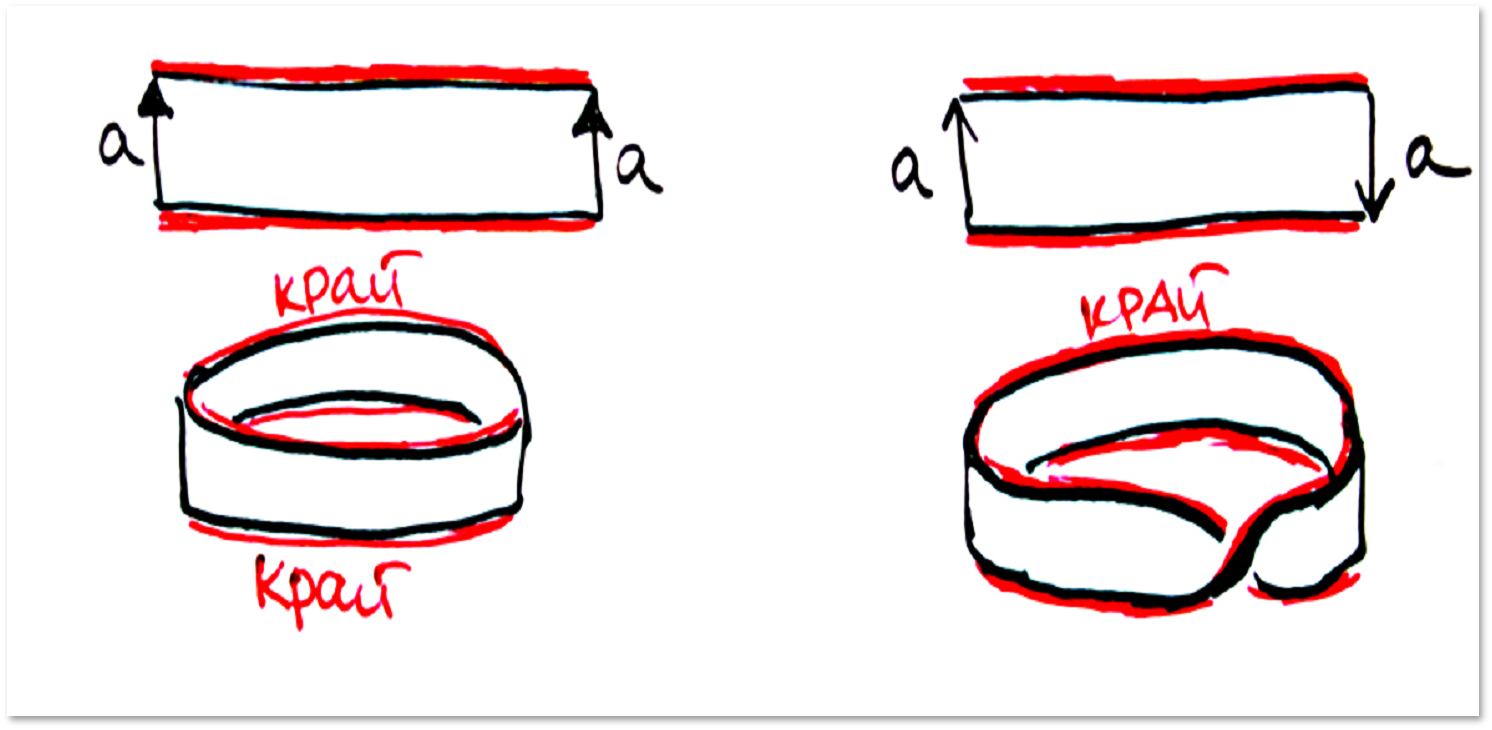
यह ध्यान रखना महत्वपूर्ण है कि "निशान" को चमकाने के बाद यह पूरी तरह से प्रकृति में "कॉस्मेटिक" है। सतह पर सभी बिंदु समान हैं: किसी भी बिंदु में डिस्क के लिए एक पड़ोसी होमियोमॉर्फिक है।

दो सतहों को होमोमोर्फिक माना जाता है यदि उनमें से प्रत्येक के ग्लूइंग पैटर्न को छोटे बहुभुजों के ग्लूइंग पैटर्न में इतना काट दिया जाए कि ग्लूइंग पैटर्न समान हो जाए।

आइए इस कथन का विश्लेषण करें कि क्यूब की सतह को भागों में विभाजित करने के उदाहरण से आप टेट्राह्रोन का स्कैन जोड़ सकते हैं:



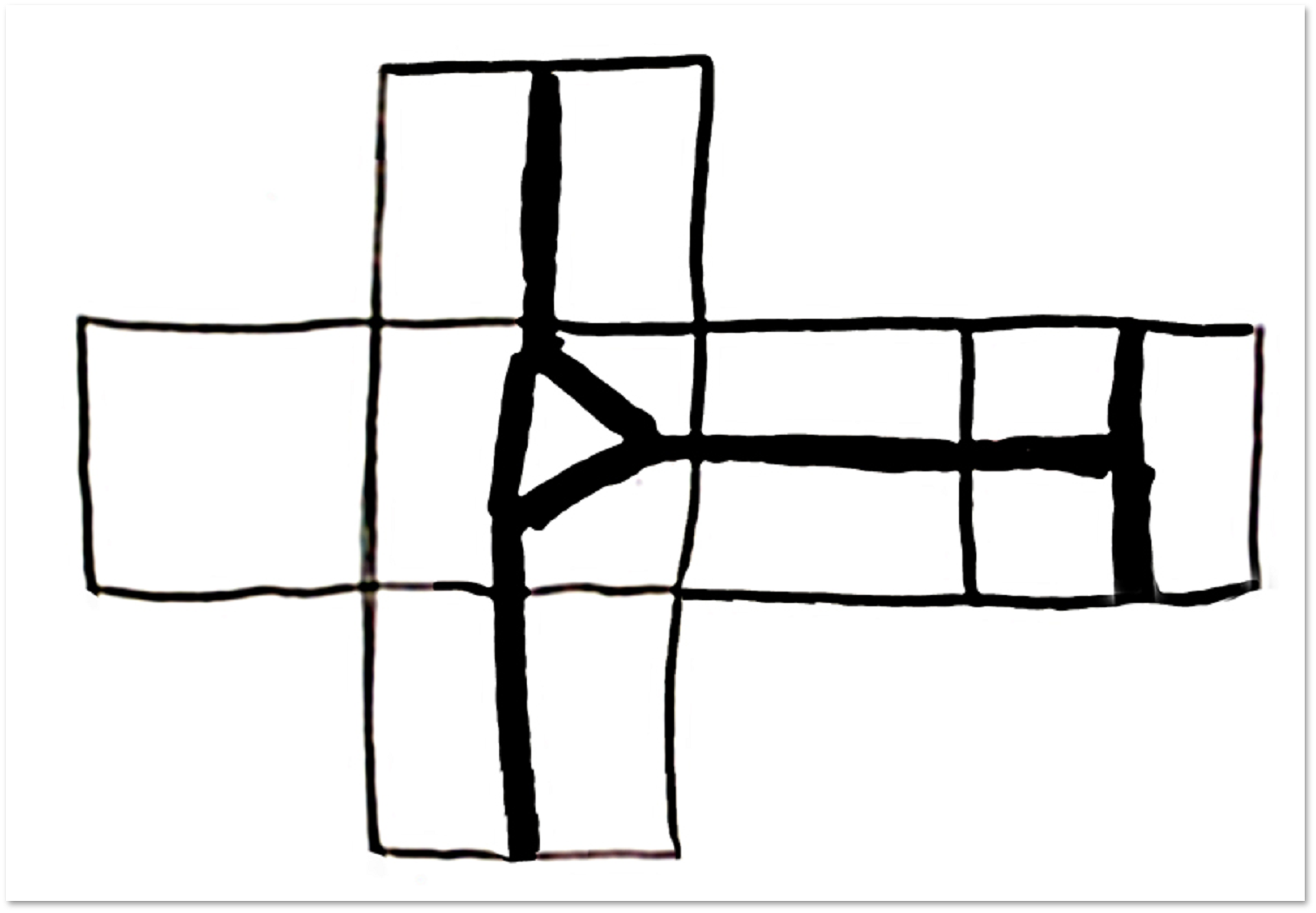
एक अधिक सामान्य तथ्य यह भी सच है: सभी उत्तल पॉलीहेड्रा की सतह गोलाकार होती हैं।

अब चलो एक लूप की अवधारणा पर ध्यान केंद्रित करते हैं। पंखुड़ी विचाराधीन सतह पर एक बंद वक्र है। दो छोरों को होमोटोपिक कहा जाता है यदि उनमें से एक को बिना फाड़ और ग्लूइंग के सतह पर शेष के रूप में विकृत किया जा सकता है। विमान या गोले पर एक लूप को अनुबंधित करने का सबसे सरल मामला निम्नलिखित है:



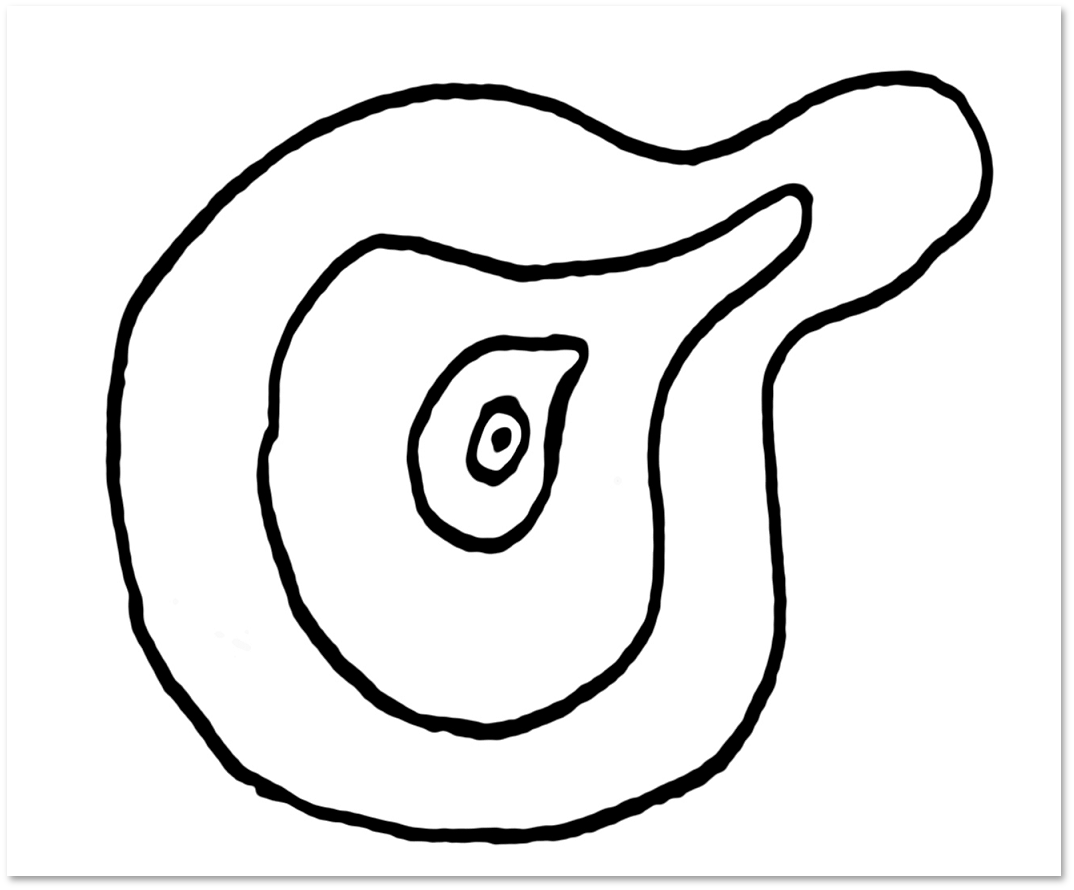
यहां तक ​​कि अगर विमान या क्षेत्र में पाश में आत्म-चौराहे हैं, तो भी इसे एक साथ खींचा जा सकता है:



विमान पर, आप किसी भी लूप को कस सकते हैं:



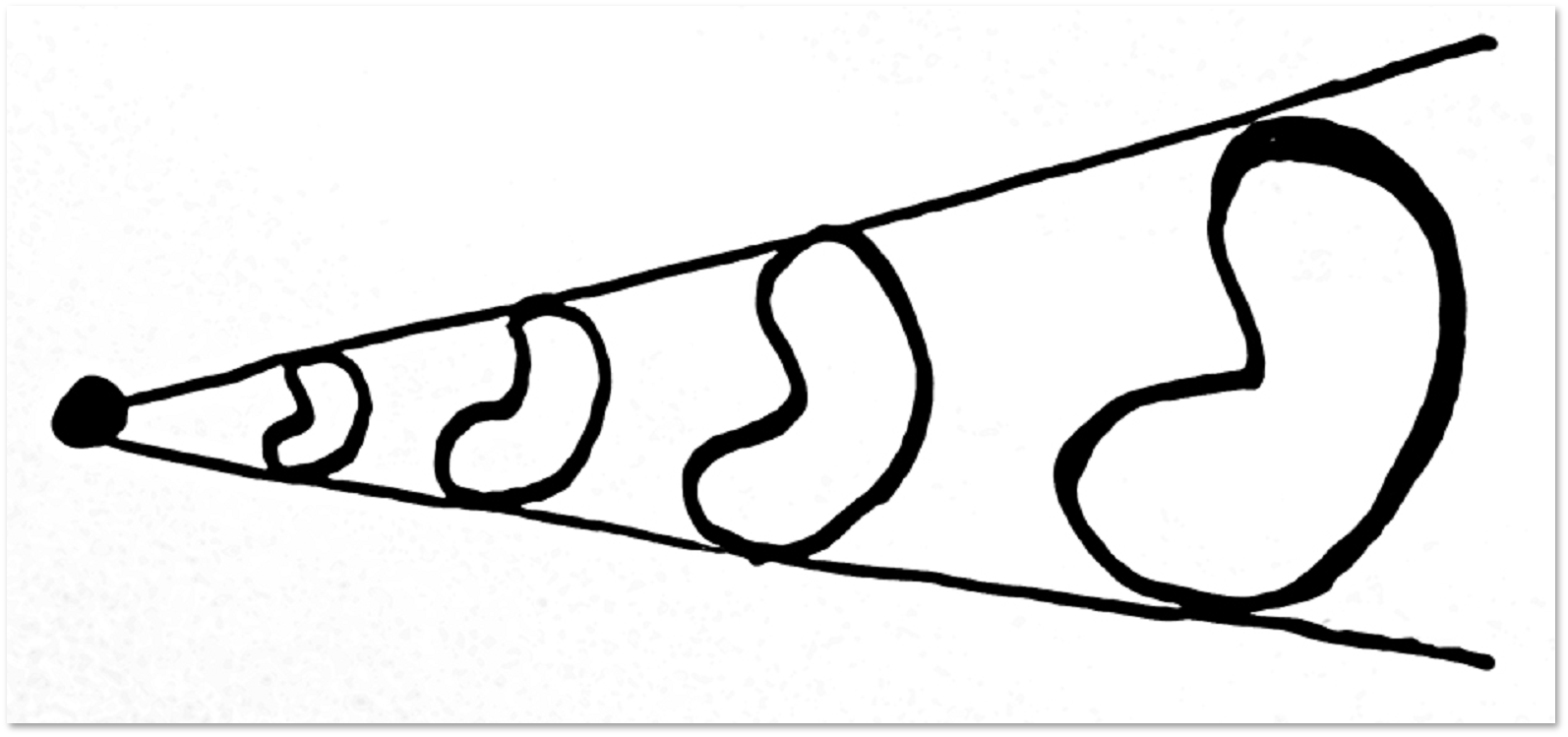
लेकिन क्या धार पर कर रहे हैं:



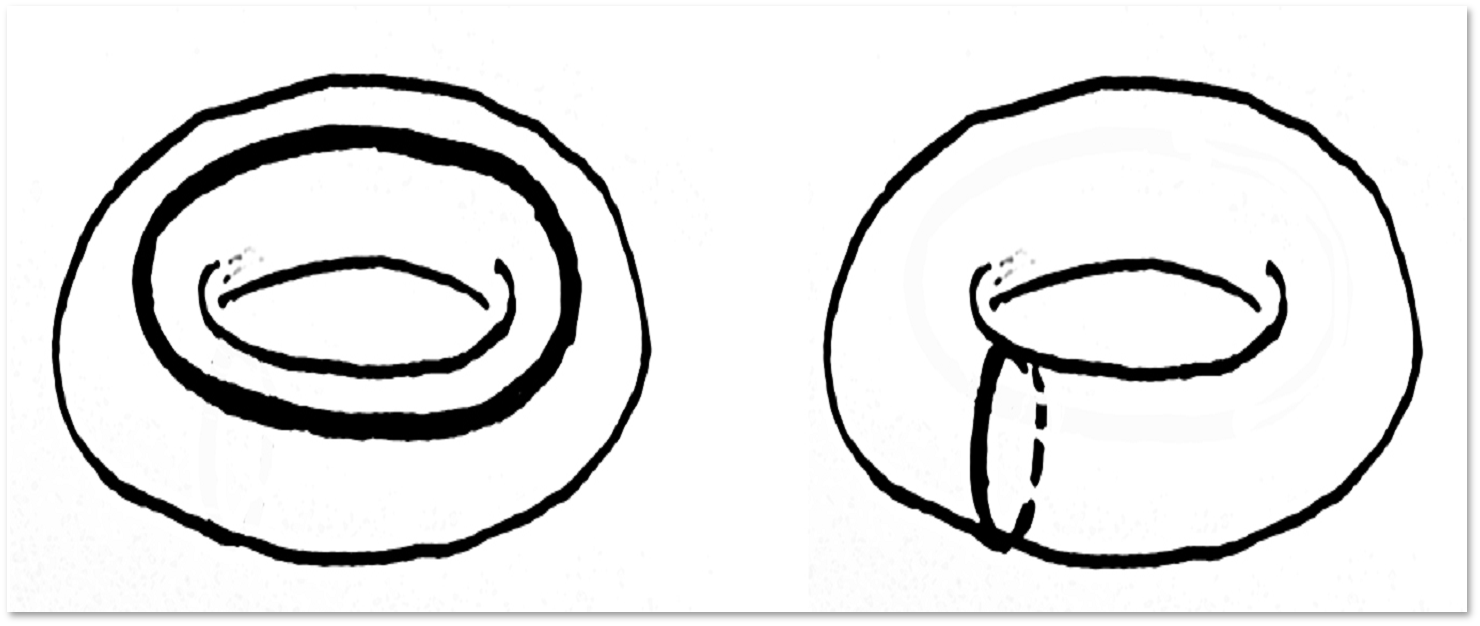
ऐसे छोरों को कसने के लिए असंभव है। (दुर्भाग्य से, सबूत हमारी कहानी के दायरे से काफी परे है।) इसके अलावा, टोरस पर दिखाए गए लूप होमोटोपिक नहीं हैं। हम सुझाव देते हैं कि श्रोताओं या पाठकों को टोरस पर एक और लूप मिलता है जो इन दोनों के लिए होमोटॉपिक नहीं है - यह एक बहुत ही सरल प्रश्न है। उसके बाद, टोरस पर चौथा लूप खोजने की कोशिश करें जो इन तीनों के लिए होमोटॉपिक नहीं है - यह कुछ अधिक जटिल होगा।

यूलर की विशेषता

अब जब हम Poincare अनुमान के निर्माण से सभी मूल अवधारणाओं से परिचित हो गए हैं, तो हम दो-आयामी मामले को साबित करने की कोशिश करेंगे (एक बार फिर, हम ध्यान दें कि यह त्रि-आयामी मामले की तुलना में कई गुना सरल है)। और यूलरियन की विशेषता हमें इसमें मदद करेगी।

एक सतह M की Euler विशेषता B - P + a की संख्या है। यहाँ G बहुभुज की संख्या है, P ग्लूइंग के बाद किनारों की संख्या है (विचाराधीन सतहों के मामले में, यह सभी बहुभुजों के पक्षों की आधी संख्या है), बी वर्टिस की संख्या है जो ग्लूइंग के बाद ग्लूइंग के बाद प्राप्त होती है।

यदि दो ग्लूइंग स्कीम्स होमोमोर्फिक सतहों को परिभाषित करती हैं, तो इन योजनाओं के लिए B - P + P की संख्या समान है, अर्थात B - P + सतह का एक व्युत्क्रम है।

यदि सतह पहले से ही किसी तरह से परिभाषित है, तो आपको उस पर किसी तरह का ग्राफ खींचने की जरूरत है ताकि उसके साथ कटने के बाद सतह डिस्क के लिए होम्योमोर्फिक के टुकड़ों में विभाजित हो जाए (उदाहरण के लिए, छल्ले निषिद्ध हैं)। तब हम बी - पी + जी - मूल्य की गणना करते हैं - यह सतह की यूलर विशेषता है।

क्या एक ही यूलर विशेषताओं वाले सतहों को होमियोमॉर्फिक किया जाएगा, हम बाद में सीखेंगे। लेकिन यह निश्चित रूप से कहा जा सकता है कि यदि सतहों की यूलर विशेषताएं अलग-अलग हैं, तो सतहों होमियोमॉर्फिक नहीं हैं।

उत्तल बहुभुज (यूलर प्रमेय) के लिए प्रसिद्ध संबंध बी - पी + 2 = 2 इस प्रमेय का एक विशेष मामला है। इस मामले में, हम एक विशिष्ट सतह के बारे में बात कर रहे हैं - एक गोला। टिप्पणी पदनाम: हम ark (M): χ (M) = B - P + - द्वारा एक सतह M की Euler विशेषता का निरूपण करते हैं।

यदि सतह M जुड़ा हुआ है, तो χ (M) and 2, और M (M) = 2 यदि और केवल यदि M गोले के लिए होमियोमॉर्फिक है।

व्याख्यान को अंत तक देखने के बाद, आप सीखेंगे कि कैसे आयाम 2 में पॉइंकेयर अनुमान को फिर भी साबित किया गया है, और ग्रिगोरी पेरेलमैन इसे आयाम 3 में कैसे साबित करने में कामयाब रहे।