🤛🏾 🏻 🤸🏽 एईएस 128। अजगर में विवरण और कार्यान्वयन 🎸 📷 🙇🏾

अपने लिए कुछ एन्क्रिप्ट करने का विचार तुच्छ रूप से पैदा हुआ था - मुझे एक और डेबिट कार्ड प्राप्त करना था और इसलिए, मेरे सिर में एक और पिन कोड रखें। व्यामोह इस तरह की जानकारी को खुले रूप में संग्रहीत करने की अनुमति नहीं देता है, यह तीसरे पक्ष की सेवाओं का उपयोग नहीं करता है, इसलिए कुछ खोजों के बाद मैं एईएस मानक पर बस गया। मैं तुरंत अतिरिक्त मॉड्यूल का सहारा लिए बिना एल्गोरिथम को समझना और लागू करना चाहता था।

लेख में मैं एल्गोरिथ्म के घटकों के बारे में विस्तार से बताऊंगा, चटाई वाले हिस्से में थोड़ा गोता लगाने और अजगर में एक उदाहरण कार्यान्वयन। विकास में, मैंने खुद को केवल वही तक सीमित किया जो मानक पुस्तकालय का हिस्सा है।

थोड़ा सा परिचय

एडवांस्ड एन्क्रिप्शन स्टैंडर्ड रिजेंडेल एल्गोरिथ्म ([r Standardindaːl]) का जाना-माना नाम है, जिसे बेल्जियम के दो क्रिप्टोग्राफर जोन डिमन और विंसेंट रेमैन ने विकसित किया था। एल्गोरिदम अवरुद्ध और सममित है। अमेरिकी सरकारी एजेंसियों के लिए डेटा एन्क्रिप्शन मानक के रूप में अपनाया गया। हाल ही में प्रशंसित राष्ट्रीय सुरक्षा एजेंसी दस्तावेजों को संग्रहीत करने के लिए इसका उपयोग करती है: SECRET स्तर तक, 128 बिट्स की कुंजी के साथ एन्क्रिप्शन का उपयोग किया जाता है, TOP SECRET जानकारी के लिए 192 या 256 बिट्स की कुंजी की आवश्यकता होती है। उच्च क्रिप्टोग्राफिक ताकत के अलावा, एल्गोरिथ्म सबसे जटिल गणित पर आधारित नहीं है।

ढेर सारा एन्क्रिप्शन

काम करने के लिए, हमें एन्क्रिप्शन ऑब्जेक्ट के रूप में बाइट्स के एक सेट और डिक्रिप्शन के दौरान एक गुप्त कुंजी की आवश्यकता होगी। आपके सिर में लंबे समय तक चाबियाँ रखना असुविधाजनक है, और यह माना जाता है कि कुंजी की लंबाई 128 बिट्स है, दुर्गमता के लिए पर्याप्त से अधिक है, इसलिए मैंने विकल्प 192/256 को नहीं देखा। इसके अलावा, जैसा कि यहां कहा गया है , कुछ शर्तों के तहत, एक लंबी कुंजी स्थिरता में पिछड़ सकती है।

हम कुछ संकेतन प्रस्तुत करते हैं:

राज्य एन्क्रिप्शन का एक मध्यवर्ती परिणाम है, जिसे 4 पंक्तियों और एनबी कॉलम के साथ बाइट्स के आयताकार सरणी के रूप में दर्शाया जा सकता है। प्रत्येक राज्य सेल में 1 बाइट का मान होता है
Nb उन कॉलमों की संख्या (32-बिट शब्द) है जो स्टेट बनाते हैं। मानक Nb = 4 के लिए विनियमित
32-बिट शब्दों में एनके प्रमुख लंबाई है। एईएस के लिए, एनके = 4, 6, 8. हमने पहले ही तय कर लिया है कि हम एनके = 4 का उपयोग करेंगे
एनआर - एन्क्रिप्शन के दौर की संख्या। प्रमुख लंबाई के आधार पर, Nr = 10, 12 या 14

एल्गोरिथ्म में चार परिवर्तन होते हैं, जिनमें से प्रत्येक अपने तरीके से राज्य की स्थिति को प्रभावित करता है और अंततः परिणाम की ओर जाता है: सबबाइट्स (), ShiftRows (), मिक्सकॉलीमेंट्स () और AddRoundKey () । सामान्य एन्क्रिप्शन योजना के रूप में प्रतिनिधित्व किया जा सकता है:

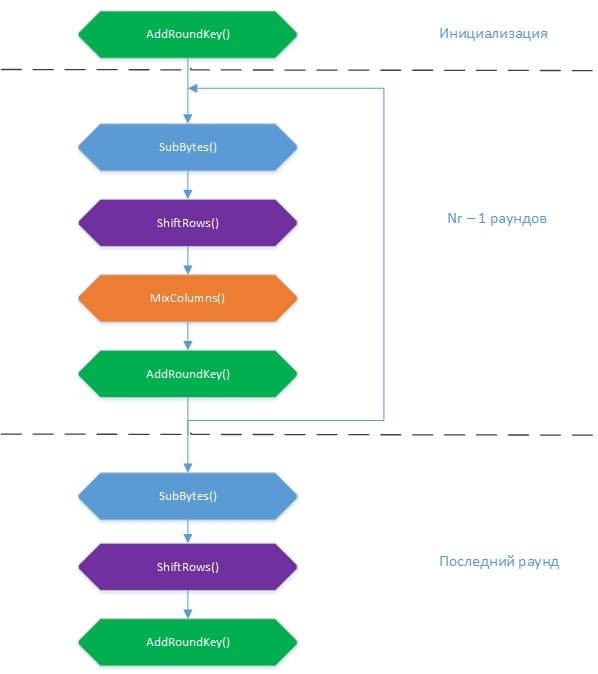
शुरुआत में, राज्य सरणी सूत्र के अनुसार इनपुट मान से भर जाती है राज्य [r] [c] = इनपुट [r + 4c], r = 0.1 ... 4; c = 0.1..Nb । वह है, कॉलम में। एक बार में 16-बाइट ब्लॉक एन्क्रिप्ट किया गया है।

एल्गोरिथ्म बाइट्स के साथ संचालित होता है, उन्हें एक परिमित क्षेत्र या गैलोज़ फील्ड जीएफ (2 ⁸ ) के तत्व मानते हैं। कोष्ठक में संख्या क्षेत्र तत्वों या उसकी शक्ति की संख्या है। फ़ील्ड GF (2 ⁸ ) के तत्व अधिकांश 7 पर डिग्री के बहुपद हैं, जिन्हें उनके गुणांकों की एक पंक्ति द्वारा निर्दिष्ट किया जा सकता है। बहुपद के रूप में बाइट का प्रतिनिधित्व करना बहुत आसान है। उदाहरण के लिए, बाइट {1,1,1,0,0,1,1,1} एक फ़ील्ड तत्व 1x ⁷ + 1x ⁶ + 1x ⁵ + 0x ⁴ + 0x ³ + 0x ² + 1x ¹ + 1x ⁰ + 1x ⁷ + से मेल खाती है 1x ⁶ + 1x ⁵ + x +1। यह तथ्य कि हम फील्ड तत्वों के साथ काम करते हैं, बहुत महत्वपूर्ण है क्योंकि यह जोड़ और गुणा संचालन के नियमों को बदलता है। हम थोड़ी देर बाद इस पर विचार करेंगे।

अगला, हम प्रत्येक परिवर्तन के बारे में विस्तार से विचार करते हैं।

SybButes ()

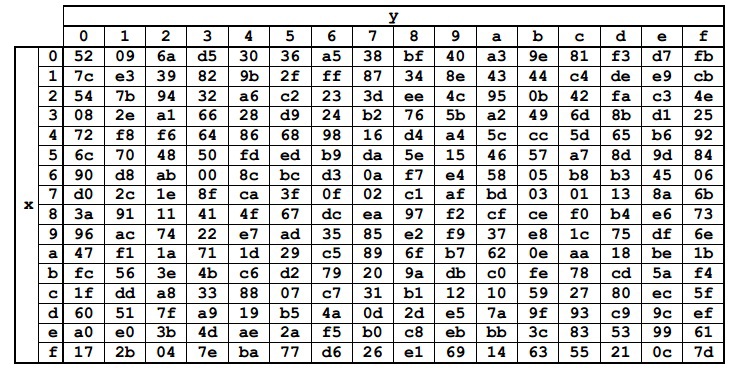
एक रूपांतरण Sbox स्थिर तालिका से संबंधित एक के साथ राज्य से प्रत्येक बाइट का प्रतिस्थापन है। हेक्साडेसिमल नोटेशन में Sbox तत्व मानों का प्रतिनिधित्व किया जाता है। हमारे द्वारा पहले से ज्ञात फ़ील्ड GF (2 ⁸ ) को रूपांतरित करके तालिका स्वयं प्राप्त की गई थी

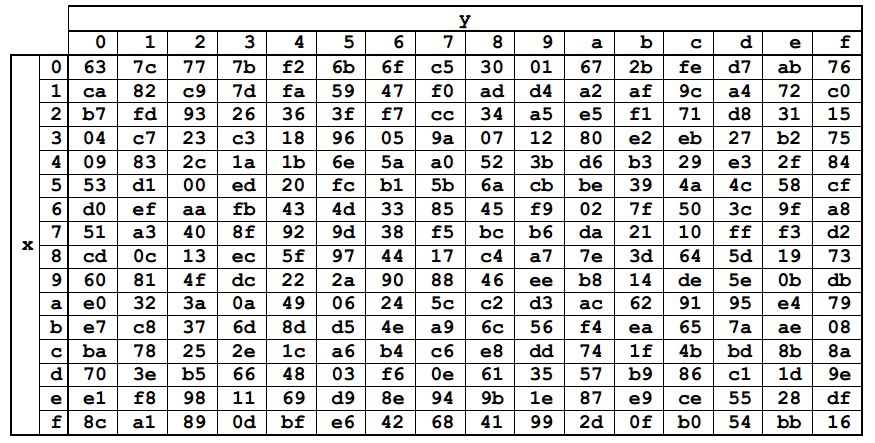
राज्य से प्रत्येक बाइट को हेक्साडेसिमल नोटेशन में {xy} के रूप में दर्शाया जा सकता है। फिर आपको इसे पंक्ति x और कॉलम y के चौराहे पर एक तत्व के साथ बदलना चाहिए। उदाहरण के लिए, {6e} को {9f}, और {15} को {59} से बदल दिया जाएगा।

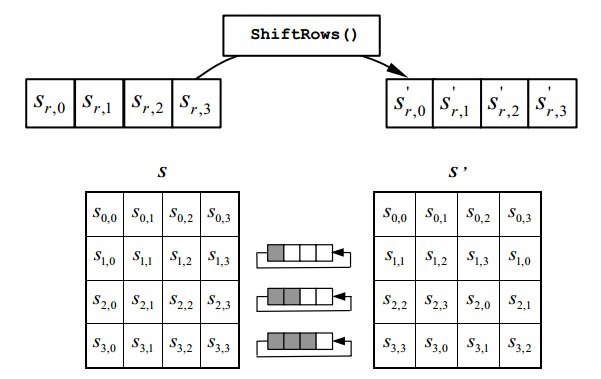
ShiftRows ()

सरल परिवर्तन। यह पहली पंक्ति के लिए 1 तत्व, दूसरी के लिए 2 और तीसरे के लिए 3 द्वारा एक चक्रीय छोड़ दिया पारी करता है। शून्य रेखा को स्थानांतरित नहीं किया गया है।

मिक्सकॉल्यूमन्स ()

इस परिवर्तन के हिस्से के रूप में, स्टेट के प्रत्येक कॉलम को एक बहुपद के रूप में दर्शाया गया है और GF (2 ⁸ ) फ़ील्ड modulo x ⁴ + 1 में गुणा किया गया है, एक निश्चित बहुपद 3x ³ + x ² + x + 2. के साथ यह सरल लगता है, लेकिन यह कैसे करना है यह स्पष्ट नहीं है। । यदि आप मानक के आधिकारिक दस्तावेज में दी गई समकक्ष मैट्रिक्स प्रविष्टि को देखते हैं तो चित्र सरल हो जाता है:

मैट्रिसेस को गुणा करते समय, _{Ij का} मान पहले मैट्रिक्स के i-th रो के संगत तत्वों और दूसरे के j-th कॉलम के योग के रूप में प्राप्त किया जाता है, अर्थात।

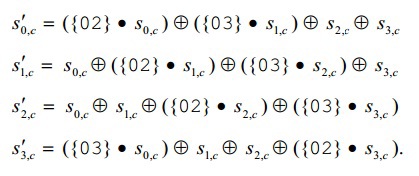
यहां हमें जोड़ और गुणा के सामान्य नियमों की अक्षमता को याद करने की आवश्यकता है।
नए नियम:

जीएफ (2 ⁸ ) क्षेत्र में जोड़ ऑपरेशन एक्सओआर के बराबर है
{01} से गुणा करने से गुणन नहीं बदलता है
{02} गुणा गुणा नियम के अनुसार किया जाता है: यदि गुणा मान {80} से कम है, तो इसे 1 बिट से बाईं ओर स्थानांतरित किया जाता है। यदि गुणा मान {80} से अधिक या उसके बराबर है, तो इसे पहले 1 बिट द्वारा छोड़ दिया जाता है, और फिर मान {1b} के साथ XOR ऑपरेशन को शिफ्ट के परिणाम पर लागू किया जाता है। परिणाम मान {ff} को छोड़ सकता है, अर्थात, एक बाइट की सीमाओं से परे। इस मामले में, आपको परिणाम को {100} से विभाजित करने से शेष को वापस करने की आवश्यकता है।
अन्य स्थिरांक द्वारा गुणा पिछले के माध्यम से व्यक्त किया जा सकता है

स्वाभाविक रूप से, ये अंतिम क्षेत्र में अंकगणित के सामान्य नियम नहीं हैं, लेकिन एल्गोरिथ्म के भाग के रूप में, आपको एन्क्रिप्शन के लिए तीन स्थिरांक और डिक्रिप्शन के लिए चार गुणा करना होगा, इसलिए ऐसे स्थानीय जीवन हैक पर्याप्त होंगे।
MixRolumns () ShiftRows () के साथ सिफर में प्रसार जोड़ें।

AddRoundKey ()

परिवर्तन RoundKey से संबंधित तत्व के साथ राज्य से प्रत्येक तत्व का एक बिटवेअर XOR उत्पन्न करता है। RoundKey स्टेट के समान आकार का एक सरणी है, जिसे KeyExpansion () फ़ंक्शन के साथ गुप्त कुंजी के आधार पर प्रत्येक दौर के लिए बनाया गया है, जिसे हम बाद में विचार करेंगे।

KeyExpansion ()

यह सहायक परिवर्तन गोल कुंजी का एक समूह बनाता है - KeySchedule। KeySchedule Nb * (Nr + 1) कॉलम या (Nr + 1) ब्लॉक से मिलकर एक लंबी तालिका है, जिनमें से प्रत्येक राज्य के आकार के बराबर है। सूत्र के अनुसार, आप जिस गुप्त कुंजी के साथ आते हैं, उसके आधार पर पहले राउंड की को भरा जाता है
KeySchedule [r] [c] = SecretKey [r + 4c], r = 0.1 ... 4; c = 0,1..Nk।

यह स्पष्ट है कि KeySchedule में हमें बाइट दर्ज करनी चाहिए ताकि आगे संचालन संभव हो। यदि आप इस एन्क्रिप्शन का उपयोग होम एन्क्रिप्शन के लिए करते हैं, तो यह आपके सिर में संख्याओं के अनुक्रम को संग्रहीत करने के लिए बिल्कुल भी सुविधाजनक नहीं है, इसलिए हमारे कार्यान्वयन में KeyExpansion () प्रत्येक वर्ण के लिए एक सादा इनपुट लेगा और ord() उपयोग करेगा, परिणाम Key Keychedule कोशिकाओं में लिखें। इसका मतलब यह है कि सीमाएँ: 16 से अधिक वर्णों की लंबाई और, जब से हम बाइट्स के साथ काम करते हैं, तो ord() वर्ण के ord() बाइनरी में 255 या 11111111 से अधिक मान नहीं लौटाने चाहिए, अन्यथा हम आउटपुट पर गलत एन्क्रिप्शन प्राप्त करेंगे। यह पता चला है कि रूसी में एक कुंजी की मदद से, एन्क्रिप्शन काम नहीं करेगा।

यह आंकड़ा एईएस -128: 4 कॉलम के 11 ब्लॉकों के लिए कीस्कुलेड लेआउट दिखाता है। एल्गोरिथ्म के अन्य रूपों के लिए, क्रमशः Nb कॉलम के (Nr + 1) ब्लॉक होंगे। अब हमें खाली जगहों को भरना होगा। रूपांतरणों के लिए, एक निरंतर तालिका को फिर से परिभाषित किया गया है - Rcon - जिसका मान हेक्साडेसिमल संख्या प्रणाली में है।

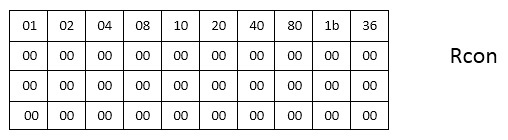
KeySchedule रीफिल एल्गोरिथ्म:

प्रत्येक पुनरावृत्ति पर, हम एक तालिका स्तंभ के साथ काम करते हैं। कॉलम 0, .., (Nk - 1) पहले से ही गुप्त शब्द के मानों से पहले से आबाद है। हम स्तंभ संख्या Nk से शुरू करते हैं (हमारे मामले में, चौथे के साथ)
यदि कॉलम संख्या W _i , Nk (हमारे मामले में, हर चौथे) में एक बहु है, तो हम कॉलम W _i-1 को लेते हैं, एक तत्व द्वारा बाईं ओर एक चक्रीय पारी करते हैं, फिर कॉलम के सभी बाइट्स को Sbox तालिका से संबंधित लोगों के साथ बदलें, जैसा कि उन्होंने उप-बाइट्स () में किया था। । अगला, स्तंभ W _i-Nk , संशोधित W _i-1 और कॉलम Rcon _{i / Nk-1 के} बीच XOR ऑपरेशन करें। परिणाम कॉलम W _i को लिखा जाता है। इसे थोड़ा और स्पष्ट करने के लिए, i = 4 के लिए चित्रण।
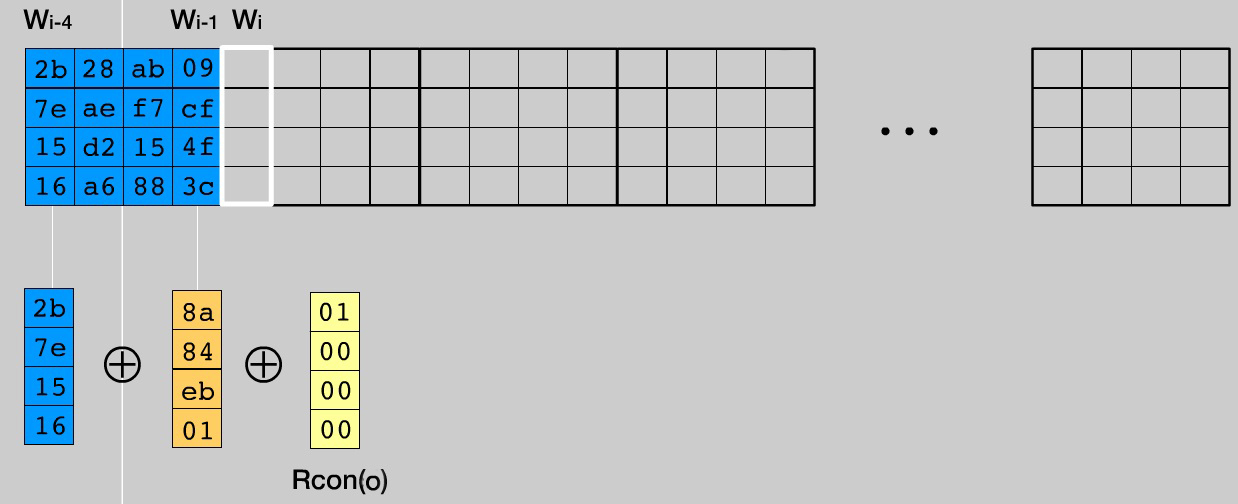
शेष कॉलमों के लिए, W _i-Nk और W _{i-1 के} बीच XOR करें। परिणाम डब्ल्यू _i में लिखा गया है

एल्गोरिथ्म में मिक्सकॉल्यूमिनेशन () में गणित की मान्यता के बाद, यह सहायक परिवर्तन लेखन में सबसे अधिक चमकदार है और, शायद, सबसे जटिल है। एक क्रिप्टोग्राफिक कुंजी में 4 * एनके तत्व शामिल होने चाहिए (हमारे मामले में 16)। लेकिन जब से हम यह सब घरेलू उपयोग के लिए कर रहे हैं, यह संभावना है कि हर कोई 16-चरित्र की कुंजी के साथ नहीं आएगा और इसे याद रखेगा। इसलिए, यदि इनपुट पर 16 से कम की लंबाई वाली एक पंक्ति, मैं KeySchedule में मान {01} को आदर्श में जोड़ देगा।

KeyExpansion () कोड

 def key_expansion(key): key_symbols = [ord(symbol) for symbol in key] # ChipherKey shoul contain 16 symbols to fill 4*Nk table. If it's less # complement the key with "0x01" if len(key_symbols) < 4*nk: for i in range(4*nk - len(key_symbols)): key_symbols.append(0x01) # make ChipherKey(which is base of KeySchedule) key_schedule = [[] for i in range(4)] for r in range(4): for c in range(nk): key_schedule[r].append(key_symbols[r + 4*c]) # Comtinue to fill KeySchedule for col in range(nk, nb*(nr + 1)): # col - column number if col % nk == 0: # take shifted (col - 1)th column... tmp = [key_schedule[row][col-1] for row in range(1, 4)] tmp.append(key_schedule[0][col-1]) # change its elements using Sbox-table like in SubBytes... for j in range(len(tmp)): sbox_row = tmp[j] // 0x10 sbox_col = tmp[j] % 0x10 sbox_elem = sbox[16*sbox_row + sbox_col] tmp[j] = sbox_elem # and finally make XOR of 3 columns for row in range(4): s = key_schedule[row][col - 4]^tmp[row]^rcon[row][col/nk - 1] key_schedule[row].append(s) else: # just make XOR of 2 columns for row in range(4): s = key_schedule[row][col - 4]^key_schedule[row][col - 1] key_schedule[row].append(s) return key_schedule

जैसा कि पहले कहा गया है, AddSoundKey () के परिवर्तन में KeySchedule का उपयोग किया जाता है। शुरुआती दौर में, गोल कुंजी संख्या 0, .., 3 के साथ कॉलम होगी, पहले में - संख्या 4, .., 7, आदि के साथ। AddRoundKey () का संपूर्ण बिंदु एक XOR स्टेट और एक गोल कुंजी का उत्पादन करना है।

यह, वास्तव में, सभी एन्क्रिप्शन प्रक्रिया के बारे में है। एन्क्रिप्टेड बाइट्स का आउटपुट सरणी फॉर्मूला आउटपुट [r + 4c] = स्टेट [r] [c], r = 0.1 ... 4 के अनुसार स्टेट से संकलित किया जाता है ; c = 0.1..Nb । इस बीच, लेख में देरी हो रही है, इसलिए अब हम जल्दी से डिक्रिप्शन प्रक्रिया से गुजरेंगे।

डिक्रिप्शन के बारे में जल्दी

यहां विचार सरल है: यदि आप उन परिवर्तनों के अनुक्रम को निष्पादित करते हैं जो एक ही कीवर्ड के साथ एन्क्रिप्शन परिवर्तनों के विपरीत हैं, तो आपको मूल संदेश मिलता है। ऐसे प्रतिलोम परिवर्तन InvSubBytes (), InvShiftRows (), InvMixColumns (), और AddRoundKey () हैं । डिक्रिप्शन एल्गोरिथ्म की सामान्य योजना:

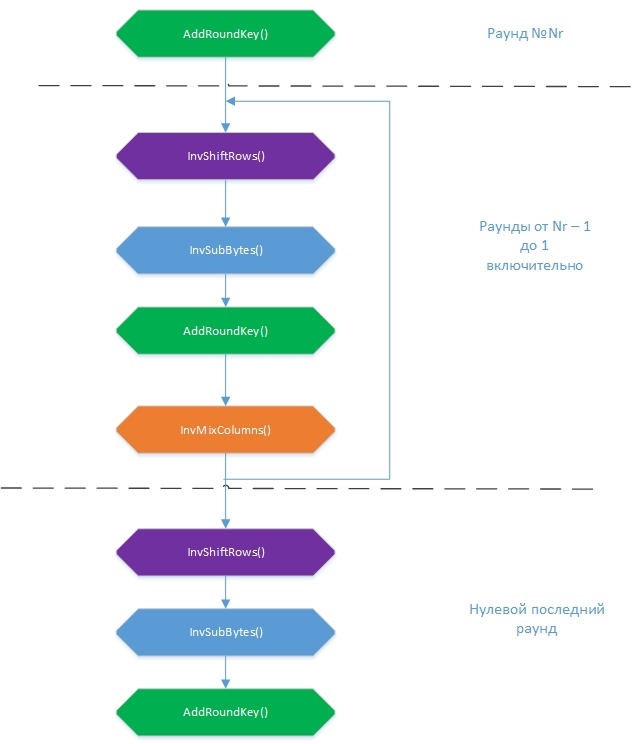
यह ध्यान दिया जाना चाहिए कि AddRoundKey () के लिए गोल कुंजी जोड़ने का क्रम रिवर्स होना चाहिए: Nr + 1 से 0. प्रारंभ में, एन्क्रिप्शन के साथ, स्टेट टेबल इनपुट बाइट्स के सरणी से बनता है। फिर, इसके ऊपर, प्रत्येक दौर में, रूपांतरण किए जाते हैं, जिसके अंत में एक डिक्रिप्टेड फ़ाइल प्राप्त की जानी चाहिए। परिवर्तनों का क्रम थोड़ा बदल गया है। सबसे पहले क्या होगा, इनवसबाइट्स () या इनवाइटफ्राइट्स (), वास्तव में महत्वपूर्ण नहीं है, क्योंकि उनमें से एक बाइट मूल्यों के साथ काम करता है, और दूसरा इन मूल्यों को बदलने के बिना, बाइट्स को फिर से व्यवस्थित करता है, लेकिन मानक छद्मकोश में रूपांतरण के अनुक्रम का पालन करता है।

InvSubBytes ()

यह बिल्कुल SubBytes () के समान काम करता है, सिवाय इसके कि InvSbox निरंतर तालिका से प्रतिस्थापन किए जाते हैं।

शेष रिवर्स ट्रांसफॉर्मेशन भी उनके प्रत्यक्ष समकक्षों के समान होगा, इसलिए कोड में हम उनके लिए अलग-अलग फ़ंक्शन का चयन नहीं करते हैं। प्रत्येक फ़ंक्शन जो परिवर्तन का वर्णन करता है, उसमें एक परिवर्तनशील चर होगा। यदि यह False , तो फ़ंक्शन सामान्य या प्रत्यक्ष मोड (एन्क्रिप्शन) में काम करेगा, यदि True - उलटा मोड (डिक्रिप्शन) में।

कोड

 def sub_bytes(state, inv=False): if inv == False: # encrypt box = sbox else: # decrypt box = inv_sbox for i in range(len(state)): for j in range(len(state[i])): row = state[i][j] // 0x10 col = state[i][j] % 0x10 # Our Sbox is a flat array, not a bable. So, we use this trich to find elem: box_elem = box[16*row + col] state[i][j] = box_elem return state

InvShiftRows ()

राज्य के पहले पंक्ति के लिए 1 तत्व द्वारा दाईं ओर परिवर्तन चक्र, दूसरे के लिए 2 और तीसरे के लिए 3। शून्य रेखा घूमती नहीं है।

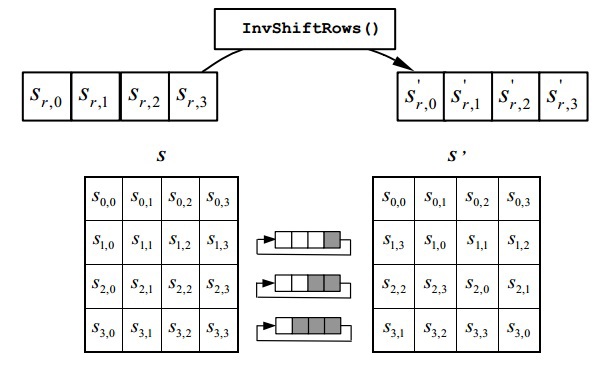
कोड के लिए स्पष्टीकरण: left_shift/right_shift(array, count) इनपुट array को संबंधित दिशा में left_shift/right_shift(array, count) घुमाएं

कोड

 def shift_rows(state, inv=False): count = 1 if inv == False: # encrypting for i in range(1, nb): state[i] = left_shift(state[i], count) count += 1 else: # decryption for i in range(1, nb): state[i] = right_shift(state[i], count) count += 1 return state

InvMixColumns ()

संचालन समान हैं, लेकिन प्रत्येक राज्य स्तंभ एक अलग बहुपद {0b} x ³ + {0d} x ² + {09} x + {0e} से गुणा किया जाता है। मैट्रिक्स के रूप में, यह इस तरह दिखता है:

या तैयार किए गए सूत्र। सभी मूल्य, निश्चित रूप से, हेक्साडेसिमल संकेतन में हैं।

यहां आपको गणित की ओर खुदाई करने की आवश्यकता है और बताएं कि {02} से अधिक स्थिरांक द्वारा गुणा करने के कार्य कैसे प्राप्त करें। जैसा कि मैंने कहा, वे इन्हें {01} और {02} के माध्यम से विघटित करके प्राप्त करते हैं, अर्थात्:

रूपांतरण

n * {03} = n * ({02} + {01}) = n * {02} + n * {01}
n * {09} = n * ({08} + {01}) = n * {02} * {02} * {02} + n * {01}
n * {0b} = n * ({08} + {02} + {01}) = b * {02} * {02} * {02} + n * {02} + n * {01}
n * {0d} = n * ({08} + {04} + {01}) = n * {08} + n * {04} + n * {01} = n * {02} * {02} * {02} + n * {02} * {02} + n * {01}
n * {0} = n * ({08} + {04} + {02} = n * {08} + n * {04} + n * {02} = n * {02} * {02} * { 02} + n * {02} * {02} + b * {02}

बेशक, एक संख्या को दूसरे तरीके से विघटित किया जा सकता है, लेकिन यह व्यक्तिगत रूप से सत्यापित किया जाता है कि अपघटन
n * {09} = n * {03} + n * {03} + n * {03}
और संबंधित कार्यों को कॉल करने से गलत परिणाम मिलेगा (संदर्भ तालिका स्रोत सूची में लिंक में से एक में हैं)। उन्होंने गणनाओं के विशेष रूप से वैकल्पिक (टिप्पणी) संस्करणों को छोड़ दिया, क्योंकि वे अधिक समझने योग्य, सुरुचिपूर्ण हैं, लेकिन किसी कारण से वे गलत तरीके से काम करते हैं।

सहायक गुणन कार्य

 def mul_by_02(num): if num < 0x80: res = (num << 1) else: res = (num << 1)^0x1b return res % 0x100 def mul_by_03(num): return mul_by_02(num)^num def mul_by_09(num): #return mul_by_03(num)^mul_by_03(num)^mul_by_03(num) - works wrong, I don't know why return mul_by_02(mul_by_02(mul_by_02(num)))^num def mul_by_0b(num): #return mul_by_09(num)^mul_by_02(num) return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(num)^num def mul_by_0d(num): #return mul_by_0b(num)^mul_by_02(num) return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(mul_by_02(num))^num def mul_by_0e(num): #return mul_by_0d(num)^num return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(mul_by_02(num))^mul_by_02(num)

कोड के लिए स्पष्टीकरण: फ़ंक्शन mul_by_<> GF (2 ⁸ ) में संगत mul_by_<> द्वारा गुणा किया जाता है, जो मिक्सकॉल्यूमन्स () के बारे में अनुभाग में वर्णित नियमों के अनुसार था।

कोड

  def mix_columns(state, inv=False): for i in range(nb): if inv == False: # encryption s0 = mul_by_02(state[0][i])^mul_by_03(state[1][i])^state[2][i]^state[3][i] s1 = state[0][i]^mul_by_02(state[1][i])^mul_by_03(state[2][i])^state[3][i] s2 = state[0][i]^state[1][i]^mul_by_02(state[2][i])^mul_by_03(state[3][i]) s3 = mul_by_03(state[0][i])^state[1][i]^state[2][i]^mul_by_02(state[3][i]) else: # decryption s0 = mul_by_0e(state[0][i])^mul_by_0b(state[1][i])^mul_by_0d(state[2][i])^mul_by_09(state[3][i]) s1 = mul_by_09(state[0][i])^mul_by_0e(state[1][i])^mul_by_0b(state[2][i])^mul_by_0d(state[3][i]) s2 = mul_by_0d(state[0][i])^mul_by_09(state[1][i])^mul_by_0e(state[2][i])^mul_by_0b(state[3][i]) s3 = mul_by_0b(state[0][i])^mul_by_0d(state[1][i])^mul_by_09(state[2][i])^mul_by_0e(state[3][i]) state[0][i] = s0 state[1][i] = s1 state[2][i] = s2 state[3][i] = s3 return state

AddRoundKey ()

एक्सओआर ऑपरेशन की संपत्ति के कारण यह परिवर्तन अपने आप में उलटा है:

(एक एक्सओआर बी) एक्सओआर बी = ए

इसलिए, इसमें कोई बदलाव करने की जरूरत नहीं है। गोल कुंजियों का एक सेट उसी तरह बनता है जैसे एन्क्रिप्शन के लिए KeyExpansion () फ़ंक्शन का उपयोग करते हैं, लेकिन रिवर्स ऑर्डर में गोल कुंजी को प्रतिस्थापित किया जाना चाहिए।

कोड

 def add_round_key(state, key_schedule, round=0): for col in range(nk): # nb*round is a shift which indicates start of a part of the KeySchedule s0 = state[0][col]^key_schedule[0][nb*round + col] s1 = state[1][col]^key_schedule[1][nb*round + col] s2 = state[2][col]^key_schedule[2][nb*round + col] s3 = state[3][col]^key_schedule[3][nb*round + col] state[0][col] = s0 state[1][col] = s1 state[2][col] = s2 state[3][col] = s3 return state

अब हमारे पास लिखने के लिए सहायक परिवर्तन कार्यों का एक व्यापक सेट है

एन्क्रिप्शन फ़ंक्शन

 def encrypt(input_bytes, key): # let's prepare our input data: State array and KeySchedule state = [[] for j in range(4)] for r in range(4): for c in range(nb): state[r].append(input_bytes[r + 4*c]) key_schedule = key_expansion(key) state = add_round_key(state, key_schedule) for rnd in range(1, nr): state = sub_bytes(state) state = shift_rows(state) state = mix_columns(state) state = add_round_key(state, key_schedule, rnd) state = sub_bytes(state) state = shift_rows(state) state = add_round_key(state, key_schedule, rnd + 1) output = [None for i in range(4*nb)] for r in range(4): for c in range(nb): output[r + 4*c] = state[r][c] return output

डिक्रिप्शन फ़ंक्शन

 def decrypt(cipher, key): # let's prepare our algorithm enter data: State array and KeySchedule state = [[] for i in range(nb)] for r in range(4): for c in range(nb): state[r].append(cipher[r + 4*c]) key_schedule = key_expansion(key) state = add_round_key(state, key_schedule, nr) rnd = nr - 1 while rnd >= 1: state = shift_rows(state, inv=True) state = sub_bytes(state, inv=True) state = add_round_key(state, key_schedule, rnd) state = mix_columns(state, inv=True) rnd -= 1 state = shift_rows(state, inv=True) state = sub_bytes(state, inv=True) state = add_round_key(state, key_schedule, rnd) output = [None for i in range(4*nb)] for r in range(4): for c in range(nb): output[r + 4*c] = state[r][c] return output

ये दो फ़ंक्शन बाइट्स की एक सूची लेते हैं जो एन्क्रिप्ट या एन्क्रिप्टेड नहीं हैं, और एक गुप्त कीवर्ड के साथ एक प्लेनटेक्स्ट स्ट्रिंग।

निष्कर्ष, दिलचस्प लिंक

लेख काफी लंबा निकला। मैंने चित्रों के साथ पाठ को पतला करने की कोशिश की और मुझे उम्मीद है, यह आपके लिए दिलचस्प था और कोई भी ऊब नहीं था। लेख में प्रस्तुत कोड पूरी तरह से समाप्त नहीं हुआ है। मैंने लगातार तालिकाओं की वैश्विक घोषणा नहीं की, मिक्सकॉल्यूमन्स () के लिए छोटे कार्य, लेकिन केवल शब्दों में मैंने समझाया कि वे कहीं हैं। यह मत समझो कि मैं पीआर हूं, लेकिन पूर्ण, सरेस से जोड़ा हुआ कोड एक रिपॉजिटरी में लिया जा सकता है । एक मामूली सीएलआई इंटरफ़ेस भी है जो आपको बस फ़ाइल को पथ निर्दिष्ट करने की अनुमति देता है, गुप्त कुंजी दर्ज करें और स्रोत के रूप में उसी निर्देशिका में एन्क्रिप्टेड फ़ाइल प्राप्त करें (डिक्रिप्ट की गई फ़ाइल उसी तरह प्राप्त की जा सकती है)। स्वास्थ्य के लिए एन्क्रिप्ट!

और अंत में एक महत्वपूर्ण बारीकियों के बारे में कहना आवश्यक है - ब्लॉक के लिए पैडिंग या इसके अलावा। एईएस एक ब्लॉक एन्क्रिप्शन एल्गोरिथ्म है, encrypt()/decrypt() फ़ंक्शन इनपुट बाइट्स के बिल्कुल एक ब्लॉक लेते हैं (128-बिट कुंजी के साथ हमारे संस्करण के लिए, यह 16 बाइट्स है)। फ़ाइल के अंत में, 1 से 15 बाइट्स रह सकते हैं जो एक भी ब्लॉक नहीं बनाते हैं। आप बस उन्हें एन्क्रिप्शन के बिना गंतव्य फ़ाइल पर भेज सकते हैं, लेकिन कुछ मामलों में, फ़ाइल के अंत में, कुछ महत्वपूर्ण निहित हो सकता है, और यह विकल्प उपयुक्त नहीं है। दूसरा विकल्प मुझे विकिपीडिया लेख द्वारा ब्लॉक सिफर के बारे में सुझाया गया था

शून्य बिट का एक साधारण जोड़ समस्या का समाधान नहीं करता है, क्योंकि प्राप्तकर्ता पेलोड का अंत नहीं पा सकता है। इसके अलावा, यह विकल्प Oracle ऐड-ऑन द्वारा हमलों की ओर जाता है। इसलिए, व्यवहार में, आईएसओ / IEC 9797-1 में "अतिरिक्त विधि 2" के रूप में मानकीकृत समाधान लागू है, संदेश के अंत में एक सा जोड़कर और शेष स्थान को शून्य के साथ भरना है। इस मामले में, ऐसे हमलों का प्रतिरोध साबित हुआ था।

तो मैंने किया (हालांकि पहला विकल्प बना रहा, सिर्फ टिप्पणी की। अचानक, और काम में आना)।

स्रोत चयन:

आधिकारिक दस्तावेज
एल्गोरिथ्म के एन्क्रिप्शन भाग की बहुत स्पष्ट दृश्य व्याख्या । लेखक ने मुझ पर मुकदमा नहीं किया, मैंने वहां से कुछ स्क्रीनशॉट लिए।
विकीपीडिया के बिना कहीं नहीं
MixColumns () के बारे में एक अलग लेख । इसमें 0 की संख्या को गुणा करने के परिणामों के साथ तालिकाएँ शामिल हैं ... GF फ़ील्ड (2) में सिफर में प्रयुक्त स्थिरांक द्वारा 255
एईएस के इतिहास और खुद एल्गोरिथ्म के बारे में मजेदार हास्य । यह अफ़सोस की बात है कि मुझे यह तभी मिला जब मैं पहले से ही एक लेख लिख रहा था।

एईएस 128। अजगर में विवरण और कार्यान्वयन

थोड़ा सा परिचय

ढेर सारा एन्क्रिप्शन

SybButes ()

ShiftRows ()

मिक्सकॉल्यूमन्स ()

AddRoundKey ()

KeyExpansion ()

डिक्रिप्शन के बारे में जल्दी

InvSubBytes ()

InvShiftRows ()

InvMixColumns ()

AddRoundKey ()

निष्कर्ष, दिलचस्प लिंक

More articles: