
शुभ दिन, पाठक।
रैंडम फ़ॉरेस्ट आज मशीन सीखने की समस्याओं को हल करने के लिए सबसे लोकप्रिय और बेहद प्रभावी तरीकों में से एक है, जैसे कि वर्गीकरण और प्रतिगमन। दक्षता के संदर्भ में, यह संदर्भ वेक्टर मशीनों, तंत्रिका नेटवर्क और बूस्टिंग के साथ प्रतिस्पर्धा करता है, हालांकि यह निश्चित रूप से इसकी कमियों के बिना नहीं है। उपस्थिति में, लर्निंग अल्गोरिदम अत्यंत सरल है (तुलना में, कहते हैं, सपोर्ट वैक्टर की लर्निंग मशीन अल्गोरिदम, जिनके जीवन में थ्रिल बहुत कम है, मैं आपके अवकाश के समय ऐसा करने की सलाह देता हूं)। हम रैंडम फ़ॉरेस्ट (बाइनरी निर्णय ट्री, बूटस्ट्रैप एकत्रीकरण या बैगिंग, रैंडम सबस्पेस विधि और सजावट) में निहित मुख्य विचारों को एक सुलभ रूप में समझने की कोशिश करेंगे और समझेंगे कि यह सब एक साथ क्यों काम करता है। अपने प्रतिद्वंद्वियों के संबंध में मॉडल अभी भी काफी युवा है: यह सब
1997 के एक
लेख के साथ शुरू हुआ, जिसमें लेखकों ने नए पेड़ के नोड्स बनाते समय विशेषताओं के यादृच्छिक उप-स्थान का उपयोग करके एकल निर्णय पेड़ के निर्माण के लिए एक विधि का प्रस्ताव दिया; तब लेखों की एक श्रृंखला थी, जिसका समापन
2001 में एल्गोरिथ्म के एक विहित संस्करण के प्रकाशन में हुआ, जिसमें बूटस्ट्रैप एकत्रीकरण, या बैगिंग के आधार पर निर्णय पेड़ों का एक समूह बनाया गया है। अंत में, हम इस मॉडल को c # में लागू करने के लिए एक सरल, बिल्कुल दृश्य नहीं, बल्कि बेहद दृश्य तरीका देंगे, साथ ही परीक्षणों की एक श्रृंखला भी। वैसे,
दाईं ओर की
तस्वीर में आप एक वास्तविक यादृच्छिक जंगल देख सकते हैं जो
क्यूरोनियन स्पिट पर कलिनिनग्राद क्षेत्र में बढ़ता है।
बाइनरी निर्णय पेड़
आपको पेड़ से शुरू करना चाहिए, जैसे कि जंगल के मुख्य संरचनात्मक तत्व के साथ, लेकिन अध्ययन के तहत मॉडल के संदर्भ में। प्रस्तुति इस धारणा पर आधारित होगी कि पाठक समझता है कि
डेटा संरचना के रूप में एक पेड़ कैसा है । पेड़ का निर्माण
लगभग कार्ट (वर्गीकरण और प्रतिगमन वृक्ष)
एल्गोरिथ्म के अनुसार किया
जाएगा , जो द्विआधारी निर्णय पेड़ों का निर्माण करता है। वैसे, यहां हब
पर एंट्रॉपी को कम करने के आधार पर ऐसे
पेड़ों के निर्माण पर एक उपयुक्त लेख है, हमारे संस्करण में यह एक विशेष मामला होगा। इसलिए संकेतों की एक जगह की कल्पना करें, दो आयामी बोलें, ताकि कल्पना करना आसान हो, जिसमें दो वर्गों के कई ऑब्जेक्ट दिए गए हैं।

हम कई संकेतन पेश करते हैं। हम सुविधाओं के सेट को निम्नानुसार दर्शाते हैं:
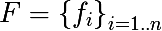
प्रत्येक सुविधा के लिए, कोई भी प्रशिक्षण सेट के आधार पर, या समस्या के बारे में अन्य प्राथमिक जानकारी का उपयोग करके अपने मूल्यों के सेट को अलग कर सकता है, हम विशेषता के मूल्यों के परिमित सेट का अनुसरण करते हैं:
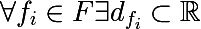
इसके लेबल के संबंध
में एक सेट की
विविधता के तथाकथित माप को पेश करना भी आवश्यक है। कल्पना करें कि प्रशिक्षण सेट के एक निश्चित सबसेट में
5 लाल और
10 नीली वस्तुएं होती हैं, तो हम कह सकते हैं कि इस सबसेट में लाल वस्तु को खींचने की संभावना
1/3 और नीले
2/3 होगी । आइए हम निरूपित करें कि प्रशिक्षण सेट के कुछ सबसेट में kth वर्ग की संभावना निम्नानुसार है:
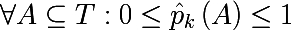
इस प्रकार, हमने टिप्पणियों के एक सबसेट में लेबल के एक अनुभवजन्य असतत संभाव्य वितरण को परिभाषित किया। इस उपसमुच्चय की
विषमता के माप को निम्नलिखित रूप का कार्य कहा जाएगा, जहाँ
K (A) उपसमूह
A के कुल लेबल है:
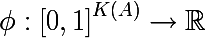
विषमता का माप इस तरह से निर्धारित किया जाता है कि फ़ंक्शन का मान सेट
की बढ़ती
विविधता के साथ जितना संभव हो उतना बढ़ जाता है, जब अधिकतम सेट में सभी प्रकार के लेबल होते हैं, और न्यूनतम यदि सेट में केवल एक ही वर्ग के लेबल होते हैं (मैं आपको देखने की सलाह देता हूं
। चित्रों के साथ एन्ट्रापी उदाहरण )।
आइए विषमता के कुछ उदाहरणों पर एक नज़र डालें (वेक्टर
पी में प्रशिक्षण सेट के कुछ सबसेट
ए में पाए गए लेबल की
मी संभाव्यताएं शामिल हैं):
द्विआधारी निर्णय वृक्ष के निर्माण के लिए
एल्गोरिथ्म लालची एल्गोरिथ्म के अनुसार काम करता
है : प्रत्येक पुनरावृत्ति पर, प्रशिक्षण सेट के इनपुट सबसेट के लिए, हाइपरप्लेन द्वारा अंतरिक्ष का ऐसा विभाजन (उनके समन्वय अक्षों में से एक के लिए ऑर्थोगोनल) का निर्माण किया गया है जो दो प्राप्त उपसमूह की विषमता के औसत माप को कम करता है। जब तक स्टॉप मानदंड पूरे नहीं हो जाते, तब तक प्राप्त होने वाली प्रत्येक सबसेट के लिए यह प्रक्रिया पुनरावर्ती रूप से की जाती है। हम इसे और अधिक औपचारिक रूप से लिखते हैं, इनपुट सेट
ए के लिए हमें जोड़ी <
साइन ,
साइन वैल्यू > मिलती है, कि विषमता का माप न्यूनतम होगा:
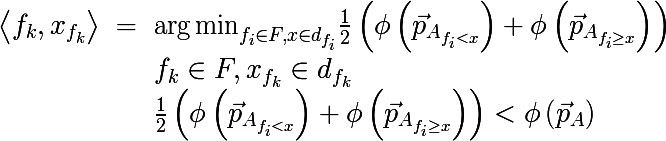
जहाँ
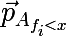
क्या सेट
ए के उपसमुच्चय से उपरोक्त प्रक्रिया द्वारा प्राप्त की जाने वाली प्रायिकता वेक्टर उन तत्वों से मिलकर होती है, जिनके लिए शर्त
<x पूरी होती है। इसके अलावा, यह मत भूलो कि विभाजन की औसत लागत मूल सेट की लागत से अधिक नहीं होनी चाहिए। आइए अब मूल चित्र पर वापस जाएं और वास्तव में क्या होता है, इस पर एक नज़र डालें, मूल डेटा को ऊपर वर्णित तरीके से विभाजित करें:
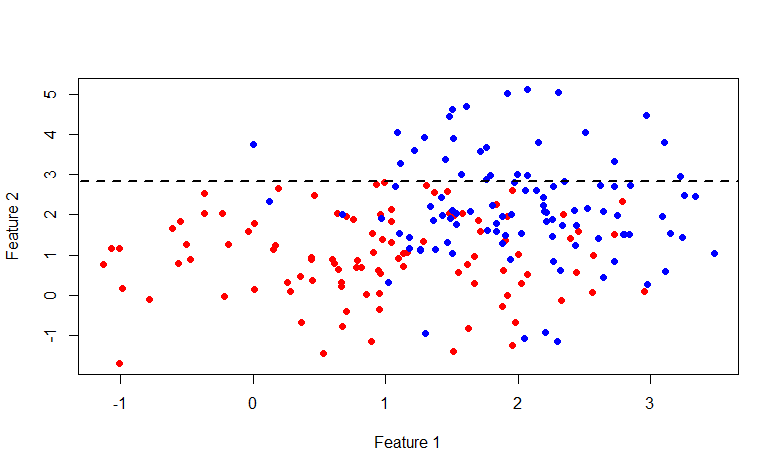
जैसा कि आप देख सकते हैं, लाइन
y = 2.840789 से ऊपर के सेट में पूरी तरह से नीले लेबल होते हैं, इसलिए यह केवल दूसरे सेट को तोड़ने के लिए समझ में आता है।
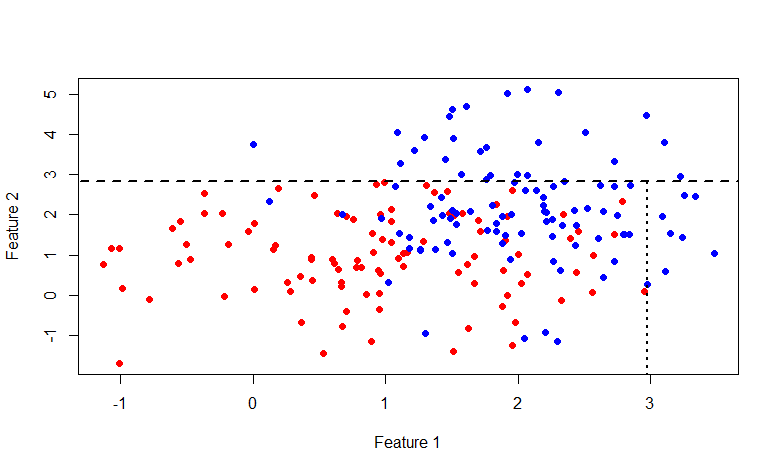
इस बार लाइन
x = 2.976719 । सामान्य तौर पर, किसी को भी इस चित्र में लिप्त होने में दिलचस्पी है, यहां आर कोड है:
विज़ुअलाइज़ेशन कोडrm(list=ls()) library(mvtnorm) labCount <- 100 lab1 <- rmvnorm(n=labCount, mean=c(1,1), sigma=diag(c(1, 1))) lab0 <- rmvnorm(n=labCount, mean=c(2,2), sigma=diag(c(0.5, 2))) df <- data.frame(x=append(lab1[, 1], lab0[, 1]), y=append(lab1[, 2], lab0[, 2]), lab=append(rep(1, labCount), rep(0, labCount))) plot(df$x, df$y, col=append(rep("red", labCount), rep("blue", labCount)), pch=19, xlab="Feature 1", ylab="Feature 2") giniIdx <- function(data) { p1 <- sum(data$lab == 1)/length(data$lab) p0 <- sum(data$lab == 0)/length(data$lab) return(p0*(1 - p0) + p1*(1 - p1)) } p.norm <- giniIdx getSeparator <- function(data) { idx <- NA idx.val <- NA cost <- p.norm(data) for(i in 1:(dim(data)[2] - 1)) { for(i.val in unique(data[, i])) { #print(paste("i = ", i, "; v = ", i.val, sep="")) cost.tmp <- 0.5*(p.norm(data[data[, i] < i.val, ]) + p.norm(data[data[, i] >= i.val, ])) if(is.nan(cost.tmp)) { next } if(cost.tmp < cost) { cost <- cost.tmp idx <- i idx.val <- i.val } } } return(c(idx, idx.val)) } s1 <- getSeparator(df) lines(c(-100, 100), c(s1[2], s1[2]), lty=2, lwd=2, type="l")
हम संभावित रोक मानदंडों को सूचीबद्ध करते हैं: अधिकतम नोड गहराई तक पहुंच गया है; विभाजन में प्रमुख वर्ग की संभावना एक निश्चित सीमा से अधिक है (मैं 0.95 का उपयोग करता हूं); सबसेट में तत्वों की संख्या एक निश्चित सीमा से कम है। नतीजतन, हमें पूरे सेट का एक विभाजन (हाइपर) आयतों में मिलता है, और प्रशिक्षण सेट के प्रत्येक ऐसे सबसेट को पेड़ के एक पत्ते के साथ जोड़ा जाएगा, और सभी आंतरिक नोड विभाजन के लिए शर्तों में से एक हैं; या दूसरे शब्दों में कुछ विधेय। वर्तमान नोड के लिए, बाएं बच्चे को उस सेट के उन तत्वों के साथ जोड़ा जाता है, जिसके लिए विधेय सत्य है, और सही एक, क्रमशः, उस विषय के लिए जिसके लिए विधेय झूठा वापस आता है। यह इस तरह दिखता है:

तो हमें एक पेड़ मिला, हम उस पर निर्णय कैसे ले सकते हैं? हमारे लिए यह निर्धारित करना मुश्किल नहीं होगा कि किसी विशेष निर्णय पेड़ के अनुसार, किसी भी इनपुट छवि को सेट करने वाले प्रशिक्षण के सबसेट में से कौन सा है। अगला, हम केवल इस सबसेट में प्रमुख वर्ग का चयन कर सकते हैं और इसे ग्राहक को वापस कर सकते हैं, या इस सबसेट में लेबल के प्रायिकता वितरण को वापस कर सकते हैं।
वैसे,
प्रतिगमन समस्या की कीमत पर। पेड़ बनाने की वर्णित विधि एक वर्गीकरण समस्या से एक प्रतिगमन कार्य में आसानी से बदल जाती है। इसके लिए, पूर्वानुमान त्रुटि के कुछ माप के साथ विषमता के उपाय को बदलना आवश्यक है, उदाहरण के लिए, मानक विचलन। और निर्णय लेते समय, प्रमुख वर्ग के बजाय, लक्ष्य चर का औसत मूल्य उपयोग किया जाता है।
ऐसा लगता है कि सब कुछ पेड़ों के साथ तय किया गया था। हम इस पद्धति के पेशेवरों और विपक्षों पर ध्यान नहीं देंगे;
विकिपीडिया पर
एक अच्छी सूची है। लेकिन अंत में, मैं रेखीय मॉडल और पेड़ों के बीच के अंतर के बारे में
एक परिचय पुस्तक से
एक सांख्यिकीय विवरण सीखना चाहता हूं।
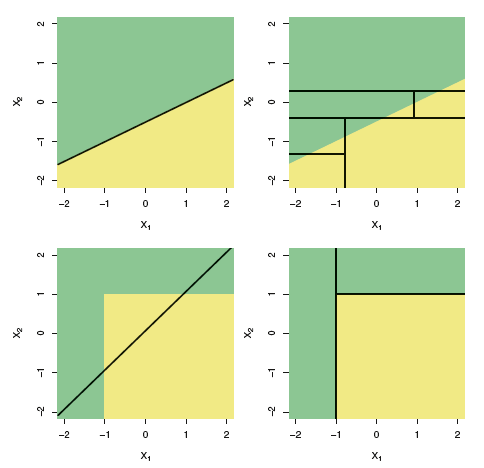
यह चित्रण एक रेखीय मॉडल और एक द्विआधारी निर्णय वृक्ष के बीच अंतर को दर्शाता है, जैसा कि आप रैखिक विभाज्यता के मामले में देखते हैं, सामान्य तौर पर, पेड़ एक साधारण रेखीय क्लासिफायरियर की तुलना में कम सटीक परिणाम दिखाएगा।
बूटस्ट्रैप कुलिंग या बैगिंग
चलो यादृच्छिक वन के अगले वैचारिक घटक पर चलते हैं। तो
BAG ging का नाम
B ootstrap
AG gregating से लिया गया है। आँकड़ों में, बूटस्ट्रैप का मतलब दोनों नमूना संभाव्यता वितरण के आँकड़ों की मानक त्रुटि और
मोंटे कार्लो पद्धति पर आधारित डेटा सेट से
नमूने के नमूने की एक विधि का आकलन करने के लिए समझा जाता है।
बूटस्ट्रैप नमूना अपने विचार में बहुत सरल है, और इसका उपयोग तब किया जाता है जब हम वास्तविक वितरण से बड़ी संख्या में नमूने प्राप्त करने में सक्षम नहीं होते हैं, और यह लगभग हमेशा ही होता है। माना कि हम आकार
n की टिप्पणियों के
m सेट प्राप्त करना चाहते हैं, लेकिन हमारे पास हमारे निपटान में केवल
n टिप्पणियों का एक सेट है। फिर हम चयनित सेट की वापसी (
पुनरावृत्ति या वापसी के साथ नमूना ) के साथ मूल सेट से
एन तत्वों के एक
परिवर्तनीय विकल्प के साथ
एम सेट उत्पन्न करते हैं।
N के बड़े मूल्यों के लिए, सेट को नमूना करके बूटस्ट्रैप द्वारा प्राप्त अद्वितीय तत्वों की संख्या प्रारंभिक सेट की अद्वितीय टिप्पणियों की कुल संख्या का
(1 - 1 / e)) 63.2% होगी । चलो,
मैं नमूना द्वारा बूटस्ट्रैप द्वारा प्राप्त
i- th सेट
हूं , हम इस
पर कुछ पैरामीटर का मूल्यांकन
करते हैं , और इस प्रक्रिया को कई बार दोहराते हैं। मानक त्रुटि बूटस्ट्रैप पैरामीटर अनुमान निम्नानुसार लिखे गए हैं:
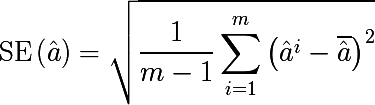
तो,
सांख्यिकीय बूटस्ट्रैप आपको कुछ वितरण पैरामीटर का आकलन करने में त्रुटि का मूल्यांकन करने की अनुमति देता है। लेकिन यह विषय से इस तरह की व्याकुलता है, लेकिन हम बूटस्ट्रैप नमूना विधि में रुचि रखते हैं।
अब कुछ गणितीय अपेक्षा और भिन्नता।
2 के साथ एक संभाव्यता वितरण से
मी स्वतंत्र रूप से चयनित तत्वों
x के सेट पर विचार करें। फिर नमूना औसत के बराबर होगा:
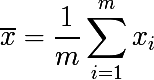
नमूना माध्य और विचरण के विपरीत वितरण पैरामीटर नहीं है, लेकिन यादृच्छिक चर का एक फ़ंक्शन, अर्थात। नमूना साधनों के कुछ संभाव्यता वितरण से एक यादृच्छिक चर भी है। और यह बदले में, फैलाव पैरामीटर है, जिसे निम्नानुसार व्यक्त किया गया है:
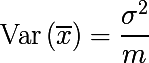
यह पता चलता है कि
एक यादृच्छिक चर के मूल्यों के सेट का औसत परिवर्तनशीलता को कम करता है । यह बूटस्ट्रैप नमूनों को एकत्र करने के विचार का आधार है। हम प्रशिक्षण सेट
डी (आकार
एन का भी) से आकार
n के एम बूटस्ट्रैप नमूने उत्पन्न करते हैं:
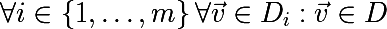
प्रत्येक बूटस्ट्रैप नमूने पर, हम
f मॉडल को प्रशिक्षित करेंगे और निम्नलिखित फ़ंक्शन को प्रस्तुत करेंगे, इस दृष्टिकोण को बूटस्ट्रैप एकत्रीकरण या बैगिंग कहा जाता है:
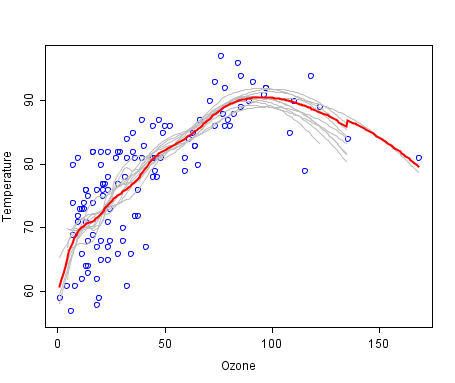
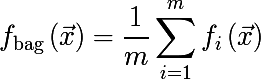 विकिपीडिया से निम्नलिखित ग्राफ
विकिपीडिया से निम्नलिखित ग्राफ द्वारा बैगिंग को चित्रित किया जा सकता है, जहां बैग-मॉडल को लाल रेखा द्वारा दिखाया गया है और कई अन्य मॉडलों का औसत है।
decorrelation
मुझे लगता है कि यह पहले से ही स्पष्ट है कि सिर्फ एक जंगल कैसे प्राप्त करें: हम कई बूटस्ट्रैप नमूने उत्पन्न करते हैं और उनमें से प्रत्येक पर निर्णय वृक्ष को प्रशिक्षित करते हैं। लेकिन एक छोटी सी समस्या है, लगभग सभी पेड़ कमोबेश एक ही संरचना के होंगे। चलो एक प्रयोग करते हैं,
दो वर्गों और 32 विशेषताओं के साथ एक
सेट लेते हैं, बूटस्ट्रैप नमूनों पर 1000 निर्णय पेड़ों का निर्माण करते हैं, और रूट नोड की परिवर्तनशीलता को देखें।
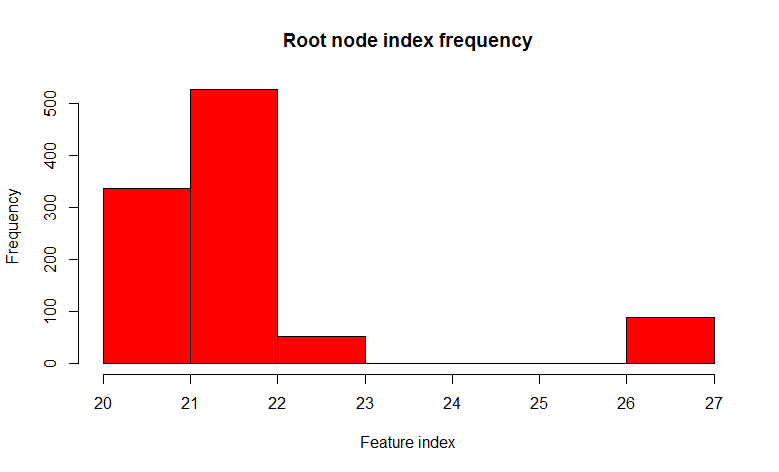
हम देखते हैं कि 1000 पेड़ों में से, 22 वां चिन्ह (जाहिर है कि फीचर का मूल्य समान है) 526 पेड़ों में पाया जाता है, और लगभग सभी बेटी में समान होता है। दूसरे शब्दों में, पेड़ एक दूसरे के सापेक्ष
सहसंबद्ध होते हैं। यह पता चला है कि यह 1000 पेड़ बनाने का कोई मतलब नहीं है, अगर केवल कुछ, और सबसे अधिक बार एक या दो, पर्याप्त हैं। और अब आइए एक पेड़ का निर्माण करते समय उपयोग करने का प्रयास करें, प्रत्येक नोड को विभाजित करते समय, सभी संकेतों के सेट से केवल कुछ छोटे यादृच्छिक संकेत, 32 में से 7 यादृच्छिक कहते हैं।
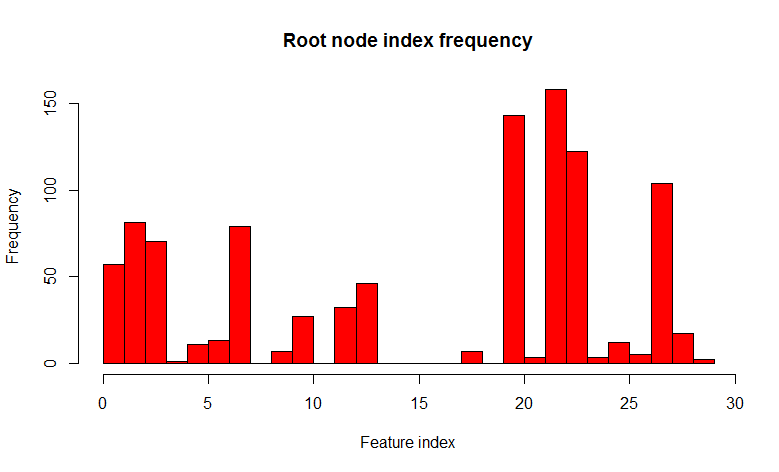
जैसा कि आप देख सकते हैं, वितरण पेड़ों की एक अधिक विविधता की दिशा में महत्वपूर्ण रूप से बदल गया है (वैसे, न केवल रूट नोड में, बल्कि बेटी नोड्स में भी), जो इस तरह के एक चाल का उद्देश्य था। अब 22 संकेत केवल 158 मामलों में पाए जाते हैं। "
32 संकेतों में
से 7 यादृच्छिक " की पसंद एक अनुभवजन्य अवलोकन (मैंने इस अवलोकन के लेखक को नहीं पाया है) द्वारा उचित है, और वर्गीकरण समस्याओं में यह आमतौर पर संकेतों की कुल संख्या का वर्गमूल है। दूसरे शब्दों में, पेड़ कम
सहसंबद्ध हो गए हैं, और प्रक्रिया को
सजावट कहा जाता है।
ऐसी विधि, जिसे सामान्य रूप से,
रैंडम सबस्पेस विधि कहा जाता है और इसका उपयोग न केवल निर्णय वृक्षों के लिए किया जाता है, बल्कि अन्य मॉडल जैसे तंत्रिका नेटवर्क के लिए भी किया जाता है।
सामान्य तौर पर, ऐसा कुछ साधारण फ्लैट जंगल की तरह दिखता है, और सजावट की जाती है।

कोड
आइए कार्यान्वयन के लिए आगे बढ़ें। एक बार फिर, मैं आपको याद दिलाना चाहता हूं कि मैंने जो उदाहरण दिया, वह यादृच्छिक वन का त्वरित कार्यान्वयन नहीं है, लेकिन केवल प्रकृति में शैक्षिक है, जिसे मॉडल के मुख्य विचारों को समझने में मदद करने के लिए डिज़ाइन किया गया है। उदाहरण के लिए,
यहां आपको एक उपयुक्त और फुर्तीला कार्यान्वयन का उदाहरण मिलेगा , लेकिन दुर्भाग्य से कम स्पष्ट है।
मैं उन टिप्पणियों को सम्मिलित करूंगा जहां कोड में सीधे आवश्यक हो, ताकि कक्षाओं को टुकड़ों में न तोड़ें।
मेरे मामले में अवलोकन की इकाई को निम्न वर्ग द्वारा दर्शाया गया है।
अवलोकन public class DataItem<T> { private T[] _input = null; private T[] _output = null; public DataItem() { } public DataItem(T[] input, T[] output) { _input = input; _output = output; } public T[] Input { get { return _input; } set { _input = value; } } public T[] Output { get { return _output; } set { _output = value; } } }
पेड़ के प्रत्येक नोड के लिए, वर्गीकरण के निर्णय लेने के लिए उपयोग किए जाने वाले विधेय के बारे में जानकारी संग्रहीत करना आवश्यक है।
ट्री नोड डेटा public class ClassificationTreeNodeData {
बाइनरी निर्णय पेड़ की कक्षा पर विचार करें।
बाइनरी निर्णय पेड़ public class ClassificationBinaryTree { private TreeNode<ClassificationTreeNodeData> _rootNode = null; private INorm<double> _norm = null;
आइए हम निर्णय पेड़ की कक्षा में उपयोग किए जाने वाले
मानदंड पर ध्यान दें।
दर इंटरफ़ेस public interface INorm<T> { double Calculate(T[] v); }
गनी सूचकांक internal class GiniIndex : INorm<double> { #region INorm<double> Members public double Calculate(double[] v) { return v.Sum(p => p*(1 - p)); } #endregion }
क्रॉस एन्ट्रापी internal class MetricsBasedNorm<T> : INorm<T> { private IMetrics<T> _m = null; internal MetricsBasedNorm(IMetrics<T> m) { _m = m; } #region INorm<T> Members public double Calculate(T[] v) { return _m.Calculate(v, v); } #endregion } public interface IMetrics<T> { /// <summary> /// Calculate value of metrics /// </summary> double Calculate(T[] v1, T[] v2); /// <summary> /// Get centroid/clusteroid of data /// </summary> T[] GetCentroid(IList<T[]> data); /// <summary> /// Calculate value of partial derivative by v2[v2Index] /// </summary> T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index); } internal class CrossEntropy : MetricsBase<double> { internal CrossEntropy() { } /// <summary> /// \sum_i v1_i * ln(v2_i) /// </summary> public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Length of v1 and v2 should be equal"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } double d = 0; for (int i = 0; i < v1.Length; i++) { d += v1[i]*Math.Log(v2[i] + Double.Epsilon); } return -d; } public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index) { return v2[v2Index] - v1[v2Index]; } }
खैर, यह केवल यादृच्छिक वन वर्ग पर विचार करने के लिए बनी हुई है।
बेतरतीब जंगल public class ClassificationRandomForest {
निष्कर्ष और संदर्भ
यदि आपने कोड पर गौर किया है, तो आप देख सकते हैं कि संरचना और शर्तों को
डॉट फॉर्मेट में लिखने के लिए पेड़ में एक फ़ंक्शन है
, जिसे ग्राफविस द्वारा कल्पना की जाती है । यदि आप
उपरोक्त सेट पर निम्नलिखित मापदंडों के साथ एक यादृच्छिक वन चलाते हैं:
ClassificationRandomForest crf = new ClassificationRandomForest( NormCreator.CreateByMetrics(MetricsCreator.CrossEntropy()), 10, 1, null, Convert.ToInt32(Math.Round(Math.Sqrt(ds.TrainSet.First().Input.Length))), 0.95, 1000, true ); crf.Train(ds.TrainSet);
फिर निम्नलिखित कोड हमें इस जंगल की कल्पना करने में मदद करेगा:
foreach (ClassificationBinaryTree tree in crf.Forest) { using (StreamWriter sw = new StreamWriter(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\" + (new DirectoryInfo(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\")).GetFiles().Count() + ".dot")) { tree.WriteDotFile(sw); sw.Close(); } }
dot.exe -Tpng "tree.dot" -o "tree.png"
आइए उनमें से कुछ को देखें, वे सजावट के कारण पूरी तरह से अलग हैं।
और अंत में, कुछ उपयोगी लिंक: