सिमुलेशन, सांख्यिकीय अनुमान और पुन: नमूने के लिए जल्दी से यादृच्छिक संख्या सरणियों को उत्पन्न करें

आजकल, मोंटे कार्लो विधियों का उपयोग करके सिमुलेशन का उपयोग परिचालन गतिविधि के लगभग सभी क्षेत्रों में किया जाता है जहां बाहरी दुनिया से प्राप्त आंकड़ों के विश्लेषण के आधार पर कई निर्णय लेने की आवश्यकता होती है। उसी समय, यादृच्छिक संख्या जनरेटर की गुणवत्ता, प्रदर्शन और पहुंच, जिसका उपयोग अमूर्त विधि को एक वास्तविक समस्या की विशेषताओं को देने के लिए किया जाता है जो एक विशेषज्ञ हल करता है, एक महत्वपूर्ण भूमिका निभाना शुरू करता है। जैसा कि मुझे हाल ही में पता चला है, यह समस्या समानांतर प्रोग्रामिंग के लिए संक्रमण में एक निर्णायक भूमिका निभाना शुरू करती है ... आप भी इस समस्या का सामना कर चुके हैं, और जानना चाहते हैं कि विंडोज में आप आवश्यक वितरण के साथ यादृच्छिक संख्याओं के सरणियों को कैसे प्राप्त कर सकते हैं?

/ * लेख अंग्रेजी में उद्धरणों की एक महत्वपूर्ण संख्या का उपयोग करता है, मैं पाठक के लिए भाषा प्रशिक्षण का पर्याप्त स्तर मानता हूं * /

मेरा एक ड्यूटी सर्विस एप्लिकेशन एक डेटाबेस से कारकों के लंबे अनुक्रम पर सिमुलेशन मॉडल चलाता है। विवरण में जाने के बिना, भविष्य के परिणामों की भविष्यवाणी में अनिश्चितता को कम करने के लिए अपने वास्तविक कार्यान्वयन के इतिहास से यादृच्छिकता के एक मजबूत तत्व के साथ एक दोहराए जाने वाले द्विआधारी (दो-स्रोत) प्रक्रिया की संभाव्य विशेषताओं का अध्ययन करने के लिए हाल ही में एक कार्य उत्पन्न हुआ। प्रक्रिया के कार्यान्वयन को एक दूसरे से स्वतंत्र माना जाता है और समान रूप से (सामान्य रूप से) वितरित किया जाता है, प्रक्रिया को स्थिर माना जाता है। लक्ष्य - संभव के रूप में एन क्रमिक प्रक्रिया कार्यान्वयन के परिणामों की सबसे सटीक भविष्यवाणी - लंबाई एन की अवधि में सकारात्मक प्रक्रिया कार्यान्वयन की औसत और न्यूनतम अपेक्षित आवृत्तियों का अनुमान लगाती है।

यहां आप विश्वास स्तर की गणना के साथ मानक सांख्यिकीय दृष्टिकोण का उपयोग कर सकते हैं, जिस पर एक यादृच्छिक चर के बोध अपने मानक विचलन के कश्मीर मूल्यों से अधिक इसकी अपेक्षा से विचलित नहीं करते हैं। यह दृष्टिकोण प्रायिकताओं ( बर्नौली प्रमेय ) की आवृत्ति अभिसरण के विचार पर आधारित है। बेशक, डेटाबेस में दर्ज कई सौ हजार प्रक्रिया कार्यान्वयनों के आधार पर औसत मूल्यों की गणना करना बहुत ही आकर्षक है, लेकिन चूंकि मेरे पास सबमिशन एन (कई दसियों के आदेश) की लंबाई पर प्रतिबंध है, इसलिए सीमित नमूने पर प्रक्रिया की यादृच्छिक प्रकृति मुझे निश्चित रूप से विचलन के रूप में आश्चर्यचकित करेगी। औसत। यही कारण है कि मुझे निश्चित डिग्री के साथ यह जानने की जरूरत है कि किसी दिए गए एन के लिए औसत अपेक्षित आवृत्ति से अधिकतम संभव विचलन "निर्धारित" होना चाहिए।

मैंने सांख्यिकीय बूटस्ट्रैपिंग (बूटस्ट्रैपिंग) की विधि द्वारा आवश्यक अनुमान प्राप्त करने का निर्णय लिया - उदाहरणों के मुख्य सेट से मोंटे कार्लो विधि का उपयोग करके एन अहसास से नमूनों की कई पीढ़ी। विधि का सार उपलब्ध नमूने से पर्याप्त संख्या में छद्म नमूने बनाने के लिए है, जिसमें तत्वों के मूल सेट के यादृच्छिक संयोजनों से मिलकर बनता है (परिणामस्वरूप, कुछ प्रारंभिक तत्व एक छद्म नमूने में कई बार हो सकते हैं, जबकि अन्य पूरी तरह से अनुपस्थित हो सकते हैं), और प्रत्येक छद्म नमूने के लिए प्राप्त किया जाता है। उनके बिखराव का अध्ययन करने के लिए विश्लेषण किए गए सांख्यिकीय विशेषताओं के मूल्यों को निर्धारित करें।

प्रारंभिक अनुमानों के अनुसार, मुझे हजारों पैरामीटर उपसमूहों में से प्रत्येक के लिए ~ 10 मिलियन छद्म नमूने उत्पन्न करने की आवश्यकता होगी। डेटा और अन्य कारकों की मात्रा को देखते हुए, हम दसियों घंटे के सर्वर कंप्यूटिंग समय के बारे में बात कर रहे हैं। विजुअल बेसिक 6 में, एक प्रोटोटाइप एप्लिकेशन सिम्युलेटर लिखा और परीक्षण किया गया था। हालांकि, बहु-थ्रेडेड कॉम्बैट संस्करण को संकलित करने के बाद, यह अचानक पता चला कि जब सिमुलेशन को कई थ्रेड्स में लॉन्च किया गया था, तो सीपीयू कोर का लोड अपेक्षित 100% के बजाय केवल 5% था।

इंटेल Vtune एम्पलीफायर प्रोफाइलर में बुनियादी हॉटस्पॉट विश्लेषण ने कुछ भी असामान्य नहीं दिखाया। मुझे यकीन था कि सिम्युलेटर को काम के साथ सभी थ्रेड्स को पूरी तरह से लोड करना चाहिए, क्योंकि कोड में अंकगणितीय संचालन और यादृच्छिक सूचकांकों द्वारा मेमोरी एक्सेस के अलावा कुछ भी शामिल नहीं था:

For k = 1 To NumIters Randomize For i = 1 To NumPockets NumFired = 0 For j = 1 To chainLength ind = d + Int(B * Rnd) NumFired = NumFired + FiredOrNot(ind) Next j Tmp = NumFired / chainLength If Tmp < MinProb Then MinProb = Tmp If Tmp > MaxProb Then MaxProb = Tmp Values(i) = Tmp TotalFired = TotalFired + NumFired Next i AvgProb = TotalFired / (k * NumPockets) / chainLength Next k 

क्या यह कोड मेमोरी बैंडविड्थ से जुड़ा हुआ है?! और फिर हमें मल्टी-मेगाबाइट प्रोसेसर कैश की आवश्यकता क्यों है, वे सामना क्यों नहीं कर सकते? समस्या ने मुझे कुछ दिनों तक परेशान किया। बेलगाम लॉन्च किए गए कॉनक्यूरेबिलिटी एनालिसिस ने वीबी सिस्टम लाइब्रेरी के बॉल्स में कहीं न कहीं भारी गिरावट का खुलासा किया, लेकिन मुझे यह नहीं दिखा सका कि ये महंगा सिस्टम फंक्शन कहां से बुलाए जाते हैं:



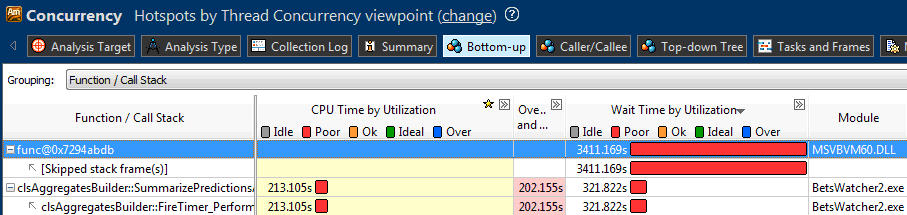
अंत में, प्रयोगात्मक रूप से, मुझे पता चला कि समस्या रैंड ऑपरेटर के साथ थी! जाहिर है, डेवलपर्स द्वारा रैंड का समानांतर उपयोग प्रदान नहीं किया जाता है; शायद Microsoft कार्यान्वयन कुछ प्रकार के आंतरिक लंबित ताले का उपयोग करता है। वास्तव में, अनुप्रयोग को गति देने के बजाय रैंड को समानांतर करना थाउज़ेंड्स को धीमा कर देता है! मुझे लगता है कि VBA का उपयोग करके MS Office उत्पादों के लिए एक समान व्यवहार विशिष्ट होगा। इससे पहले कभी भी यादृच्छिक पूर्णांक सूचक उत्पन्न करने का मुद्दा मेरे लिए इतना प्रासंगिक नहीं रहा है! मैंने यादृच्छिक संख्याओं के सरणियों के लिए तैयार पुस्तकालयों की तलाश करने का निर्णय लिया।

चुनाव अपने सांख्यिकीय कार्यों पैकेज के साथ इंटेल® मैथ कर्नेल लाइब्रेरी पर गिर गया।


MKL परीक्षण मोड में उपलब्ध है। वर्तमान में (संस्करण 11.02), 11 बुनियादी यादृच्छिक चर जनरेटर, 12 निरंतर, 11 असतत आउटपुट वितरण उपलब्ध हैं। मेरे लिए बहुत महत्वपूर्ण निकला, डेवलपर पुस्तकालय की धागा सुरक्षा की गारंटी देता है, इसके अलावा, यह बहु-थ्रेडेड मोड में उपयोग किए जाने पर अपने उत्पाद के फायदे बताता है ... एमकेएल प्रलेखन में, मेरा ध्यान निम्नलिखित अनुभाग पर आकर्षित किया गया था।

गैर-नियतात्मक यादृच्छिक संख्या जनरेटर (केवल RDRAND- आधारित जनरेटर) [AVX], [IntelSWMan]। आप गैर-निर्धारक यादृच्छिक संख्या जनरेटर का उपयोग केवल तभी कर सकते हैं जब अंतर्निहित हार्डवेयर इसका समर्थन करता है। यह जानने के लिए कि कैसे एक इंटेल सीपीयू एक गैर-निर्धारक यादृच्छिक संख्या जनरेटर का समर्थन करता है, उदाहरण के लिए, अध्याय 8: [AVX] या अध्याय 4 में पोस्ट -32 एनएम प्रोसेसर निर्देश [BMT] में RdRand निर्देश उपयोग।

मैं लंबे समय से इस "लोहा" सुविधा की कोशिश करना चाहता था, लेकिन, दुर्भाग्य से, यह पता चला कि मेरे प्रोसेसर एक हार्डवेयर यादृच्छिक संख्या जनरेटर से लैस नहीं हैं। उपरोक्त के अलावा, एमकेएल पैकेज की एक महत्वपूर्ण विशेषता अधिकांश प्रोग्रामिंग भाषाओं में प्रति ऑपरेटर कॉल के लिए एक यादृच्छिक मूल्य प्राप्त करने के सामान्य अभ्यास के विपरीत, यादृच्छिक संख्या धाराओं के ब्लॉक पीढ़ी का प्रतिमान है।

Xeon Phi coprocessor आर्किटेक्चर का उपयोग करके सिमुलेशन के लिए MKL VSL से यादृच्छिक संख्याओं का उपयोग करने के काम के उदाहरण, उदाहरण के लिए, शुओ ली का केस स्टडी: मोंटे कार्लो यूरोपीय विकल्प पर उच्च प्रदर्शन प्राप्त करना, स्टेपवाइज ऑप्टिमाइज़ेशन फ्रेमवर्क का उपयोग करना , पहले से ही नेटवर्क पर उपलब्ध हैं। शायद कोई इस लेख का अनुवाद करना चाहता है? इसमें, यादृच्छिक संख्या की अनुक्रमिक पीढ़ी से "स्ट्रीमिंग" में संक्रमण के दौरान, एक अच्छी गति वृद्धि दर्ज की जाती है:

C ++ TR1 से RNG को इंटेल MKL में बदलने से न केवल मूल कोड पर 5.53X सुधार हुआ, बल्कि इसने इनलाइन फ़ंक्शन कॉल करने में भी सक्षम किया और आंतरिक लूप में कोड को सदिश किया ...

दो 8-कोर सैंडी ब्रिज @ २.६ हर्ट्ज ज़ीओन्स की तुलना में एमआईसी आर्किटेक्चर के लिए रिकॉम्पेलिंग और भी अधिक विकास प्रदान करता है:

वही कार्यक्रम जिसने होस्ट सिस्टम पर पूरा करने के लिए 44 सेकंड का समय लिया था, अब यह केवल 5 सेकंड से भी कम समय में पूरा हो जाता है, एक त्वरित 8.82X सुधार।

हालांकि, लेख से मुझे अभी तक समझ में नहीं आया कि $ 4129 के लिए Phi लेखक ने किस मॉडल का उपयोग किया, जाहिरा तौर पर, 7120X (16GB, 1.238 GHz, 61 कोर)। यह समय है, शायद, Phi लेने के लिए, जिनके पास पहले समय नहीं है, शूरवीरों की लैंडिंग का इंतजार नहीं कर रहे हैं, दोस्तों ;-) युद्ध में प्रयास करना दिलचस्प होगा और "अपनी फ़ि कहो"।

किसी भी मामले में, हम अब यादृच्छिक संख्या ब्लॉक बनाने के लिए MKL के दृष्टिकोण में रुचि रखते हैं। सबसे पहले, vslNewStream को कॉल करके, दी गई विशेषताओं के साथ एक यादृच्छिक संख्या स्ट्रीम जेनरेटर बनाया जाता है, उदाहरण के लिए, बेस जनरेटर VSL_BRNG_SFMT19937 (A SIMD- ओरिएंटेड फास्ट मेर्सन लिस्टर सिस्टर स्यूडोरैंडम नंबर जनरेटर) का नाम आकर्षक लगता है। तब इस जनरेटर का उपयोग (और अलग-अलग धाराओं से) किया जा सकता है ताकि वांछित वितरण और डेटा प्रकार के साथ यादृच्छिक संख्याओं के अनुक्रम के साथ आवंटित मेमोरी ब्लॉक को सीधे भरा जा सके। एक कॉल, उदाहरण के लिए, virnguniform (विधि, स्ट्रीम, एन, आर, ए, बी) धारा एन जनरेटर के आधार पर सरणी आर को समान रूप से वितरित बी से यादृच्छिक मूल्यों के साथ सरणी आर पर भरता है। काम के बाद, स्ट्रीम को vslDeleteStream कहकर हटा दिया जाना चाहिए।

यादृच्छिक संख्याओं के समानांतर उपयोग / पीढ़ी में महत्वपूर्ण पहलू हैं, छद्म यादृच्छिक जनरेटरों की परिमित अवधि के कारण, हमारे कंपोजर सेर्गेई मादानोव और आंद्रेई नाराइकिन द्वारा " मोंटे कार्लो एप्रोच इवनिंग और फास्टर भी बनाना " लेख में खूबसूरती से चित्रित किया गया है। जिज्ञासु के लिए, मैं एक उद्धरण (बिना अनुवाद के) उद्धृत करता हूं:
यह कहा जाना चाहिए कि उनकी MKL लाइब्रेरी में, इंटेल के स्मार्ट लोगों ने बाद के दृश्यों में विभाजन के लिए स्किप-फॉरवर्ड और लीपफ्रॉग दोनों तरीकों को लागू किया। हालांकि, मेरे काम के हिस्से के रूप में, हालांकि एक मूल जनरेटर से कई धाराओं का उपयोग किया जाता है, एक दूसरे से धाराओं की पूर्ण सांख्यिकीय स्वतंत्रता के लिए कोई आवश्यकता नहीं है, क्योंकि वे स्वतंत्र रूप से और डेटा के विभिन्न उपसमूहों पर उपयोग किए जाते हैं। इसलिए, मेरे लिए मुख्य तकनीकी कठिनाई सी और फोरट्रान द्वारा तेज किए गए एमकेएल इंटरफेस को विज़ुअल बेसिक प्रोजेक्ट से जोड़ रही है। Microsoft * Office Excel से Intel® MKL का उपयोग करने का लेख बचाव में आता है, जो वर्णन करता है कि MKL का उपयोग करके एक रैपर dll कैसे उत्पन्न किया जाए, और Excel से MLK फ़ंक्शंस (stdcall कन्वेंशन) को कॉल का उदाहरण दिया जाता है।

अवधारणा यह है: आप MKL बिल्डर को स्वचालित रूप से एक dll उत्पन्न करने के लिए कह सकते हैं जो आपके द्वारा दिए गए कॉलिंग कन्वेंशन के साथ MKL फ़ंक्शन की मनमानी सूची का निर्यात करता है। बेशक, आप वीसी ++ में अपना स्वयं का डीएल प्रोजेक्ट बना सकते हैं, लेकिन मुझे यह प्रतीत हुआ कि स्वचालित पीढ़ी एक अधिक सार्वभौमिक तरीका है, और यहां तक ​​कि आवश्यक फ़ाइल को तेज़ी से प्राप्त करने में मदद करता है। यह जल्दी से स्पष्ट हो गया कि लेख पुराना था, और यहां तक ​​कि परीक्षण कमांड nmake libia32 सूत्रण = अनुक्रमिक इंटरफ़ेस = stdcall निर्यात = user_example_list नाम = mkl_custom कई कारणों से तुरंत क्रैश हो गया। मैंने mvc \ Tools \ बिल्डर \ फ़ोल्डर में msvcrt.lib फ़ाइल जोड़कर समस्याओं में से एक को हल किया। अलग-अलग संदेशों के बाहरी आनंद के लिए अलग-अलग आनंद लिया ___security_cookie ।

Microsoft की सिफारिशों का उपयोग करते हुए और आधे दिन की खोज में मारे जाने के बाद, मैं इस नतीजे पर पहुंचा कि आपको बिल्डर फोल्डर में मेकफाइल को संशोधित करने की जरूरत है। ठीक है, तो एक खरोंच के साथ तंत्र ने काम किया, और nmake libia32 सूत्रण = समानांतर इंटरफ़ेस = stdcall निर्यात = vml_vsl_stdcall_example_list नाम = mkl_custom जारी करके , मैं एक 38-मेगाबाइट गतिशील पुस्तकालय का भाग्यशाली स्वामी बन गया, जिसमें वेक्टर सांख्यिकीय पुस्तकालय के सभी कार्य शामिल थे। अपने आप में स्वस्थ पूंजीवादी लालच पर काबू पाने के बाद, मैंने लाइब्रेरी में केवल 3 आवश्यक कार्य छोड़ दिए, जिसके बाद आकार कुछ मेगाबाइट तक घट गया।

अब कॉलिंग कोड के बारे में। VB6 और VBA में, आवश्यक कार्यों को इस तरह घोषित किया जाना चाहिए:

 Public Declare Function vslNewStream Lib "mkl_custom.dll" (ByRef StreamPtr As Long, ByVal brng As Long, ByVal seed As Long) As Long Public Declare Function vslDeleteStream Lib "mkl_custom.dll" (ByRef StreamPtr As Long) As Long Public Declare Function viRngUniform Lib "mkl_custom.dll" (ByVal method As Long, ByVal StreamPtr As Long, ByVal n As Long, ByRef Data As Long, ByVal A As Long, ByVal B As Long) As Long 

परीक्षण के रूप में, आइए आधार जनरेटर VSL_BRNG_MCG31 (एक 31-बिट गुणक अनुरूपता जनरेटर) का उपयोग करके 1 से 10,000 तक (10,000 सहित नहीं) से 5 मिलियन यादृच्छिक पूर्णांक सूचक की एक सरणी उत्पन्न करने का प्रयास करें।

 Dim i&, theStream&, v&(), res&, t! Dim theStream As Long ReDim v(1 To 5000000): res = vslNewStream(theStream, VSL_BRNG_MCG31, 777) t = Timer For i = 1 To 100 res = viRngUniform(VSL_RNG_METHOD_UNIFORM_STD, theStream, 5000000, v(1), 1, 10000) Next i Debug.Print Timer - t res = vslDeleteStream(theStream) 

रनटाइम - 1.19 सेकंड। वैसे, VSL_BRNG_SFMT19937 जनरेटर जो SSE का उपयोग करना जानता है, वही कार्य 0.99 सेकंड में कर सकता है। ठीक है, मुख्य कोड के लिए आवश्यक संचालन की कॉल जोड़ें, और प्रोसेसर लोड की निगरानी करें:



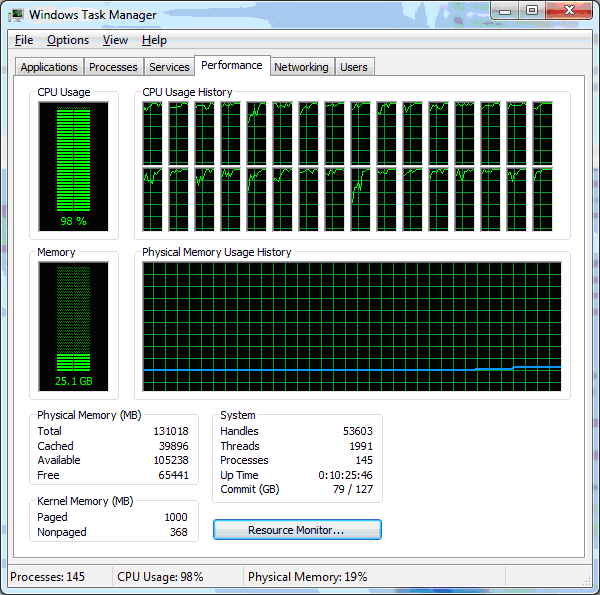
बिंगो, पूर्ण डाउनलोड! क्यूआरएंड पैकेज का उपयोग करके एक जीपीजीपीयू कार्यान्वयन करने का विचार था, जिनके फायदे स्पष्ट रूप से एनवीडिया द्वारा इंगित किए गए हैं:

इंटेल एमकेएल की तुलना में धधकते तेज कू्रंद प्रदर्शन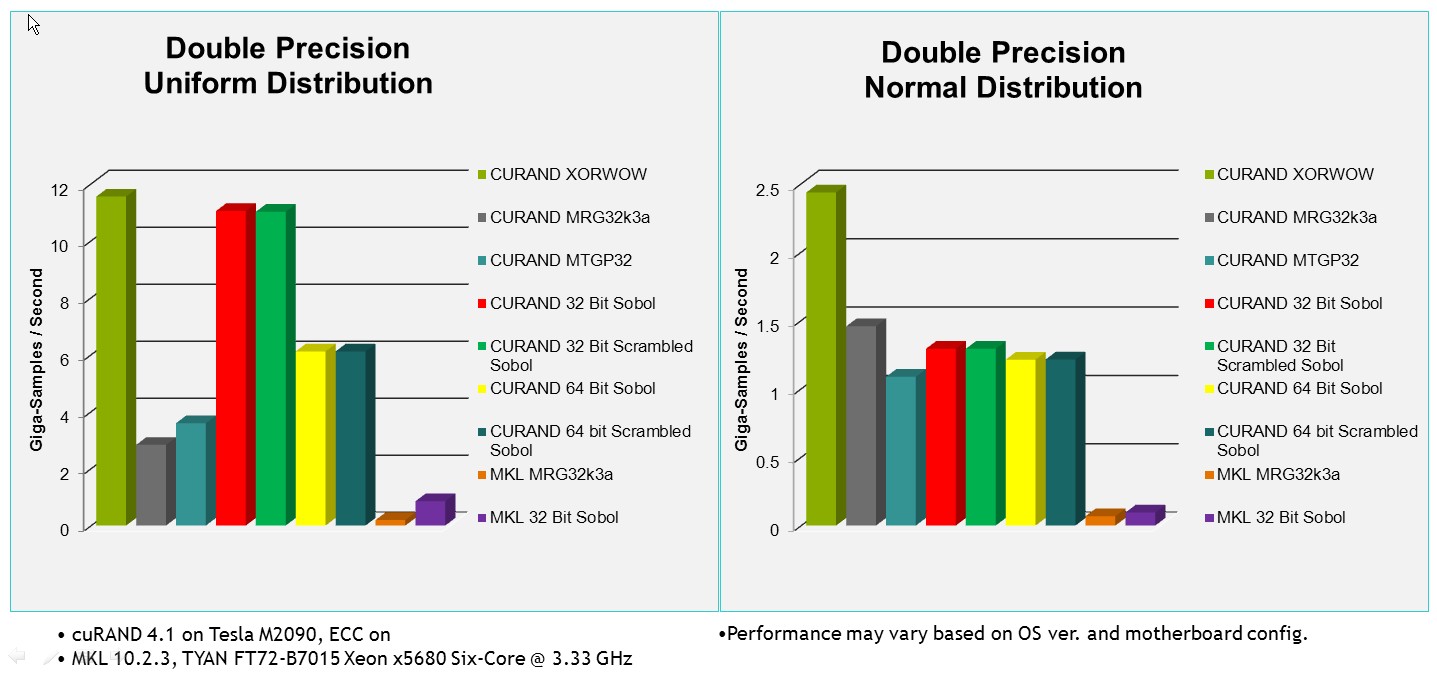


हालांकि, प्रारंभिक लक्ष्य एमकेएल के साथ हासिल किया गया था, और अभी भी कुडा संस्करण का परीक्षण करने के लिए कोई खाली समय नहीं है। :-)

संक्षेप में: हमने यादृच्छिक संख्याओं के समानांतर पीढ़ी में कुछ समस्याओं के बारे में सीखा, और इंटेल एमकेएल का उपयोग करके उन्हें हल करने के बारे में व्यावहारिक सिफारिशें प्राप्त कीं। आप आधुनिक विज़ुअल स्टूडियो की किसी भी भाषा से इस शक्तिशाली पुस्तकालय का उपयोग कर सकते हैं - C ++, C #, VB, साथ ही विज़ुअल फ़ोर्ट्रान, और, किसी भी वातावरण से आवाज़ वाली तकनीक का उपयोग करके, जो बाहरी dll को कॉल कर सकते हैं, उदाहरण के लिए, VB6, VBA, LabView, Matlab और कई अन्य शामिल हैं।

आपका ध्यान के लिए धन्यवाद!