
यह माना जाता है कि बहु-चरण मिसाइल के इष्टतम लेआउट में, प्रत्येक चरण में 4 किमी / सेकंड की विशेषता गति (डेल्टा-वी) का मार्जिन होना चाहिए। यह माना जाता है कि इष्टतम प्रारंभिक थ्रस्ट-टू-वेट अनुपात 1.2। लेकिन इन विचारों की किसी तरह पुष्टि होनी चाहिए। मैं यह भी प्रदर्शित करना चाहता था कि रॉकेट मल्टीस्टेज क्यों हैं। सूत्र अच्छे हैं, लेकिन कुछ और की जरूरत है, और खेल और प्रतियोगिताएं आदर्श रूप में इस तरह के अनुकूल हैं। इस प्रकार शैक्षिक / गेमिंग कार्यक्रम की परियोजना का जन्म हुआ, जिसका नाम "आपका
पीएन बढ़ाना" था
समस्या का बयान और सरलीकरण स्वीकार किए जाते हैं
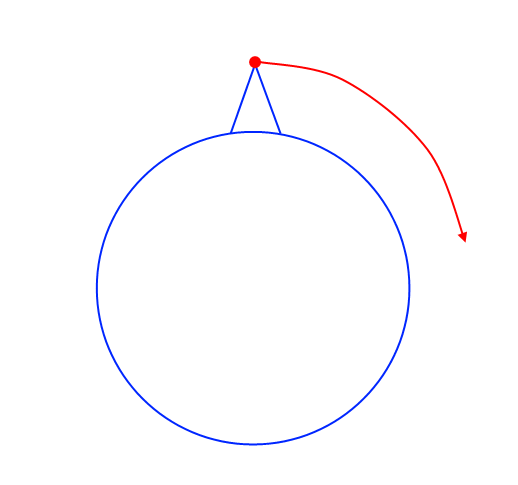
वस्तुतः ग्रहों से दूर एक निर्वात में रॉकेट को गति देना मुझे अटपटा लगता था। इसलिए, कार्य पृथ्वी से शुरू होगा। वायुगतिकीय ड्रैग की गणना और सतह से कक्षा में जाना जटिल लग रहा था, इसलिए रॉकेट, जैसा कि न्यूटन के विचार प्रयोग में है, निर्वात में "उच्च पर्वत" से लॉन्च होगा:
इनपुट पैरामीटर
निम्नलिखित मापदंडों को इनपुट के रूप में चुना गया था:
- इंजनों का सूखा वजन, किग्रा।
- इंजनों की संख्या, टुकड़े।
- इंजन किलोवाट में जोर देता है।
- एक इंजन द्वारा सभी ईंधन घटकों का उपभोग, प्रति किलोग्राम किलोग्राम।
- ईंधन का द्रव्यमान, किग्रा।
अनुमानित और संबंधित पैरामीटर
जिन लोगों को रॉकेटरी में थोड़ी भी दिलचस्पी है, वे पूछ सकते हैं कि Tsiolkovsky सूत्र में प्रयुक्त विशिष्ट आवेग कहाँ गायब हो गया? वास्तव में, वह कहीं नहीं गया है। विशिष्ट आवेग निहित रूप से इंजन जोर और ईंधन की खपत में निहित है। एमआई कर्षण के लिए आनुपातिक है और ईंधन की खपत के विपरीत आनुपातिक है। अधिक से अधिक जोर और कम ईंधन की खपत, अधिक से अधिक एअर इंडिया।
टन में इंजन जोर को किलोटन में जोर देकर परिवर्तित किया जा सकता है, इसे 9.81 से गुणा किया जा सकता है।
टैंक, एडेप्टर और अन्य सहायक संरचनाओं के द्रव्यमान को "ऑफहैंड" माना जाता है, जो ईंधन द्रव्यमान का 10% है और इसे "परजीवी द्रव्यमान" कहा जाता है। यह काफी गंभीर सरलीकरण है, क्योंकि वास्तव में यह पैरामीटर रॉकेट की समग्र दक्षता को प्रभावित करता है और विभिन्न रॉकेटों में भिन्न होता है। हल्का टैंक, एडेप्टर और अन्य संरचनाएं, कम परजीवी द्रव्यमान को एक रॉकेट द्वारा उठाया जाना चाहिए।
सकल और खाली जनता की गणना ज्ञात मापदंडों के आधार पर की जाती है। खाली द्रव्यमान सभी इंजनों का द्रव्यमान और परजीवी द्रव्यमान है, कुल द्रव्यमान खाली द्रव्यमान और ईंधन का द्रव्यमान है
गुरुत्वाकर्षण नुकसान की गणना नीचे विस्तार से दिखाई गई है।
पैरामीटर को ध्यान में नहीं रखा गया है
- कार्यों को सरल बनाने के लिए ध्यान नहीं दिया जाता है:
- हवा पर घर्षण नुकसान।
- वायुमंडलीय दबाव के आधार पर मसौदे में बदलाव।
- चढ़ाई।
- चरणों की जुदाई के लिए समय की हानि।
- अधिकतम गति सिर पर इंजन जोर में परिवर्तन।
- केवल एक लेआउट को ध्यान में रखा जाता है - चरणों की एक क्रमिक व्यवस्था के साथ।
भौतिकी और गणित का एक सा
गति गणना
मॉडल में रॉकेट का त्वरण इस प्रकार है:

उड़ान की ऊंचाई को स्थिर माना जाता है। फिर रॉकेट थ्रस्ट को दो अनुमानों में विभाजित किया जा सकता है:
Fx और
Fy ।
Fy mg के बराबर होना चाहिए, ये हमारे गुरुत्वाकर्षण के नुकसान हैं, और
Fx वह बल है जो रॉकेट को गति देगा।
एफ निरंतर है, यह इंजन जोर है, ईंधन की खपत के कारण
मीटर बदल रहा है।
प्रारंभ में, गति के रॉकेट समीकरण को विश्लेषणात्मक रूप से हल करने का एक प्रयास था। हालांकि, यह सफल नहीं था, क्योंकि गुरुत्वाकर्षण का नुकसान रॉकेट की गति पर निर्भर करता है। आइए एक विचार प्रयोग करें:
- उड़ान की शुरुआत में, रॉकेट केवल लॉन्च पैड से नहीं निकलता है अगर इंजन का जोर रॉकेट के वजन से कम है।
- त्वरण के अंत में, रॉकेट भी बल mg के साथ पृथ्वी की ओर आकर्षित होता है , लेकिन इससे कोई फर्क नहीं पड़ता, क्योंकि इसकी गति ऐसी होती है कि इसके गिरने का समय नहीं होता है, और जब यह एक गोलाकार कक्षा में प्रवेश करता है, तो यह लगातार पृथ्वी पर गिरता रहेगा, "इससे गायब" होता है। गति के लिए।
यह पता चलता है कि वास्तविक गुरुत्वाकर्षण नुकसान रॉकेट के द्रव्यमान और गति का एक कार्य है। एक सरलीकृत सन्निकटन के रूप में, मैंने गुरुत्वाकर्षण के नुकसान के बारे में विचार करने का निर्णय लिया:
 V1
V1 पहली ब्रह्मांडीय गति है।
अंतिम गति की गणना करने के लिए, संख्यात्मक सिमुलेशन का उपयोग करना आवश्यक था। एक सेकंड की वेतन वृद्धि में, निम्नलिखित गणना की जाती है:
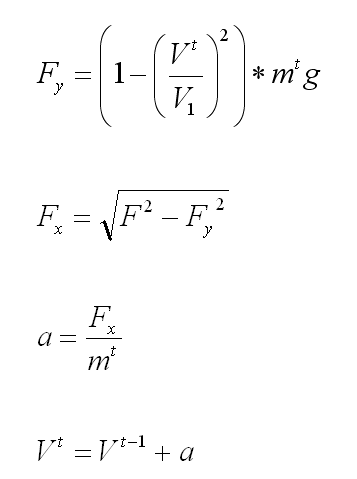
सुपरस्क्रिप्ट टी वर्तमान में दूसरा है, टी -1 पिछले एक है।
या एक प्रोग्रामिंग भाषा मेंfor (int time = 0; time < iBurnTime[stage]; time++) { int m1 = m0 - iEngineFuelUsage[stage] * iEngineQuantity[stage]; double ms = ((m0 + m1) / 2); double Fy = (1-Math.pow(result/7900,2))*9.81*ms; if (Fy < 0) { Fy = 0; } double Fx = Math.sqrt(Math.pow(iEngineThrust[stage] * iEngineQuantity[stage] * 1000, 2)-Math.pow(Fy, 2)); if (Fx < 0) { Fx = 0; } result = (result + Fx / ms); m0 = m1; }
अधिकतम पेलोड गणना
प्रत्येक अनुमेय पेलोड के लिए अंतिम गति जानने के बाद, हम पेलोड को अधिकतम करने की समस्या को हल कर सकते हैं क्योंकि एक अरेखीय समीकरण की जड़ को खोजने की समस्या है।

इस समीकरण को हल करने के लिए मुझे यह सबसे सुविधाजनक लग रहा था:
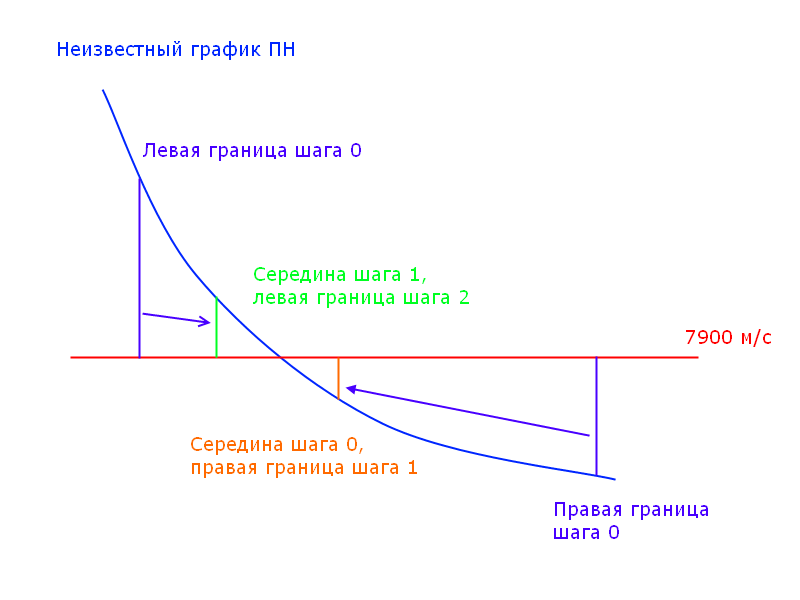
कोड पूरी तरह से मानक है public static int calculateMaxPN(int stages) { deltaV = new double[5]; int result = 0; int PNLeft = 50; while (calculateVelocity(PNLeft, stages, false) > 7900) { PNLeft = PNLeft + 1000; } System.out.println(calculateVelocity(PNLeft, stages, false)); int PNRight = PNLeft - 1000; double error = Math.abs(calculateVelocity(PNLeft, stages, false) - 7900); System.out.println(" " + Double.toString(PNLeft) + "; " + Double.toString(PNRight) + "; " + Double.toString(error)); boolean calcError = false; while ((error / 7900 > 0.001) && !calcError) { double olderror = error; if (calculateVelocity((PNLeft + PNRight) / 2, stages, false) > 7900) { PNRight = (PNLeft + PNRight) / 2; } else { PNLeft = (PNLeft + PNRight) / 2; } error = Math.abs(calculateVelocity((PNLeft + PNRight) / 2, stages, false) - 7900); System.out.println(" " + Double.toString(PNLeft) + "; " + Double.toString(PNRight) + "; " + Double.toString(error)); if (Math.abs(olderror - error) < 0.0001) {
और खेलने के लिए?
अब, सैद्धांतिक भाग के बाद, आप खेल सकते हैं।
परियोजना
GitHub पर स्थित है । एमआईटी लाइसेंस, उपयोग और स्वास्थ्य के लिए संशोधित, और वितरण भी स्वागत है।
अगर अचानक किसी को इंस्टॉलेशन निर्देश की आवश्यकता होती है- लिंक का पालन करें https://github.com/lozga/rocketcalc
- "डाउनलोड ज़िप" बटन का उपयोग करके संग्रह डाउनलोड करें।
- किसी फ़ोल्डर में खोलना।
- यदि आपके पास जावा स्थापित नहीं है, तो इसे कार्यालय से इंस्टॉल करें । साइट ।
- RocketStageCalc.jar फ़ाइल चलाएँ।
मुख्य और एकमात्र प्रोग्राम विंडो:
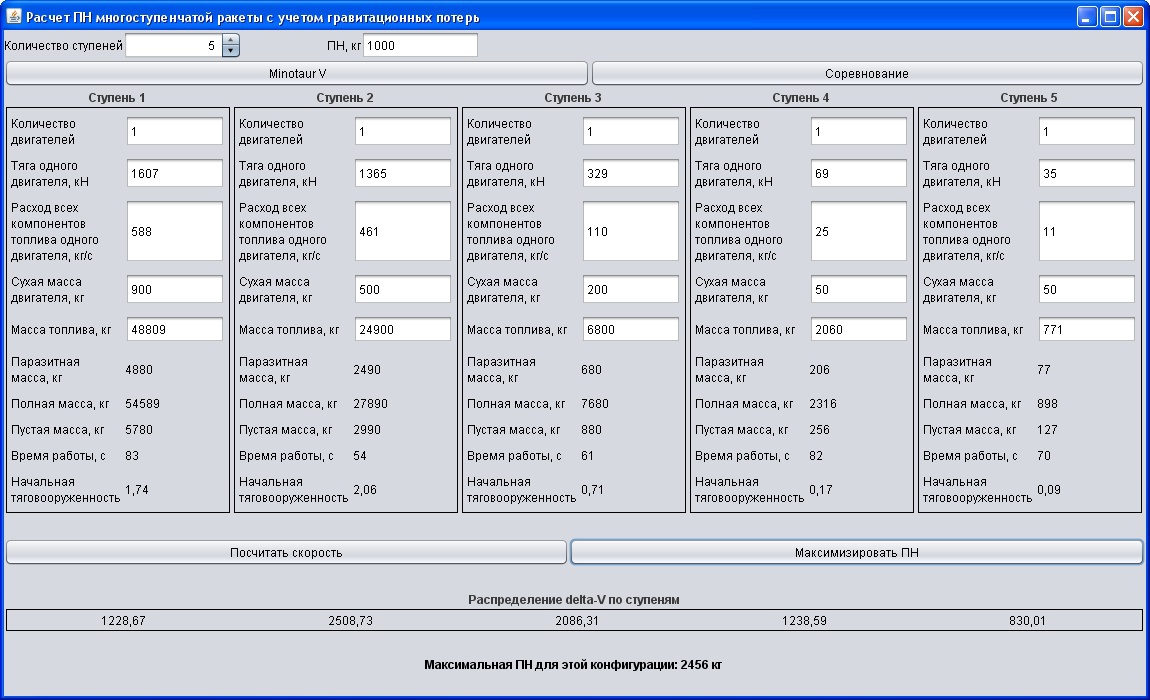
आप मापदंडों के पाठ क्षेत्रों को भरकर, ऊपर से पेलोड में प्रवेश करके और "गणना की गति" बटन पर क्लिक करके किसी दिए गए पेलोड के लिए एक रॉकेट की अंतिम गति की गणना कर सकते हैं।
आप रॉकेट के इन मापदंडों के लिए अधिकतम पेलोड की गणना भी कर सकते हैं, इस मामले में, "पीएन" फ़ील्ड को ध्यान में नहीं रखा गया है।
एक वास्तविक पांच-गति मिनोटौर वी रॉकेट है। मिनोटौर वी बटन इस रॉकेट के समान मापदंडों को लोड करता है ताकि कार्यक्रम कैसे काम करता है इसका एक उदाहरण दिखा सके।
संक्षेप में, यह "सैंडबॉक्स" मोड है जिसमें आप रॉकेट को मनमाने मापदंडों के साथ बना सकते हैं, यह अध्ययन करते हुए कि विभिन्न पैरामीटर रॉकेट की वहन क्षमता को कैसे प्रभावित करते हैं।
प्रतियोगिता
"प्रतियोगिता" बटन दबाकर "प्रतियोगिता" मोड सक्रिय हो गया है। इस मोड में, एक ही प्रतिस्पर्धा की स्थिति के लिए नियंत्रित मापदंडों की संख्या बहुत सीमित है। सभी चरणों में एक ही प्रकार के इंजन हैं (यह स्पष्टता के लिए आवश्यक है, कई चरणों की आवश्यकता है)। आप इंजन की संख्या को नियंत्रित कर सकते हैं। आप चरणों में ईंधन के वितरण और चरणों की संख्या को भी नियंत्रित कर सकते हैं। अधिकतम ईंधन भार 300 टन है। आप कम ईंधन भर सकते हैं।
उद्देश्य : अधिकतम पीएन प्राप्त करने के लिए न्यूनतम संख्या में इंजन का उपयोग करना। यदि बहुत सारे लोग हैं जो खेलना चाहते हैं, तो प्रत्येक संख्या में इंजनों की अपनी स्टैंडिंग होगी।
जो लोग चाहते हैं वे टिप्पणियों में उपयोग किए गए मापदंडों के साथ अपना परिणाम छोड़ सकते हैं। सौभाग्य!
UPD: धन्यवाद
0serg , बेहतर सूत्र।