संख्याओं का समरूपता

संख्याओं का समरूपता
1. परिचय
हमारी दुनिया में, एक-दूसरे के समान, सब कुछ आपस में जुड़ा हुआ है, समान या समान पैरामीटर हैं। अक्सर इन गुणों को समरूपता कहा जाता है। ब्रीफ ऑक्सफोर्ड डिक्शनरी में, समरूपता को "सौंदर्य, शरीर के कुछ हिस्सों की आनुपातिकता या किसी पूर्ण, संतुलन, समानता, सद्भाव, सुसंगतता के कारण" के रूप में परिभाषित किया गया है। [१] बहुत बार, समरूपता स्वयं गणित और भौतिकी में प्रकट होती है। भौतिकी में, समरूपता गुण क्वांटम यांत्रिकी और इसके गणितीय उपकरण में स्पष्ट रूप से प्रकट होते हैं, उदाहरण के लिए, श्रोडिंगर समीकरण [2]। गणित में, एक विशेष गणितीय उपकरण है जो समानता और समरूपता की अवधारणाओं के साथ संचालित होता है। इस गणितीय उपकरण को समूह सिद्धांत [3] कहा जाता है। गणित में समरूपता के व्यावहारिक अनुप्रयोगों में से एक सार्वजनिक कुंजी एन्क्रिप्शन "आरएसए" [4] है।

2. अवशिष्ट प्राइम का मैट्रिक्स

कटौती और तुलना मोडुलो की परिभाषा पर विचार करें। यहाँ आधुनिक व्याख्यात्मक शब्दकोश में दी गई परिभाषा है। संख्या "a" को "बी" मोड्यूलो "मी" का अवशेष कहा जाता है यदि अंतर "ए - बी" "एम" (ए, बी, एम> 0 पूर्णांक हैं) से विभाजित है। यही है, "ए" तुलनीय है "बी" मोडुलो "एम"।

एक mod ​​बी (मॉड एम)

इसका मतलब यह है कि अगर "a" पूरी तरह से "m" से विभाज्य नहीं है, तो "b" "a" को "m" से विभाजित करने के लिए शेष है। दो पूर्णांक "ए" और "बी" तुलनीय मोड्यूलो हैं सकारात्मक पूर्णांक "एम" यदि, "एम" द्वारा विभाजित होने पर, वे एक ही अवशिष्ट देते हैं।
एक प्रमुख पूर्णांक लें और इसे "b" द्वारा निरूपित करें। अंतराल में पूर्णांक का सेट (1,2,3, ... बी -1) "बी" द्वारा दर्शाया गया है। यदि यह सेट एक कॉलम के रूप में लिखा जाता है, तो नीचे से ऊपर तक बढ़ते क्रम में, हमें मैट्रिक्स कॉलम मिलता है। इस कॉलम के सभी नंबर एक के बाद एक व्यवस्थित होते हैं, उनकी संख्या "b - 1" है। इस कॉलम को संख्या "1" से निरूपित करें। सेट "बी" से प्रत्येक संख्या को शेष के साथ "बी" द्वारा विभाजित और विभाजित किया जाएगा। विभाजन से उत्पन्न अवशेष एक कॉलम में लिखे गए हैं। इस कॉलम को "2" नंबर से चिह्नित करें और इसे कॉलम नंबर "1" के दाईं ओर रखें। अवशेषों की व्यवस्था करना आवश्यक है ताकि वे संख्याओं के अनुरूप हों, और उनके साथ एक ही पंक्ति पर हों। उसके बाद, हम "बी" सेट से प्रत्येक संख्या को तीसरी शक्ति तक बढ़ाते हैं और शेष के साथ "बी" से विभाजित करते हैं। प्राप्त अवशेषों से, हम संख्या "3" के नीचे एक स्तंभ बनाते हैं, स्तंभ संख्या "2" के साथ सादृश्य द्वारा। फिर, सादृश्य द्वारा, हम अगली डिग्री तक बढ़ाते हैं और शेष भाग को "b" द्वारा खोजते हैं। हम एक्शन तब तक करते हैं जब तक कि एक्सपोर्टर हम सेट "बी" से संख्याओं का निर्माण "बी" से कम नहीं करता है। नतीजतन, हम आकार (बी -1) एक्स (बी -1) का एक वर्ग मैट्रिक्स प्राप्त करते हैं।

प्राइम पूर्णांक "बी = 23" के लिए इस तरह के एक वर्ग मैट्रिक्स का एक उदाहरण चित्र 1 में प्रस्तुत किया गया है।


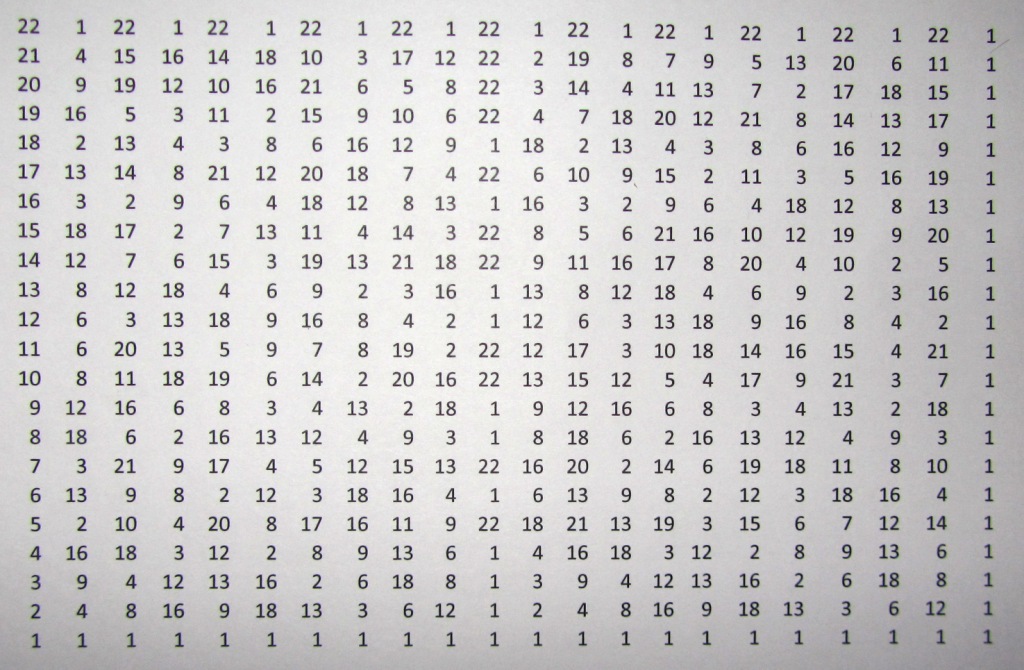
अंजीर। 1 एक प्रमुख पूर्णांक b = 23 के अवशिष्टों का मैट्रिक्स।

परिणामी मैट्रिक्स में अद्भुत गुण हैं:

- यह स्पष्ट रूप से देखा गया है कि मैट्रिक्स के अंतिम कॉलम में एक यूनिट होते हैं। यह पूरी तरह से Fermat की सादगी परीक्षण के अनुरूप है। एक एन -1 n 1 (मॉड एन) [5]।
- यह ध्यान दिया जाना चाहिए कि संख्या के साथ कॉलम (बी -1) / 2 ("बी" माइनस 1 2 से विभाजित) सेट "बी" के केवल दो मान शामिल हैं। ये मान 1 और (b-1) हैं।
- संख्याओं के मान, कॉलम में "बी" सेट करते हैं, अंतराल के मध्य के बारे में सममित हैं, अर्थात मूल्यों की जोड़ी (बी -1) / 2 और (बी + 1) / 2।
- अलग-अलग कॉलम के लिए समरूपता के प्रकार अलग-अलग हैं।
- सम संख्या वाले स्तंभों के लिए, मान अंतराल के मध्य से समान होते हैं, अर्थात। मूल्यों की जोड़ी (बी -1) / 2 और (बी + 1) / 2 संयोग। अंजीर में दिखाए गए मैट्रिक्स के लिए। 1, शेष 11 वर्ग को 23 से विभाजित किया गया और शेष 12 वर्ग को 23 से विभाजित किया गया और 6 के बराबर।
- विषम संख्या वाले स्तंभों के लिए, मान अंतराल के मध्य से समान होते हैं, अर्थात। मूल्यों की जोड़ी (बी -1) / 2 और (बी + 1) / 2, कुल मिलाकर, हमेशा "बी" के बराबर होती हैं। अंजीर में दिखाए गए मैट्रिक्स के लिए। 1, तीसरी डिग्री में 11 का शेष, 23 से विभाजित, 20 है, तीसरी डिग्री में 12 का शेष, 23 से विभाजित है, 3. कुल मिलाकर, ये दो अवशेष 23 हैं, अर्थात्। "बी" के बराबर।

ऊपर वर्णित सभी गुण और अंजीर में दिखाए गए मैट्रिक्स के लिए माना जाता है। 1, अन्य प्रमुख पूर्णांकों के लिए समान नियमों के अनुसार निर्मित मेट्रिक्स में निहित हैं।

3. मिश्रित संख्या के अवशिष्टों का मैट्रिक्स

धारा 2 में माना गया मैट्रिक्स, primes की समरूपता को दर्शाता है। मिश्रित संख्याओं के लिए, समान नियमों द्वारा निर्मित एक मैट्रिक्स काफी भिन्न होता है। यह प्राइम मैट्रिक्स के गुणों को विरासत में मिला है, लेकिन यह नए गुणों को भी प्राप्त करता है। एक कंपाउंड नंबर पर विचार करें, जो दो प्राइम "x" और "y" का उत्पाद है। इसी तरह, संख्या के मूल्य को "बी" द्वारा निरूपित किया जाता है, और अंतराल (1, बी -1) में सभी संख्याओं के सेट को "बी" द्वारा निरूपित किया जाता है। सम्मिश्र संख्या "b = 35" पर विचार करें, जो कि "x = 5" और "y = 7" को गुणा करने का परिणाम है। हम संख्यात्मक अंतराल (35-1) के लिए विभिन्न डिग्री के अवशेषों का एक मैट्रिक्स बनाते हैं। अवशेषों का मैट्रिक्स अंजीर में प्रस्तुत किया गया है। 2


अंजीर। एक मिश्रित संख्या के अवशेषों के 2 मैट्रिक्स b = 35।
कुछ गुण अवशिष्ट primes के मैट्रिक्स से विरासत में मिले हैं। उदाहरण के लिए, स्तंभों में मौजूद संख्याओं के मान संख्यात्मक अंतराल के मानों के मध्य के सममित होते हैं, अर्थात्। मान (बी -1) / 2 और (बी + 1) / 2।

अंजीर में दिखाया गया मैट्रिक्स। 2, नए गुण वहन करती है:

- मैट्रिक्स की पंक्तियों के मूल्य, जिसमें पहले कॉलम में एक समग्र संख्या के विभाजकों के गुणक होते हैं, संख्यात्मक मान लेते हैं जो एक समग्र संख्या के विभाजकों के गुणक होते हैं और कभी भी 1 के बराबर नहीं होते हैं। उदाहरण के लिए, अंजीर के मैट्रिक्स में। 2, पंक्ति 5, दूसरे कॉलम में, मान 25 है, तीसरे 20 में, चौथे 30 में, और इसी तरह। ये सभी मान 5 के कई हैं।
- यदि हम उन पंक्तियों को बाहर करते हैं जिनके मूल्य संख्या "बी" के विभाजकों के गुणक हैं, तो दो कॉलम होना सुनिश्चित है जिसमें शेष मूल्य 1. हैं। उदाहरण के लिए, अंजीर में। 2 संख्या 12, 24 के साथ कॉलम हैं।
- इन दो चयनित कॉलम में, सबसे बड़ा कॉलम नंबर (x-1) (y-1) का उत्पाद है। यानी यदि कारकों में से प्रत्येक 1 को घटाते हैं और उन्हें गुणा करते हैं, तो हमें सबसे बड़े चयनित कॉलम की संख्या मिलती है। अंजीर में मैट्रिक्स के लिए। "बी" संख्या के 2 कारक हैं 5 और 7. यदि आप उनमें से प्रत्येक से 1 घटाते हैं और गुणा करते हैं, तो हमें (5-1) x (7-1) = 24 मिलता है। यह वास्तव में सबसे बड़े चयनित कॉलम की संख्या है। यह ध्यान दिया जाना चाहिए कि इस मामले में, स्तंभ संख्या यूलर फ़ंक्शन के बराबर है, जिसका मान (x-1) x (y-1) = = (n) है। [6]।
- 1 के बराबर चार मान आवश्यक रूप से दूसरे कॉलम में मौजूद हैं। अभाज्य संख्या के अवशिष्टों के मैट्रिक्स के लिए और सेट (B (1, b-1) के बराबर "B" के मान) के लिए, दूसरे कॉलम में मान 1 लेते हैं। एक समग्र संख्या के अवशिष्टों के मैट्रिक्स के लिए, दो और संख्याएँ होती हैं। सेट "बी", जब चुकता और "बी" द्वारा विभाजित किया जाता है, तो शेष 1. 1. अंजीर में होता है। 2 संख्या 6 और 29 हैं।
- हमेशा संख्याओं के जोड़े होते हैं, एक दूसरे का अनुसरण करते हुए "बी" सेट करते हैं, जिनमें से मान "संख्या" बी के भाजक "x" और "y" के गुणक होते हैं। अंजीर में मैट्रिक्स के लिए। 2 जोड़े हैं (14, 15) और (20, 21)।

ऊपर वर्णित सभी गुण और अंजीर में दिखाए गए मैट्रिक्स के लिए माना जाता है। 2, अन्य मिश्रित पूर्णांक के लिए समान नियमों के अनुसार निर्मित मेट्रिक्स में निहित हैं।

4. संख्याओं का गुणन

यदि हम RSA सार्वजनिक कुंजी एन्क्रिप्शन विधि [4] पर विचार करते हैं, तो इसका उपयोग एक संयुक्त संख्या के अवशिष्ट मैट्रिक्स में पारस्परिक रूप से विपरीत मैपिंग के अस्तित्व पर आधारित है। अगर हम समग्र संख्या "b" लेते हैं, तो इसके अवशिष्ट मैट्रिक्स में हमेशा दो कॉलम "c" और "d" मौजूद होते हैं, जिसके लिए निम्न स्थितियाँ सत्य हैं:

(बी 1 ** सी) 1 सी 1 (मॉड बी); (c1 ** d)) d1 (mod b); बी 1 = डी 1

जहाँ b1, c1, d1 कॉलम 1, c, d में संख्यात्मक मान हैं।

यही है, समग्र संख्या "बी" के लिए हमेशा दो नंबर "सी", "डी" रेंज (1, बी -1) से होते हैं, जिसके लिए क्रियाओं का क्रम सत्य है:
- सीमा (1, बी -1) से किसी भी संख्या "बी 1" के शेष भाग को निर्धारित करें "पावर" और "बी" द्वारा विभाजित। इस शेष को "c1" द्वारा निरूपित करें।
- परिणामी शेष "c1" को "d" की शक्ति तक बढ़ाएं और शेष के साथ "b" से विभाजित करें। इस शेष को "d1" द्वारा निरूपित करें।
- परिणामी शेष "d1" हमेशा "b1" के बराबर होता है।
RSA एन्क्रिप्शन एल्गोरिथ्म के लिए, (c, b) सार्वजनिक कुंजी है, (d, b) गुप्त कुंजी है।



अंजीर। 3 एक मिश्रित संख्या के अवशेषों की मैट्रिक्स b = 33।

संख्या बी = 33 के अवशेषों के मैट्रिक्स पर विचार करें, अंजीर। 3. इस संख्या के लिए, सी = 3, डी = 7। हम पहले कॉलम से कोई भी संख्या लेते हैं, उदाहरण के लिए 8 और इसे 3 डिग्री तक बढ़ाएं, शेष 17 है। संख्या 17 को 7 की शक्ति तक उठाया गया है, शेष 8 है, अर्थात्। यह शेष पहले कॉलम से मूल संख्या के बराबर है।
RSA आम सार्वजनिक कुंजी एन्क्रिप्शन एल्गोरिदम में से एक है। एन्क्रिप्शन तरीकों में सुधार के साथ, गुप्त संदेशों को डिक्रिप्ट करने के तरीकों में सुधार हो रहा है।
अक्सर वे आरएसए माथे के लिए डिक्रिप्शन कार्य को हल करने की कोशिश करते हैं, अर्थात। आधार यौगिक संख्या के विभाजक ज्ञात कीजिए। इन विधियों को संख्याओं का कारक कहा जाता है। मूल्यों की सरल गणना और संख्याओं के सत्यापन के अलावा, वे द्विघात चलनी विधि का उपयोग करते हैं।

इस पद्धति का आधार यह है कि संख्या "बी" के वर्ग और भाग से अवशिष्ट के भाग संख्या के पूर्ण वर्ग हैं। अंजीर में। 2 पूर्ण वर्ग पहले कॉलम से संख्याओं (11, 12, 17) के द्विघात अवशेष हैं। संख्या "बी" के विभाजकों को खोजने के लिए, द्विघात शेष से वर्गमूल निकालना आवश्यक है। परिणाम, अर्थात्। वर्गमूल, संख्या "बी" से घटाएं या संख्या "बी" में जोड़ें। "बी" के भाजक के गुणकों को प्राप्त किया जाएगा। यूक्लिडियन एल्गोरिथ्म का उपयोग करते हुए, कोई भी "बी" संख्या के विभाजक पा सकता है।
अंजीर में। 2, संख्या 11 के लिए, द्विघात शेष 16 है। हम 16 से वर्गमूल निकालते हैं, यह 4 है। 11 से हम 4 जोड़ते हैं, हम 15 प्राप्त करते हैं, संख्या 5 का एक गुणक है। 11 से हम 4 घटाते हैं, हमें 7 मिलता है, संख्या विभाजक 7 के बराबर है।

संख्याओं के गुणन के सबसे आधुनिक तरीकों में से एक संख्या क्षेत्र [7] की चलनी विधि है। यह विधि आपको चेक किए गए मानों की संख्या को कम करने और गणनाओं के समय को कम करने की अनुमति देती है। संख्यात्मक क्षेत्र की छलनी विधि और एक समग्र संख्या के अवशिष्ट के मैट्रिक्स के गुणों का उपयोग करके, कोई भी महत्वपूर्ण महत्वपूर्ण परिणाम प्राप्त कर सकता है।

संख्याओं के गुणन के तरीकों के प्रायोगिक सत्यापन के लिए, कोई तथाकथित Mersenne नंबर [8] का उपयोग कर सकता है। ये संख्या "n", शून्य से 1 की शक्ति के लिए नंबर 2 का प्रतिनिधित्व करती है, जहां "n" एक प्राकृतिक संख्या है। केवल Mersenne की संख्या सीमित संख्या में प्रमुख हैं, बाकी विभाजकों की एक सीमित संख्या में विघटित हैं।
एक अच्छे उदाहरण के रूप में, डिविजर्स में से एक, 4099 की डिग्री में 2 नंबर, माइनस 1, के बराबर है -
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717675764345142
549580867720367836084289513946899287311856029114297

4. साहित्य

[१] डी इलियट, पी। डेबर "भौतिकी में समरूपता खंड १ में", एमआईआर पब्लिशिंग हाउस, १ ९ iot३।
[२] "श्रोडिंगर समीकरण", en.wikipedia.org/wiki/ श्रोडिंगर समीकरण।
[३] पी। एस। अलेक्जेंड्रोव, "ग्रुप थ्योरी का परिचय," मास्को विज्ञान, जीआरएफएमएल, 1980।
[४] "आरएसए", en.wikipedia.org/wiki/RSA
[५] "फार्म टेस्ट", en.wikipedia.org/wiki/Test_Farm
[६] "यूलर फंक्शन", http://ru.wikipedia.org/wiki/Euler_Function।
[[] "एक नंबर फील्ड को भेजने के लिए सामान्य तरीका", en.wikipedia.org/wiki/General_Numeric_ Field_Grid_Method।
[[] "मेरसेन नंबर," http://ru.wikipedia.org/wiki/Mersenna_Numbers।