कुछ समय पहले, मैं संख्यात्मक सिमुलेशन के OpenFOAM पुस्तकालय में होने वाले संचालन, प्रक्रियाओं के विवरण की तलाश में था। मुझे परिमित मात्रा पद्धति, शास्त्रीय अंतर योजनाओं और विभिन्न भौतिक समीकरणों के कई सार वर्णन मिले। मैं और अधिक विस्तार से जानना चाहता था - इस तरह के और इस तरह के आउटपुट फ़ाइल में ये मूल्य कहां से आए, fvSchemes, fvSolution कॉन्फ़िगरेशन फ़ाइलों में इन या उन मापदंडों के पीछे क्या भाव हैं?
जो लोग भी रुचि रखते हैं - इस लेख के लिए। जो लोग OpenFOAM से परिचित हैं या इसमें लागू किए गए तरीकों के साथ - पीएम में मिली त्रुटियों और अशुद्धियों के बारे में लिखते हैं।
हब पर OpenFOAM के बारे में पहले से ही कुछ लेख थे:
अभ्यास में OpenFOAMOpenFOAM एक भौतिकी प्रोग्रामर के दृष्टिकोण सेइसलिए, मैं इस तथ्य पर ध्यान नहीं दूंगा कि यह संख्यात्मक सिमुलेशन के लिए एक "खुला (GPL) मंच है, जिसका उद्देश्य परिमित मात्रा विधि द्वारा आंशिक अंतर समीकरणों के समाधान से संबंधित मॉडलिंग के लिए है, और व्यापक रूप से निरंतरता यांत्रिकी की समस्याओं को हल करने के लिए उपयोग किया जाता है"।
आज, एक सरल उदाहरण के साथ, मैं OpenFOAM में गणना के दौरान होने वाले संचालन का वर्णन करूंगा।
तो, ज्यामिति को देखते हुए - 1 मीटर के किनारे वाला घन:
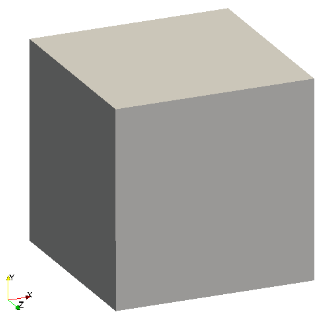
हमें एक निश्चित स्केलर फ़ील्ड (तापमान, मात्रा की मात्रा) के प्रवाह-प्रसार के अनुकरण के कार्य का सामना करना पड़ता है, जो शरीर के वॉल्यूम के अंदर निम्नलिखित परिवहन समीकरण (1) द्वारा दिया गया है।
(1)
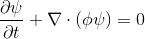
।
जहाँ
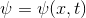
एक अदिश मात्रा, उदाहरण के लिए, तापमान [के] या किसी पदार्थ की सांद्रता को व्यक्त करता है, और

पदार्थ स्थानांतरण, द्रव्यमान प्रवाह [किग्रा / एस] व्यक्त करता है।
उदाहरण के लिए, इस समीकरण का उपयोग गर्मी वितरण के मॉडल के लिए किया जाता है
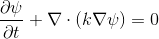
।
जहां k तापीय चालकता है, और
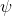
- तापमान [के]।
विचलन ऑपरेटर वास्तव में हैऑपरेटर
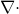
।
आपको याद दिला दूं कि एक नबला ऑपरेटर (हैमिल्टन ऑपरेटर) है, जो इस प्रकार लिखा जाता है:

।
जहाँ मैं, j, k यूनिट वैक्टर हैं।
यदि हम एक वेक्टर मात्रा द्वारा नबल ऑपरेटर को मापते हैं, तो हमें इस वेक्टर का विचलन होता है:
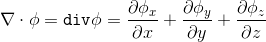
"भौतिकी के दृष्टिकोण से, वेक्टर क्षेत्र का विचलन इस बात का सूचक है कि अंतरिक्ष में दिया गया बिंदु इस क्षेत्र का स्रोत या सिंक है"
यदि हम एक स्केलर द्वारा नाबला ऑपरेटर को गुणा करते हैं, तो हमें इस स्केलर का ग्रेडिएंट मिलता है:
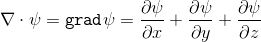
ढाल स्केलर मान के किसी भी दिशा में वृद्धि या कमी को दर्शाता है।

।
समस्या की सीमा की स्थिति निम्नानुसार है: एक चेहरे में है, चेहरा-बाहर, दूसरे चेहरे चिकनी दीवारें हैं।

घन की मात्रा को परिमित मात्राओं में विभाजित करना
हमारी ग्रिड बहुत सरल होगी - क्यू अक्ष को Z अक्ष के साथ 5 समान कोशिकाओं में विभाजित करें।

कई सूत्र
परिमित मात्रा विधि यह प्रदान करती है कि (1) अभिन्न रूप में (2) प्रत्येक अंतिम मात्रा के लिए किया जाएगा
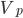
।
(2)
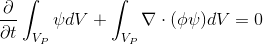
।
जहाँ
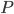
परिमित मात्रा का ज्यामितीय केंद्र है।
सरल बनाने के लिए, हम अभिव्यक्ति के पहले शब्द (2) को इस प्रकार रूपांतरित करते हैं:
(2.1) (HJ-3.12) *

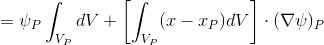
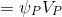
जैसा कि देखा जा सकता है, हमने स्वीकार किया कि स्केलर की मात्रा अंतिम मात्रा और मान के भीतर रैखिक रूप से भिन्न होती है

कुछ बिंदु पर

अंतिम मात्रा के अंदर गणना की जा सकती है:
(2.2)

।
जहाँ

अभिव्यक्ति के दूसरे कार्यकाल को सरल बनाने के लिए (2), हम सामान्यीकृत
गॉस-ओस्ट्रोग्राडस्की प्रमेय का उपयोग करते हैं: एक वेक्टर क्षेत्र के विचलन का अभिन्न अंग

मात्रा द्वारा
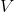
सतह के माध्यम से वेक्टर के प्रवाह के बराबर है
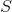
, इस मात्रा को सीमित करना। मानव भाषा में, "एक परिमित मात्रा से सभी प्रवाह का योग इस मात्रा के चेहरे के माध्यम से प्रवाह के योग के बराबर है:"
(2.3)
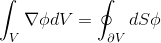
।
जहाँ

बंद सतह सीमित मात्रा
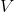
।
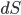
- एक वेक्टर सामान्य मात्रा के लिए निर्देशित

।
यह देखते हुए कि परिमित मात्रा समतल चेहरों के एक समूह द्वारा सीमित है, अभिव्यक्ति (2.3) को सतह पर अभिन्न के योग में परिवर्तित किया जा सकता है:
(2.4) (HJ-3.13)
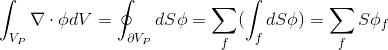
।
जहाँ

चेहरे के केंद्र में चर के मूल्य को व्यक्त करता है,
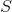
- क्षेत्र वेक्टर, चेहरे के केंद्र को छोड़ देता है, सेल से दूर (स्थानीय रूप से), सेल से कम इंडेक्स के साथ सेल से दूर (उच्च वैश्विक रूप से) के साथ निर्देशित किया जाता है।
वेक्टर एस के बारे में थोड़ा और
आदेश में एक ही वेक्टर मापदंडों को स्टोर करने के लिए नहीं
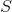
दो बार से यह स्पष्ट है कि दो पड़ोसी कोशिकाओं में, कोशिकाओं के बीच की सीमा के लिए सामान्य वेक्टर, सेल के केंद्र से दूर निर्देशित केवल दिशा-संकेत में भिन्न होगा। इसलिए, चेहरे और सेल के बीच एक मालिक-पड़ोसी संबंध बनाया गया था। यदि वर्ग वेक्टर
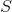
(कम सूचकांक वाले सेल से वैश्विक, सकारात्मक दिशा एक उच्च सूचकांक वाले सेल से) केंद्र से FROM इंगित करता है
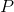
सेल सेल और वेक्टर के बीच का संबंध है
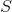
, या बल्कि, सेल और चेहरे के बीच, मालिक द्वारा निरूपित)। मामले में इस वेक्टर
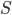
प्रश्न में सेल के अंदर बिंदु, तो संबंध पड़ोसी है। दिशा परिमाण (+ मालिक के लिए और - पड़ोसी के लिए) के संकेत को प्रभावित करती है और इसे जोड़ते समय महत्वपूर्ण है, नीचे देखें।

(HJ-3.16)
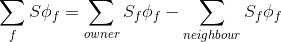
अंतर योजनाओं के बारे में
मूल्य

चेहरे के केंद्र में मूल्यों के माध्यम से गणना की जाती है

आसन्न कोशिकाओं के केंद्रों में - ऐसी अभिव्यक्ति की विधि को अंतर योजना कहा जाता है। OpenFOAM में, अंतर योजना का प्रकार फ़ाइल
/ सिस्टम / fvSchemes में निर्दिष्ट है:
divSchemes { default none; div(phi,psi) Gauss linear; }
गॉस - का मतलब है कि केंद्रीय अंतर योजना का चयन किया जाता है;
रैखिक - का मतलब है कि कोशिकाओं के केंद्रों से चेहरे के केंद्रों तक प्रक्षेप रैखिक रूप से घटित होगा।

मान लीजिए कि हमारा स्केलर मान एक केंद्र से रैखिक रूप से परिमित मात्रा के भीतर भिन्न होता है। फिर चेहरे के केंद्र में अनुमानित मूल्य की गणना सूत्र के अनुसार की जाएगी:
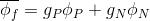
वजन कहां हैं
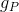
और
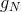
के रूप में गणना की
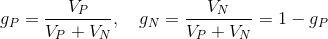
जहाँ
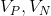
- सेल वॉल्यूम।
बेवल किए गए कोशिकाओं के मामलों के लिए, अनुमानित वजन की गणना के लिए अधिक जटिल सूत्र हैं।
इस प्रकार, सेल चेहरों के केंद्रों में phi_f मानों की गणना कोशिकाओं के केंद्रों में मूल्यों के आधार पर की जाती है। ग्रैडिएंट वैल्यू ग्रेड (phi) की गणना phi_f मान के आधार पर की जाती है।
और इस पूरे एल्गोरिथ्म को निम्नलिखित स्यूडोकोड के रूप में दर्शाया जा सकता है।
1. , 2. ( ) > flux_f = phi_f*S_f. phi_f phi > flux_f -owner -flux_f -neighbour 3. > flux_f = phi_f*S_f > flux_f -owner (neighbour- ) 4. > -
समय का नमूना
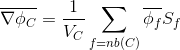
दिया (२.१) और (२.४), अभिव्यक्ति (२) रूप लेता है:
(3)
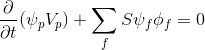
परिमित मात्रा विधि के अनुसार, समय नमूना प्रदर्शन किया जाता है और अभिव्यक्ति (3) के रूप में लिखा जाता है:
(4)
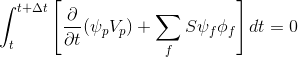
एकीकृत (4):
(4.1)
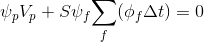
बाएं और दाएं पक्षों को विभाजित करें

:
(5)
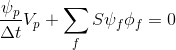
नमूना मैट्रिक्स के लिए डेटा
अब हम प्रत्येक परिमित मात्रा के लिए रैखिक समीकरणों की एक प्रणाली प्राप्त कर सकते हैं
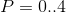
।
नीचे ग्रिड नोड्स की संख्या है जो हम उपयोग करेंगे।

नोड निर्देशांक / स्थिर / पॉलीमेश / अंक में संग्रहीत हैं 24 ( (0 0 0) (1 0 0) (0 1 0) (1 1 0) (0 0 0.2) (1 0 0.2) (0 1 0.2) (1 1 0.2) (0 0 0.4) (1 0 0.4) (0 1 0.4) (1 1 0.4) (0 0 0.6) (1 0 0.6) (0 1 0.6) (1 1 0.6) (0 0 0.8) (1 0 0.8) (0 1 0.8) (1 1 0.8) (0 0 1) (1 0 1) (0 1 1) (1 1 1) )
कोशिकाओं के नोड-केंद्रों की संख्या (50, 51 - सीमा के चेहरे के केंद्र):

चेहरों के नोड केंद्रों की संख्या:

तत्वों की मात्रा:
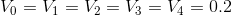
सेल चेहरे पर मूल्यों की गणना करने के लिए इंटरपोलेशन गुणांक की आवश्यकता होती है। सूचकांक "ई" का अर्थ "सेल के दाईं ओर" है। दृश्य के सापेक्ष सही, जैसा कि "कोशिकाओं के नोड-केंद्रों की संख्या" में है:
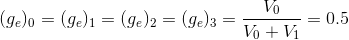
एक नमूना मैट्रिक्स का गठन
पी = 0 के लिए।मात्रा के व्यवहार का वर्णन अभिव्यक्ति (5)
रेखीय बीजीय समीकरणों की एक प्रणाली में बदल जाएगा, जिनमें से प्रत्येक फार्म का है:
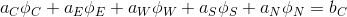
या, चेहरों पर अंकों के सूचकांकों के अनुसार
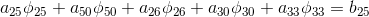
और सेल से / से सभी प्रवाह भी योग के रूप में व्यक्त किए जा सकते हैं
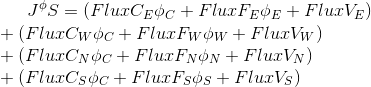
उदाहरण के लिए
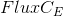
सेल E के केंद्र बिंदु पर प्रवाह का रैखिककरण गुणांक है,
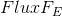
क्या चेहरे के बिंदु-केंद्र पर प्रवाह का रैखिककरण गुणांक है,
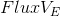
- नॉनलाइनियर भाग (उदाहरण के लिए, स्थिर)।
चेहरों की संख्या के अनुसार, अभिव्यक्ति का रूप होगा:
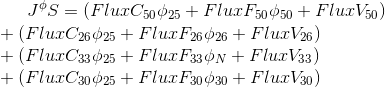
तत्व P_0 के लिए सीमा स्थितियों को देखते हुए, रैखिक बीजगणितीय समीकरण को इस रूप में दर्शाया जा सकता है
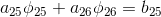
... पहले प्राप्त गुणांक के विकल्प ...
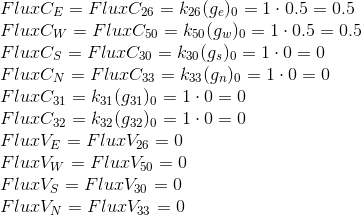
इनलेट से धारा सेल को निर्देशित की जाती है, इसलिए इसका एक नकारात्मक संकेत है।
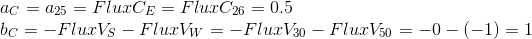
चूंकि हमारी नियंत्रण अभिव्यक्ति में, प्रसार शब्द के अलावा, एक समय अवधि भी है, अंतिम समीकरण जैसा दिखता है
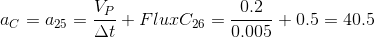
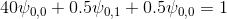 पी = 1 के लिए।
पी = 1 के लिए।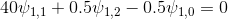 पी = 4 के लिए।
पी = 4 के लिए।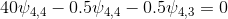
रैखिक बीजगणितीय समीकरणों (SLAE) की प्रणाली को मैट्रिक्स रूप में दर्शाया जा सकता है
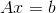
।
जहाँ
=== A(i,j) === 40.5 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40.5
=== b(i,j) === 1 0 0 0 0
अगला, प्राप्त SLAE
fvSchemes में निर्दिष्ट सॉल्वर द्वारा हल किया जाता है।
और परिणाम मूल्यों का एक सदिश है
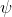
psi = dimensions [0 0 0 0 0 0 0]; internalField nonuniform List<scalar> 5(0.0246875 0.000308546 3.85622e-06 4.81954e-08 5.95005e-10);
जिसके आधार पर वेक्टर के लिए मान प्राप्त किए जाते हैं
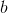
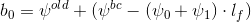
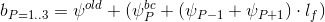

फिर वेक्टर
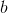
SLAU में प्रतिस्थापित
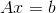
और वेक्टर गणना का एक नया पुनरावृत्ति
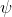
।
और इसलिए जब तक अवशिष्ट आवश्यक सीमा तक नहीं पहुंच जाता।
संदर्भ
* इस लेख में कुछ समीकरणों को यास्क ह्रीवो (HJ समीकरण संख्या है) के शोध प्रबंध से लिया गया है और यदि कोई उनके बारे में अधिक पढ़ना चाहता है (
http://powerlab.fsb.hr/ped/kturbo/OfFOAM/docs/HrvojeJasakPhD.pdf )
यहाँ कार्य फ़ाइलें डाउनलोड करें:
github.com/j-avdeev/caseसॉल्वर फ़ाइलें:
github.com/j-avdeev/matrHyper1Foamएक बोनस के रूप में - एकाग्रता का वितरण कैसे किया जाता है, इसका एक वीडियो
।