19 अप्रैल को होने वाले रूसी कोड कप के पहले क्वालीफिकेशन राउंड की प्रत्याशा में, हमने आपको चैंपियनशिप के इतिहास की सात सबसे दिलचस्प आरसीसी समस्याओं के बारे में बताने का फैसला किया, जो कि ITMO कंप्यूटर प्रौद्योगिकी विभाग की एसोसिएट प्रोफेसर, शिक्षा के क्षेत्र में राष्ट्रपति पुरस्कार के विजेता, आंद्रेई स्टैन्केविच के अनुसार। ACM-ICPC संस्थापक पुरस्कार, आईबीएम विशेष कोचिंग पुरस्कार के विजेता।
हम आपको याद दिलाते हैं कि रूसी कोड कप में भाग लेने के लिए, आपको वेबसाइट
http://russiancodecup.ru/ पर पंजीकरण करने की आवश्यकता है (तीसरे योग्यता दौर की शुरुआत से पहले पंजीकरण खुला होगा)।
2011 फाइनल राउंड, "बी" उलटा कछुआ समस्या
2011 फाइनल राउंड, "डी" अभिलेखागार
2012 द्वितीय योग्यता दौर, "सी" Tetrahedron
2012 क्वालिफाइंग राउंड, "एफ" प्रिंस
2012 फाइनल राउंड, "ई" शफ़ल डेक
2013 क्वालिफाइंग राउंड, "ई" लेजर
2013 फाइनल राउंड, "डी" रोबोट
1) 2011, अंतिम दौर, "बी"
उलटा कछुआ समस्यापार्स:इस समस्या में, किसी दिए गए नंबर k के लिए, एक भूलभुलैया का निर्माण करना आवश्यक था जिसमें ऊपरी बाएं से निचले दाएं सेल तक के मार्ग k के बराबर होंगे, बशर्ते कि इसे केवल दाएं और नीचे जाने की अनुमति हो।
निम्नलिखित पर ध्यान दें। मान लें कि हमारे पास दो लेबिरिंथ हैं जिनमें ऊपरी बाएँ से निचले दाएं कोशिकाओं तक पहुंचने के तरीकों की संख्या क्रमशः एक और बी है।
फिर, उन्हें समानांतर में रखकर, जैसा कि चित्र में दिखाया गया है, हम एक भूलभुलैया प्राप्त कर सकते हैं, जिसके लिए ऊपरी बाएँ से निचले दाएं कक्ष तक जाने के लिए + b रास्ते हैं। और उन्हें क्रमबद्ध रूप से रखते हुए - एक भूलभुलैया प्राप्त करें जिसमें ab पथ हैं।
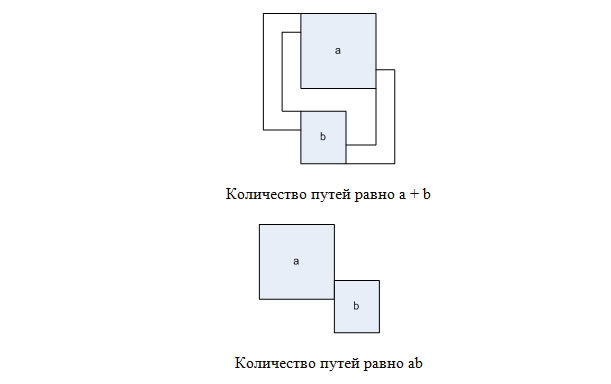
ध्यान दें कि खाली 2 × 2 भूलभुलैया में दो रास्ते हैं, और 1 × 1 भूलभुलैया में एक पथ। इसलिए, संख्या k को एक बाइनरी नंबर सिस्टम में विस्तारित करके और वर्णित विधि का उपयोग करके, हम ऊपरी बाएं से निचले दाएं सेल के लिए कश्मीर पथ के साथ एक भूलभुलैया प्राप्त कर सकते हैं।
K = 19 के लिए इस तरह के भूलभुलैया का एक उदाहरण चित्र में दिखाया गया है।
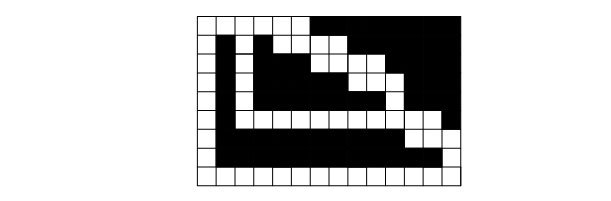
ध्यान दें कि संख्या k के प्रत्येक निर्वहन के लिए, 5 कोशिकाओं को क्षैतिज रूप से आवश्यक है, और 2
60 > 10
18 इसलिए, उपरोक्त योजना आपको 300 × 300 से अधिक के आकार के साथ एक भूलभुलैया बनाने की अनुमति देती है, जो समस्या की स्थिति में आवश्यक है।
2) 2011, फाइनल राउंड, "डी"
अभिलेखागारपार्स:इस कार्य के लिए कम से कम दो अलग-अलग दृष्टिकोण संभव हैं: गतिशील प्रोग्रामिंग या एक लालची एल्गोरिथ्म।
एक अनुक्रम को एक पेड़ के रूप में संग्रहीत करने की प्रक्रिया की कल्पना करें: मध्यवर्ती दृश्यों में से प्रत्येक का प्रत्येक प्रतीक पेड़ के शीर्ष होगा, शीर्ष के बच्चे दो वर्ण होंगे जो दिए गए एक में संग्रह के दौरान "सरेस से जोड़ा हुआ" हैं। प्रारंभिक संख्या पत्तियों में लिखी जाती है, और कार्य सभी मध्यवर्ती कोने के लिए संख्याएं लिखना है, जबकि संग्रह के लिए दंड वर्टिकल की संख्या के बराबर है, जिसके लिए बच्चों में विभिन्न संख्याएं लिखी जाती हैं।
डायनेमिक प्रोग्रामिंग का उपयोग करते हुए समाधान इस प्रकार है: प्रत्येक शीर्ष पर यू हम सबटाइटल के लिए न्यूनतम कुल पेनल्टी पी [यू] [x] जमा करेंगे यदि हम इस शीर्ष पर संख्या x लिखते हैं। ध्यान दें कि शीर्ष पर यह केवल उस संख्या को लिखने के लिए सार्थक है जो सबट्री में पत्तियों में से किसी एक में होती है, इसलिए कुल विकल्पों की संख्या जिस पर विचार किया जाना चाहिए वह है ओ (एन लॉग एन)।
पुनर्गणना निम्न प्रकार से की जाती है: बच्चों और v के साथ शीर्ष u पर विचार करें। मान लीजिए, हमारे पास x का मान लिखने की योजना है। यदि दोनों p [v] [x] और p [w] [x] परिभाषित हैं, तो x को u में रखने के विकल्पों में से एक दोनों बच्चों में x लगाना है, इस विकल्प की कीमत p [v] [x] + p [w है ] [x]। केवल एक बच्चे में एक्स लगाने का विकल्प भी है। मान लीजिए कि हमने x को v में रखने की योजना बनाई है, तो इस विकल्प की लागत p [v] [x] + minp [w] + 1 है, जहां minp [w] सभी y के लिए p [w] [y] का न्यूनतम मूल्य है।
डीपी का उपयोग करके हल करने का एक विकल्प एक लालची समाधान है: प्रत्येक शीर्ष के लिए हम सभी संभावित मूल्यों की एक सूची रखेंगे, उनमें से एक को शीर्ष पर रखकर, हम सबट्री में न्यूनतम जुर्माना प्राप्त करेंगे। यह पता चला है कि एक शीर्ष के लिए इष्टतम सेट खोजने के लिए, यह अपने बच्चों में केवल इष्टतम मूल्यों को रखने की कोशिश करने के लिए पर्याप्त है। इसके अलावा, यदि बच्चों के लिए इष्टतम मूल्यों की सूची में अंतर है, तो आपको इनमें से किसी एक संख्या को लेना होगा। यदि वे नहीं काटते हैं, तो बच्चों में से प्रत्येक का कोई भी मतलब होगा।
हम एक अभ्यास के रूप में प्रस्तुत एल्गोरिथ्म की शुद्धता का प्रमाण छोड़ देंगे।
3) 2012, द्वितीय योग्यता दौर, "सी"
Tetrahedronपार्स:आपको याद दिला दूं कि एक tetrahedron एक पॉलीहेड्रॉन है जिसके चेहरे चार त्रिकोण हैं (दूसरे शब्दों में, एक त्रिकोणीय पिरामिड)।
यह सब इस तथ्य से शुरू होता है कि हम टेट्राहेड्रोन के किनारों के संभावित मैचों को सुलझाते हैं। हम एबीसीडी के रूप में वांछित टेट्राहेड्रोन को दर्शाते हैं। उसकी छह पसलियाँ हैं: AB, AC, AD, BC, BD और CD। सभी 6 से अधिक चलते हैं! = 720 विकल्प, जो मैच किस किनारे से मेल खाता है। अब यह सत्यापित करना बाकी है कि संबंधित टेट्राहेड्रॉन मौजूद है।
टेट्राहेड्रोन के अस्तित्व की जांच कैसे करें? यहां कम से कम तीन समाधान हैं।
पहला समाधान टेट्राहेड्रोन की मात्रा की गणना पर आधारित है। सरलतम उपाय यह है कि टेट्राहेड्रोन की मात्रा की गणना उसके चेहरे द्वारा की जाए। यह कार्य अपने आप में आसान नहीं है, मैं यहाँ सूत्र दूंगा:
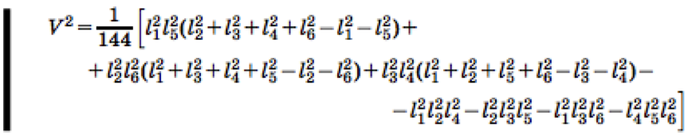
तदनुसार, यदि समानता का दाहिना हाथ नकारात्मक हो जाता है या चेहरे (त्रिकोण असमानता) में त्रिकोण का निर्माण करना असंभव है, तो टेट्राहेड्रॉन अभिसरण नहीं करेगा।
रुचि रखने वालों के लिए
, यह सूत्र यहां प्रदर्शित है ।
समस्या को हल करने के लिए दूसरा दृष्टिकोण ज्यामितीय है। सबसे पहले, सुनिश्चित करें कि एबीसी और बीसीडी मौजूद हैं। अब टेट्राहेड्रॉन बनाने की कोशिश करें। यह स्पष्ट है कि त्रि-आयामी आकृति का निर्माण करते समय, एक समस्या केवल आखिरी छोर के साथ उत्पन्न हो सकती है - यह या तो बहुत लंबा या बहुत छोटा हो सकता है। इसलिए, इस समाधान में, अंतिम रिब की लंबाई सीमा को खोजने का प्रस्ताव है।
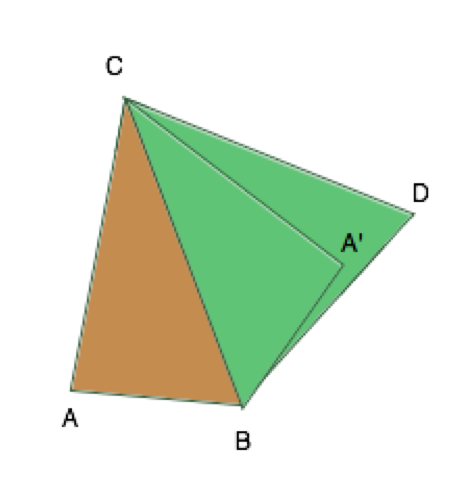
चेहरे रखने के लिए दो सीमित विकल्प हैं, जिसमें टेट्राहेड्रॉन एक सपाट आकृति में बदल जाता है। पहला - जब चेहरों को एक-दूसरे (सीएबी और सीबीडी) के सापेक्ष 180 डिग्री घुमाया जाता है, और दूसरा - जब वे "मुड़े हुए" होते हैं और एक "शून्य कोण" (सीएडीडी और सीडीबी) बनाते हैं। एक दूसरे के सापेक्ष चेहरे की सभी अनुमेय स्थिति इन सीमा के बीच की सीमा में हैं। अंतिम छोर (AD) पहले सीमित संस्करण (AD) में अपनी सबसे बड़ी लंबाई तक पहुँचता है, और अंतिम (A'D) में सबसे छोटा होता है। नतीजतन, एक टेट्राहेड्रॉन मौजूद होगा यदि अंतिम किनारे की यह लंबाई हमारे द्वारा पाई गई सीमा (ए डी डी से एडी) में फिट होती है।
अंक ए और डी और ए 'और डी के बीच की दूरी का पता लगाने के लिए, हम पहले उनके निर्देशांक पाते हैं, त्रिकोण के लिए एक कोने में से एक के लिए आम लेते हैं, और अपने शीर्ष से निकलने वाले किनारों में से एक के माध्यम से एब्सिस्सा अक्ष खींचते हैं। इस निर्देशांक प्रणाली में अन्य सभी कोने के निर्देशांक खोजना काफी सरल है: कोण के पहलू अनुपात और कोसाइन के माध्यम से, हम ध्रुवीय निर्देशांक (कोण, दूरी) में कोने की स्थिति निर्धारित करते हैं, और फिर उन्हें कार्टेशियन समन्वय प्रणाली में अनुवाद करते हैं। कोने के निर्देशांक को जानने के बाद, असंबद्ध कोने के बीच अधिकतम और न्यूनतम दूरी की गणना करना बहुत सरल है।
कार्यक्रम की जांच करनी चाहिए कि शेष चेहरे की लंबाई निर्दिष्ट सीमाओं में फिट होती है या नहीं। यदि ऐसा है, तो ऐसी लंबाई के एक टेट्राहेड्रॉन को "इकट्ठा" किया जा सकता है।
 तीसरी विधि भी ज्यामितीय है।
तीसरी विधि भी ज्यामितीय है। पहले आपको संकेतित पक्षों के साथ सभी त्रिकोणों के अस्तित्व की जांच करने की आवश्यकता है। यदि पक्षों के संकेतित मानों के अनुसार कम से कम एक त्रिभुज का निर्माण नहीं किया जा सकता है, तो टेट्राहेड्रॉन का निर्माण नहीं किया जा सकता है। जांच करने के लिए, गैर-पतित त्रिकोण की असमानता की जांच करना आवश्यक है: इसके किसी भी पक्ष को अन्य दो के योग से कड़ाई से कम होना चाहिए।
कई मामलों में, समाधान केवल इस तक सीमित था; इस बीच, ऐसी स्थितियां हैं जब संकेतित पक्षों के साथ त्रिकोण का निर्माण किया जा सकता है, और उनके लिए एक टेट्राहेड्रोन को इकट्ठा करना असंभव है।
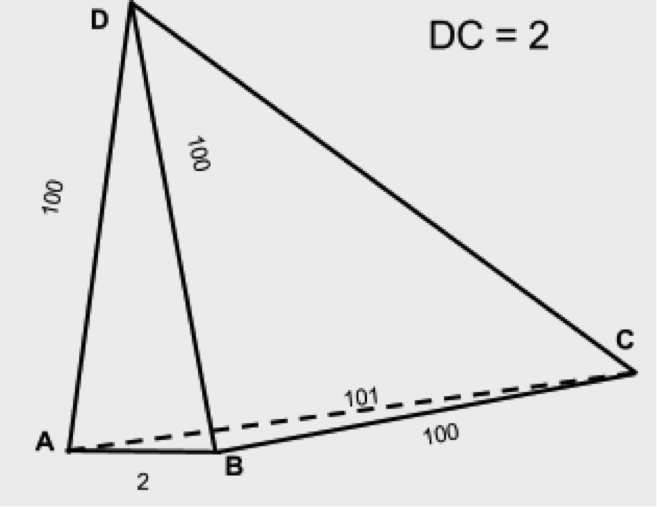
उदाहरण के लिए, यदि हमारे पास चेहरे (100,100,2,101,100,2) हैं, तो त्रिकोण (100,100,2) और (101,100,2) त्रिकोण की असमानता को औपचारिक रूप से संतुष्ट करते हैं, लेकिन ऐसे त्रिकोणों से एक टेट्राह्रोन को जोड़ना असंभव है। आंकड़े से, हम देखते हैं कि एज एसी लगभग एबी के समानांतर है, जिसका अर्थ है कि डी से सी तक की दूरी एबी के सापेक्ष एबीडी के किसी भी झुकाव के लिए शायद ही बदल जाएगी, जिससे हम यह निष्कर्ष निकाल सकते हैं कि डीबी लगभग बीसी के लंबवत है। इस स्थिति में, डीसी को लगभग पैरों के वर्गों के योग की जड़ के रूप में अनुमानित किया जा सकता है, अर्थात, डीसी लगभग 10 होना चाहिए, और 2 बिल्कुल नहीं, जैसा कि हमने स्थिति में मान लिया था।
इसलिए, चेहरों में त्रिकोणों के लिए जाँच के अलावा, त्रिकोणीय कोणों के लिए एक अतिरिक्त परीक्षण करना आवश्यक है। त्रिवेणी कोण के अस्तित्व के लिए दो आवश्यक और पर्याप्त शर्तें हैं:
- त्रिभुज कोण के सपाट कोणों का योग 360 डिग्री से कम होना चाहिए,
- त्रिक कोण के प्रत्येक विमान कोण दो अन्य विमान कोणों के योग से कम होना चाहिए।
समतल कोण त्रिभुज के लिए कोसाइन प्रमेय के माध्यम से पाया जाता है।
कुल मिलाकर, 1088 फैसलों की जाँच करने का लक्ष्य था, जिनमें से केवल 74 (7%) सही थे। 8% रूसी कोड कप QR2 प्रतिभागियों ने इस कार्य को पूरा किया। पहला निर्णय दौर की शुरुआत के 30 मिनट बाद एविक्टॉर उपनाम वाले प्रतिभागी से आया।
4) 2012 क्वालिफाइंग राउंड, "एफ"
प्रिंसपार्स:इस कार्य में, न्यूनतम समय का पता लगाना आवश्यक है जिसके लिए राजकुमार किसी भी जाल में पड़ने के बिना एक आयामी गलियारे के माध्यम से राजकुमारी को गिर जाएगा। ज्ञात कार्यक्रम, आकार और जाल की उपस्थिति / गायब होने का स्थान, साथ ही साथ राजकुमार की गति की गति। चूंकि गलियारा एक-आयामी है, राजकुमार या तो राजकुमारी की ओर बढ़ सकता है, या उससे दूर जा सकता है, या बिल्कुल भी नहीं जा सकता है। जाहिर है, ऐसी परिस्थितियां हैं जब कोई रास्ता नहीं है, और राजकुमार राजकुमारी को नहीं मिलता है - इस मामले में, आपको असंभव को वापस लेने की आवश्यकता है।
इस समस्या का समाधान एक विमान पर जाल का चित्रण करके शुरू करना है जहां x निर्देशांक गलियारे में स्थिति है और y समन्वय समय है। अब इस विमान के संदर्भ में समस्या का सुधार किया जा सकता है: इसे न्यूनतम y के साथ बिंदु (0, 0) से बिंदु (x, y) तक प्राप्त करना आवश्यक है, जबकि इसे लंबवत रूप से ऊपर (अभी भी खड़े होने के लिए), तिरछे दाएं और ऊपर बाएं जाने की अनुमति है (चाल गलियारे के साथ) और कुछ आयतों (जाल) में प्रवेश करने की मनाही है। इसे आयत की सीमा पर होने की अनुमति है।
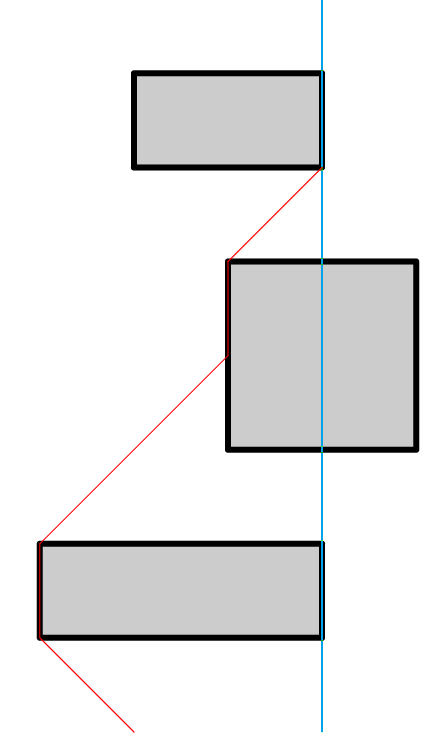
इस तरह के कार्य में इष्टतम पथ में कई समान भाग शामिल होंगे, जिनमें से प्रत्येक में आयतों में से एक की सीमा के अनुरूप समन्वय करने के लिए विकर्णों में से एक के साथ आंदोलन शामिल होगा, इसके बाद ऊर्ध्वाधर आयताकार आंदोलन इस आयत के ऊपरी कोने तक। इस प्रकार, मुख्य बिंदु प्रत्येक आयत के ऊपरी बाएं और ऊपरी दाएं कोने हैं और आपको उनके बारे में पता लगाने की आवश्यकता है कि क्या वहां पहुंचना संभव है।
तिरछे चलते समय, हम वर्तमान स्थिति के ऊपर स्थित कई आयतों का समर्थन करेंगे। चूंकि यह आयतों की सीमा पर होना संभव है, तो वर्तमान "गलियारे" समन्वय पर शुरू या समाप्त होने वाले आयतों को ध्यान में नहीं लिया जाएगा। निचले किनारे पर व्यवस्थित एक सेट में आयतों को संग्रहीत किया जाएगा। इस तरह के सेट को एक स्लाइस कहा जाएगा। सेट को संग्रहीत करने के लिए, आप डेटा संरचनाओं का उपयोग कर सकते हैं जैसे लाल-काले या कार्टेशियन पेड़ या प्राथमिकता कतार। निचले आयत के निचले किनारे को स्लाइस के किनारे कहा जाएगा। यदि स्लाइस में आयताकार नहीं होते हैं, तो हम इसके किनारे को अनंत मानते हैं।
चूंकि समय किसी भी आंदोलन के साथ समन्वय बढ़ता है, हम इस समन्वय के गैर-घटते क्रम में आयतों के कोणों पर विचार करेंगे। अगले कोण पर विचार करते हुए, हम इसे दोनों दिशाओं में तिरछे तरीके से स्थानांतरित करने का प्रयास करेंगे। आयतों की सीमाओं के अनुरूप निर्देशांक पर आंदोलन किया जाता है। अगले समन्वय तक पहुंचते हुए, हम जाँचते हैं कि क्या यह संभव है, एक आयत के संगत ऊपरी कोने में जाने के लिए, ऊपर की ओर बढ़ रहा है। यदि यह कोण वर्तमान स्लाइस के किनारे से अधिक नहीं है, तो एक कोण तक पहुंचा जा सकता है। यह भी जांचना आवश्यक है कि आंदोलन इस समन्वय में शुरू होने वाले आयतों में से एक के किनारे पर आराम नहीं करता है। यदि आप दरवाजे के समन्वय एक्स तक पहुंचने में कामयाब रहे, तो आपको वर्तमान उत्तर को अपडेट करने की आवश्यकता है। यदि, जब एक समन्वय से दूसरे में जाता है, तो कट का किनारा पार हो गया था, फिर संक्रमण के दौरान आयत के निचले किनारे तक पहुंच गया था, और आंदोलन को रोकना होगा।
एक-एक करके सभी कोनों की जांच की और उनमें से प्रत्येक के दोनों किनारों पर कदम रखते हुए, हम न्यूनतम संभव उत्तर या जानकारी पाएंगे कि दरवाजा उपलब्ध नहीं है। वर्णित एल्गोरिदम ओ (एन 2 लॉग एन) संचालन करता है, क्योंकि विभिन्न निर्देशांक के विकर्ण ओ (एन) के साथ ओ (एन) कोणों में से प्रत्येक से जाना आवश्यक है और ओ (एन) आयतों की जांच करें। इसके अलावा, प्रत्येक कोण के लिए स्लाइस को बनाए रखने के लिए ओ (एन लॉग एन) संचालन करना आवश्यक है, क्योंकि स्लाइस से ओ (एन) आयतों को जोड़ना और निकालना आवश्यक है।
आयतों को पारित करने के लिए निम्नलिखित संभव विकल्प हैं जिन्हें आपको प्रक्रिया के लिए याद रखना चाहिए।
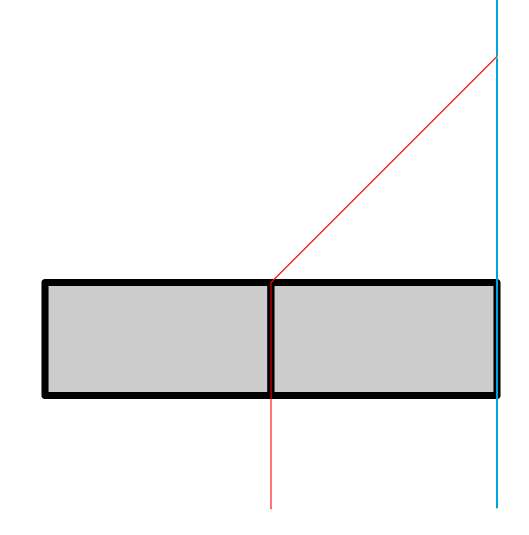
और
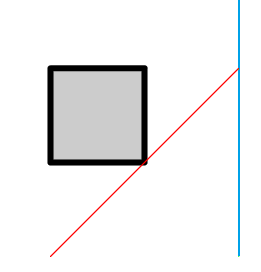
उसी समय, अगले परीक्षण में दरवाजे को पकड़ना असंभव है।
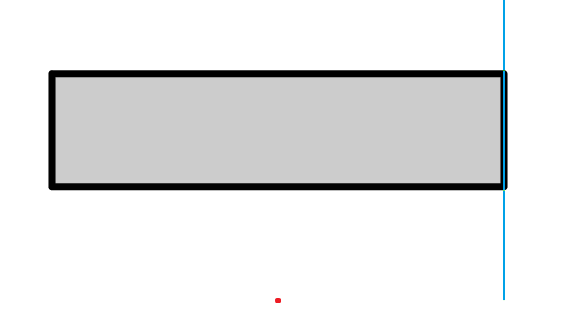
यह कार्य भी एक आसान नहीं है - केवल 23 लोगों ने इसे हल किया, पहला 100: 18 में येगोर कुलिकोव था। यहां यह एपिफ़ानोवा व्लादिस्लाव को ध्यान देने योग्य है, जिन्होंने इस समस्या का समाधान, दौरे के अंत से 2 मिनट पहले किया था। व्लादिस्लाव ने क्वालिफाइंग और क्वालिफाइंग दौर दोनों में पहला स्थान हासिल किया।
5) 2012 फाइनल राउंड, "ई"
शफ़ल डेकपार्स:NRU ITMO के छात्र
सर्गेई मेल्नेकोव डेक को मिलाने के कार्य के बारे में
बात करते हैं।
इस कार्य में, आपको डेक मिक्सिंग मैकेनिज्म के बारे में सोचने की जरूरत है, जो आपको इसे पूरी तरह से मिक्स करने की अनुमति देता है (डेक के मध्य से अंत तक कार्ड ब्लॉक्स की न्यूनतम संख्या के लिए (अर्थात, सुनिश्चित करें कि कोई भी दो समान कार्ड एक के बाद एक नहीं चलते हैं, या रिपोर्ट करते हैं कि डेक को पूरी तरह से मिक्स करना असंभव है) । प्रारंभ में, डेक गैर-घटती गरिमा द्वारा सॉर्ट किया जाता है। कार्ड के विभिन्न लाभों की संख्या को देखते हुए, डेक में कार्ड की संख्या, डेक की संख्या।
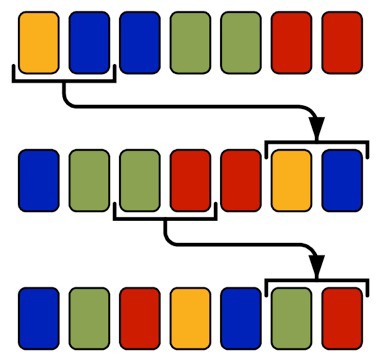 समस्या का विस्तृत विवरण
समस्या का विस्तृत विवरणहम
संघर्ष को एक ऐसी स्थिति कहेंगे जिसमें दो समान कार्ड एक पंक्ति में हैं:
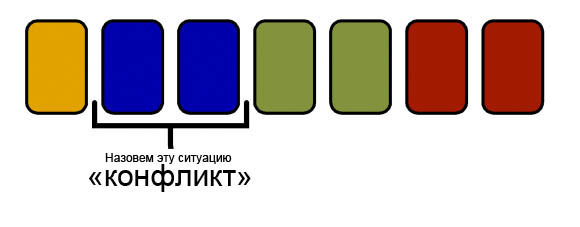
हम
शरीर को कार्ड
के प्रारंभिक अनुक्रम कहते हैं, जिसे हम कार्ड को पूंछ में स्थानांतरित करके धीरे-धीरे कम कर देंगे।
पूंछ बनाई जाएगी ताकि इसमें कार्ड संघर्ष न करें।
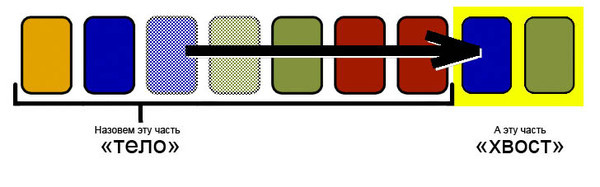
हम मूल अनुक्रम को संघर्षों के अनुक्रम में बदलते हैं और नए अनुक्रम के साथ काम करेंगे। हम संघर्ष के रंग को कार्डों पर लिखी संख्या को कहते हैं जो इसे बनाते हैं। हर बार कार्ड के एक सेगमेंट को डेक के अंत तक स्थानांतरित करते हुए, हम इसके सिरों को संघर्षों के अंदर चुनेंगे।
के। )।
हम एम द्वारा एक रंग की अधिकतम संख्या का विरोध करते हैं और हम इन विरोधों को खुद को "अधिकतम" कहेंगे। हम मामले में समस्या को हल करना सीखते हैं जब एम = / के / 2 problem।
मुझे यह भी याद है कि कार्य की शर्तों के अनुसार, डेक को गैर-घटती गरिमा द्वारा क्रमबद्ध किया जाता है।
उदाहरण के लिए, डेक 1122333344 में, संख्या M 3 (तीन संघर्ष 33) होगी, संघर्षों की कुल संख्या - 6. इस मामले में, M = ⌈K / 2⌉।इस मामले में (उदाहरण नहीं), दो विकल्प हैं:
- K सम है (उदाहरण के रूप में)। हम रंग ए में "अधिकतम" से पहले आने वाले सभी संघर्षों को रंग देते हैं, रंग बी में "अधिकतम" संघर्ष, और बाद के रंग सी। ए | + | बी | + | सी | = | के |, इसलिए | ए | + | सी | = | बी | = एम। उपरोक्त उदाहरण में, 1122333344 के लिए रंग योजना AABBBC होगी। हम जोड़े में संघर्ष को समाप्त करेंगे: पहले जोड़े (बी, सी), फिर, जब ऐसी जोड़ी नहीं बची है, तो जोड़े (ए, बी)। ध्यान दें कि पूंछ में फॉर्म (बी, सी) * (ए, बी) * होगा, जहां * एक या एक से अधिक दोहराव हैं। हमारे उदाहरण में, ये हैं: 1122333344 (AABBC) -> 1122333-4.34 (AAB) -> 1-2333-4.3412 (BB) (हाइफ़न उन स्थानों को इंगित करते हैं जहाँ कार्ड को टेल में स्थानांतरित करने से पहले कार्ड से लिया गया था। डॉट शरीर और पूंछ विभाजक है)। जाहिर है, एक ही रंग के दो संघर्ष एक पंक्ति में नहीं जाते हैं। जब शरीर के साथ जोड़ा जाता है, तो सब कुछ ठीक हो जाएगा: अगर | C | > 0, तब मान C वाला अंतिम कार्ड यथावत रहेगा, और पूंछ B से शुरू होगी। हालाँकि, C | = 0, फिर पूंछ में फॉर्म (ए, बी) * है, जबकि बी के मूल्य वाला अंतिम कार्ड यथावत रहेगा।
- K विषम है। एक समान रंग लागू करें। यदि रंग ए का कम से कम एक कार्ड है, तो हम शुरुआत में आभासी कार्ड और ए-संघर्ष को जोड़कर पिछले मामले में समस्या को कम करते हैं। यदि कोई रंग C कार्ड है, तो अंत में एक नया वर्चुअल कार्ड और C- संघर्ष जोड़ें, फिर से पिछले मामले को कम करें।
इन मामलों के समाधान इष्टतम हैं, क्योंकि संचालन की संख्या की निम्न सीमा ⌉K / 2 these तक पहुंच जाती है। कुल मिलाकर, हम समस्या का समाधान करने में सक्षम हैं जब "अधिकतम" संघर्षों की संख्या सभी संघर्षों का आधा है (राउंड अप के साथ)। हम ऐसे मामले को बुनियादी कहेंगे।
अब हम एक पंक्ति में एक ही मूल्य के अधिकतम कार्डों द्वारा प्रारंभिक स्थितियों को वर्गीकृत करते हैं। हम इन कार्डों को अधिकतम कहेंगे और क्यू के रूप में उनकी संख्या को निरूपित करेंगे
- क्यू = 0. कोई संघर्ष नहीं है, कुछ भी करने की आवश्यकता नहीं है।
- यदि Q> QN / 2⌉ है, तो समस्या का कोई हल नहीं है। इस मामले में, हमारे पास Q - 1 से कम नहीं अधिकतम कार्ड हैं, जो कि अधिकतम मूल्य के अलग कार्ड के लिए पर्याप्त नहीं है।
- क्यू = ⌈N / 2⌉। इस मामले में, अधिकतम कार्ड पर्याप्त नहीं हैं, लेकिन प्रत्येक दूसरा कार्ड अधिकतम होना चाहिए। कार्ड को तीन रंगों में चित्रित करने से हमें मिलता है:
- एक ए कार्ड अधिकतम तक पहुँचने,
- b = Q B- कार्ड जो अधिकतम होते हैं
- c अधिकतम के बाद C- कार्ड।
- इसके अलावा, हम मानते हैं कि सभी A- और C- कार्ड का टकराव होता है। निम्नलिखित मामलों पर विचार करें:
- a = 0. परिणामस्वरूप, c = N - Q = /N / 2 and, और फिर b, c से एक से अधिक नहीं होता है, अर्थात, हमने इसे आधार मामले में घटा दिया है।
- ग = ० । पिछले मामले के समान।
- ए> 0, बी> 0 ए-कार्ड्स में ए - 1 संघर्ष, बी: बी - 1 के बीच, सी: सी - 1. (ए - 1) + (सी - 1) = एन - क्यू - 2, से भिन्न Q − 1 , , .
- M < ⌊ ( N + 1) / 2 ⌋. ( ), , .
, ( ) (C
1 , C
2 ). , , . , .
, . Z, (X, Z) Z , Z, Z (X
1 , Z) (X
2 , Z)…. Z- , (X, Y) , (X
k , Z) (X
k+1 , Y), X
k+1 ≠ Z.
, (X, Z) X, Z (M). M ≠ Z, Z (X, Z) (Z, ...) , Z M, (X, Z) (M, Z).
, , ⌈K / 2⌉ .
, , , . , O(N log N). , - , , , , . , , , : . , O(n), .
« »
6) 2013 , , «E»
:— . α . .
, , P
1 , P
2 , ..., P
n . n(n — 1) , — . (i, j) (j, k) , P
i P
j P
j P
k α. n
3 . , (1, i) (j, 1), α . .
, O(n
3 ), , O(n
3 log(1/ε)) , , ( n
3 ), O(n
3 log(n
3 )).
7) 2013 , , «D»
:. , .
, . , , . , . ? . , (1 + , ). , (1 + ).
, , , . , - , , . , , . ( ), . , , , .
. , . — , , , . , . , . . — min( , + ).
. ( — ). , — , — . ( ; , , , , ).
. , , . . , O(1). — + . , O( ).
?19 .