हर कोई बाइट सरणी को बेस 64 स्ट्रिंग में बदलने के लिए एल्गोरिथ्म जानता है। विभिन्न वर्णमालाओं के साथ, पूंछ के पात्रों के साथ और बिना इस एल्गोरिथ्म की बड़ी संख्या में किस्में हैं। एल्गोरिथ्म के ऐसे संशोधन हैं जिनमें वर्णमाला की लंबाई दो की अन्य शक्तियों के बराबर है, उदाहरण के लिए 32, 16। हालांकि, अधिक दिलचस्प संशोधन हैं जिनमें वर्णमाला की लंबाई दो की शक्ति का एक से अधिक नहीं है, जैसे कि एल्गोरिदम
base85 ,
base91 हैं । हालाँकि, मैं एक एल्गोरिथ्म में नहीं आया था जिसमें वर्णमाला मनमानी हो सकती है, जिसमें 256 से अधिक की लंबाई शामिल है। यह कार्य मुझे दिलचस्प लगा और मैंने इसे लागू करने का निर्णय लिया।
तुरंत
स्रोत पर लिंक पोस्ट करें और
js पर डेमो करें । यद्यपि विकसित एल्गोरिथम का अधिक सैद्धांतिक मूल्य है, मैंने इसके कार्यान्वयन के विवरण का वर्णन करना आवश्यक समझा। व्यवहार में, इसका उपयोग किया जा सकता है, उदाहरण के लिए, उन मामलों के लिए जहां बाइट्स में इसके आकार की तुलना में छोटी स्ट्रिंग लंबाई अधिक प्रासंगिक होती है (उदाहरण के लिए, क्वाइन में)।
कस्टम वर्णमाला
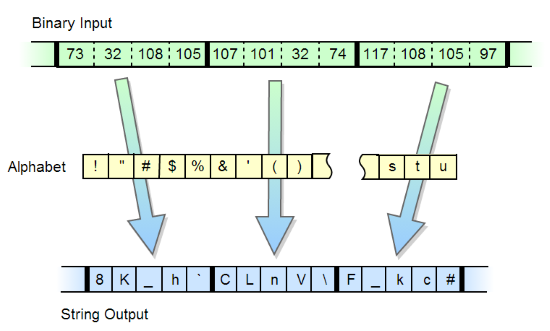
यह समझने के लिए कि इस तरह के एल्गोरिदम को कैसे संश्लेषित किया जा सकता है, मैंने एक विशेष मामले का पता लगाने का फैसला किया, जिसका आधार बेस 85 एल्गोरिदम है। इस एल्गोरिथ्म का विचार निम्नानुसार है: इनपुट डेटा स्ट्रीम को 4 बाइट्स के ब्लॉक में विभाजित किया गया है, फिर उनमें से प्रत्येक को शुरुआत में एक उच्च बाइट के साथ 32-बिट संख्या माना जाता है। 85 द्वारा प्रत्येक ब्लॉक के अनुक्रमिक विभाजन से, 85-दशमलव संख्या प्रणाली के 5 अंक प्राप्त होते हैं। इसके अलावा, प्रत्येक अंक वर्णमाला से मुद्रित प्रतीक, 85 वर्णों के आकार से एन्कोडेड है, और आउटपुट स्ट्रीम में आउटपुट है, ऑर्डर के संरक्षण के साथ, उच्चतम क्रम से निम्नतम तक।
लेकिन 4 बाइट्स का आकार क्यों चुना गया था, अर्थात्। 32 बिट्स? और क्योंकि एक ही समय में इष्टतम संपीड़न हासिल किया जाता है, अर्थात्। बिट्स की न्यूनतम संख्या (2 ^ 32 = 4294967296) अधिकतम वर्णों (85 ^ 5 = 4437053125) के साथ प्रयोग की जाती है। हालाँकि, इस तकनीक को किसी अन्य वर्णमाला तक बढ़ाया जा सकता है। इस प्रकार, एक गणितीय प्रणाली को बिट्स की संख्या की खोज करने के लिए संकलित किया गया था जिस पर संपीड़न अधिकतम होगा:
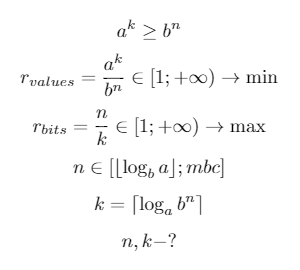 a
a वर्णमाला
A का आकार है
।k एन्कोडेड वर्णों की संख्या है।
b - संख्या प्रणाली का आधार।
n वर्णमाला
A के k वर्णों को दर्शाने के लिए संख्या प्रणाली
b में बिट्स की संख्या है
।आर संपीड़न अनुपात (अधिक बेहतर) है।
mbc बिट्स में अधिकतम ब्लॉक आकार है।
⌊X (x (तल) से कम का सबसे बड़ा पूर्णांक है।
⌈X x x (छत) से बड़ा सबसे छोटा पूर्णांक है।
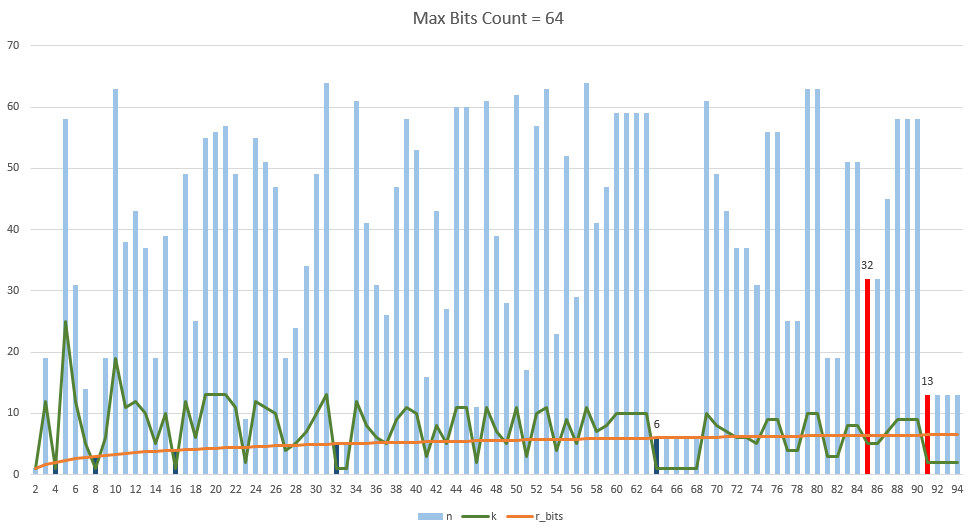
आगे, इस तकनीक का उपयोग करते हुए, बिट्स और वर्णों के इष्टतम संयोजन पाए गए, जो नीचे दिए गए चित्र में दर्शाए गए थे। अधिकतम ब्लॉक आकार 64 बिट्स है (इस संख्या को इस तथ्य के कारण चुना गया था कि बड़ी संख्या के साथ बड़ी संख्या का उपयोग करना आवश्यक है)। जैसा कि आप देख सकते हैं, संपीड़न अनुपात हमेशा वर्णों की संख्या में वृद्धि के साथ नहीं बढ़ता है (यह 60 और 91 के क्षेत्र में देखा जा सकता है)। लाल पट्टियाँ अच्छी तरह से ज्ञात एन्कोडिंग (85 और 91) को दर्शाती हैं। दरअसल, आरेख से यह निष्कर्ष निकाला जा सकता है कि इन एन्कोडिंग के लिए इस तरह के कई पात्रों को व्यर्थ नहीं चुना गया था, क्योंकि यह न्यूनतम संपीड़न अनुपात के साथ न्यूनतम संख्या में बिट्स का उपयोग करता है। यह ध्यान देने योग्य है कि अधिकतम ब्लॉक आकार में वृद्धि के साथ, आरेख बदल सकता है (उदाहरण के लिए, 64 बिट्स के साथ base85 एन्कोडिंग के लिए, ब्लॉक आकार 32 बिट्स होगा, और वर्णों की संख्या 1.25 के अतिरेक के साथ 5 होगी। अधिकतम ब्लॉक आकार 256 बिट्स तक बढ़ जाता है, तो ब्लॉक का आकार 22 अक्षरों के साथ 141 बिट और 1.2482 का अतिरेक) होगा।
कोडिंग कदम
तो, चरणों में, एन्कोडिंग प्रक्रिया इस प्रकार है:
- इष्टतम ब्लॉक आकार (बिट्स एन की संख्या) की गणना और इसके अनुरूप वर्णों की संख्या ( के )।
- स्रोत स्ट्रिंग का प्रतिनिधित्व बाइट्स के एक क्रम के रूप में (UTF8 का उपयोग करके)।
- N बिट्स के समूहों में बाइट्स के मूल अनुक्रम को विभाजित करना।
- आधार के साथ संख्या प्रणाली के साथ बिट्स के प्रत्येक समूह को एक संख्या में बदलें।
- पूंछ बिट्स की मिसअलाउंसिंग।
पहले चरण के कार्यान्वयन के ऊपर चर्चा की गई थी। दूसरे चरण के लिए, विधि को बाइट्स के एक सरणी के रूप में स्ट्रिंग का प्रतिनिधित्व करने के लिए इस्तेमाल किया गया था (सी # में यह अंतर्निहित
Encoding.UTF8.GetBytes () में है , और जेएस के लिए इसे
strToUt8Bytes और
bytesToUtf8Str द्वारा मैन्युअल रूप से लिखा गया था)। अगला, अगले तीन चरणों को और अधिक विस्तार से माना जाएगा। वर्णों के एक क्रम को बाइट्स के एक सरणी में उलटा रूपांतरण समान दिखता है।
बिट ब्लॉक एनकोडिंग
private void EncodeBlock(byte[] src, char[] dst, int ind) { int charInd = ind * BlockCharsCount; int bitInd = ind * BlockBitsCount; BigInteger bits = GetBitsN(src, bitInd, BlockBitsCount); BitsToChars(dst, charInd, (int)BlockCharsCount, bits); } private void DecodeBlock(string src, byte[] dst, int ind) { int charInd = ind * BlockCharsCount; int bitInd = ind * BlockBitsCount; BigInteger bits = CharsToBits(src, charInd, (int)BlockCharsCount); AddBitsN(dst, bits, bitInd, BlockBitsCount); }
GetBitsN ब्लॉकबिट्स बिट की एक लंबी संख्या देता है और बिट बिट के साथ शुरू होता है।
AddBitsN स्थिति बिट में
dst बाइट
सरणी के लिए
ब्लॉक बिट्स बिट की लंबाई के
बिट्स की संख्या को
जोड़ता है ।
मनमाने आधार और इसके विपरीत संख्या प्रणाली में बिट्स के ब्लॉक को परिवर्तित करना
वर्णमाला एक मनमाना वर्णमाला है। उलटा परिवर्तन के लिए, पहले से गणना की गई व्युत्क्रम वर्णमाला
InvAlphabet का उपयोग किया जाता है । यह ध्यान देने योग्य है कि, उदाहरण के लिए, बेस 64 के लिए, बिट्स के प्रत्यक्ष क्रम का उपयोग किया जाता है, और बेस 85 के लिए, रिवर्स ऑर्डर का उपयोग किया जाता है (
ReverseOrder ),
_powN वर्णमाला की लंबाई है।
private void BitsToChars(char[] chars, int ind, int count, BigInteger block) { for (int i = 0; i < count; i++) { chars[ind + (!ReverseOrder ? i : count - 1 - i)] = Alphabet[(int)(block % CharsCount)]; block /= CharsCount; } } private BigInteger CharsToBits(string data, int ind, int count) { BigInteger result = 0; for (int i = 0; i < count; i++) result += InvAlphabet[data[ind + (!ReverseOrder ? i : count - 1 - i)]] * _powN[BlockCharsCount - 1 - i]; return result; }
टेल बिट प्रसंस्करण
इस समस्या को हल करने के लिए ज्यादातर समय बिताया गया था। हालांकि, अंत में, वास्तविक संख्याओं का उपयोग किए बिना मुख्य और पूंछ के बिट्स और पात्रों की गणना के लिए कोड बनाने के लिए निकला, जिससे एल्गोरिदम को समानांतर करना आसान हो गया।
- mainBitsLength - बिट्स की मुख्य संख्या।
- tailBitsLength - बिट्स की पूंछ संख्या।
- mainCharsCount - पात्रों की मुख्य संख्या।
- tailCharsCount - पात्रों की पूंछ संख्या।
- GlobalBitsLength - बिट्स की कुल संख्या (mainBitsLength + tailBitsLength)।
- GlobalCharsCount - वर्णों की कुल संख्या (mainCharsCount + tailCharsCount)।
एन्कोडिंग के दौरान बिट्स और प्रतीकों की मुख्य और पूंछ संख्या की गणना।
int mainBitsLength = (data.Length * 8 / BlockBitsCount) * BlockBitsCount; int tailBitsLength = data.Length * 8 - mainBitsLength; int globalBitsLength = mainBitsLength + tailBitsLength; int mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; int tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; int globalCharsCount = mainCharsCount + tailCharsCount; int iterationCount = mainCharsCount / BlockCharsCount;
डिकोडिंग के दौरान बिट्स और प्रतीकों की मुख्य और पूंछ संख्या की गणना।
int globalBitsLength = ((data.Length - 1) * BlockBitsCount / BlockCharsCount + 8) / 8 * 8; int mainBitsLength = globalBitsLength / BlockBitsCount * BlockBitsCount; int tailBitsLength = globalBitsLength - mainBitsLength; int mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; int tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; BigInteger tailBits = CharsToBits(data, mainCharsCount, tailCharsCount); if (tailBits >> tailBitsLength != 0) { globalBitsLength += 8; mainBitsLength = globalBitsLength / BlockBitsCount * BlockBitsCount; tailBitsLength = globalBitsLength - mainBitsLength; mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; } int iterationCount = mainCharsCount / BlockCharsCount;
जावास्क्रिप्ट कार्यान्वयन
मैंने इस कलन विधि को जावास्क्रिप्ट में बनाने का निर्णय लिया। बड़ी संख्या में काम करने के लिए,
jsbn लाइब्रेरी का
उपयोग किया गया था। इंटरफ़ेस बूटस्ट्रैप का उपयोग करता है। परिणाम यहाँ देखा जा सकता है:
kvanttt.imtqy.com/BaseNcodingनिष्कर्ष
यह एल्गोरिथ्म इसलिए लिखा गया है ताकि अन्य भाषाओं में पोर्ट करना आसान हो जाए और इसे (C # संस्करण में) GPU सहित समांतर कर दिया जाए। वैसे, C # का उपयोग करके GPU के लिए बेस 64 एल्गोरिदम को संशोधित करने के बारे में यह यहाँ अच्छी तरह से लिखा गया है:
बेस 64 एनकोडिंग एक जीपीयू पर ।
विकसित एल्गोरिथ्म की शुद्धता का परीक्षण बेस 32, बेस 64, बेस 85 एल्गोरिदम पर किया गया था (परिणामस्वरूप वर्णों के अनुक्रम पूंछ के अलावा समान थे)।