
प्रोग्रामरों के लिए सबसे बड़ा रूसी ओलंपियाड का अगला सीज़न, रूसी कोड कप शनिवार, 19 अप्रैल 2014 को शुरू हुआ। नए दिलचस्प और गैर-तुच्छ कार्यों, असम्बद्ध संघर्ष और महान पुरस्कारों से आगे।
रूसी कोड कप के जूरी ने सभी प्रतिभागियों के लिए एक आश्चर्य तैयार किया: 17 अप्रैल को, उनमें से प्रत्येक को अपनी ताकत का मूल्यांकन करने का अवसर मिला। 19:30 मास्को समय में, ओलंपियाड का एक प्रशिक्षण दौर
http://codeforces.ru पर आरसीसी के रचनाकारों के कार्यों के एक नए हिस्से के साथ हुआ।
आरसीसी 2014 वार्मअप एक ऐसा परीक्षण है जिसने आपके हाथ की कोशिश करना और यह समझना संभव बना दिया है कि चैंपियनशिप के दौर में क्या तैयार किया जाए। और "अनुभवी" प्रतिभागियों के लिए, वह आरसीसी 2014 की पहली लड़ाई से पहले प्रशिक्षित और गर्म करने का एक आदर्श अवसर था।
इसके अलावा, अगर प्रतिभागियों के लिए रूसी कोड कप कार्यों को केवल रूसी में पेश किया जाता है, तो वार्मअप राउंड कार्यों में रूसी और अंग्रेजी दोनों में थे, जो स्थल के भूगोल का काफी विस्तार करते थे। राउंड के लिए कुल 3265 प्रतिभागियों ने पंजीकरण कराया।
कार्यों की स्थितियां बहुत भिन्न थीं: 2214 के रूसी कोड कप फाइनल के लिए प्रतिभागियों के चयन में मदद करना आवश्यक था, गिरने के बाद परीक्षण प्रणाली के आंकड़ों को बहाल करने के लिए, रूसी कोड कप के प्रतिभागियों के बीच एक फुटबॉल टूर्नामेंट आयोजित करने के लिए, चालाक लड़के जीन को टी-शर्ट प्राप्त करने में मदद करने के लिए, लड़के मिशा के दिलचस्प कार्य को हल करने के लिए। रूसी कोड कप के फाइनल के बाद नाव से यात्रा करें, बड़ी संख्या में होटल में रूसी कोड कप 2214 के फाइनल का आयोजन करें और अपने विकास के दौरान कार्यों तक पहुंचने के लिए पासवर्ड प्राप्त करें (बाद वाला सफल नहीं हुआ)।
तो, आइए देखें कि चैंपियनशिप में भाग लेने के लिए तैयारी करना सबसे अच्छा कैसे था।
कार्य 1.
चयनविश्लेषण: सबसे पहले, यह ध्यान दिया जाना चाहिए कि यदि k n / m से अधिक या बराबर है, तो इसका उत्तर है 0. हमें केवल n • m - k लोगों को डायल करने की आवश्यकता है। उन्हें डायल करने के तीन तरीके हैं:
• केवल पहले प्रकार के गोल लें:
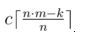
• n द्वारा विभाज्य संख्या के लिए दूसरे प्रकार का थोड़ा चक्कर लें:
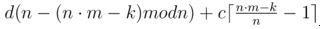
• दूसरे प्रकार के केवल राउंड लें: d (n • m - k)।
इस समस्या में भी एक संपूर्ण समाधान लिखना संभव था - हम पहले प्रकार के कितने राउंड लेते हैं, और दूसरे के कितने राउंड।
कार्य 2.
असफलताविश्लेषण: हम 105 तत्वों की एक सरणी शुरू करते हैं, शुरू में -1 से भरा होता है, और नंबर k के साथ सेल में हम के-वें प्रतिभागी के भेजने की अधिकतम संख्या को संग्रहीत करेंगे, जो अब है। हम पार्सल को क्रमिक रूप से संसाधित करेंगे। पार्सल xk को संसाधित होने दें। यदि [k] <x - 1 है, तो यह स्पष्ट है कि उत्तर नहीं है, अन्यथा हम सरणी को अपडेट करते हैं - एक [k] = अधिकतम ([k], x)।
टास्क 3.
फुटबॉलविश्लेषण: एक टूर्नामेंट की कल्पना एक ग्राफ के रूप में करें। प्रत्येक शीर्ष से बिल्कुल के आउटगोइंग किनारे हैं। फिर सभी एनके किनारों। पूर्ण स्तंभ अधिकतम में
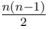
किनारों, इसलिए यदि n <2k + 1, तो उत्तर -1 है। अन्यथा, यदि आवश्यक हो तो i-वें शीर्ष को i + 1, ..., i + k, और लूप से कनेक्ट करें।
टास्क 4.
मुश्किल जीनपार्सिंग: आइए दोस्तों को आवश्यक संख्याओं पर नज़र रखते हुए क्रमबद्ध करें। हम मुखौटे पर गतिशीलता पर विचार करेंगे - ऐसी और ऐसी समस्याओं को हल करने के लिए आपको कितनी न्यूनतम राशि का भुगतान करना होगा, अगर हमने पहले i दोस्तों को लिया। तब उत्तर की तुलना पहले i दोस्तों के लिए जवाब के साथ की जानी चाहिए और साथ ही मॉनिटर की संख्या जो आई-वें दोस्त की आवश्यकता होती है। यह ध्यान रखना मुश्किल नहीं है कि यदि आप दोस्तों को अनुक्रम में लेते हैं, तो आप बैकपैक के रूप में गतिशीलता को पुनर्गणना कर सकते हैं। इस एल्गोरिथ्म का रनिंग टाइम O (nlog (n) + n2m) है।
टास्क 5.
स्क्वायर टेबलविश्लेषण: चलो किसी भी n के लिए लंबाई n की एक सरणी बनाते हैं जैसे कि उस पर संख्याओं के वर्गों का योग एक वर्ग है:
• यदि n = 1 है, तो हम [1] लेते हैं।
• यदि n = 2 है, तो हम [3, 4] लेते हैं।
• यदि n सम है, तो हम लेते हैं
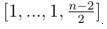
।
• यदि n विषम है, तो लें
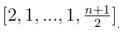
।
हमें 2 नंबर n और m दिए गए हैं। संख्या n के अनुरूप एक सरणी दें, और संख्या m के अनुरूप करें।
फिर हम अंतिम सरणी c का निर्माण निम्न तरीके से करते हैं - cij = ai • bj।
कार्य: 6.
आयोजकों की बड़ी समस्याएंविश्लेषण: इस समस्या के दो समाधान हैं।
पहला वाला। कुछ शीर्ष के लिए निलंबित करें। आइए हम प्रत्येक 3 के लिए इसकी उप-सीमा में सबसे दूर लंबवत गणना करें, साथ ही प्रत्येक शीर्ष के लिए गहराई। हम बाइनरी अपसर्ज के लिए सरणियों की गणना भी करते हैं। प्रत्येक शीर्ष I और 2 2j की डिग्री के लिए, हम निम्नलिखित सरणियों की गणना करते हैं - p [i] [j], up [i] [j] और down [i] [j]। p [i] [j] २j की दूरी पर शीर्ष i का पूर्वज है। ऊपर [i] [j], i से सबसे लंबा पथ उन वर्तनियों को संग्रहीत किया जाएगा, जो कि i और p [i] [j] के बीच के मार्ग पर हैं। नीचे [i] [j] ऊपर से अलग है [i] [j], जो शीर्ष p [i] [j] से पथ को संग्रहीत करता है।
अब यह छोटे पर निर्भर है हम एक यूवी अनुरोध प्राप्त करते हैं, हम इसके सबसे छोटे सामान्य पूर्वज - डब्ल्यू की तलाश कर रहे हैं। यह चोटी हू को खोजने के लिए बनी हुई है, जो इस रास्ते के बीच में होगी। इस शीर्ष पर पेड़ को ट्रिम करें, और अपने पेड़ में वर्टेक्स यू से सबसे लंबी दूरी और उसके पेड़ में वर्टेक्स वी से सबसे लंबी दूरी की गणना करें। इसे पेड़ पर प्रस्तुत करते हुए, यदि हम नहीं हटाते हैं, तो हम अपने पूर्व-परिकलित सरणियों का उपयोग करके, सबसे लंबे पथ के मूल्य को सही ढंग से पुनर्गणना कर सकते हैं।
समाधान O (nlog (n)) है।
दूसरा वाला। संक्षेप में। इस वृक्ष का व्यास ज्ञात कीजिए। हम प्रत्येक शीर्ष के लिए उपसर्ग पर वहां उत्तर की गणना करते हैं। फिर, अनुरोध का उत्तर देते समय, हम पाते हैं कि पथ का व्यास क्या है। इस खंड पर हम मध्य शिखर पाते हैं, और फिर उपसर्ग या प्रत्यय के साथ अनुरोध का जवाब देते हैं।
टास्क: 7.
मुश्किल पासवर्डविश्लेषण: इस समस्या का प्रमुख सैद्धांतिक विचार यह है कि दूसरी पंक्ति 4, 3 के साथ 5, आदि के साथ मेल खाती है, इसलिए, हमें केवल पहली तीन पंक्तियों में कुछ बदलने में सक्षम होने की आवश्यकता है।
अब मामला व्यावहारिक हिस्सा बना हुआ है। सबसे पहले, हम सभी मूल्यों को संपीड़ित करेंगे ताकि वे 105 से अधिक न हों। हम सरणी को लंबाई के खंडों में विभाजित करते हैं। प्रत्येक खंड पर, हम निम्नलिखित पर विचार करेंगे - प्रत्येक मान के लिए हम कितने बार इसे cnt उपसर्ग पर, साथ ही साथ Fenwick पेड़ में संग्रहीत करेंगे, जिसमें इस उपसर्ग पर संख्याओं की संख्या जो ठीक के समय k होती है, को सेल f [k] में संग्रहीत किया जाएगा। यह नोटिस करना आसान है कि दूसरी पंक्ति में प्रश्नों का उत्तर पहली सरणी में संग्रहीत है, और तीसरी पंक्ति के लिए उत्तर प्राप्त करने के लिए, आपको f [cnt [k] ... 105] की गणना करने की आवश्यकता है। यह भी स्पष्ट है कि इस गतिशीलता को कैसे पुनर्गठित किया जाए।
कुल, हमें एक अनुरोध के लिए समय मिलता है
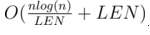
। अगर हम लेते हैं
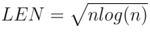
, तो अनुरोध करने के लिए प्रतिक्रिया समय होगा
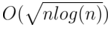
।