ご挨拶!
私の論文では、データクラスタリングアルゴリズムのレビューと比較分析を実施しました。 すでに資料を収集して作成したことが、誰かにとって興味深く有用なものになると思いました。
クラスタリングとは、
sashaeveが記事
「クラスタリング:k-meansとc-means」で述べています。 アレキサンダーの言葉を部分的に繰り返し、部分的に補足します。 また、この記事の最後で、関心のある人は、参照リストのリンクから資料を読むことができます。
また、ドライな「卒業証書」スタイルのプレゼンテーションを、よりジャーナリスティックなものにすることを試みました。
クラスタリングの概念
クラスタリング(またはクラスター分析)は、複数のオブジェクトをクラスターと呼ばれるグループに分解するタスクです。 各グループ内には「類似の」オブジェクトがあり、異なるグループのオブジェクトは可能な限り異なる必要があります。 クラスタリングと分類の主な違いは、グループのリストが明確に定義されておらず、アルゴリズムの動作中に決定されることです。
一般的なクラスター分析の適用は、次の手順に限定されます。
- クラスタリング用のオブジェクトの選択を選択します。
- サンプル内のオブジェクトが評価される変数のセットの定義。 必要に応じて、変数の値を正規化します。
- オブジェクト間の類似性の尺度の値の計算。
- 同様のオブジェクト(クラスター)のグループを作成するためのクラスター分析方法の適用。
- 分析結果のプレゼンテーション。
結果を受け取って分析した後、選択したメトリックとクラスタリング方法を調整して、最適な結果を得ることができます。
距離測定
それでは、オブジェクトの「類似性」をどのように判断するのでしょうか? まず、各オブジェクトの特性のベクトルを作成する必要があります-原則として、これは数値のセット、たとえば、人の身長と体重です。 ただし、定性的(いわゆるカテゴリー)特性で機能するアルゴリズムもあります。
特性のベクトルを決定したら、すべてのコンポーネントが「距離」の計算に同じ貢献をするように正規化できます。 正規化プロセスでは、すべての値が特定の範囲、たとえば[-1、-1]または[0、1]に縮小されます。
最後に、オブジェクトの各ペアについて、それらの間の「距離」が測定されます-類似度。 多くのメトリックがありますが、ここに主要なメトリックのみを示します。
- ユークリッド距離
最も一般的な距離関数。 多次元空間の幾何学的距離を表します:
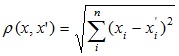
- ユークリッド距離の二乗
互いに離れているオブジェクトにより大きな重みを与えるために使用されます。 この距離は次のように計算されます。

- 都市ブロック距離(マンハッタン距離)
この距離は、座標の差の平均です。 ほとんどの場合、この距離の測定により、通常のユークリッド距離と同じ結果が得られます。 ただし、この測定では、個々の大きな差(放射)の影響は低減されます(二乗されていないため)。 マンハッタン距離の計算式:

- チェビシェフ距離
この距離は、1つの座標が異なる2つのオブジェクトを「異なる」ものとして定義する必要がある場合に役立ちます。 チェビシェフ距離は次の式で計算されます。

- パワー距離
対応するオブジェクトが非常に異なる次元に関連する重みを増減する必要がある場合に使用されます。 パワー距離は、次の式で計算されます。
 、
、
ここで、rとpはユーザー定義のパラメーターです。 パラメーターpは、個々の座標による差異の段階的な重み付けを担当し、パラメーターrは、オブジェクト間の大きな距離の累進的な重み付けを担当します。 両方のパラメーター-rとp-が2に等しい場合、この距離はユークリッド距離と一致します。
メトリックの選択は完全に研究者次第です。異なるメジャーを使用すると、クラスタリングの結果が大幅に異なる可能性があるためです。
アルゴリズム分類
私自身は、クラスタリングアルゴリズムの2つの主要な分類を特定しました。
- 階層的でフラット。
階層アルゴリズム(分類アルゴリズムとも呼ばれます)は、サンプルの1つのパーティションだけをばらばらのクラスターに構築するのではなく、ネストされたパーティションのシステムを構築します。 T.O. 出力では、クラスターのツリーを取得します。クラスターのルートはサンプル全体で、葉は最小のクラスターです。
フラットアルゴリズムは、オブジェクトの1つのパーティションをクラスターに構築します。 - 明確であいまいです。
明確な(またはばらばらの)アルゴリズムは、クラスター番号を各サンプルオブジェクトに関連付けます。 各オブジェクトは1つのクラスターのみに属します。 ファジー(または交差)アルゴリズムは、各オブジェクトに、オブジェクトとクラスターの関係の度合いを示す実際の値のセットを関連付けます。 つまり 各オブジェクトは、何らかの確率で各クラスターに属します。
クラスタリング
階層型アルゴリズムの場合、クラスターの結合方法、クラスター間の「距離」の計算方法に関する問題が発生します。 いくつかのメトリックがあります。
- 単一の通信(最近傍距離)
この方法では、2つのクラスター間の距離は、異なるクラスター内の2つの最も近いオブジェクト(最近傍)間の距離によって決まります。 結果のクラスターは連鎖する傾向があります。
- 完全なコミュニケーション(最も遠い隣人の距離)
この方法では、クラスター間の距離は、異なるクラスター内の2つのオブジェクト間の最大距離(つまり、最も遠い隣人)によって決定されます。 通常、この方法は、オブジェクトが別々のグループに属する場合に非常に効果的です。 クラスターが細長い場合、またはその自然なタイプが「チェーン」の場合、この方法は不適切です。
- 非加重ペアワイズ平均
この方法では、2つの異なるクラスター間の距離は、クラスター内のオブジェクトのすべてのペア間の平均距離として計算されます。 この方法は、オブジェクトが異なるグループを形成する場合に効果的ですが、拡張(「チェーン」タイプ)クラスターの場合にも同様に機能します。
- 加重ペアワイズ平均
この方法は、計算で対応するクラスターのサイズ(つまり、クラスターに含まれるオブジェクトの数)が重み係数として使用されることを除いて、重みなしのペア平均法と同じです。 したがって、不均等なクラスターサイズが想定される場合、この方法を使用する必要があります。
- 重みなし重心法
この方法では、2つのクラスター間の距離は、重心間の距離として定義されます。
- 加重重心法(中央値)
この方法は、クラスターサイズ間の違いを計算するために計算を使用することを除いて、前の方法と同じです。 したがって、クラスタサイズに大きな違いがあるか、または疑われる場合、この方法は前の方法よりも望ましい方法です。
アルゴリズムの概要
階層的クラスタリングアルゴリズム
階層的クラスタリングアルゴリズムの中で、2つの主要なタイプが区別されます:アップストリームアルゴリズムとダウンストリームアルゴリズム。 トップダウンアルゴリズムは、「トップダウン」の原則に従って動作します。最初は、すべてのオブジェクトが1つのクラスターに配置され、その後、クラスターはより小さなクラスターに分割されます。 アップストリームアルゴリズムはより一般的で、作業の開始時に各オブジェクトを個別のクラスターに配置し、選択内のすべてのオブジェクトが1つのクラスターに含まれるまでクラスターを大きなクラスターに結合します。 したがって、ネストされたパーティションのシステムが構築されます。 このようなアルゴリズムの結果は通常、樹形図の形で表示されます。 このようなツリーの典型的な例は、動植物の分類です。
多くの場合、クラスター間の距離を計算するために、単一リンクまたは完全リンクの2つの距離を使用します(クラスター間の距離の測定の概要を参照)。
階層アルゴリズムの欠点は、完全なパーティションのシステムであり、解決される問題のコンテキストでは冗長になる場合があります。
二次誤差アルゴリズム
クラスタリングタスクは、オブジェクトの最適なパーティションをグループに構築することと考えることができます。 さらに、最適性は、パーティションの平均二乗誤差を最小化するための要件として定義できます。
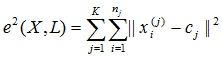
ここで、
c jはクラスター
j (特定のクラスターの特性の平均値を持つポイント)の「重心」です。
二次誤差アルゴリズムは、フラットアルゴリズムの一種です。 このカテゴリで最も一般的なアルゴリズムはk-means法です。 このアルゴリズムは、相互に可能な限り離れた場所に特定の数のクラスターを構築します。 アルゴリズムはいくつかの段階に分かれています。
- クラスタの最初の「重心」であるk個の点をランダムに選択します。
- 最も近い「重心」を持つクラスターに各オブジェクトを割り当てます。
- 現在の構成に従ってクラスターの「重心」を再計算します。
- アルゴリズムを停止するための基準が満たされていない場合は、手順2に戻ります。
アルゴリズムの動作を停止する基準として、通常、標準誤差の最小変化が選択されます。 手順2でクラスターからクラスターに移動するオブジェクトがなかった場合、アルゴリズムの動作を停止することもできます。
このアルゴリズムの欠点には、パーティションのクラスター数を指定する必要があることが含まれます。
ファジーアルゴリズム
最も一般的なファジークラスタリングアルゴリズムは、c-meansアルゴリズムです。 これはk-means法の修正です。 アルゴリズムの手順:
- サイズnxkのメンバーシップ行列Uを選択して、 n個のオブジェクトからk個のクラスターへの初期ファジーパーティションを選択します。
- 行列Uを使用して、ファジー誤差基準の値を見つけます。
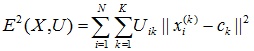 、
、
ここで、 c kはファジークラスターkの 「重心」です。
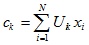 。
。 - ファジーエラー基準のこの値を減らすために、オブジェクトを再グループ化します。
- 行列Uの変更が重要でなくなるまで、手順2に戻ります。
クラスタの数が事前にわからない場合、または各オブジェクトを1つのクラスタに明確に割り当てる必要がある場合、このアルゴリズムは適切ではない可能性があります。
グラフベースのアルゴリズム
このようなアルゴリズムの本質は、オブジェクトのサンプルがグラフ
G =(V、E)の形で表され、その頂点がオブジェクトに対応し、エッジの重みがオブジェクト間の「距離」に等しいことです。 グラフクラスタリングアルゴリズムの利点は、可視性、実装の相対的な容易さ、および幾何学的な考慮事項に基づいてさまざまな改善を行うことができることです。 主なアルゴリズムは、接続されたコンポーネントを選択するためのアルゴリズム、最小スパニングツリーを構築するためのアルゴリズム、およびレイヤーごとのクラスタリングアルゴリズムです。
接続コンポーネントアルゴリズム
接続コンポーネントを選択するアルゴリズムでは、入力パラメーター
Rが設定され、グラフでは、「距離」が
Rよりも大きいすべてのエッジが削除されます。 オブジェクトの最も近いペアのみが接続されたままです。 アルゴリズムの意味は、グラフがいくつかの接続されたコンポーネントに「バラバラになる」すべての「距離」の範囲にある
Rの値を選択することです。 結果のコンポーネントはクラスターです。
パラメーター
Rを選択するには、通常、ペアワイズ距離の分布のヒストグラムを作成します。 明確に定義されたクラスターデータ構造の問題では、ヒストグラムには2つのピークがあります。1つはクラスター内距離に対応し、2つ目はクラスター間距離に対応します。 パラメータ
Rは 、これらのピーク間の最小ゾーンから選択されます。 同時に、距離のしきい値を使用してクラスターの数を制御することはかなり困難です。
最小スパニングツリーアルゴリズム
最小スパニングツリーアルゴリズムは、最初にグラフ上に最小スパニングツリーを構築し、次に最大の重みを持つエッジを順次削除します。 この図は、9つのオブジェクトについて取得された最小スパニングツリーを示しています。
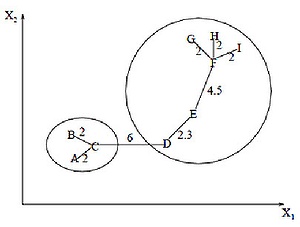
6単位の長さ(最大距離のエッジ)のラベルが付けられた結合を削除することにより、{A、B、C}と{D、E、F、G、H、I}の2つのクラスターを取得します。 2番目のクラスターは、4.5単位に等しい長さのエッジEFを削除することにより、さらに2つのクラスターに分割できます。
レイヤーごとのクラスタリング
レイヤーごとのクラスタリングアルゴリズムは、オブジェクト(頂点)間の一定レベルの距離でのグラフの接続されたコンポーネントの割り当てに基づいています。 距離レベルは、距離のしきい値
cによって設定され
ます 。 たとえば、オブジェクト間の距離
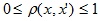
それから
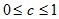
。
レイヤーごとのクラスタリングアルゴリズムは、クラスター間の階層関係を反映する列
Gのサブグラフのシーケンスを形成します。

、
ここで、
G t =(V、E t )は
tのレベルのグラフです。

、
t -t番目の距離しきい値
mは階層レベルの数、
G 0 =(V、o) 、oは
t 0 = 1で得られたグラフの空のエッジセットです。
G m = G。つまり、
t m = 1であるため、距離(グラフのエッジの長さ)に制限のないオブジェクトのグラフ。
距離のしきい値{
s 0 、...、s m }(0 =
s 0 <
s 1 <... <
s m = 1)を変更することにより、結果のクラスターの階層の深さを制御できます。 したがって、レイヤーごとのクラスタリングアルゴリズムは、フラットデータパーティションと階層データパーティションの両方を作成できます。
アルゴリズム比較
アルゴリズムの計算の複雑さ
| クラスタリングアルゴリズム | 計算の複雑さ |
| 階層的 | O(n 2 ) |
| k-means | O(nkl)、kはクラスターの数、lは反復の数 |
|---|
| c-means |
| 接続されたコンポーネントの選択 | アルゴリズムに依存 |
| 最小スパニングツリー | O(n 2 log n) |
| レイヤーごとのクラスタリング | O(最大(n、m))、ここでm <n(n-1)/ 2 |
アルゴリズム比較表
| クラスタリングアルゴリズム | クラスター形状 | 入力データ | 結果 |
| 階層的 | 任意 | クラスターの数または階層を切り捨てるための距離のしきい値 | バイナリクラスターツリー |
| k-means | ハイパースフィア | クラスターの数 | クラスターセンター |
| c-means | ハイパースフィア | クラスターの数、あいまいさの程度 | クラスターセンター、メンバーシップマトリックス |
| 接続されたコンポーネントの選択 | 任意 | 距離のしきい値R | クラスターのツリー構造 |
| 最小スパニングツリー | 任意 | クラスターの数またはエッジ除去の距離のしきい値 | クラスターのツリー構造 |
| レイヤーごとのクラスタリング | 任意 | 距離しきい値シーケンス | 異なるレベルの階層を持つクラスターのツリー構造 |
アプリケーションについて少し
私の仕事では、階層構造(ツリー)から個別の領域を選択する必要がありました。 つまり 基本的に、元のツリーをいくつかの小さなツリーに分割する必要がありました。 指向ツリーはグラフの特殊なケースであるため、グラフ理論に基づいたアルゴリズムが当然適しています。
完全に接続されたグラフとは異なり、すべての頂点が方向付けられたツリーのエッジで接続されているわけではなく、エッジの総数はn – 1です(nは頂点の数です)。 つまり ツリーノードに適用されると、任意の数のエッジを削除するとツリーが接続されたコンポーネント(別のツリー)に「分割」されるため、接続されたコンポーネントを選択するアルゴリズムの操作が簡略化されます。 この場合の最小スパニングツリーアルゴリズムは、接続されたコンポーネントを選択するアルゴリズムと一致します。最も長いエッジを削除することにより、元のツリーはいくつかのツリーに分割されます。 最小のスパニングツリーの構築フェーズがスキップされることは明らかです。
他のアルゴリズムを使用する場合、オブジェクト間の関係の存在を個別に考慮する必要があり、アルゴリズムが複雑になります。
それとは別に、最高の結果を達成するためには、距離測定の選択を試す必要があり、時にはアルゴリズムを変更する必要さえあると言いたいです。 単一のソリューションはありません。
参照資料
1.ボロンツォフK.V.
クラスタリングおよび多次元スケーリングアルゴリズム 。 講義のコース。 モスクワ州立大学、2007年。
2. Jain A.、Murty M.、Flynn P.
データクラスタリング:レビュー 。 // ACM Computing Surveys。 1999. Vol。 31、いいえ。 3。
3. Kotov A.、Krasilnikov N.
データクラスタリング 。 2006年。
3.マンデルI. D.クラスター分析。 -M .:ファイナンスと統計、1988年。
4.応用統計:分類と次元の縮小。 / S.A. Ayvazyan、V.M。 ブフスターバー、I.S。 エンユコフ、L.D。 Meshalkin-M .:金融と統計、1989年。
5.機械学習、パターン認識、データマイニング専用の情報と分析リソース
-www.machinelearning.ru6.中部コバI.A. 情報技術大学の講義コース「データマイニング」
-www.intuit.ru/department/database/datamining