はじめに
このトピックでは、私が参加できて幸運だった、異常なニューラルネットワークのモデルについてお話したいと思います。 このモデルは約1年前に開発されました（原作者は最後のセクションで記述されています）が、その後の研究は完全に時間がないために停止しました（独自のプロジェクトでの雇用）。 それにも関わらず、読者にはいくつかの考えが興味深いと思われ、この方向でさらなる研究ができると期待して、ここで説明します。
このモデルは、AIのプロトタイプを作成するふりをしないことをすぐに言わなければなりません。 むしろ、自己組織化の可能性と、「利己的」（恒常性）ニューロンの動的システムにおける全体的で意図的な行動の出現の可能性を探求したかったのです。
モデルのロジックをより完全に理解するには、
機能システムの
理論に関する私のトピックを読むのが役立つと思われますが、これもあなたの裁量です。
行こう！
生物学的根拠
このモデルは、機能システムP.Kの理論に基づいて構築されました。 アノヒンとホメオスタシスの理論。
ホメオスタシス -自己調節、動的なバランスを維持することを目的とした協調的な反応を通じて、内部状態の恒常性を維持するオープンシステムの能力。 元々この用語を作り出したウォルター・キャノンは、ホメオスタシスを「身体の知恵」と呼んでいました[1]。
最も単純な生物学的動機は、対応する生理学的ゾーンのニューロンで恒常性平衡が乱れたときに発生します（エネルギー、酸素、または浸透圧の不均衡の違反）。 しかし、生物学的動機付けを評価するための普遍的な単位があります[2]。 このユニットの存在は、モチベーションの満足が喜びを引き起こし、それに応じてこのモチベーションを生成する恒常性システムの不均衡を取り除くという事実によるものです。 したがって、ホメオスタシスのモデリングは、やる気のある人工的なシステムを作成するための直接的な道です。 独自の目標とそれを達成する方法を備えたシステム。 ホメオスタシスシステムにミスマッチをもたらす多くの要因があり、細胞生存のための重要性の観点から、そのような要因の階層があります。 より高いレベルの因子を安定した範囲に維持するために、ホメオスタシスはより低いレベルの因子の調節の最適レベルを修正します。 つまり 関数の回復は、歪んだパラメーターを通常の状態に戻すことではなく、これらのパラメーター間の比率を変更することで迂回的に行われます。 特に、過剰な興奮はニューロンを損傷しますが、恒常性を回復するいくつかの要因があります（cAMP、インターロイキン-1、甲状腺刺激ホルモン放出ホルモンなど）。 したがって、代償性恒常性は、中間段階で、新しい平衡点を見つける途中でニューロンを興奮させることができます。 図 1.ニューロンの2レベルの恒常性のスキームが示されています。 図の赤は条件付きでニューロンへの損傷を示し、緑は修復を示します。 損傷は、ミスマッチを引き起こす外部要因です。
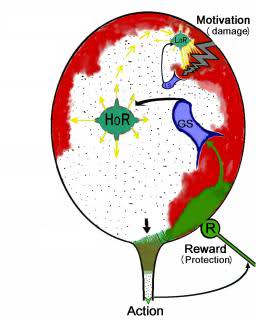図 1.ニューロンの恒常性
（LoR-低レベルの恒常性、HoR-高レベルの恒常性、LS-ローカル不整合センサー、R-不整合レベルを低減する賞）恒常性の一連のモデルは文献[3,4]で知られていますが、それらはニューラルネットワークの自己組織化と意図的な行動に向けられていません。 ニューラルネットワークと強化学習に基づくなど、ターゲットを絞った行動のモデリングにも豊富な歴史があり、文献で広く報告されています。 ただし、これらのモデルの枠組み内では、ニューロンおよびネットワーク全体の恒常性は考慮されませんでした。
実際、上記に基づいて、完全なシステムを構成するモデルの階層が作成されました。
-既知のモデルの重要な特性と問題のパラダイムの基本原理を組み合わせた恒常性ニューロンのモデル。
-恒常性ニューロンに基づく恒常性ニューラルネットワークのモデル。
-恒常性ニューラルネットワークと環境との相互作用によって制御される単純な生物のモデル。
-変化する外部環境における単純な生物の進化的発達のモデリング。
恒常性ニューロンとニューラルネットワークのモデル
主なタスクは、恒常性ニューロンのパラダイムを、ニューラルネットワークの自己組織化のメカニズムおよび自律的な行動への能力の可能な基礎として分析することであるため、この主要な主要モデルに特別な注意を払う必要があります。 恒常性ニューロンのモデルは、各ニューロンがその最適な内部状態-恒常性を維持しようとしていることを意味し、現在の状態が最適な場合、ニューロンは最適な状態に戻ることを目的とした応答を形成します。 すでに述べたように、多くの要因の変化はニューロンの不均衡につながる可能性がありますが、モデルの状況で
は、ニューロンq（t）の状態の統一された
内因性評価を導入し
ます 。 また、
x（t）信号を生成し、自身の活動の恒常性を維持する際のニューロンの能力を反映する
内部エネルギーe（t）の値のインジケーターを導入します。
ニューロンのホメオスタシスへの欲求は、不一致
q opt -q（t）を排除することを目的とした活動で表され、より顕著になるほど、不一致が大きくなります。 ニューロンの活動にはエネルギーコストが必要であるため、利用可能なエネルギーの量
e（t）に応じてさまざまな形をとることができます。
したがって、「エゴイスティック」ニューロンのモデルの要件をいくつか策定しました。 1つの目標を持つそのようなニューロンの-最適に近い状態を維持すること。 ただし、各ニューロンは孤立して存在することはできませんが、完全なニューラルネットワークで機能する必要があります。 したがって、ネットワークの残りから特定のニューロンに対する作用ベクトルの概念を導入できます。
この効果は、次のタイムステップのニューロンの内因性評価を変更します。
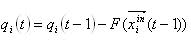
この関数は異なって見えるかもしれませんが、その最も単純なケースは
上記では、ニューロンのすべての特性と、他のニューロンからのニューロンへの影響を決定する方法論を紹介しました。 ここ
で、ニューロンg（t）の
不一致の概念、すでに触れた意味、およびニューロンの動作と出力信号の概念を紹介します。 ニューロンの不一致：
ここで、現在の不一致に基づいて選択
するニューロンの
アクションを定義します。
この段階では、一方ではモデル全体の重要な要素の1つであり、もう一方ではアクションの概念そのものがいくつかの生物学的原理と上記の私たちの考えを蓄積するため、より詳細に説明する必要があります。
最初に注意することは、他のニューロンによるニューロンへの任意のアクションは、恒常性平衡からの逸脱につながることです。 したがって、私たちの「利己的な」ニューロンのすべての行動は、このバランスに戻ることを目的とすべきです。 これが
低レベルの恒常性の原理です 。 アクションの機能をコンパイルするときに実際に考慮されたいくつかの可能なケースがあります。
ニューロンの作用は、主にその矛盾の程度に依存します。 ニューロンが恒常性平衡点から遠く離れている場合、ニューロンはすぐに平衡状態に戻すアクション（スパイク生成）を実行します。 それが平衡に近い場合、恒常性の別のメカニズムが活性化されます-遅い回復。 各アクションに対して、ニューロンはエネルギーを消費します。スパイクでは-大きく、回復では-それほど大きくありません。 ニューロンのエネルギーの補充について以下に説明します。
これに加えて、ニューロンのエネルギーは、必要な場合でもスパイクを生成するのに十分ではない場合があります。これは、エネルギーが補充される瞬間まで回復の選択を意味します。
したがって、ニューロンの作用は、入力信号、状態の内因性評価、およびエネルギー貯蔵の関数です。 実際、これにより、ニューロン（低レベルの恒常性を含む）およびネットワーク全体の正式なモデルが終了します。 図 図2は「利己的な」ニューロンの模式図です。
図 2.「セルフィッシュ」ニューロン生物モデル
ニューラルネットワークは生物全体の一部ですが、完全に定義するには、さらにいくつかの概念を導入する必要があります。 これらの最初は
共通のエネルギープールE（t）で 、そこからネットワーク内のすべてのニューロンのエネルギーが復元されます。
e（t）<e min （最適なニューロンエネルギー供給）の場合、
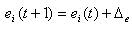
ここで
、トップレベルの恒常性の概念を定義する必要があります。
ネットワーク全体の状態の内生評価の概念を紹介します。
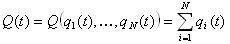
この場合、いくつかの最適な状態
Q optがあると仮定し
ます 。
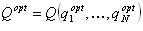
次に、2つの異なるケースで最高レベルの恒常性が有効になることを確認します。
-安定性が確立された後（ネットワークで周期的なプロセスが観察されたが、状態が最適値に達していない場合）
-「必要性」がある場合（ネットワーク状態の内生評価の大きな不一致の場合）
この場合、パラメーター
q i optはランダムに変化しますが、各値の変化の大きさは、ネットワークの状態の内因性評価の不一致と特定のニューロンの内因性評価の不一致の両方に比例します。 したがって、システムが最適な状態に到達できず、ネットワーク全体の寿命が脅かされている場合、最高レベルの恒常性のメカニズムがアクティブになります。 概略的に、そのような生物モデルは図に示されています。 3。
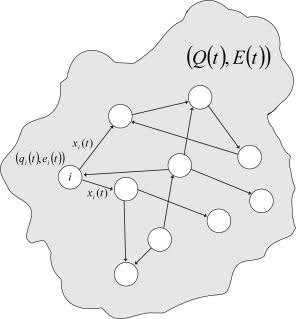図 3.生物のモデルここでは、おそらく、そのようなモデルの定性的なダイナミクスを判断するためのいくつかの実験データを提供する必要があります（トップレベルの恒常性なし）。
W ij〜N （0,1）の分布に従ってランダムに分散された重みと、状態およびエネルギー貯蔵の内生評価のさまざまな最適値を使用して、10個のニューロンのネットワークをコンパイルしました。 さらに、初期化の時点で、9つのニューロンが平衡状態にあり、ニューロンの1つが不一致でした。 図 図4-5は、このようなシステムの各ニューロンの状態とエネルギーの内生評価の時間依存性を示しています。
図 4.ニューロンの状態の内因性評価のダイナミクスのグラフ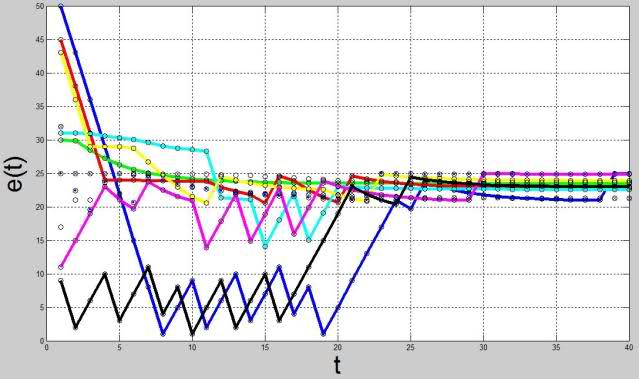
図 5.ニューロンのエネルギー貯蔵のダイナミクスのグラフ結果として、システム全体が恒常性平衡の位置にくることが示されていますが、我々の実験では、恒常性平衡の達成が不可能であり、システム内で自励振動プロセスが開始される一連のパラメーターがあり、より高いレベルの恒常性を可能にする必要があることを示しています。
環境との相互作用
そのような生物を環境に入れたと想像してください。 私たちの体に必要なものはたった1つであると仮定します-恒常性と代謝プロセスに費やされる十分なレベルの総エネルギーを維持する必要があります。 この場合、体がエネルギーレベルを補充するために適切なタイミングで決定を下すことができることが必要です。 それは、例えば、食べ物を彼に提供するためにボタンを押すことです。
身体のマクロパラメーターを導入し、その変化がニーズを決定する（複数ある場合もある）ことを考え、また、身体が環境との相互作用を通じてマクロパラメーターの値を変更できるようにする一連のエフェクターを検討することを考えました。 この問題に対する提案されたアプローチは、マクロパラメータの値に関する情報を恒常性ニューロンに直接転送することに基づいており、ニューロンの内部恒常性を対応するニーズの満足度と結び付けます。 したがって、第2レベルのホメオスタシスはシステム全体のパフォーマンスに責任を負い、第1レベルは環境と相互作用する際の生物の行動の効果的なラインに責任を負います。
例で説明します。 これを行うために、2つの特殊なニューロンがニューラルネットワークの構造に存在すると仮定します。
最初のニューロンはエネルギー補充の必要性に特化しています。つまり、総エネルギーのレベルが不十分な場合は、ミスマッチになります。 つまり、彼は追加の入力を持ち、これは総エネルギー不足（
EE min ）のレベルを受け取ります。 2番目のニューロンは、エネルギー補充アクションの実行に関して特化されています。つまり、スパイクが生成された時点で、外部エネルギーから全エネルギーが補充されます。 このシステムを図に示します。 6。
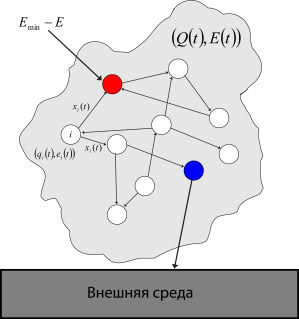図 6.身体と環境との相互作用
赤いニューロンはエネルギー補充の必要性に特化しており、青いニューロンはエネルギー補充アクションのパフォーマンスに特化しています）したがって、身体の不一致は、彼が食物の必要性を感じる瞬間に導入されます。 次に、ニューロンはこのミスマッチを排除しようとします。 アクションの実行に特化したニューロンにスパイクが発生するまで、エネルギーの補充は行われず、エネルギー不足の信号がシステムに流れ続けます。 したがって、ある時点で、2番目の特殊なニューロンでスパイクが生成され、総エネルギー供給が補充されます。そのため、エネルギー補充の必要性に特化したニューロンが不整合になります。
もちろん、これは非常にモデル的な状況ですが、そのような生物がどのようなロジックで機能するかは、何らかの決定が必要な環境で機能することを示しています。
連続モデル
この時間離散モデルを連続させる方法を考える人のためだけに、ニューロンのFitzHugh-Nagumoモデルに基づいたバージョンを引用します。
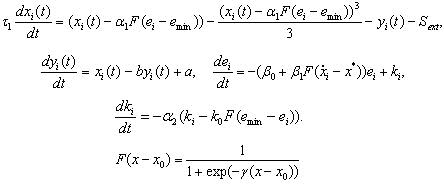
おわりに
もちろん、このモデルは少なくともある程度の完全性を主張することはできません。 しかし、私はそれに埋め込まれた思考のいくつかは非常に興味深いものであり、読者による研究の主題になり得るように思えます。 特に、アクションを実行する動機としてのニューロンの不一致の考え方、微小環境とニューロンの内部パラメーターの比としての不一致の定義、および不一致を排除するためおよび自己組織化効果のための基礎としての恒常性。
また、このトピックでは、かなり単純なモデルであっても、自己組織化の興味深い効果が生じ、長期的には全体的な行動につながる可能性があるという事実に読者の注意を引きたいと思いました。
このレビューでは、このモデルに学習プロセスを導入するという些細な問題や、進化そのものには触れなかったことに注意してください。 これらはすべて、さらに可能な研究の対象となっています。
著者
Maxim Komarov（ニジニノヴゴロド大学）、Daniil Kanevsky（VMiK MSU）、Sergey Kulivets（IPU RAS）、および謙虚な使用人がこのモデルの開発に参加しました。 レフ・エフィモヴィチ・チシロフスキー（イスラエル、バーイラン大学、イスラエル）とウラジミール・ゲオルギエヴィチ・レドコ（NIISI RAS）は、私たちが漂流していたときの彼らの支援と私たちの思考の方向の追跡に感謝します。 私たちはそれぞれ、このモデルに、私たちが従事している分野からの考えと考慮事項をもたらしました。
参照資料
[1] 。 Cannon WB Physical Review、1928、9：399-431。
[2] 。 Cabanac M. Journal of Theoretical Biology、1992、155：173-200。
[3] 。 Davis GW Annual Review of Neuroscience、29：307-323、2006。
[4] 。 Marder A.、Prinz AA BioEssays、24：1145-1154、2002