こんにちは、Habrahabr。 これは、私のプログラムのフレームワークの別の投稿で、最大のITリソースのデータベースをアルゴリズムとデータ構造に関する情報で強化します。 実践が示すように、この情報は多くの人にとって十分ではなく、プログラミングライフのさまざまな分野で必要とされています。
理解しやすく、多くのコードを必要としないアルゴリズム/構造を主に選択し続けますが、実用的な価値を過小評価することは困難です。 前回は
デカルトの木でした。 今回
は、素集合のシステムです 。
ディスジョイントセットユニオン (DSU)または
Union-Findとも呼ばれ
ます 。
状態
次のタスクを設定します。
Nタイプの要素を操作しましょう(簡単にするため、以下では0からN-1までの数字)。 数のグループはセットに結合されます。 構造に新しい要素を追加して、それ自体からサイズ1のセットを形成することもできます。 最後に、定期的にいくつかの2つのセットを1つにマージする必要があります。
タスクを形式化します。次の操作をサポートする
高速構造を作成します。
MakeSet(X) -構造体に新しいX要素を導入し、サイズ1のセットをそれ自体から作成します。
Find(X) -要素Xが属するセットの
識別子を返します
識別子として、このセットから要素を1つ選択します-セットの
代表です 。 同じセットに対して、代表が同じものを返すことが保証されます。そうでない場合、構造を操作することはできません:(
if (Find(X) == Find(Y))が正しくない
if (Find(X) == Find(Y)) 2つの要素が同じセットに属している
if (Find(X) == Find(Y))チェック
if (Find(X) == Find(Y))こともできます。
Unite(X、Y) -要素XとYが1つの新しいセットにある2つのセットを結合します。
図では、このような仮想構造の動作を示します。
実装
古典的なDSUの実装は、1964年に
バーナードギャラーと
マイケルフィッシャーによって提案されましたが、すでに1975年に
ロバートタリアンによって調査されました(複雑さの一時的な評価を含む)。タリアンもいくつかの結果、改善、アプリケーションを所有しています。
データ構造をフォレストの形式で保存します。つまり、DSUを独立したツリーのシステムに変換します。 1つのセットのすべての要素は1つの対応するツリーにあり、ツリーの代表はそのルートであり、セットのマージは2つのツリーを1つに結合したものです。 これからわかるように、このようなアイデアは、2つの小さなヒューリスティックと相まって、結果として生じる構造の驚くほど高速につながります。
まず、ツリーの各頂点にその直接の祖先(およびツリーXのルート自体)を格納する配列
pが必要です。 この配列のみを使用すると、最初の2つのDSU操作を効果的に実装できます。
MakeSet(X)
要素Xから新しいツリーを作成するには、それが自身のツリーのルートであり、祖先がないことを示すだけで十分です。
public void MakeSet(int x) { p[x] = x; }
検索(X)
ツリーの代表はそのルートと見なされます。 次に、この代表を見つけるには、ルートにつまずくまで親リンクを上回れば十分です。
しかし、これがすべてではありません。縮退した(インラインに拡張された)ツリーの場合のこのような単純な実装は、O(N)で機能しますが、これは受け入れられません。 検索を高速化することができます。 たとえば、直接の祖先だけでなく、対数の大きなテーブルを格納するには、大量のメモリが必要です。 または、祖先にリンクする代わりに、ルート自体へのリンクを保存します-ただし、ツリーを結合する場合(Unite)、ツリーの1つの要素はすべてこれらのリンクを変更する必要がありますが、これもO(N)のオーダーの時間消費です。
他の方法を使用します。実装を高速化する代わりに、ツリー内の過度に長いブランチを防ぐようにします。 これは最初のDSUヒューリスティックであり、パス圧縮と呼ばれます。 ヒューリスティックの本質:代表がまだ見つかった後、Xからルートまでのパスに沿った各頂点について、先祖をこの代表に変更します。 つまり、実際には、ルートへの長い分岐の代わりに、これらすべての頂点を再サスペンドします。 したがって、検索操作の実装は2パスになります。
この図は、検索(3)操作の前後のツリーを示しています。 赤いrib骨-ルートへのパスに沿って歩いたthose骨。 今、それらはリダイレクトされます。 その後、木の高さが劇的に減少したことに注目してください。
ソースコードを再帰的な形式で記述するのは非常に簡単です。
public int Find(int x) { if (p[x] == x) return x; return p[x] = Find(p[x]); }
結合(X、Y)
2つのツリーの合併により、少し工夫が加えられました。 最初に、すでに記述されているFind関数を使用して、両方のマージツリーのルートを検索します。 さて、実装はツリーをマージするために直接の親への参照のみを保存することを思い出して、息子のルートの1つ(およびツリー全体)を他の子に中断するだけで十分です。 したがって、このツリーのすべての要素は自動的に別の要素に属します-代表者の検索手順は、新しいツリーのルートを返します。
問題は次のとおりです。どのツリーにぶら下げるか。 たとえば、ツリーXのように常に1つを選択するのは良くありません。N個のユニオンの後、縮退ツリー(N要素の1つのブランチ)を取得する例を見つけるのは簡単です。 そして、木の高さを減らすことを目的とした2番目のDSUヒューリスティックがあります。
先祖に加えて、別の
ランク配列を保存します。 その中には、各ツリーに対して、その高さの上限、つまりその中の最長のブランチが保存されます。 それは高さそのものではないことに注意してください-Findを実行する過程で、最長のブランチは自己破壊する可能性があり、新しい最長のブランチを見つけるためにさらに多くの反復を費やすことはあまりにも高価です。 したがって、ランク配列の各ルートには、そのツリーの高さ以上であることが保証された数値が書き込まれます。
マージの決定は簡単になりました。DSUで長すぎるブランチを防ぐために、下位のツリーを上位のツリーからぶら下げます。 それらの高さが等しい場合-誰から誰を掛けるかは関係ありません。 しかし、後者の場合、新しく作成されたルートはランクを上げることを忘れてはなりません。
これは、典型的なUniteがどのように生成されるかです(たとえば、パラメーター8と19で):
public void Unite(int x, int y) { x = Find(x); y = Find(y); if (rank[x] < rank[y]) p[x] = y; else { p[y] = x; if (rank[x] == rank[y]) ++rank[x]; } }
ただし、実際には、ランクの詐欺に追加のO(N)メモリを費やすことはできません。 再懸濁のルートを
ランダムに選択するだけで十分です-驚くべきことに、このソリューションは、実際には元のランキングの実装と非常に匹敵する速度を提供します。 この記事の著者は、生涯にわたってランダム化DSUを使用してきましたが、失敗することは一度もありませんでした。
C#実装:
public void Unite(int x, int y) { x = Find(x); y = Find(y); if (rand.Next() % 2 == 0) Swap(ref x, ref y); p[x] = y; }
性能
2つのヒューリスティックの使用により、各操作の速度はツリーの構造と、以前に実行された操作のリストのツリーの構造に大きく依存します。 唯一の例外はMakeSetです-その動作時間は明らかにO(1)です:-)他の2つの場合、速度は非常に明白です。
Robert Taryanは1975年に注目すべき事実を証明しました。サイズNのフォレストでのFindとUniteの両方の操作時間はO(α(N))です。
数学のα(N)の下には、逆アッカーマン関数、つまり
f(N)= A(N、N)の逆関数があります。
アッカーマンの関数 A(N、M)は、巨大な成長率を持つことが知られています。 たとえば、
A(4、4)= 2 2 2 65536 -3の場合、この数値は非常に大きくなります。 一般に、考えられるすべてのNの実用的な値に対して、その逆アッカーマン関数は5を超えません。したがって、それを定数として取り、
O(α(N))≅O(1)と仮定できます。
だから私たちは持っています:
MakeSet(X)-O(1)。
検索(X)-O(1)は償却されます。
結合(X、Y)-O(1)償却済み。
メモリ消費-O(N)。
全然悪くない:-)
実用的なアプリケーション
DSUにはさまざまな用途があります。 それらのほとんどは、
オフラインで問題を解決することに関連しています。つまり、プログラムが受け取る構造に関するクエリのリストが事前にわかっている場合です。 ここでは、これらのタスクのいくつかと、ソリューションの簡単なアイデアを示します。
最小重量のスケルトン
重み付きエッジを持つ無向接続グラフが与えられます。 結果としてツリーを取得し、このツリーのエッジの総重量が最小になるように、そこからいくつかのエッジをスローします。
このタスクが発生する既知の場所の1つは(異なる方法で解決されますが)、イーサネットネットワーク内の冗長接続をブロックして、起こり得るパケットサイクルを回避することです。 この目的のために作成されたプロトコルは広く知られており、主要な変更の半分がシスコによって行われています。 詳細については、
スパニングツリープロトコルを参照してください。
この図は、最小スケルトンが強調表示された重み付きグラフを示しています。
この問題を解決するためのクラスカルのアルゴリズム:すべてのエッジを重みの昇順でソートし、DSUを使用して現在の最小重みのフォレストを維持します。 最初に、DSUはN個のツリーで構成され、それぞれに1つの頂点があります。 rib骨に沿って昇順に行きます。 現在のエッジが異なるコンポーネントを結合している場合、それらを1つにマージし、コアの要素としてエッジを記憶します。 コンポーネントの数が1に達するとすぐに、目的のツリーを構築しました。
TarjanのLCAオフライン検索アルゴリズム
ツリーと次の形式のクエリのセットを指定します。指定された頂点
uおよび
vについて 、最も近い共通の祖先(最小共通の祖先、LCA)を返します。 クエリのセット全体は事前にわかっています。 タスクはオフラインで作成されます。
ツリーを深く検索することから始めましょう。 クエリ<u、v>を検討してください。 深さの検索を、要求頂点の1つ(たとえばu)が以前に検索で既に訪れていて、検索の現在の頂点がvであり、サブツリーv全体がちょうど調べられた状態にします。 明らかに、要求に対する応答は、頂点v自体またはその祖先のいずれかです。 さらに、ルートへのパスに沿った各祖先vは、それが答えである頂点uの特定のクラスを生成します。このクラスは、そのような祖先の「左側の」既に表示されたツリーブランチとまったく同じです。
図では、頂点がクラスに分割されたツリーを見ることができますが、白い頂点はまだ表示されていません。
このような頂点のクラスは交差しません。つまり、それらはDSUでサポートされます。 深さ検索がサブツリーから戻るとすぐに、このサブツリーのクラスを現在の頂点のクラスとマージします。 そして、答えを探すために、
祖先配列をサポートします-各頂点に対して、この頂点のクラスを生成した祖先の固有者。 代表のこの配列のセル値は、ツリーをマージするときに書き換えを忘れてはなりません。 しかし、今では、完全に処理された各頂点vを詳細に検索するプロセスで、クエリリストですべての<u、v>を見つけることができます。ここで、uは既に処理され、答えを出力します:
Ancestor[Find(u)] 。
マルチグラフの接続コンポーネント
マルチグラフ(頂点のペアが複数の直接エッジで接続できるグラフ)が与えられ、「いくつかのエッジを削除」および「グラフに現在接続されているコンポーネントの数」という形式のクエリが受信されます。クエリのリスト全体が事前にわかっています。
解決策はささいなことです。 まず、すべての削除リクエストを実行し、最終的なグラフのコンポーネント数を計算して、それを記憶します。 結果のグラフをDSUにプッシュします。 ここで、逆の順序で削除要求に進みます。古いグラフからの各エッジの削除は、DSUに格納された「フラッシュバックグラフ」の2つのコンポーネントのマージの
可能性を意味します。 この場合、現在接続されているコンポーネントの数は1つ減少します。
画像のセグメンテーション
画像を考えてみましょう-ピクセルの長方形の配列。 グリッドグラフとして表すことができます。各頂点ピクセルは、4つの最も近い隣接するエッジで直接接続されています。 タスクは、たとえば同じ色の画像内の同じセマンティックゾーンを強調表示し、2つのピクセルが同じゾーンにあるかどうかをすばやく判断できるようにすることです。 たとえば、古い白黒のフィルムはペイントされます。まず、グレーの色調がほぼ同じ領域を選択する必要があります。
この問題を解決するには2つの方法があり、どちらもDSUを使用します。 最初のオプションでは、隣接するピクセルの各ペア間ではなく、色が十分近いピクセル間にのみエッジを描画します。 その後、グラフの通常の長方形の走査がDSUを埋め、接続されたコンポーネントのセットを取得します-それらは同じ色の画像領域です。
2番目のオプションはより柔軟です。 rib骨を完全に削除するわけではありませんが、それぞれのcolor骨に、色の違いやその他の追加の要因に基づいて計算された重みを割り当てます-特定の各セグメンテーションタスクに固有です。 得られたグラフでは、たとえば同じクラスカルアルゴリズムを使用して、最小の重みのフォレストを見つけるだけで十分です。 実際には、現在の接続エッジがDSUに記録されるのではなく、現時点で2つのコンポーネントが別の特別な重み関数の標準によってあまり変わらないもののみが記録されます。
ラビリンスジェネレーション
タスク:1つの入力と1つの出力を持つ迷路を生成します。
ソリューションアルゴリズム:
入り口と出口を除くすべての壁が設置された状態から始めましょう。
アルゴリズムの各ステップで、ランダムな壁を選択します。 間にあるセルがまだ接続されていない場合(DSUの異なるコンポーネントにある場合)、それを破棄します(コンポーネントをマージします)。
特定の収束状態までプロセスを続行します。たとえば、入力と出力が接続されている場合などです。 または、1つのコンポーネントが残っている場合。
シングルパスアルゴリズム
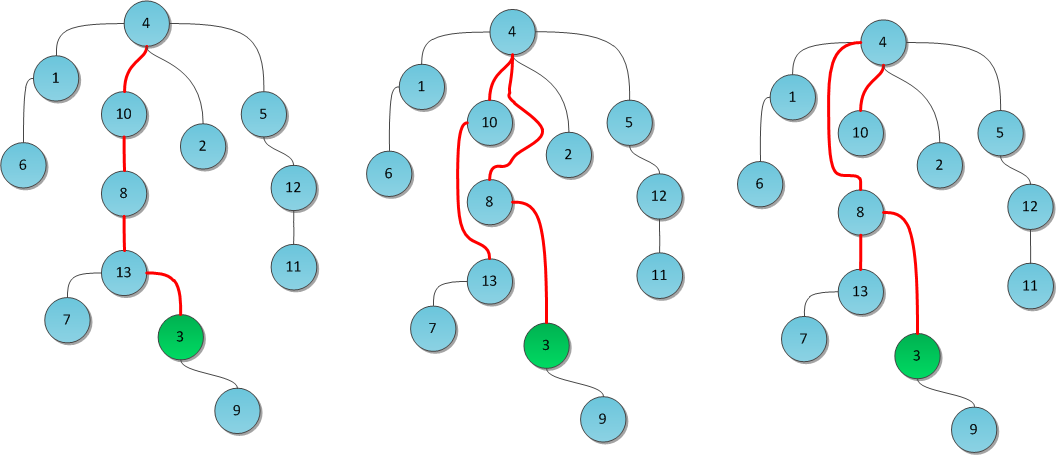
Find(X)には、2つではなく1つのルートへのパスを必要とするが、同じまたはほぼ同じ程度のパフォーマンスを保持する実装オプションがあります。 それらは、パス圧縮とは対照的に、ツリーの高さを減らすための他の戦略を実装します。
オプション#1:
パス分割 。 上位Xからルートへの途中で、各頂点の親接続を祖先から祖先(祖父)の祖先にリダイレクトします。
オプション番号2:
パスの半分 。 ただし、パス分割の考え方を取り入れて、パスに沿ったすべての頂点の接続ではなく、リダイレクト先の接続のみ、つまり「祖父」の接続をリダイレクトします。
図では同じツリーが使用され、検索(3)クエリが実行されます。 中央では、結果は右側のパス分割を使用して表示されます-パスは半分になります。
機能実装
ばらばらのセットのシステムには1つの大きな欠点があります。それは、命令型スタイルで実装されるため、どのような形式でもUndo操作をサポートしません。 各操作がその場で構造を変更せず、必要な変更が行われたわずかに変更された新しい構造を返す場合、機能スタイルのDSUを実装する方がはるかに便利です(古い構造と新しい構造のメモリのほとんどは共通です)。 このようなデータ構造は、英語の用語では
永続と呼ばれ、データの不変性の概念が支配する純粋な関数型プログラミングで広く使用されています。
DSUアルゴリズムの純粋に必須のアイデアのため、その機能の実装は、パフォーマンスを維持しながら、長い間考えられないように思われました。 しかし、2007年に、Sylvain ConchonとJean-ChristopheFilliâtreは、彼らの研究で、Unite操作が変更された構造を返す必要な機能的変形を提示しました。 正直に言うと、完全に機能しているわけではなく、命令型の割り当てを使用していますが、実装内に安全に隠されており、永続的なDSUインターフェイスは純粋に機能しています。
実装の主なアイデアは、「永続配列」を実装するデータ構造の使用です。これらは、配列と同じ操作をサポートしますが、メモリを変更せず、変更された構造を返します。 このような配列は、何らかのツリーを使用して簡単に実装できますが、この場合、それを使用した操作にはO(log
2 N)時間かかり、DSUの場合、そのような推定はすでに過度に大きくなります。
技術的な詳細については、読者は
元の記事を参照して
ください 。
文学
この記事の範囲内の互いに素な集合のシステムは、有名な本-Kormen、Leiserson、Rivest、Stein "Algorithms:construction and analysis。"で議論されています。 また、操作の実行に約α(N)時間かかるという証拠もあります。
Maxim Ivanovの
サイトで 、C ++でのDSUの完全な実装を見つけることができます。
Union-Find Problemの
待機フリー並列アルゴリズムの記事では、DSU実装の並列バージョンについて説明しています。 スレッドロックはありません。
ご清聴ありがとうございました:-)