Antアルゴリズム

まえがき

ごく最近、ミツバチの群れの行動に関する記事がこのブログに掲載されました。 この記事では、 antアルゴリズムと呼ばれる別の群知能アルゴリズムについて説明します 。 それは、借用された自然メカニズムについて簡単に説明する紹介、元のマルコドリゴアルゴリズムの説明、他のアリアルゴリズムのレビュー、およびアリアルゴリズムの応用分野と彼らの研究の有望な方向を示す結論から成ります。

はじめに

アリをスマートと呼ぶことはできません。 単一のアリはわずかな決定を下すことはできません。 事実は、それが非常に原始的に配置されているということです。そのすべての動作は、環境と兄弟の反応に対する基本的な反応に帰着します。 アリは、分析し、結論を導き、解決策を探すことができません。

ただし、これらの事実は、種としてのアリの成功とは決して一致しません。 彼らは地球上に1億年以上存在し、巨大な住居を建て、必要なものすべてを提供し、実際の戦争さえ行います。 個々の個人の完全な無力さに比べて、アリの成果は考えられないように見えます。

アリは彼らの社会性のためにそのような成功を達成することができます。 彼らは集団にのみ住んでいます-コロニー。 コロニーのすべてのアリは、いわゆる群知能を形成します。 コロニーを構成する個人は賢くてはいけません。彼らは特定の-非常にシンプルな-ルールに従ってのみ相互作用するべきであり、それからコロニーは完全に効果的です。

植民地には支配的な人物、上司や部下、指示を与えたり行動を調整したりするリーダーはいません。 コロニーは完全に自己組織化されています。 アリのそれぞれは、地元の状況に関する情報のみを持ち、その全体が状況全体についての考えを持っている人はいません。彼自身または親relativeから、明示的または暗黙的に学んだことについてのみです。 スティグメルジアと呼ばれるアリの暗黙の相互作用は、アリ​​の丘から食料源までの最短経路を見つけるメカニズムに基づいています。

アリは、蟻塚から餌に戻ったり、戻ったりするたびに、フェロモンの道を後にします。 地球上にそのような痕跡を感じた他のアリは、本能的にそれに向かって駆け寄るでしょう。 これらのアリはフェロモンのパスも背後に残すため、特定のパスに沿って進むほど、アリは親relativeにとって魅力的になります。 さらに、食物源への経路が短いほど、アリがそれを食べるのにかかる時間が短くなります。したがって、その上に残った痕跡がより早く目立つようになります。

1992年、Marco Dorigoの論文で、記述された最適化問題を解決するための自然なメカニズムを借りることを提案しました[1]。 アリのコロニーの性質を真似て、アリアルゴリズムはマルチエージェントシステムを使用します。このエージェントのエージェントは、非常に単純なルールに従って機能します。 これらは、たとえば巡回セールスマン問題など、このタイプのアルゴリズムを使用して解決される最初の問題など、複雑な組み合わせ問題の解決に非常に効果的です。

巡回セールスマン問題を解決するための古典的なantアルゴリズム

前述のように、antアルゴリズムはマルチエージェントシステムをモデル化します。 彼女のエージェントは将来アリと呼ばれます。 本物のアリのように、彼らは非常に単純です：彼らは彼らの義務を実行するために少量のメモリを必要とし、作業の各ステップで単純な計算を実行します。

各アリは、渡されたノードのリストをメモリに保持します。 このリストは、タブーリストまたは単にant メモリと呼ばれます 。 次のステップでノードを選択すると、アリはすでに通過したノードを「記憶」しており、移行の可能性があるとは見なしません。 各ステップで、禁止リストは新しいノードで補充され、アルゴリズムの新しい反復の前、つまりアリが再びパスを通過する前に空になります。

禁止のリストに加えて、遷移のノードを選択するとき、アリは、通過できるrib骨の「魅力」に導かれます。 それは、最初にノード間の距離（つまり、rib骨の重量）に依存し、2番目に、以前に通過したアリがエッジに残したフェロモンの痕跡に依存します。 当然のことながら、一定のエッジの重みとは対照的に、フェロモンの痕跡はアルゴリズムの各反復で更新されます。自然のように、痕跡は時間とともに蒸発し、反対にアリを通過させると、それらを強化します。

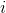
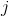
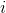
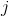
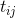
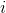
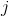
アリを結び目にしましょう 、およびノー​​ド -これは、移行に使用できるノードの1つです。 。 ノードを接続するエッジの重みを示します そして のような フェロモン強度は 。 次に、アリの遷移の確率 で に等しくなります：



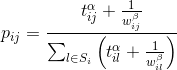
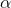
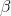
どこで そして -これらは、パスを選択する際のコンポーネントの重要度（リブ重量とフェロモンレベル）を決定する調整可能なパラメーターです。 明らかに、 アルゴリズムが古典的な欲張りアルゴリズムに変わり、 彼はある最適以下のソリューションにすぐに収束します。 パラメータの正しい比率の選択は研究の主題であり、一般的な場合、経験に基づいています。

アリが正常にルートを通過した後、通過したすべてのエッジに、移動したパスの長さに反比例する軌跡を残します。

、

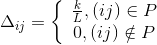
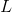
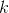
どこで -パスの長さ、および -調整可能なパラメーター。 さらに、フェロモントレースが蒸発します。つまり、アルゴリズムの各反復で、すべてのエッジのフェロモン強度が減少します。 したがって、各反復の終わりに、強度を更新する必要があります。

古典的なアルゴリズムの修正のレビュー

巡回セールスマンの問題を解決するためにantアルゴリズムを使用した最初の実験の結果は有望でしたが、既存の方法と比較して最良とはほど遠いものでした。 しかし、古典的なantアルゴリズム（「antシステム」と呼ばれる）の単純さは改善の余地を残しました。マルコドリゴおよびその他の組み合わせ最適化の分野の専門家によるさらなる研究の対象となったのはアルゴリズムの改善でした。 基本的に、これらの改善は、検索履歴のより多くの使用と、すでに見つかった成功したソリューションの周辺領域のより徹底的な研究に関連しています。 以下は、最も注目に値する変更点です。

エリートアリシステム

これらの改良点の1つは、いわゆる「エリートアリ」のアルゴリズムへの導入です。 経験から、短いパスに入るrib骨を通過するとき、アリはさらに短いパスを見つける可能性が高いことが示されています。 したがって、効果的な戦略は、最も成功したルートでフェロモンのレベルを人為的に増やすことです。 これを行うには、アルゴリズムの各反復で、各エリートアリが道を行きます。これは、現時点で見つかったアリの中で最も短いものです。

実験は、一定レベルまで、エリートアリの数の増加が非常に効果的であり、アルゴリズムの反復回数を大幅に削減することを示しています。 ただし、エリートアリの数が多すぎる場合、アルゴリズムはすぐに最適でないソリューションを見つけて、その中に閉じ込められます[3]。 他の変数パラメーターと同様に、エリートアリの最適な数は経験的に決定する必要があります。

Ant-q

Luca M. GambardellaとMarco Dorigoは1995年に、antアルゴリズムを発表した作品を発表しました。これは、機械学習法Qラーニング[4]との類推でその名前を得ました。 このアルゴリズムは、antシステムを強化学習システムとして解釈できるという考えに基づいています。 Ant-Qは、Qラーニングから多くのアイデアを借用することで、この類推を強化しています。

アルゴリズムは、各エッジと、このエッジに沿った遷移の「有用性」を決定する値と一致するQテーブルを保存します。 このテーブルは、アルゴリズムの操作中、つまりシステムのトレーニング中に変更されます。 エッジ遷移ユーティリティの値は、可能な次の状態の予備決定の結果として、次のエッジに沿った遷移ユーティリティの値に基づいて計算されます。 各反復の後、ユーティリティは対応するエッジを含むパスの長さに基づいて更新されます。

アリコロニーシステム

1997年に、同じ研究者が彼らによって開発されたさらに別のアリアルゴリズムに捧げた論文を発表しました[5]。 従来のアルゴリズムと比較して効率を高めるために、3つの主要な変更が導入されました。

まず、エッジのフェロモンのレベルは、次の反復の最後だけでなく、ノードからノードへのアリの各遷移でも更新されます。 第二に、反復の終わりに、フェロモンのレベルは見つかった最短経路でのみ増加します。 第三に、アルゴリズムは修正された遷移規則を使用します：アリは、ある程度の確率で、フェロモンの長さとレベルに応じて、エッジを確実に選択するか、古典的なアルゴリズムと同じ方法で選択を行います。

Max-min Antシステム

同じ年に、TomasStützleとHolger Hoosは、アリがとる最良の経路でのみフェロモンの濃度の増加が発生するアリアルゴリズムを提案しました[6]。 局所的な最適化へのこのような大きな注意は、エッジ上のフェロモンの最大および最小濃度に対する制限の導入によって補われます。これは、アルゴリズムを時期尚早な収束への早期収束から非常に効果的に保護します。

初期化段階で、すべてのエッジのフェロモンの濃度は最大値に等しく設定されます。 アルゴリズムの各反復の後、1つのアリのみがトレースを残します。この反復で最も成功するか、エリート主義のアルゴリズムのようにエリートのいずれかです。 これは、一方では検索エリアのより徹底的な研究、他方ではその加速を実現します。

アスランク

Bernd Bullnheimer、Richard F. Hartl、ChristineStraußは、各反復の終わりに、アリが移動したパスの長さに従ってランク付けされる古典的なアリアルゴリズムの修正を開発しました[7]。 したがって、ribにアリが残したフェロモンの数は、その位置に比例して割り当てられます。 さらに、すでに見つかった成功したソリューションの近隣のより徹底的な研究のために、アルゴリズムはエリートアリを使用します。

おわりに

巡回セールスマンの問題は、おそらく最も調査された組み合わせ最適化問題です。 アリのコロニーの振る舞いを借用するアプローチを使用してソリューションのために最初に選ばれたのが彼女だったのは驚くことではありません。 その後、このアプローチは、割り当ての問題、グラフの色付けタスク、ルーティングの問題、データマイニングおよびパターン認識領域のタスクなどを含む、他の多くの組み合わせの問題の解決に適用されました。

antアルゴリズムの効率は、一般的なメタヒューリスティック手法の効率に匹敵し、場合によっては問題指向の手法にも匹敵します。 Antアルゴリズムは、検索領域のサイズが大きい問題に対して最良の結果を示します。 Antアルゴリズムはローカル検索手順での使用に適しているため、それらの開始点をすばやく見つけることができます。

この方向でさらに研究するための最も有望な領域は、カスタムアルゴリズムパラメーターを選択する方法の分析と見なされる必要があります。 近年、アルゴリズムのパラメータをオンザフライで適応させるさまざまな方法が提案されています[8]。 antアルゴリズムの動作はパラメーターの選択に大きく依存するため、現時点で研究者の最大の関心が集められているのはまさにこの問題です。

文学

[1] M. Dorigo、「Ottimizzazione、apprendimento automatico、ed algoritmi basati su metafora naturale（最適化、学習、および自然アルゴリズム）」、システムおよび情報電子工学の博士号、Politecnico di Milano、1992 g。

[2] A. Colorni、M。Dorigo、V。Maniezzo、「アリのコロニーによる分散最適化」//人工生命に関する最初のヨーロッパ会議の議事録、パリ、フランス、Elsevier Publishing、pp。134-142、1991

[3] M.ドリゴ、V。マニエッツォ、A。コロニ、「Antシステム：協力エージェントのコロニーによる最適化」// IEEE Transactions on Systems、Man、and Cyber​​netics-Part B、26、1、p.29 -41、1996

[4] LMガンバルデラ、M。ドリゴ、「Ant-Q：巡回セールスマン問題への強化学習アプローチ」//機械学習に関する第12回国際会議、モーガンカウフマン、pp。252-260、1995年。

[5] M.ドリゴ、LMガンバルデラ、アントコロニーシステム：巡回セールスマン問題に対する協調学習アプローチ//進化的計算に関するIEEEトランザクションVol。 1、1、pp。53-66、1997。

[6] T.Stützle、H。Hoos、「MAX-MIN Antシステムと巡回セールスマン問題のローカル検索」// IEEE進化計算に関する国際会議、pp。309-314、1997年。

[7] Bernd Bullnheimer、Richard F. Hartl、ChristineStrauß、「Ant Systemの新しいランクベースのバージョン。 計算研究” //経済学と経営科学における適応情報システムとモデリング、1997年。

[8] T.Stützle、M。López-Ibáñez、P。Pellegrini、M。Maur、M。de Oca、M。Birattari、Michael Maur、M。Dorigo、「パラメーターの適応におけるアントコロニー最適化」//テクニカルレポート、イリディア、Libre de Bruxelles大学、2010