長方形グリッド上のサイクル数をカウントするための動的プログラミング手法

この記事は、プログラミングアルゴリズムに携わっており、特に解決が難しい問題に関心がある読者を対象としています。 Habrにアルゴリズムを配置することに反対するhabralyudaは、すぐにこの作品を読むのをやめるべきです。

記事では、プロファイルに動的計画法を使用して、サイズm x nの長方形格子上のハミルトニアンサイクル数をカウントする問題を解決する方法を示します。 Habréには、動的プログラミングのトピックに関する記事がいくつかありますが（例えば、これ）、メソッドのより複雑なアプリケーションの問題はどこにもありません。この方法は、必要に応じて伝達行列法とも呼ばれます。

記事には約2,000語（A4の8ページ）が含まれていますが、歩く人が道を進むことを警告します。

まとめ

難しいタスクについて少し
問題の定義と説明
スライスとステートマシン
伝達マトリックス法
マトリックスフリーのソリューション
アルゴリズムの複雑さ
モジュラー演算
議論と結果
使用されたソースのリスト

1.難しいタスクについて少し

難しいタスクとは何ですか？これは、効果的な解決アルゴリズムを持たないタスクです。さらに、これは必ずしも解の指数関数的な複雑さの問題ではなく、複雑さは多項式である可能性がありますが、十分に大きな多項式（たとえば、ここですでに書いたkクイーンの問題）です。このような問題とその分類についての詳細は、M。Gary、D。Johnsonによる古典的な本、「コンピューターと解決が難しい問題」に記載されています。

このような問題は通常、ブルートフォース、動的プログラミング、および組み合わせ分析によって解決されます。多くの場合、これら3つのコンポーネントを同時に使用することで許容できるソリューションが得られますが、これにはかなり最適なコードを記述する経験も必要です。少なくとも数千のコアと少なくとも数百ギガバイトのRAMのクラスターが手元にあれば非常に便利です。残念ながら、私は冗談ではありません。多くのタスクはそのようなマシンでしか解決できません...

私は難しい問題を解決するのが好きで、時々このテーマで数学者プログラマーのためのコンテストを開催します。この記事の一部は、2010年10月1日に始まり、10月31日に終了する「プレハミルトニアンサイクル」コンテストに捧げられています。

アルゴリズムの複雑さの導出のセクションでは、読者は組み合わせ論の要素（組み合わせの数など）を知っていると想定され、有限状態マシンのセクションでは、読者はグラフ理論の要素（たとえば、グラフの隣接行列とは何か、学位）。

2.問題の定義と説明

この作業では、長方形格子P _m ×P _nと呼ばれるグラフに遭遇します。長方形格子は、座標平面の整数点であり、最近傍の原理で接続されています。 P _m ×P _nという表記は、整数の長方形が2つのチェーンの直接の積であり、最初のチェーンにはm個のリンク（P _mで表示）、2番目のチェーンにはn（P _nで表示）があるという事実によるものです。数値mはラティスの幅（左から右への長さ）、nはその長さ（下から上への長さ）です。

グラフのハミルトニアンサイクルは、各頂点を1回だけ通過するサイクルです。図図1は、格子P ₆ ×P ₈上のハミルトニアンサイクルの例を示しています。

図1-6×8格子上のハミルトニアンサイクルの例

問題は、与えられたmに対して、n≥2で、格子上のハミルトニアンサイクルの数P _m ×P _nを見つけることです。たとえば、次の図は、4×4格子上の6つのハミルトニアンサイクルすべてを示しています。

図2-4×4格子上の6つのハミルトニアンサイクルすべて

3.カットおよびステートマシン

グラフの任意のサイクルP _m ×P _nは、「レイヤー」P _m ×P _k （k = 0,1,2、...、n）上に連続して構築できます。わかりやすくするために、図図3は、グラフを2つの部分に分割する線を示しています。その下はP ₆ ×P _5のグラフで、未完成の「サイクル」は互いに素なチェーンの集合です。サイクルのこの構成された部分は「過去」と呼ばれます。線の上に、未完成の「サイクル」を完了するための可能なオプションの1つが示されています（これが「未来」です）。サイクルは閉じられ、その変曲点でカットラインに接触しません。そして、サイクルを任意の方向に回って開始点に戻るため、カットラインはサイクルによって偶数回交差します。

図3-サイクルのセクション

サイクル自体とカットラインの交点は、ゼロで放電される通常のブラケットシーケンスとして表すことができます。たとえば、図 3、そのようなシーケンスは（0000）の形式を持っています。このシーケンスでは、一致する開始ブラケットと終了ブラケットのペアが「過去」を通過する同じチェーンの両端に対応し、ゼロはこれらのポイントでカットラインとサイクルの交差がないことを意味します。したがって、 すべての切開は、ゼロで放電される正しいブラケットシーケンスで暗号化できます。最初と最後のセクションはゼロ（完全にゼロで構成される）でなければならないので、それらを区別し、1つを下の行で、2つ目を上の行で示す必要があります。

サイクルを構築するプロセスでは、「過去」または「未来」のいずれかを知る必要はありませんが、特定の瞬間にどのセクションが判明したか、およびこのセクションから残りを取得する方法に関する情報のみを保存すれば十分です。実際、現在のセクションから次のセクションに移動する方法は？たとえば、図のように。 3は、セクション（0000）から次のセクション00（）00への遷移を示します。これは例で示されます。

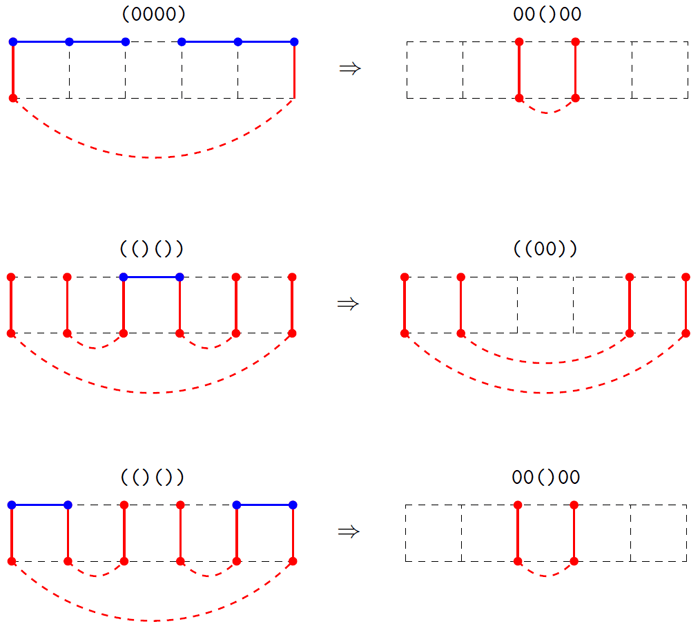図4-あるセクションから別のセクションへの遷移の例

図図4は、1つのセクションから別のセクションへの遷移の3つの例を示しています。円弧線は、それぞれの垂直円弧の端が「過去」を介して接続されていることを示しています。最初のケースは図への移行を示しています。 3残りの2つのケースはやや複雑ですが、水平アークのさまざまな組み合わせを追加することで新しいセクションを取得できることを明確に示しています。

ただし、水平アークのすべての組み合わせが新しいセクションにつながるわけではありません。一部の組み合わせは、図5に示す3つの理由で受け入れられない場合があります。

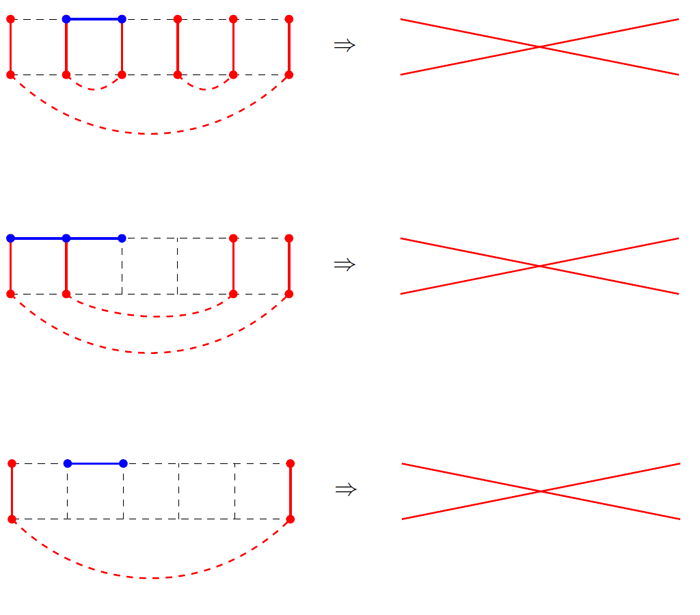図5-無効な遷移の例 3つの可能なケース

最初のケースでは、3つのチェーンの1つが前もって閉じているため、ハミルトニアンサイクルは判明しません。 2番目のケースでは、3つの円弧が1つの頂点に収束します。最後に、3番目のケースは、一部の頂点がアイドル状態であることが判明したため不可能です（そして、ハミルトニアンサイクルはすべての頂点を通過する必要があります）。

したがって、格子のすべての可能なセクションと、水平アークを含めることで取得可能なセクションに関する情報があるとします。この情報はすべて、有限状態マシンの形式で表すことができ、そのノードはカットされ、アークは遷移の可能性を示します。図図6に、3×n格子用に構築されたこのような有限状態マシンの例を示します。

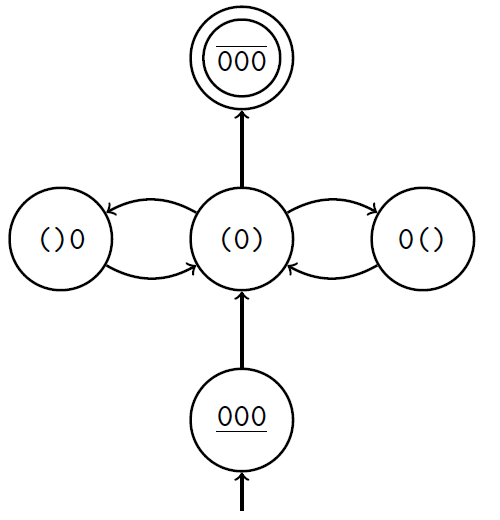図6-3×n格子の状態マシン

ラティスP ₃ ×P _nにいくつのサイクルがあるかという質問に対する答えは、オートマトンの初期状態から最終段階にnステップで進む方法の数です。どうやってやるの？私は2つの方法を知っています：悪いと良い。悪いところから始めましょう。

4.伝達マトリックス法

この問題を解決する1つの方法は、伝達マトリックス法と呼ばれます。可能なすべてのカットに1からNまでの番号を付けますが、初期状態は1、最終状態はNです。番号T _ijがセクションiから番号jのセクションを取得する方法の数に等しい行列Tを作成します。。格子P _m ×P _nの問題の解は、数（T ⁿ ） _{1、Nです。}
たとえば、格子P ₃ ×P _{nの場合、}オートマトンが既に構築されているので（図6）、伝達行列を書き出すことができます。

図7-伝達行列、または有限状態マシンの隣接行列図 6とその6度

図図７は、格子Ｐ _３ ×Ｐ _ｎ上のハミルトニアンサイクルの輸送行列Ｔを示す。問題の解決策は数（T ⁿ ） ₁₅です。たとえば、（T ⁶ ） ₁₅ = 4は、格子P ₃ ×P ₆上のハミルトニアンサイクルの数です。

ただし、実際には、この問題を解決する方法は、格子上のハミルトニアンサイクルの転送行列のサイズが3774×3774（説明セクションの表1を参照）であり、パーソナルコンピューターのRAMに収まる場合、最大でm = 12に適用されます。たとえば、格子P ₁₂ ×P ₂₀の答えには33桁が含まれ、格子P ₁₂ ×P _100の場合、桁数は174に達するため、長い数値は行列自体に格納されます。

「モジュラー演算」セクションでは、計算の速度を犠牲にして長い数値を取り除く方法を示しますが、それでも転送行列の巨大な成長からは救いません。したがって、問題を解決するこの方法を悪いと呼びました。

5.マトリックスを使用しないソリューション

この解決方法は、奇妙ではないので、伝達行列法とも呼ばれますが、行列は明示的に表示されません。したがって、ロシア語の文献では、このような方法を動的計画法（有限状態機械を使用）と呼ぶのが慣例です。

このメソッドの意味は、ステートマシンの各頂点に到達する方法の数をkステップで保存することです。ステップk = 0では、この数値は開始頂点を除くすべての頂点で0です。ステップk = 0で開始頂点に到達する方法の数は、定義により1と見なされます。ステップkの頂点iにPメソッドがあり、ステップk + 1に進んで、すべての頂点のメソッドの数に番号Pを追加しますiから到達できるj ただし、このためには、iから取得できる頂点を知る必要があります。つまり、再び行列を保存します。実際には、それは必要ではありません。頂点iに到達し、それが指定するセクションを把握し、そこから出てくる可能性のあるすべてのセクションを再構築します。

これがプログラムでどのように実装されるかは、個々の問題です。私のアプローチを説明します。キューQがあり、そこにセクションが（ブラケットシーケンスの形式で）格納され、そこに含まれる方法の数があるとします。アルゴリズムの開始時に、ゼロと1に等しいメソッドの数で構成されるセクションがキューに格納され、キューと一緒にセクションとそれらに到達する方法の数も格納するハッシュテーブルがあります。アルゴリズムの開始時には、テーブルは空です。

ステップkで、キューから次のセクションiを取得し、Pがそこにあるウェイの数を取得します。 iから取得したすべての可能なカットのセットJを作成します。 Jの各jについて、ハッシュテーブルにあるかどうかを確認します。そうでない場合は、メソッドPの数とともにjをテーブルに追加します。はいの場合、jに入力できるメソッドQの数をテーブルから取得し、代わりに番号P + Qを書き込みます。例外は、jがゼロカットに等しい場合です。これは、最終状態にあり、数値Pを回答に追加する必要があることを意味しますが、ハッシュにゼロカットを追加しないでください。

ステップkの最後では、キューは空なので、データをハッシュテーブルからキューに移動し、ハッシュをクリアして、ステップk + 1に進みます。

私は、オープンアドレッシングとダブルハッシュのハッシュを使用しています。コリジョンの数は、呼び出しごとに0.6です。つまり、60％のケースで、表に従って1つのステップが実行され、他のケースではすぐに実行されます。これは、このようなタスクに適したハッシュであると思います。

6.アルゴリズムの複雑さ

最初に、複雑さの上限を指摘し、次に実際に実際に判明することを示します。

ゼロによって放出され、長さmのすべての通常のブラケットシーケンスのセットは、コンテキストフリーの文法によって生成されたアルファベット{ 0 、（、） }上の長さmのMotskinワードです

Z→Y | Y （ Z ） Z、
Y→ε| 0 Y、

ここで、εは空の単語です。このような単語の数は、組み合わせの考慮事項から計算できます。

この式で、kは括弧のペアの数です。合計記号の下の最初の式（小数部と最初の2項係数）は、正しいブラケットシーケンスの数を示すカタロニア語番号であり、2番目の2項係数は、m個の位置に2k個のブラケットを置く方法の数です（残りの位置をゼロで埋めます）。

したがって、格子上のハミルトニアンサイクルのすべての可能なカットの数は、少なくともMotskinワードの数を超えず、Motskinワードはほぼ3 ^mの速度で成長します。実際、一部は受け入れられない可能性があるため、このようなセクションははるかに少なくなっています。たとえば、 （0）000または（（）0）0などのカットは、幅6のラティスでは受け入れられません。これは、ハミルトニアンサイクルを構築するときに取得できないためです。ディスカッションセクションでは、表が表示されます。 1は、いくつかのmのカットの総数を示します。実際には、Motzkinの単語の3分の1だけが許可されており、対称性を考慮すると、5分の1だけを保存すれば十分であることがわかります。

説明します。一部のセクションはパリンドロームであり、対称反射下で一致していますが、互いに対称なセクションは1つのセクションとして保存できます。たとえば、カット（（））（）および（）（（））は同じと見なすことができます。これを念頭に置いて、平均でMotzkinの単語の5分の1だけがプログラムに保存されるべきであることがわかります。

セクションごとに、2 ^m-1の方法で水平方向の円弧を設定する必要があります。そして、これらすべてを合わせてn回行う必要があります。

合計、アルゴリズムの複雑さはO（6 ^m・m ^-1/2・n）です。しかし、実際には、多くのセクションが受け入れられないという事実により、実際にはアルゴリズムの複雑さはO（5 ^m・n）になります。これは、アルゴリズムの観察中に発生しました。

使用されるメモリに関しては、リソースの主要部分はキューとハッシュテーブルによって占有されます。 m≤32の各セクションは、ブラケットと数値0を格納するために2ビットが必要であるため、64ビット整数に格納できます。さらに、すべてのリソースを永久に消費する長い演算。しかし、長い演算を放棄して、計算を遅くすることができる1つのトリックがあります。

7.モジュラー演算

さまざまな素数を法として答えを計算してみましょう：2 ³¹ -1 = 2147483647、2147483629、2147483587、...これを行うには、選択したさまざまなモジュールの数だけプログラムを実行する必要があります（もちろん、2〜3個のモジュールを一度に読み込むことができます。メモリ内）。中国の剰余定理によれば、答えは使用されたすべての素数の積まで復元することができます。すべての素数の積が問題の答えより大きい場合、答えは一意に復元されます。適切な数のモジュールを選択する方法は？

たとえば、2つのモジュールについて、サイズ16 x nの格子上のサイクル数をカウントしてみましょう。 n = 1,2、...、16.とするそれから答えを得る

[0、1、128、405688、24980352、776813457、729683652、1087605227、2000673777、456710131、1550214608、568568229、2047094091、1175631455、380271385、1536681549]（mod 2147483647）。

[0、1、128、405688、24980352、776813727、729709644、1107434405、301217473、1373982040、103268356、218837622、1185113726、2085126539、1315887233、2008046410]（mod 2147483629）。

中国の剰余定理によると、次のとおりです。

[0、1、128、405688、24980352、32989068162、3101696069920、2365714170297014、309656520296472068、2415277789552788286、3926649012293853406、726889843182193849、153366515247378747、1645735649663585962、3698490188721496226、1337259901989820598（MOD・2147483647 2147483629）。

2つのモジュールがあるかどうかを確認する方法は？この問題では、数値が指数関数的に増加することは明らかであるため、対数は線形に増加する必要があります。対数を取る（例：自然）：

[-INF、0、4.852、12.91、17.03、24.22、28.76、35.40、40.27、42.33、42.81、41.13、39.57、41.94、42.75、41.74]。

2つのモジュールの積の対数は42.98です。数の差はほぼ同じ量で単調に増加し、n = 9から始まるため、何らかの理由で増加が停止することがわかります。さらに、この場所では限界に達し、それを超えると数を超えることはできません。つまり、2つのモジュールでは不十分でした。 4つのモジュールを取り、答えを復元しましょう。

[0、1、128、405688、24980352、32989068162、3101696069920、2365714170297014、309656520296472068、168435972906750526954、27738606105535271640888、12142048779807437697982030、2344813362310160031818110686、888511465584607682074513271223、191678405883294971709423926242394、65882516522625836326159786165530572]（MOD 2147483647 2147483629···2147483587 2147483579）。

対数は等しい：

[-IFN。、0、4.852、12.91、17.03、24.22、28.76、35.40、40.27、46.57、51.68、57.76、63.02、68.96、74.33、80.17]。

数値は厳密に増加し、ほぼ同じ量だけ増加します。選択した4つのモジュールの積の対数は85.95であり、シーケンスの最後の数値よりも著しく大きくなっています。これは、答えが正しいことを意味します。これを確認するには、Googleにリクエスト「65882516522625836326159786165530572」を入力します。

8.議論と結果

このアルゴリズムを使用して、22×100ラティスのサイクル数を計算できました。 1つのモジュールの計算は、クラスターの32コアで約30時間続きました。合計で、約50のモジュールが必要でした。コアごとに必要なメモリは1 GB未満です。コンピューティングの過程で、ソリューションの定量的特性に関する情報を収集しました。表の中。以下の1はこの情報です。

m	実際のカット数	モッツキンの単語数
3	3	4
4	6	9
5	12	21
6	23	51
7	62	127
8	109	323
9	365	835
10	607	2188
11	2355	5798
12	3774	15511
13	16020	41835
14	25188	113634
15	113198	310572
16	176061	853467
17	821923	2356779
18	1270562	6536382
19	6097041	18199284
10	9387784	50852019
21	46013564	142547559
22	70652188	400763223

表1-Motskin番号とメモリに保存するために必要な実際のカット数の比較

最初の列では、格子幅m。 3番目-長さmのモツキン語の数。中央の列は、有効なカットの実際の数を示します（対称性が考慮され、最終状態は計算されません）。

正方格子P _2n ×P _2nのハミルトニアンサイクルの数を確認する場合、このシーケンスへのリンクがソースのリストにあります。