小さな紹介
画像のマッチングの問題が一般的に解決される場合から始めましょう。 以下をリストできます：パノラマの作成、ステレオペアの作成、2次元投影からのオブジェクトの3次元モデルの再構築、原則として、オブジェクトの認識とデータベースからのモデルの検索、複数の写真でのオブジェクトの動きの追跡、アフィン画像変換の再構築。 おそらく、このリストにあるアプリケーションを見逃したか、まだこのアプリケーションを思いついていないかもしれませんが、おそらく、記述子のアプリケーションがどのようなタスクを解決するつもりなのか、すでにお分かりでしょう。 そのようなタスク（コンピュータービジョン）を検討している知識の分野は非常に若く、すべての結果をもたらすことに注意する必要があります。 上記の問題をすべて完全に解決する明確な普遍的な方法はありません。 すべての入力画像用。 しかし、すべてがそれほど悪いわけではありません。さまざまな種類のより狭いタスクを解決する方法があることを知っておく必要があり、問題を解決する方法を選択する際の多くは、タスク自体の種類、オブジェクトの種類、それらが描かれているシーンの性質、個人的な好み。
また、読む前に、
SURFメソッドについての記事を斜めに見るのは間違いではありません。
一般的な考え
人は画像を比較して、視覚的に直感的なレベルでオブジェクトを選択できます。 ただし、マシンの場合、画像はデータセットのことを言っているだけではありません。 一般的に言えば、この人間のスキルを機械に「与える」ための2つのアプローチを説明できます。
一般的な画像に関する知識の比較に基づいて、画像を比較する特定の方法があります。 一般的な場合、これは次のとおりです。各画像ポイントについて、特定の関数の値がこれらの値に基づいて計算され、特定の特性を画像に割り当てることができます。その後、画像を比較するタスクはそのような特性を比較するタスクに削減されます 概して、これらの方法は単純であるだけでなく、実際には理想的な状況でしか受け入れられません。 これには多くの理由があります：画像内の新しいオブジェクトの外観、他のオブジェクトとの重なり、ノイズ、ズーム、画像内のオブジェクトの位置、3次元空間内のカメラの位置、照明、アフィン変換など。 実際、これらの方法の質の低さは、その主なアイデア、つまり 画像の
各点が特性に寄与しているという事実により、この寄与がどれほど悪くてもよい。
最後のフレーズは、そのような問題を回避するという考えにすぐにつながります：何らかの形で特性に寄与するポイントを選択するか、さらに良いことに、特別な（キー）ポイントを選択して比較する必要があります。 これについて、キーポイントで画像を比較するというアイデアを思いつきました。 画像を何らかのモデル、つまりキーポイントのセットに置き換えていると言えます。 すぐに、同じオブジェクトの別の画像上で見つかる可能性が最も高い、描かれたオブジェクトのポイントを特別と呼びます。 検出器は、画像からキーポイントを抽出する方法です。 検出器は、画像変換に関して同じ特異点を見つけることの不変性を保証する必要があります。
不明な点は、ある画像のどのキーポイントが別の画像のキーポイントに対応するかを判断する方法だけです。 結局のところ、検出器を使用した後は、特異点の座標しか決定できず、それらは各画像で異なります。 これが記述子の出番です。 記述子は、他の特別なポイントと区別するキーポイントの識別子です。 次に、記述子は、画像変換に関して特異点間の対応を見つける不変性を保証する必要があります。
その結果、画像マッチングの問題を解決するための次のスキームが得られます。
1.キーポイントとその記述子が画像上で強調表示されます。
2.記述子の一致により、互いに対応するキーポイントが強調表示されます。
3.一致するキーポイントのセットに基づいて、画像を変換するためのモデルが構築され、これを使用して1つの画像から別の画像を取得できます。
各段階には、問題とそれらを解決するためのさまざまな方法があり、元の問題の解決に一定の意性をもたらします。 次に、ソリューションの最初の部分、つまり、SIFT（スケール不変特徴変換）メソッドを使用した特異点とその記述子の割り当てについて検討します。 基本的に、SIFTメソッドのアルゴリズムについて説明しますが、このアルゴリズムが機能する理由ではなく、そのように見えます。
最後に、不変性を取得したいいくつかの変換をリストします。
1）バイアス
2）回転
3）スケール（1つの同じオブジェクトが異なる画像上で異なるサイズになることがあります）
4）明るさの変化
5）カメラ位置の変更
最後の3つの変換に関する不変性を完全に取得することはできませんが、少なくとも部分的にそうすることは悪くありません。
特別なポイントを見つける
特異点の検出における主なポイントは、ガウスのピラミッド（ガウス）とガウスの差（ガウスの差、DoG）のピラミッドの構築です。 ガウス（またはガウスフィルターによってぼやけた画像）は画像
ここで、Lは座標（x、y）を持つ点でのガウス値であり、sigmaはぼかし半径です。 Gはガウスコア、Iは元の画像の値、*は畳み込み演算です。ガウス分布の差は、レンズの半径が異なるガウス分布から元の画像の1つのガウス分布をピクセルごとに減算することによって得られる画像です。
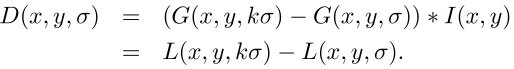
簡単に言えば、スケーラブルなスペースについて話しましょう。 スケーラブルな画像空間は、元の画像のさまざまなバージョンのセットであり、フィルターによって平滑化されています。 ガウスのスケーラブル空間は線形であり、シフト、回転、およびスケールに関して不変であり、局所的な極値をシフトせず、半群の性質を持っていることが証明されています。 ガウスフィルターによる画像の異なる程度のぼかしを、特定のスケールで撮影された元の画像として撮影できることが重要です。
一般に、スケール不変性は、異なるスケールで撮影された元の画像のキーポイントを見つけることで実現されます。 これを行うために、ガウスピラミッドが構築されます。スケーラブル空間全体がいくつかのセクション（オクターブ）に分割され、次のオクターブが占めるスケーラブル空間の一部は、前のものが占める部分の2倍です。 さらに、あるオクターブから別のオクターブに移動すると、画像のリサンプリングが行われ、サイズが半分になります。 当然、各オクターブは無限の数のガウス画像にまたがるため、ぼかし半径に沿った特定のステップで、特定の数Nの画像のみが構築されます。 同じステップで、オクターブを超える2つの追加ガウス分布が完成します（合計N + 2が得られます）。 さらに、なぜこれが必要なのかがわかります。 次のオクターブの最初の画像のスケールは、番号Nの前のオクターブからの画像のスケールに等しくなります。
ガウスのピラミッドの構築と並行して、ガウスのピラミッド内の隣接する画像の違いから構成されるガウスの違いのピラミッドが構築されます。 したがって、このピラミッド内の画像の数はN + 1になります。
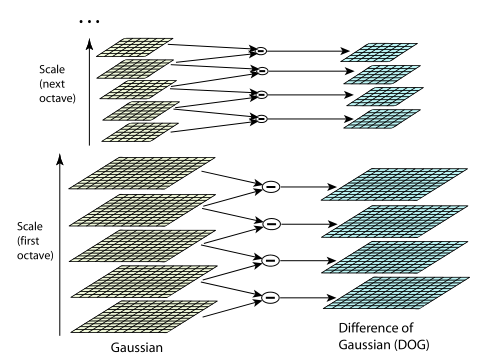左側の図はガウスのピラミッドを示し、右側はその違いを示しています。 各差分は2つの隣接するガウス分布から取得され、差分の数はガウス分布の数より1少ないことを概略的に示しています。次のオクターブに移動すると、画像サイズは半分になります。ピラミッドを構築した後、問題は小さいままです。 ガウス分布の差の極値である場合、特異点を考慮します。 極値を検索するには、図に概略的に示す方法を使用します
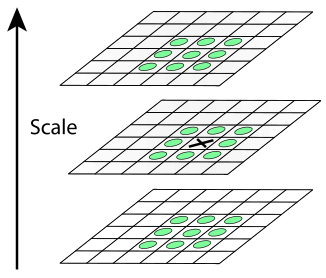十字でマークされたポイントのガウス分布の差の値が、丸い円でマークされたポイントのすべての値よりも大きい（小さい）場合、このポイントは極値ポイントと見なされますDoGピラミッドの各画像で、極値点が検索されます。 現在のDoGイメージの各ポイントは、その8つの近隣およびDoG内の9つの近隣と比較されます。これらは、ピラミッド内で1レベル上下します。 このポイントがすべての隣接ポイントよりも大きい（小さい）場合、ローカル極値のポイントと見なされます。
なぜオクターブで「余分な」画像が必要なのかが明らかになったと思います。 DoGピラミッドの画像の極値点を確認するには、N + 1'eが必要です。 また、DoGピラミッドでN + 1'eを取得するには、ガウスのピラミッドにN + 1'eおよびN + 2'eの画像が必要です。 同じロジックに従って、DoGピラミッドに0番目のイメージ（1番目をチェックするため）を構築し、ガウスピラミッドにさらに2つのイメージを構築する必要があると言えます。 しかし、現在のオクターブの最初の画像のスケールは前の画像のN'eと同じであることを思い出して（これは既にチェックされているはずです）、少しリラックスして読み進めてください:)
特異点の指定
奇妙なことに、前の段落では、キーポイントの検索は終了していません。 次のステップは、重要な役割に対する極値点の適合性に関するいくつかのチェックです。
まず、特異点の座標はサブピクセル精度で決定されます。 これは、計算された極値のポイントで取得された2次テイラー多項式でDoG関数を近似することで実現されます。
ここで、DはDoG関数、X =（x、y、sigma）は分解点に対する変位ベクトル、最初のDoG導関数は勾配、2番目のDoG導関数はヘッセ行列です。テイラー多項式の極値は、導関数を計算し、それをゼロに等しくすることにより求められます。 結果として、計算された極値の点の変位を、比較的正確に取得します
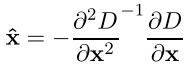
すべての導関数は、有限差分式によって計算されます。 その結果、ベクトルX ^のコンポーネントに関連して、次元3x3のSLAEを取得します。
ベクトルX ^のコンポーネントの1つが0.5 * grid_step_in this_directionよりも大きい場合、これは実際には極値ポイントが誤って計算されたため、指定されたコンポーネントの方向に隣接ポイントに移動する必要があることを意味します。 隣接するポイントについては、すべてが再び繰り返されます。 この方法でオクターブを超えた場合、この点を考慮から除外する必要があります。
極値点の位置が計算されると、この点でのDoG値は、式によって小ささについてチェックされます
このテストが失敗した場合、そのポイントは低コントラストのポイントとして除外されます。
最後に、最後のチェック。 特定のポイントがオブジェクトの境界上にあるか、照明が不十分な場合、そのようなポイントは考慮から除外できます。 これらのポイントは、境界に沿って大きなベンド（2次導関数のコンポーネントの1つ）を持ち、垂直方向に小さくなります。 この大きな曲がりはヘッセ行列Hによって決定されます。サイズ2x2のHはテストに適しています。
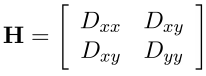
Tr（H）を行列のトレース、Det（H）を行列式とします。
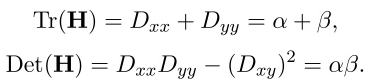
大きいベンドと小さいベンドの比率をrとし、
それから
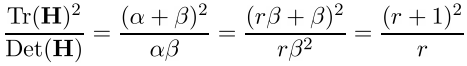
そして、ポイントはさらに考慮されます
キューポイントの向きを見つける
ある点がキーであることを確認したら、その方向を計算する必要があります。 後で見るように、ポイントにはいくつかの方向があります。
キーポイントの方向は、特異点に隣接するポイントの勾配の方向に基づいて計算されます。 勾配のすべての計算は、キーポイントのスケールに最も近いスケールで、ガウスのピラミッドの画像で実行されます。 参考：点（x、y）での勾配の大きさと方向は、式によって計算されます
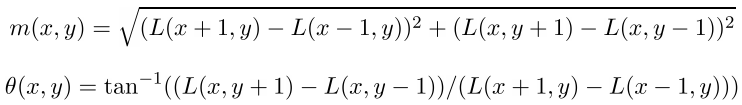mは勾配の大きさ、シータはその方向最初に、勾配が考慮されるキーポイントのウィンドウ（近傍）を定義します。 本質的に、これはガウスコアとの畳み込みに必要なウィンドウになり、丸くなり、このコアのぼかし半径（シグマ）は1.5 * key_point_scaleです。 ガウスカーネルの場合、いわゆる「3シグマ」ルールが適用されます。 それは、ガウス核の値が3 *シグマを超える距離でゼロに非常に近いという事実にあります。 したがって、ウィンドウの半径は[3 * sigma]として定義されます。
O方向のヒストグラムからキーポイントの方向を見つけます。ヒストグラムは360度のギャップを均一にカバーする36個のコンポーネントで構成され、次のように形成されます：ウィンドウ（x、y）の各ポイントは、m * G（x、y、sigma ）、勾配方向theta（x、y）を含むギャップをカバーするヒストグラムのコンポーネントに。
キーポイントの方向は、最大ヒストグラム成分でカバーされるギャップにあります。 最大成分（max）と2つの隣接成分の値は放物線によって補間され、この放物線の最大点がキーポイントの方向として使用されます。 ヒストグラムに少なくとも0.8 * maxの値を持つコンポーネントがさらにある場合、それらは同様に補間され、追加の方向がキーポイントに割り当てられます。
記述子の構築
次に、記述子に直接進みましょう。 前の定義では、記述子が何をすべきかを述べていますが、それが何であるかではありません。 原則として、記述子は（その機能を処理する限り）任意のオブジェクトにできますが、通常、記述子はキーポイントの近傍に関する情報です。 この選択はいくつかの理由で行われました：歪み効果は小さな領域に小さな影響を及ぼしますが、一部の変更（画像内のオブジェクトの位置の変更、シーンの変更、オブジェクト間のオーバーラップ、回転）は記述子にまったく影響しません。
SIFTメソッドでは、記述子はベクトルです。 キューポイントの方向と同様に、ハンドルは、キューポイントに最も近いスケールで、特定のキューポイントウィンドウの勾配に基づいて計算されます。 記述子を計算する前に、このウィンドウはキーポイントの方向の角度だけ回転され、それによって回転に関する不変性が達成されます。 まず、図を見てみましょう
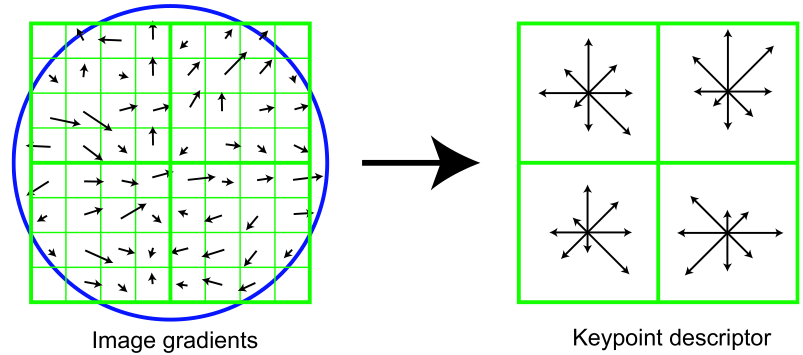
ここでは、画像の一部（左）と（右）が模式的に示されています。 まず、左を見てみましょう。 ここでは、小さな正方形で示されたピクセルを見ることができます。 これらのピクセルは、記述子の正方形ウィンドウから取得され、さらに4つの等しい部分に分割されます（以下、これらを領域と呼びます）。 各ピクセルの中央にある小さな矢印は、そのピクセルのグラデーションを示します。 興味深いことに、このウィンドウの中心はピクセルの間にあります。 キーポイントの正確な座標にできるだけ近いものを選択する必要があります。 最後に表示される詳細は、ガウスコアを持つ畳み込みウィンドウを示す円です（キーポイントの方向を計算するためのウィンドウに似ています）。 このカーネルでは、シグマはハンドルウィンドウの幅の半分に等しいと定義されています。 将来、記述子のウィンドウ内の各ポイントの値は、重み係数として、このポイントでのガウスコアの値で乗算されます。
それでは、右側を見てみましょう。 ここでは、次元2x2x8の特異点の概略的に描かれた記述子を見ることができます。 ディメンション値の最初の2桁は、水平方向および垂直方向の領域の数です。 右側の画像の左側にあるピクセルの特定の領域をカバーする正方形は、これらの領域のピクセルに基づいて作成されたヒストグラムをカバーします。 したがって、記述子の次元の3桁目は、これらの領域のヒストグラムの成分の数を意味します。 領域内のヒストグラムは、3つの小さい方向のヒストグラムと同じ方法で計算されますが、
1.各ヒストグラムは360度プロットもカバーしますが、8つの部分に分割します
2.記述子全体に共通のガウスカーネルの値は、重み係数と見なされます（これについては既に説明しました）。
3.トリリニア補間係数は、もう1つの重み係数として取得されます。
3つの実座標（x、y、n）を記述子ウィンドウの各勾配に割り当てることができます。xは勾配への水平距離、yは垂直距離、nはヒストグラムの勾配方向への距離です（記述子の対応するヒストグラムを意味します）この勾配が寄与します）。 基準点は、ハンドルウィンドウの左下隅とヒストグラムの初期値です。 単一のセグメントの場合、領域の水平および垂直サイズをそれぞれxおよびyに、ヒストグラムコンポーネントの度数をnに使用します。 トライリニア補間係数は、勾配の各座標（x、y、n）に対して1-dとして決定されます。dは、勾配の座標からこの座標が入る単位区間の中央までの距離です。 ヒストグラム内の勾配の各発生には、3つの線形補間の3つの重み係数すべてが乗算されます。
キューポイント記述子は、受信したすべてのヒストグラムで構成されます。 既に述べたように、図32の記述子の次元はコンポーネント（2x2x8）ですが、実際には、次元128の記述子が使用されます（4x4x8）。
結果の記述子は正規化され、その後、値が0.2より大きいすべてのコンポーネントが値0.2にトリミングされ、その後記述子が再び正規化されます。 そのため、記述子はすぐに使用できます。
最後の言葉と文学
SIFT記述子には欠陥がないわけではありません。 すべての受信ポイントとその記述子が要件を満たすわけではありません。 当然、これは画像マッチングの問題のさらなる解決に影響します。 場合によっては、解決策が存在しても、見つからない場合があります。 たとえば、レンガの壁の2つの画像からアフィン変換（または基本行列）を検索する場合、壁は異なるキーポイントの記述子を互いに類似させる繰り返しオブジェクト（レンガ）で構成されているため、解決策が見つからない場合があります。 このような状況にもかかわらず、これらの記述子は多くの実際に重要なケースでうまく機能します。
さらに、この方法は特許を取得しています。
この記事では、SIFTアルゴリズムのスキームの例を説明します。 このアルゴリズムが何であり、なぜ機能するのか、記事「天井から」で取り上げたいくつかのパラメーターの値を選択する理由（たとえば、記述子の正規化の数値0.2）に興味がある場合は、ソースを参照する必要があります
David G. Lowe「スケール不変のキーポイントからの独特の画像特徴」前の記事の主な内容を繰り返す別の記事。 いくつかのポイントを詳しく説明します
Yu Meng「スケール不変特徴変換（SIFT）メソッドの実装」