はじめに
おそらく、何世紀にもわたって、生命の起源と理由についての質問として、科学者にとって何の関心もありませんでした。 自然はどのように人間の脳を作成すると推測しましたか？ 私たちの頭の中のニューラルネットワークの構造を決定するものと、単一細胞からの多細胞生物の自動アセンブリはどのように機能しますか？ なぜ特定の段階でヒト胚の開発は、あなたは魚のエラのようなものを観察することができますか？
そして、単純な好奇心盛な素人でさえ、有機化学の詳細に悩まされず、そのような質問は無視されません。
ここで気取らない成長している生物を収集するために使用することができるおもちゃのデザイナー、だろう。 次に、生活の現象の多くを示す非常に単純化されたモデルを構築すると、生活の構造の質問への答えに近づくことができ、少なくともこれらの答えを見つける場所を理解することができます。
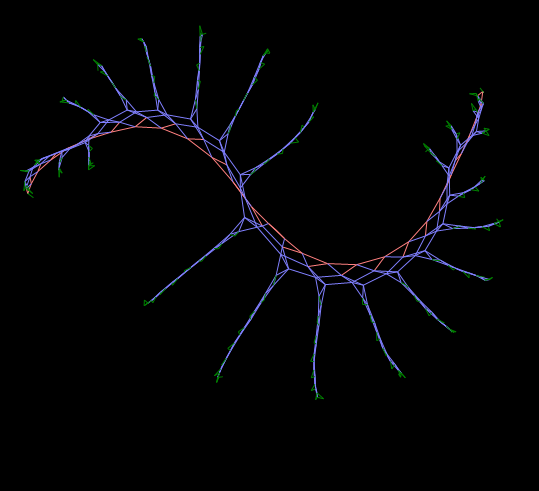
このような非常に単純化されたモデルは、「ライブグラフ」になることがあります。グラフ上の有限オートマトンは、各ノードに有限数の状態とノード間の新規接続の作成または変更を制御する一連の特定の実行デバイス（オートマトン）が含まれます。
「キャベツの育て方を見てください！」 （C）皇帝とダウンシフターディオクレティアヌス
この記事では、「リビンググラフ」の化身の1つ-グラフ展開GUCA（Graph Unfolding Cellular Automata）のセルオートマトンについて説明します。 GUAのデモンストレーションは、
Silverlightプラグインを接続したブラウザーで直接「感じる」ことができます。 Webアプリケーションは、成長グラフの最初のインスタンスのいくつかの短い寿命を視覚化します-遺伝的アルゴリズムの「遺伝子工学」と「自然に選択された」形式の両方の自己工学製品。
初期グラフが1つのノードのみで構成され、グラフの生成されたすべてのノードがルールセットの同じコピーを持ち、ルールの新しい反復がトリガーされるたびに、さまざまな構造の発達を観察することができます。 最初のノードは多細胞生物の胚に似ており、グラフの残りのノードは細胞に似ており、ルールセットは染色体に、ルール自体は遺伝子に似ていることが簡単にわかります。
起源
そしてそれはすべて 、GUCAのアイデアが生まれた研究で、
人工ニューラルネットワーク （ANN）に
魅了されて始まりました 。
少し思い出させてください。 人工制御システムに広く応用されている人工ニューラルネットワークは、相互に接続された「ニューロン」であると考えることができます。 しかし、いくつかのルールに従って単一のネットワークに接続された「ニューロン」は、その構成要素の機能を大幅に超えるシステムを形成します-同じ加算器。 システムは、全体として、パターン認識、分類、信号フィルタリングの機能にすでにアクセスしています。これらはすべて、複雑な「インテリジェントな」制御システムを構築するために必要です。
ニューラルネットワークの使用の夜明けに、研究者によってネットワークトポロジが設定され、接続パラメーターは、解決される問題に関する累積データを使用する所定のアルゴリズムに従って選択されました。 十分に単純なタイプのニューロンに対して、ネットワークトポロジを構築するタスクが十分に決定的で解決可能な場合（ドメイン自体の問題の解決可能性を意味しない）、フィードバック付きのニューラル非線形動的ネットワークのカスケードを使用する場合、このタスクは簡単ではなく、構築を委任するというアイデアが生まれましたネットワークニューラルネットワークトポロジ。 自然界で見つかった方法自体が助けになりました。
私たちは、遺伝的アルゴリズムを使用してニューラルネットワークのトポロジを構築する神経
進化的手法について話している。
神経進化の方法
このような方法のレビューは最近habrで公開されました：[1]
habrahabr.ru/blogs/artificial_intelligence/84015 、
そのようなアルゴリズムを実装するための既知の方法については語りません。ネットワーク/グラフの間接コーディングの基本的な規定のみを思い出します。これは、検討中のGUCA法の基礎にもなります。その実装は、局所性、使用されるルールの文脈上の選択、および「プログラムされた死」によってのみ区別されます。
ニューラルネットワークをコード化する間接的な方法では、ネットワークインスタンスの「ゲノム」で、トポロジはノードとリンクの明示的なリストではなく、その小さな断片からネットワークを構築するルールによって間接的に定義されます。 結局のところ、この方法では、小さな胚から動物、そして人間の脳を開発しています。
また、遺伝的アルゴリズムは、コードのランダム生成または変更、「ゲノム」のデコードの「結果」の評価（つまり、フィットネス関数を使用した結果のニューラルネットワークの評価）、および最適な代表の選択を提供します。
オブジェクト制御システム（ロボット、マニピュレーター）の役割を果たすニューラルシステムの場合、フィットネス関数は、特定の環境（迷路、オブジェクトの処理中、飛行中、戦闘中など）における制御オブジェクトの操作可能性です。
さらに、間接的なコーディング方法には次のプロパティがあります。
1）モジュール方式。 単純な規則に従ったフラクタル構造の再帰的構築と、いくつかの標準ブロック、身体構造の要素の繰り返し。
2）完全性。 任意のネットワーク（グラフ）に対して、コードを選択できます。
3）冗長性。 コードには、デコード結果に影響しない冗長データが含まれる場合があります。
4）（コンテキストコーディング規則の使用の対象）
a。 ニューラルネットワークを通過する信号に応じたトポロジ生成
b。 再生-局所的な損傷を伴う回復可能性
レビュー[1]から、研究者の主な努力は、ニューロン/ネットワークの原理を設計し、そのパラメーターをコーディングするのではなく、ネットワークトポロジをコーディングする方法を多少成功させることを目的としていることがわかります。ニューラルネットワーク。」
トポロジー培養
確かに、同じ遺伝的アルゴリズムと間接コーディング（実際には、有向グラフ、およびNSからのさらに抽象化-無向グラフ）を使用してネットワークトポロジを「成長」させる問題を特定することは有益です。 適応度関数（インスタンスの生存の成功を決定する）は、管理対象オブジェクトに対処するニューラルネットワークの機能ではなく、たとえば、トポロジの幾何学的プロパティです。 グラフは、平面又は空間内に展開すると - フィットネス評価グラフには、得られる画像の特性であってもよいです ラスタ。
（ニューラルネットワークから抽象化する建物のトポロジは、）
できるようになります 狭い問題に焦点を当て ：•
ANN以外の領域 （メカニズムの自動アセンブリ、コンピューターネットワークまたはウイルスでの分散コンピューティングの構成、戦闘ロボットの相互作用）でより広範な
アプリケーションを見つけ
ます 。
•研究者に
結果 （最終だけでなく中間も）を
視覚的に提示します。これは、因果関係をよりよく理解するためのアルゴリズムの開発に役立ちます。 さらに、視覚的な表現は、アイデア/解決策/行き止まりを提案できます。
•
コーディングトポロジのさまざまなソリューションを
比較したり
、コーディングトポロジの成功したソリューションをさまざまなデザインの「ニューロン」と組み合わせたりすることがより客観的です。 客観的に-すなわち 特定の適用分野に関係なく。
•
フィットネス関数を
計算するの が簡単 （高速で安価）
です （制御システムとしてのニューラルネットワークの適合性の評価と比較して）-つまり、 派生問題に計算リソースを含む追加のリソースを費やすことなく、正確にトポロジカルアルゴリズムを研究する。
同時に、上記の「モジュール化」、「再生」の好奇心の性質など - は、研究のために利用可能のままになります。
動物の脳の進化は、多細胞生物の形状の進化によって達成された結果からも発生することを付け加えることができます（軸対称-軟骨-脊椎-脊髄-非対称性-脳の脳圧縮）。
そのような方法の一つは、グチャグラフセルラオートマトン、作業は次のセクションで提示されるの原理の展開です。
GUCAグラフ展開セルラーオートマトン
GUCAの「リビンググラフ」は、各ノードがいずれかの状態（状態の数は有限）にある有限
セルオートマトンであり、ノード自体の状態とその環境の両方に応じて、特定のルールに従って別の状態に移行できます。 これらのルールはすべてのノードで同じであり、時間的に一定であり、すべてのノードで同時に同期して実行されます。
セルオートマトンの古典的な代表は
ライフゲームです。 Living Graphsと古典的なゲームLifeとそのバリエーションの主な違いは、細胞内オートマトンが長方形の平面上に配置されておらず、可変数の接続された近傍を持つグラフのノードに配置されていることです。
同時に、レビュー[1]で説明されているネットワークトポロジのコーディング方法のほとんどとは異なり、「ライブカウント」GUCAは次の原則を公言しています。
•適用可能なルールのコンテキスト選択
•ローカルおよびワンステップの変更のみ
•誕生だけでなく死
奇妙なことに、これらの機能はすべて、最初は「Life」セルラーマシンに固有でしたが、問題を解決する一連のルールと操作の長期にわたる検索の結果として選択されました。
グラフの展開は最もシンプルで完全です。
ただし、講義の演習の1つで除去操作が提案されました[2]。
原則
したがって、GUCAの「ライブグラフ」では、ノードはいずれかの
状態にあります。 また、特定
の操作
条件下で 、グラフに対して
操作を実行する
ルールがあります。
「リビンググラフ」のいくつかのインスタンスについて、上記の「メタルール」を満たす一連のルールの例は次のとおりです。
1.「ノードが状態Aにある場合、状態Bにリンクされたノードを作成します」
2.「ノードが状態Bにあり、リンクの数が2未満の場合、接続されたノードを状態Bに作成します」
3.「ノードが状態Bにあり、前の状態がBだった場合、状態Cに進みます」
4. ...
状態は、有限集合の要素の1つです。 A、B、C、D、...のアルファベットの数字または文字で表すことができます。
操作 グラフに対してさまざまな操作を実行できることは明らかです。ノードの追加/分離、ノードの接続グループへの置換、ノードの結合。 私は、任意の複雑な構造を再現するのに十分であると思われる4つの基本的な操作に決めました。
•ノードの状態Xへの遷移（したがって、状態Xは操作のオペランドです）
•現在のノードに関連付けられた新しいノードの誕生。 新しいノードXのステータス
•ノードを状態Xの最も近い未接続ノードに接続する
•状態Xのノードの切断
次に、ルール内の操作を規定する条件について説明します。 ノードの現在の状態と、このノードと他のノード間の接続数に依存することに限定されませんでした。 これらの条件に、ノードの以前の状態への依存と、ノードの親/分割の数への依存を追加しました（結局、各ノードは、操作のリストに従って、1つの親ノードによってのみ生成されます）。
条件：•ノードは状態Xにあります
•ノードの以前の状態はYです
•ノード接続の数-C1からC2
•ノードの祖先の数（ノードの生成元）-P1からP2。
最後の条件とノード分割の数のカウンター（
テロメラーゼの類似体）は、生物全体および/またはその個々のモジュールの開発を停止するために導入されています。
私はまた、「死のホスト」「Xの状態にあるすべてのノードに接続ノード」操作と見なさ - しかし、彼らは冗長と見なさ。 「部門カウンターのリセット」操作を導入することも考えています。 すべての操作はローカルであり、ノードを中心に「回転する」（ノードまたは唯一の彼の即時の環境を変更する）ことに注意してください。
ただし、おそらく読者はより一貫性のあるルールのシステムを見つけることができます。
文法規則
GUCAルールは、現在の状態を文字で示し、前の状態を括弧で囲んだ文字、「c」（接続から）の隣人の数、「p」（親から）の親の数を示す短い形式で記述することもできます。 以前の状態は条件に無視されている場合は、括弧でダッシュを示します。 操作ルールを条件から条件とコロン記号で区切り、次のように可能な操作を示します。
•別の状態Xへの遷移の操作はXで示されます。
•接続されたノードを作成する操作を示します++ ++ X
•ノードXに接続する操作は+ Xで示されます。
•ノードXから切断する操作は–Xで示されます。
次に、「生活グラフ」一連のルールのいくつかのコピーのために文法の助けを借りて書かされます。
1. A（A）、p = 0：++ B
2. B（-）、c <2：++ B
3. B（B）：C
4. A（A）：G
5. C（B）、c = 1：G
6. G（G）、c <5：H
グラフの開始ノードが状態「A」にある場合、ルールの適用を12回連続して繰り返した後、「フィンガーダンベル」を取得します。
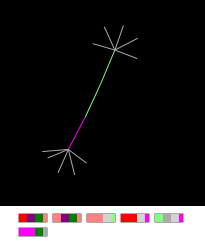図は、その遺伝子マップをマッピング「Paltsastayaのgantelki」と条件をカウントします。これは、数年前にグラフでステートマシンをデバッグするために設計した最初のグラフです。 それは非常にシンプルで理解しやすいので、先駆者に敬意を表すためだけに言及しています。 彼の「ゲノム」に規定されているルールは単純です。初期状態Aのノードから、（ストリングが状態Gの）ノードで終わる短い文字列が生まれます。このルールは機能します。近隣の数が5以下の場合、新しい近隣を作成します。
以下、グラフがプレーン上および遺伝子マップの条件付きマップ上に表示される場合、赤は状態A、ピンク-B、緑-C、ラズベリー-Gを示します。
「paltsastoy gantelki」の遺伝子№5をオフにすると、「フリーク」を作成することができます - 「普通の手を」：
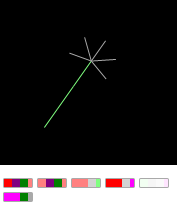
遺伝子を再びオンにすると、2番目の「アーム」が元に戻ります。
したがって、一連の単純なルールでグラフのトポロジを決定できます。 一般的に、グラフトポロジは、一連のルールとそのノードの初期状態だけでなく、いくつかのグローバルな制限（たとえば、最大反復数またはノード接続の最大可能数）によっても決定されます。
アイデアを確認する
上記のルールシステムがトポロジのグラフを構築するのに十分であることを確認する1つの方法は、構築の「制御問題」を解決することです。 特定の人物について考えて、それが生まれる「遺伝子」を考えてみてください。 そして、構想された図が何らかの方法で構築できない場合、ルールのシステムはグラフの成長だけでなく、複雑な人工ニューラルネットワークの構築にも適しているとは考えられません。
「制御タスク」は一方では非常にシンプルで、他方では「指標」である必要があり（「スペクタキュラー」と混同しないでください）、複雑な生物の定性的特性と効果（モジュール性、ハイブリダイゼーション、自己回復... このような例には、図の内部で成長する単純なフラクタル、多数のセルを含むグリッド、および単純に「野生」の植物が含まれます。
これらのタスクの一部は、念頭に置いて、または紙で解決するのが非常に難しく（長く）、信頼性がありませんでした（答えはしばしば同意しませんでした）。これらの最初の実験を実施するために、「実験的なセットアップ」を用意しなければなりませんでした。
パイロットインストール（Silverlightアプリケーション）
この実験では、「遺伝コード」と再生マシンをデバッグすることを可能にするソフトウェアアプリケーションでした。 さらに、次のことができます：
•グラフの成長プロセスを視覚化します。
•グラフの成長中に染色体と遺伝子の活動の色の「マップ」を視覚的に表示する
•特定の遺伝子をオフにしたり、「生きているグラフ」をカットした結果がどうなるかを確認します。
「実験セットアップ」のSilverlightデモバージョンは、
http：//roma.goodok.ru/guca/GUCA_DemoSL.htmlで入手できます
。
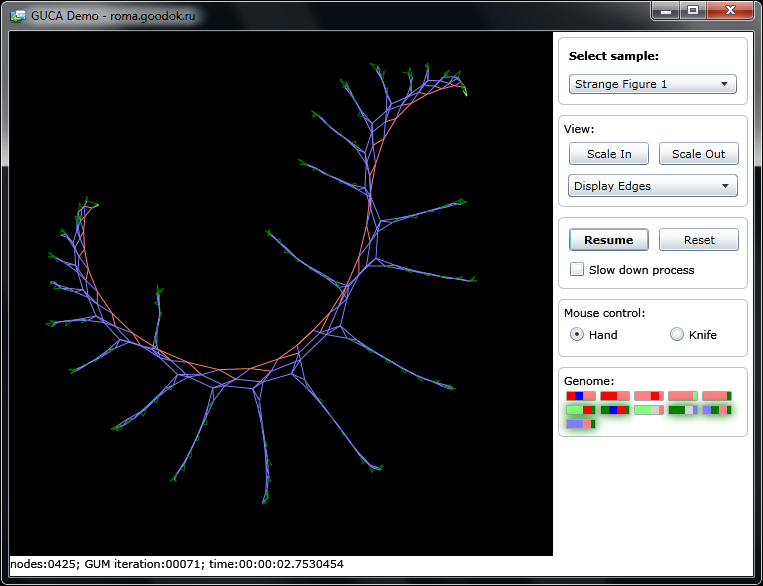グラフを成長させるための「実験セットアップ」の図Silverlightバージョンでは、グラフの開発プロセス、染色体マップ上の遺伝子の活性、個々の枝をナイフで「切断」することができます。グラフの展開を
開始するには、右側の「コントロールパネル」のドロップダウンリストから例（サンプルの選択）を選択し、開始ボタン（「開始」）をクリックする必要があります。
背景が黒い中央の領域には、単一の胚ノードからの成長の過程でグラフが表示されます。 ノードのさまざまな状態が対応する色で表示されます。 表示のスケールと外観を変更したり、グラフの成長を遅くしてプロセスの詳細を検討したりできます。
グラフの発達と寿命を観察できるだけでなく、「メス」（「ナイフ」スイッチ）で切り込むか、特定の遺伝子をオフにして「フリーク」を生み、「致命的な結果」または「癌性腫脹」を達成することで、このプロセスに
介入できます
染色体の
「マップ」 （「ゲノム」）は右下に条件付きで
表示されます。その上の各長方形は「遺伝子」（ルール条項）に対応します。 繰り返しますが、ルールの条件にあるノードの状態、ルール自体、およびルールのオペランドにあるノードの状態は色分けされています。 成長グラフの緑色のプロセスのルールの次の反復の実行中にアクティブであったこれらの遺伝子をマーク照射。
マウスを個々の「遺伝子」の長方形に向けると、遺伝子によってエンコードされたルールのデコードがテキスト形式で表示され、マウスボタンをクリックして、選択した遺伝子をオフ（またはオン）にできます。
この記事では、「実験装置」デバイスの説明については触れませんが、「アセンブリ」自体は非常に興味深い職業でした-グラフ理論と離散数学に加えて、数理物理学、幾何学などの方程式を数値的に解く知識と経験さらに、その遺伝的な「ソース」コード自体は進化の結果であり、遠い先祖の遺産を含んでいます-結局、Delphi 7.0で最初のバージョンと設計の決定が実装されました。 WPF |«！Hellow世界»あなたも、これはSilverlightのプラットフォームでは、私の最初のものであると言えるでしょう。 QuickGraph（グラフとアルゴリズム）およびAForge（遺伝的アルゴリズム）ライブラリの使用にのみ注意します。
最も簡単な例
それでは、ライブプロパティを示す「生きているグラフ」のいくつかの簡単な例を見てみましょう。 いくつかのインスタンス（たとえば、前述の「指で描かれたダンベル」）は、生きているグラフの世界（つまりMe）の神の原理によってのみ構築されたもの、他は進化の結果、さらには遺伝子組み換え製品です。
「毛の輪」
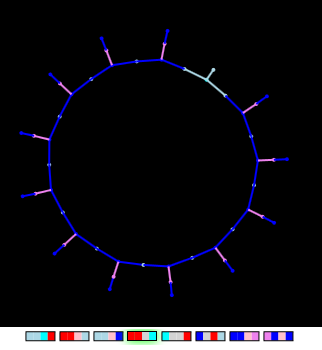
この図は、遺伝子組み換え製品です！ まず、遺伝的アルゴリズムの助けを借りて、内側から無限に成長する円が得られました（この場合の適合度関数は、グラフのトポロジ特性（2つの面の必須の存在のみ）に依存していました）。 次に、別の「遺伝子」が追加されました-「髪の遺伝子」（遺伝子マップの右端）
内側から成長する「生物」を開始すると、新しいエッジの挿入の周期的な繰り返しの結果、円の個々のセグメントがどのように見えるかを観察できます。
指周囲（ハイブリッド）
「フィンガーダンベル」と「ヘアリーサークル」の遺伝子を取り、それらを「胚」の1つの染色体に結合すると、ダンベルの「フィンガーネス」の特性と「ラウンド」特性の両方を継承するハイブリッドがそこから出現します。
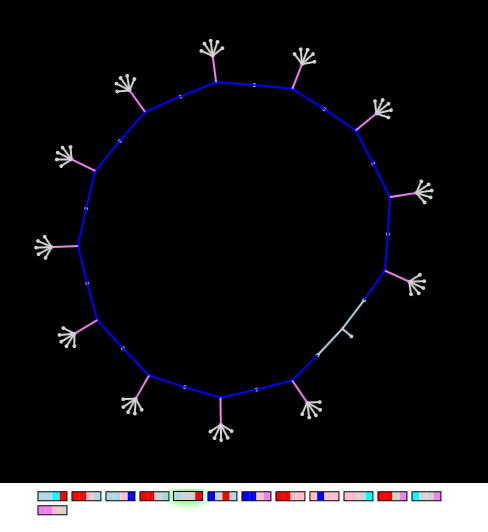図ハイブリッド「指の形のダンベル」と「毛むくじゃらの円周」には共通の特性があります「指の形をしたダンベル」の遺伝子の一部は、グラフ展開のプロセス全体で非アクティブのままであることに注意してください（遺伝子マップでは遺伝子の活動が緑色で強調表示されます）。
「ブッシュ」（フラクタル）
2「遺伝子」の最も単純な遺伝コードは、任意の大きなサイズのグラフを作成します。」 枝を切り取ると、「ブッシュ」は以前のサイズと形状でほぼ瞬時に回復します。
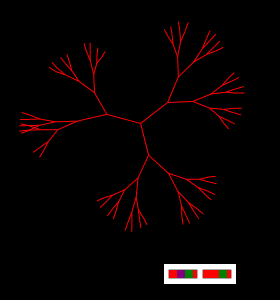原始フラクタルは、遺伝子のペアによってのみ定義されます。ココシュニク（長方形メッシュ）
これと次の2つの奇妙な形は、正方形の形で正方形のグリッドを作成しようとした結果です。
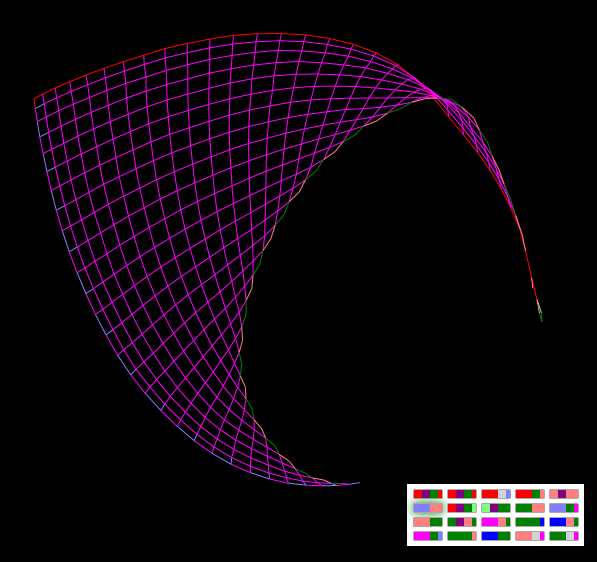ココシュニクの描画-長方形グリッドの拡大遺伝子のペアを変更することにより、任意の大きさの（および小さい）グリッドを拡大できます。 ナイフで穴を開けることができます。 遺伝子13「O（O）：+ L」をオフにして、展開後にオンにしてみてください。
奇妙な図1と奇妙な図2
「奇妙な図1」は私の間違いです。 実際、目標は正三角形のグリッドを作成することでした。 この図は、記事の最初の図に示されています（図1）。 生きているグラフ上でプロセスを直接カットし、カットオフする代わりに新しいプロセスをリリースした場合、図はより全体的な外観になります。
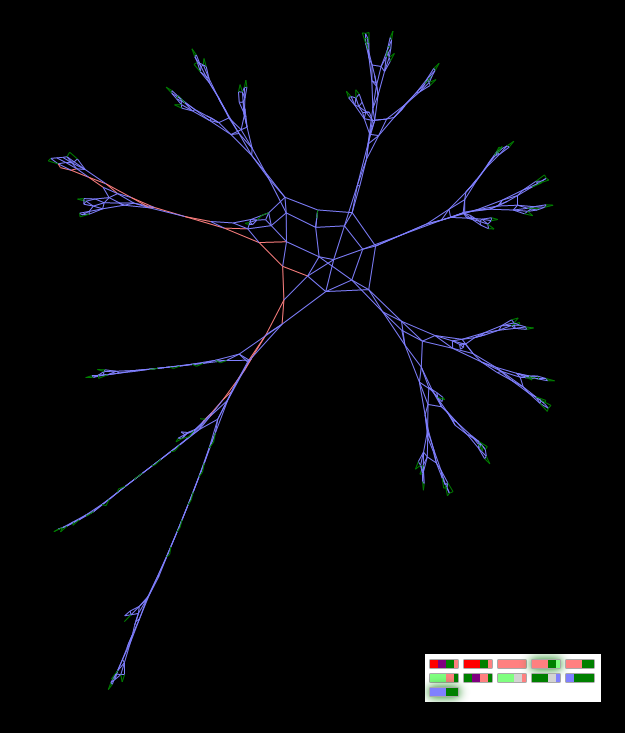切り抜き後の図「奇妙な図」奇妙な図2 。 この図の染色体は、「奇妙な図2」の染色体とは遺伝子が1つだけ、または遺伝子の一部（近縁）でさえ異なりますが、「解読」の結果の形式は前のインスタンスの形状に似ていません。
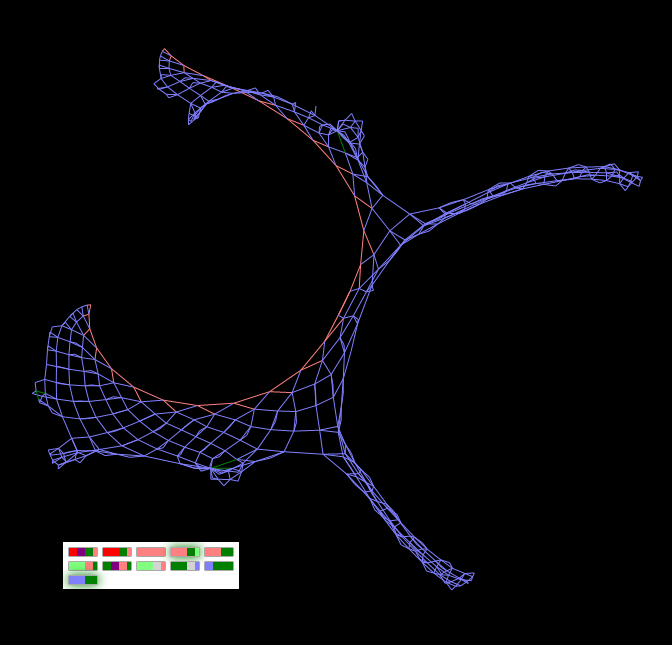「ストレンジ図2」 - 「国の数字1」の近親は、 -単一の遺伝子だけで異なります「プロセスのある六角形」（進化の結果）
この図の10個の遺伝子を取得するには、遺伝的アルゴリズムの何千もの反復が必要でした。 ロシア語に翻訳されたフィットネス関数は次のようなものでした：「顔の数が2に近く、ノードの数が1から6、ノードの数が3から6、遺伝子の数が0であるほど、グラフが生き残る可能性が高くなります」（ノードの次数-数接続）
この種の進化は、いくつかの飛躍を遂げました。三角形、突起のある正方形、不規則な突起のある6つの正方形、そして最後に正しいものです。 展開のプロセスを遅くすると、図を作成するためにどのソリューションの進化が見つかったかを確認できます。
「葉」のある六角形-遺伝的アルゴリズムの結果おわりに
したがって、有限状態マシンやグラフなどの抽象的なオブジェクトを使用して、多面的な生き物のように見えるシステムを面白い方法で作成できることがわかりました。これは、「生きているグラフ」の基礎と生物の幾何学的形状の法則の原則の一般性を示しています。
しかし、これは私たちが生命の秘密を明らかにしたという意味ではありません。 「生きグラフ」の進化の法則を探求する：これは単にあなたが上に移動できることを意味します。 私は、サンプルアプリケーションでは、私たちは「個体発生」と進化の結果ではなく、進化そのものを観察したことを思い出してください。
後続の研究の問題は、「生きたグラフ」モデルの境界を決定する方法、および過度の詳細（形態の複雑さに対する遺伝子長の依存性、進化ツリー内の種の位置に関する遺伝情報の統計、許容されるセットの進化速度）によって負担されない進化モデルの定量的および定性的規則性を検索することです操作など）。
最も効果的な進化アルゴリズムを決定したこれらの研究の結果に基づいて、初期の分野で「生きているグラフ」を適用しようとすることができます：人工ニューラルネットワークまたはロボット、「動物」、および人工制御システムの進化の研究。 , «» . - « ».
, , .
-, , . , « » . , « ».
文学
[1] « »
http://habrahabr.ru/blogs/artificial_intelligence/84015/[2] «Evolutionary Computation for Modeling and Optimization» Daniel Ashlock, January 12, 2004
http://orion.math.iastate.edu/danwell/ma378/UPDATE «» xml. :
« 1» . , … , .
UPDATE 2 (1.8) .