いくつかの可能な投資に1億ドルを投資するとします。 これらの各投資には、異なる価値と異なる期待収益があります。 最大の利益を得るには、どのようにお金を使うかを決めなければなりません。
このタイプのタスクは、ポートフォリオ構築タスクと呼ばれます。 固定サイズのポートフォリオ(1億ドル)に収まるいくつかのポジション(投資)があります。 各ポジションには独自の収益性があります。 ポートフォリオに配置され、最大の利益をもたらすポジションのセットを見つける必要があります。
多くの人は、ここではヒューリスティックは不要であり、徹底的な検索で十分に対応できると言うでしょう。 ブランチとボーダーの方法があるため、完全な検索は必要ないと言う人もいます。 しかし、可能な投資の数が65である場合はどうでしょうか。 完全な決定ツリーには、7 * 10 ^ 19を超えるノードが含まれます。 分岐バインドメソッドがこれらのノードの10分の1を反復し、コンピューターが毎秒100万ノードをチェックするとします。 これらの条件下では、問題を解決するのに200万年以上かかります。 ヒューリスティックが使用されるのは、このような複雑なタスクのためです。 興味があれば、猫を歓迎します。
丘を登る
丘を登るヒューリスティックな方法は、現在のソリューションに変更を加えて、可能な限りターゲットに近づけます。 このプロセスは、夜に山の頂上に到達しようとする迷子のように見えるため、ヒルクライミングと呼ばれます。 遠くにあるものを見るには暗すぎる場合でも、彼は常に山の頂上に到達しようとすることができます。
もちろん、旅行者が小さな丘の頂上で止まり、ピークに達しない可能性があります。 この問題は、このヒューリスティック手法を使用する場合に発生します。 アルゴリズムは、ローカルに最適なソリューションを見つけることができますが、最良のソリューションではありません。
投資ポートフォリオを形成するタスクの目標は、許容限度以下の合計値を持つポジションのセットを選択することであり、合計利益は可能な限り大きくする必要があります。 このタスクのヒルクライミングヒューリスティックは、すべてのステップで最大の利益をもたらすポジションを選択します。 同時に、この決定は利益を最大化するという目標をよりよく達成します。
アルゴリズムは、最初に最大利益のあるポジションをソリューションに追加し、次に最大利益のある次のポジションを追加します(価格全体が許容範囲内にある場合)。 最大の利益でポジションに参加することは、価値の限界がなくなるまで続きます。
以下の投資のリストでは、プログラムは最大の利益(900万ドル)を持つため、最初に取引Aを選択します。 次に、トランザクションCが選択されるのは、最大の利益が残っているためです(800万ドル)。 この時点で、許容される1億個のうち、9,300万個がすでに使用されており、アルゴリズムはトランザクションを選択できなくなります。 このヒューリスティックを使用して計算されたソリューションには、要素AおよびCが含まれ、費用は9,300万で、1,700万の利益があります。

クライミングヒューリスティックは非常に迅速にポートフォリオを満たします。 要素が最初に利益の降順で並べられている場合、アルゴリズムの複雑さは約O(N)です。 プログラムは、資金の制限がなくなるまで、単にリスト内を移動し、最大の利益を持つポジションを追加します。 リストがソートされていない場合、このアルゴリズムの複雑さはN * log(N)です。 これは、ツリーのすべてのノードを完全に列挙するために必要なO(2 ^ N)ステップよりもはるかに優れています。 20ポジションの場合、このヒューリスティックは約400ステップ、ブランチとボーダーの方法-数千、徹底的な検索-200万以上を使用します。
最小コスト法
この戦略は、ある意味では山登り法の反対であり、最小コスト法と呼ばれています。 ソリューションを各ステップで可能な限り目標に近づける代わりに、ソリューションのコストを削減することができます。 各ステップで投資ポートフォリオを形成する例では、最小コストのポジションがソリューションに追加されます。
この戦略は、ソリューション内にできるだけ多くのポジションを配置します。 これは、すべてのポジションの値がほぼ同じ場合にうまく機能します。 しかし、高価な取引が大きな利益をもたらす場合、この戦略はチャンスを逃す可能性があり、可能な限り最高の結果をもたらしません。
上記の投資の場合、最小コスト戦略は、まずソリューションに2,300万のトランザクションEを追加してから、2700万のポジションDと3000万のCを選択することから始まります。百万ドルであり、もはや単一の投資を行うことはできません。
結果のソリューションのコストは8000万で、1800万の利益が得られます。これは、丘を登るヒューリスティックが提供するソリューションよりも数百万優れていますが、最小コストのアルゴリズムは、丘を登るアルゴリズムよりも常に効率的に機能するとは限りません。 どの方法が最適なソリューションを提供するかは、特定のデータによって異なります。
最小コストのヒューリスティックと丘を登るヒューリスティックを実装するプログラムの構造はほとんど同じです。 唯一の違いは、既存のソリューションに追加される次の位置の選択です。 利益が最大のポジションの代わりに最小コストの方法が、最低コストのポジションを選択します。 2つの方法は非常に似ているため、複雑さは同じです。 位置が適切にソートされている場合、両方のアルゴリズムはO(N)の次数の複雑さを持ちます。 ランダムな位置の配置では、それらの複雑さはO(N * log(N))のオーダーになります。
バランスの取れた利益
ヒルクライミング戦略では、追加されたポジションの価値は考慮されません。 彼女は、たとえ大きな価値があるとしても、最大の利益を持つポジションを選択します。 最小コスト戦略では、ポジションによってもたらされる利益は考慮されません。 彼女は、たとえ利益がほとんどなくても、低コストでアイテムを選択します。
バランスの取れた利益ヒューリスティックは、利益とポジション値の両方を比較して、選択する必要があるポジションを決定します。 各ステップで、ヒューリスティックは利益対価値の比率が最も高い要素を選択します(投資がポートフォリオに含まれた後、合計価格が許容範囲内に留まる場合)。
テーブルに新しい列-利益/価値の比率を含めます。 このアプローチでは、最も高い比率が0.27であるため、位置Cが最初に選択されます。 次に、Dを0.26の比率で、Bを0.20の比率で追加します。 この時点で、1億人のうち9,200万人が費やされ、1つのポジションをソリューションに追加することはできません。
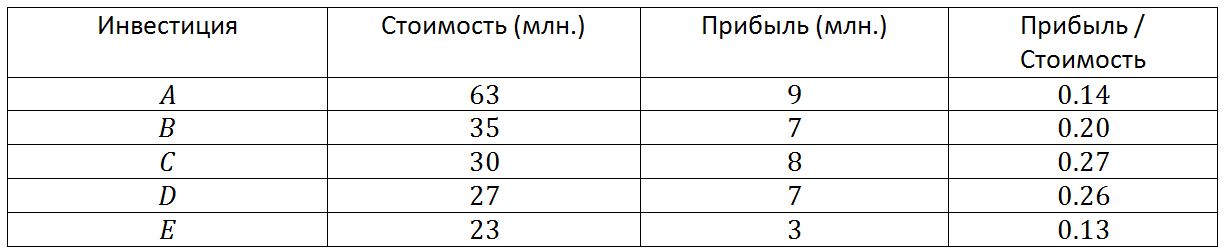
このソリューションの価値は9,200万で、2,200万の利益をもたらします。これは、最小コストの方法を使用して見つかったソリューションよりも400万、ヒューリスティックな山登りで見つかったソリューションよりも500万優れています。 さらに、見つかった解決策は一般的に可能な限り最良のものであり、徹底的な検索による検索または分岐と境界の方法によって確認されます。 しかし、バランスの取れた利益はまだ発見的であるということを理解することが重要です。したがって、この助けを借りても、最良の解決策が常に見つかるとは限りません。 多くの場合、この方法は、丘を登る方法で見つかったソリューションよりも優れたソリューションを最小限のコストで見つけますが、これは常に発生するとは限りません。 バランスの取れた利益のヒューリスティックを実装するプログラムの構造は、山登りプログラムの構造と最小コストとほぼ同じです。 唯一の違いは、ソリューションに追加される次の位置を選択する方法です。 このヒューリスティックの複雑さはO(N)に比例し、予備ソートの対象となります。 位置が任意に配置されている場合、アルゴリズムの複雑さはO(N * log(N))になります。
ランダム法
ランダム検索
ランダム検索は、その名前に従って実行されます。 各ステップで、アルゴリズムはコストの境界を満たすランダムに選択された位置を追加します。 このタイプの列挙は、モンテカルロ法と呼ばれます。
ランダムに選択されたソリューションが最良である可能性は低いため、許容可能な結果を得るには、検索を数回繰り返す必要があります。 一見、良い解を見つける可能性は非常に小さいように見えますが、この方法を使用すると驚くほど良い結果が得られることがあります。 初期データとチェックされたランダム解の数に応じて、このヒューリスティックは、多くの場合、山登り法と最小コストよりもうまく機能します。
ランダム検索の利点は、この方法の理解と実装が簡単であることです。 特定のタスクで丘を登る方法、最小コスト、または利益を減らす方法を実装する方法を想像するのは難しいこともありますが、ソリューションをランダムに生成することは常に簡単です。 非常に複雑な問題を解決する場合でも、ランダム検索が最も簡単な方法です。
シーケンシャルアプローチ
別の戦略は、ランダムなソリューションから始めて、一貫した近似を行うことです。 ランダムに生成されたソリューションから始めて、プログラムはランダムな選択を行います。 新しいソリューションが以前のソリューションの改善である場合、プログラムは変更を統合し、他のアイテムのチェックを続けます。 変更によってソリューションが改善されない場合、プログラムはそれを拒否し、新しい試みを行います。
投資ポートフォリオを形成するタスクの一貫した近似の方法を実装することは特に簡単です。 プログラムは、試行ソリューションからランダムな位置を選択し、現在の位置から削除するだけです。 次に、資金の限度がなくなるまで、決定にランダムにポジションを追加します。 削除されたポジションのコストが非常に高い場合、プログラムはその場所ではなく、いくつかのポジションを追加できます。
ランダム検索と同様に、このヒューリスティックは理解と実装が簡単です。 複雑な問題を解決するために、丘を登るアルゴリズム、最小コスト、利益の減少を作成するのは簡単ではありませんが、逐次近似のための発見的アルゴリズムを書くのは非常に簡単です。
停止の瞬間
ランダムな変更を停止するタイミングを決定するには、いくつかの良い方法があります。 たとえば、一定数の変更が許可されます。 N要素のタスクの場合、NまたはN ^ 2のランダムな変更を加えてから、プログラムを停止できます。
別の戦略は、連続的な変更が改善をもたらすまで変更を加えることです。 いくつかの連続した変更で改善が見られなくなったらすぐに、プログラムを停止できます。
局所最適
プログラムが試用ソリューションでランダムに選択された位置を置き換える場合、改善できないソリューションが見つかる可能性がありますが、それでも最良のソリューションではありません。 例として、次の一連の可能な投資を検討してください。

アルゴリズムが初期解として位置AとBをランダムに選択するとします。 その価値は9,000万に等しく、1,700万の利益をもたらします。
プログラムがAまたはBのいずれかを削除すると、ソリューションのコストがかなり高くなるため、プログラムは新しいポジションを1つだけ追加できます。 ポジションAとBの利益が最大であるため、それらを別のポジションに置き換えると、総利益が減少します。 このソリューションから誤って1つのポジションを削除しても、改善にはつながりません。
最適なソリューションにはポジションC、D、Eが含まれます。総コストは98百万、総利益は1,800万です。このソリューションを見つけるには、アルゴリズムはポジションAとBの両方を一度にソリューションから削除し、代わりに新しいポジションを追加する必要があります。
そのような決定は、小さな変更でソリューションを改善できない場合、ローカル最適と呼ばれます。 プログラムがローカル最適で停止しないが、グローバル最適を探す2つの方法があります。
まず、プログラムを変更して、ソリューションからいくつかの項目を削除することができます。 プログラムがランダムに選択した2つのアイテムを削除する場合、この例に適したソリューションを見つけることができます。 ただし、大規模なタスクの場合、通常、2つのポジションを削除するだけでは十分ではありません。 プログラムは、3、4、またはそれ以上のポジションを削除する必要があります。
より簡単な方法は、異なる初期ソリューションでより多くのテストを実行することです。 最初の解決策の一部は局所的な最適化につながる可能性がありますが、そのうちの1つはグローバルな最適化を実現します。
焼鈍方法
アニーリング法は熱力学から借用されています。 アニーリング中、金属は高温に加熱されます。 溶metal中の分子は急速に振動します。 金属がゆっくりと冷却されると、分子が整列し始め、結晶が形成されます。 この場合、分子は徐々にエネルギーが最小の状態に変わります。
金属が冷えると、隣接する結晶が互いに結合します。 ある結晶の分子は、最小限のエネルギーで一時的にその位置を離れ、別の結晶の分子と結合します。 結果として生じる大きな結晶のエネルギーは、2つの元の結晶のエネルギーの合計よりも小さくなります。 金属が十分にゆっくりと冷却されると、結晶は単純に巨大になります。 分子の最終的な配列の総エネルギーは非常に低いため、金属は非常に強くなります。
高エネルギー状態から始まり、分子は最終的に低エネルギー状態に達します。 最終的な位置に向かう途中で、彼らは多くの地元のエネルギー最小値を通過します。 各水晶の組み合わせは、局所的な最小値を表します。 結晶は、より小さな結晶の構造の時間分解能によってのみ最小エネルギー状態にすることができ、それにより、システムのエネルギーが増加し、その結果、結晶が結合できます。
アニーリング方法は、問題の最良の解決策を見つけるために同様の方法を使用します。 プログラムがソリューションを検索するとき、ローカルの最適状態にとどまることがあります。 これを避けるため、次のオプションで結果がすぐに改善されない場合でも、彼女は時々ソリューションをランダムに変更します。 これにより、プログラムはローカル最適を終了し、最適なソリューションを見つけることができます。
プログラムがこれらの変更に焦点を合わせるのを防ぐために、しばらくするとアルゴリズムはランダムな変更を行う確率を変更します。 1つの変更を行う確率はP = 1 / e ^(E /(k * T))です。ここで、Eはシステムに追加される「エネルギー」の量、kは問題の種類に応じて選択される定数、Tは「温度」に対応する変数「。
まず、Tの値は非常に高くなければならないため、変更の可能性も非常に高くなります。 しばらくすると、Tの値が減少し、ランダムな変化の確率も減少します。 変更が解決策を改善できないポイントにプロセスが到達し、Tの値が非常に小さくなり、ランダムな変更が非常にまれになると、アルゴリズムはジョブを終了します。
投資のポートフォリオを形成するタスクの場合、Eは、変更の結果として利益が減少する値です。 たとえば、利益が1,000万ドルのポジションを削除し、利益が700万ドルのポジションに置き換えると、システムに追加されるエネルギーは3になります。Eの値が大きい場合、変化の確率は小さいため、大きな変化の確率以下。
ヒューリスティック手法の比較
異なるヒューリスティック手法は、異なるタスクで異なる動作をします。 投資のポートフォリオを形成する問題を解決するには、その単純さを考えれば、バランスの取れた利益の発見的手法で十分です。 シーケンシャルアプローチ戦略も非常に効果的ですが、より多くの時間が必要です。 他のタスクについては、この章で検討されていないものを含め、他のヒューリスティックが最適な場合があります。
ヒューリスティックは、ブルートフォースおよびブランチおよびバインドメソッドよりもはるかに高速に動作します。 いくつかのヒューリスティックアプローチ(丘を登る、最小コスト、バランスの取れた利益など)は、考えられる解決策を1つしか考慮しないため、非常に高速に動作します。 これらのメソッドは非常に高速に動作するため、すべてを順番に実行し、得られた3つのソリューションから最適なものを選択することが理にかなっている場合があります。 もちろん、このソリューションが最高であることを保証することは不可能ですが、確かに十分です。