TAUダーウィニズム

まえがき

「サイバーヤードおじさんフェディヤの強さはまさに3匹です」とポールは述べ、サイバーヤードの腸から調整ブロックを取り除きました。 「私はすでにここでフェディアを知っています。」 楽しい、そばかす。 非常に無菌状態の若い男。 これはあなたの親notではありませんか？

アルカディとボリス・ストルガツキー（正午。XXII世紀）。

この記事は、動的システムの識別の問題に対する遺伝的アルゴリズムの適用可能性に専念しています。
更新： TAU Darwinism Continuation発行：Ruby実装

はじめに

物理システムの分析の一部としての数学モデルの構造の識別とは、オブジェクトの物理モデルを記述する代数表現（方程式）を見つけることを意味します。多くのシステム識別方法はパラメトリックです。識別可能なオブジェクトのモデルの構造が決定され、指定された式を使用して、このモデルのパラメーターが計算されます。この記事では、遺伝的プログラミングを使用してオブジェクトの最適な数学モデルを選択する方法を説明します。
この点でのGAの利点は、これらのアルゴリズムが、ヘルプを使用して識別できるシステムのリストを制限せず、入出力システムを表すデータのセットに適用できることです。 GAを使用する場合、識別されたオブジェクトの構造を事前に決定する必要はありません。最適なモデル構造は、ランダムに生成された個人（モデル）の集団の進化中に見つかります。

用語

母集団 -個人の有限集合。
個々 -生物、1つまたは複数の染色体で表されるデータ構造。各染色体は、解決される問題のパラメーターの多次元空間のポイントです。
染色体 -遺伝子の順序付けられたセット。
遺伝子 -染色体内の位置によって特徴付けられ、いくつかのプロパティ（パラメーター）の値が含まれています。
遺伝子型 -染色体全体の遺伝子のマップ。
表現型 -特定の遺伝子型の遺伝子の可能な組み合わせのセット、すなわちタスクパラメータの空間における点群。
対立遺伝子 -各遺伝子の可能な値のセット、すなわち特定のプロパティの値のセット。
遺伝子座は、染色体内の遺伝子の位置です。

識別オブジェクト

不均一な微分方程式は、識別可能なオブジェクトの最初の数学的モデルと見なされます。簡単にするために、2次微分方程式を例として使用します。

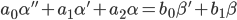（1）

式（1）で、「 '」（アポストロフィ）は時間微分-演算子d / dtを意味します。 αは出力座標（例えば、平衡位置からの敏感な要素の偏差）です。 β-入力アクション、制御（たとえば、 SEに作用し、その偏差につながる力）。
演算子形式（s = d / dt）では、この方程式は次のようになります。

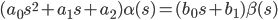（2）

式（2）に従って、伝達関数がコンパイルされます-入力と出力の比率：

（3）

（3）では、分母はシステムの「特性方程式」です。ダイナミクスの主な特性（安定性など）を決定します。この方程式の根は、動的システムの極と呼ばれます。分子の根は、動的システムのゼロと呼ばれます。
伝達関数（3）は、分子と分母が2項と3項の積である分数の形式で書き換えることができます。

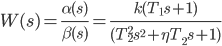（4）

この場合、分子と分母の両方にそれぞれ1つの多項式が含まれますが、一般的な場合、次数4以上の方程式にはそれらのいくつかがあります。さらに、それぞれが複素平面上の点に対応します。実軸上の点は二項に対応し、実軸上にない点は三項に対応します。最後のステートメントは、3項に2つの複素共役根しかない場合にのみ真です。それ以外の場合、この三項式は2つの二項の積として表すことができます。
式（4）で、係数「T」は時定数であり、係数ηは減衰減少量です（振動または減衰係数の指標でもあります）。

遺伝暗号

（2）の形式で識別可能なオブジェクトの数学モデルを記述するには、実数を使用した遺伝子コーディングスキームを使用すると便利です。この場合、各遺伝子の対立遺伝子の数は、アルゴリズムのソフトウェア実装の実数の長さ（バイナリ表現のビット数）によって決まります。
フォーム（2）の数学モデルに2つの染色体をエンコードさせます。1つは入力用（右側）、もう1つは出力用（左側）です。染色体内の遺伝子は、方程式（2）のいずれかの用語に対応しています。遺伝子の値は、方程式の変数の係数の値に等しくなります。さらに、染色体内の遺伝子の数はいくつでもかまいません。このアプローチを使用すると、任意の順序の入力と出力でシステムをエンコードできます。その結果、これにより、任意のトポロジと任意の数のフィードバックで動的システムをエンコードできます。物理的な実行可能性のルールを遵守する必要があるだけです-エントリの順序は、出口の順序以下です。
このアプローチの欠点は、ダイナミクスの特性を制御することがより難しいことです。（3）と（4）を比較すると、（3）の各係数が（4）のいくつかの係数の組み合わせであることに気付くのは簡単です。したがって、最適なコントローラーの合成の観点からは、 GAのコンテキストでも（4）の形式でモデルレコードを使用する方が有益な場合があります。この場合、遺伝子には極の値またはFSのゼロが含まれ、この値は複雑になります。遺伝的プログラミングを使用した識別へのこのアプローチにより、集団内の個人の抵抗と最適な結果へのアルゴリズムの収束率の増加が期待されます。
PF記録形式の選択に関係なく、実数（または複素数）でエンコードを使用する場合、染色体は数字の配列になります。レベルごとに量子化を設定し、実数をバイナリ表現の整数に減らすことにより、バイナリコーディングを入力できます（「グレーコード」[2]）。ただし、伝達関数では、多くの場合、隣接する係数が数桁異なるため、精度に問題が生じる可能性があります。バイナリコーディングのもう1つの方法は対数（[2]も参照）で、最初の2ビットはべき関数の数と指数の符号をエンコードし、残りは指数自体の値をエンコードします。バイナリコーディングを使用すると、一方では複素数を使用するときにアルゴリズムが複雑になりますが、他方では、データのバイナリ表現を必要とする従来の遺伝演算子を使用できます。

フィットネス機能

GAの主要な概念の1つは、「フィットネス関数」または「フィットネス関数」の概念です。この個人が提示するソリューションがタスクの条件をどの程度満たしているかを示しています。最適なコントローラーを合成するタスクのコンテキストでは、規制の品質を個人の「適合性」を評価するための主要な基準として使用できます。移行プロセスのスムーズさとその継続時間の適切な組み合わせ。識別問題では、同じ効果に対する実際の（識別可能な）オブジェクトの反応に対する入力アクションに対するモデルの反応の近似の程度がより重要です。近似の程度は、識別可能なオブジェクトの記録された出力信号からモデルの反応の標準偏差を計算する平均二乗基準によって推定できます。この場合、フィットネス関数は分散計算式の形式になります。

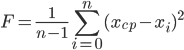（5）

式（5）で、nは識別可能なオブジェクトの記録された出力信号のサンプル数です。 x _cf-識別されたオブジェクトの出力信号からのこの個体の反応の偏差の算術平均。
個人の「フィットネス」を計算する手順は、次のようになります。まず、染色体をデコードする必要があります。暗号化された値を使用して、最初に連続伝達関数（連続時間を持つFS）を作成し、次にこのFSを使用して数値シミュレーションに便利な離散モデルを作成します。状態空間で離散モデルを使用するのが最も便利です[ 5 ]。
識別可能なオブジェクトの入力に適用されるものと同一の入力が、合成された離散モデルの入力に入力されます。この効果に対する個々の反応が記録されます。この場合、個体のモデルは、オブジェクトの出力信号の量子化周期に等しい時間の量子化周期でコンパイルされます。次に、式（5）を使用する必要があります。まず、オブジェクトの出力信号を記録して、結果の配列から配列要素を減算します。その後、適合度関数の値が高い個体がより適切であると見なされる場合、得られた分散で単位を除算できます。
さらに、適応度の低い関数（たとえば、べき乗則）をフィットネス関数に導入して、最も不適応な個人をよりゆっくりと選別することができます。これは適切なレベルで遺伝的多様性を維持するために行われなければなりません。個々の実行可能性チェックを追加することも必要です。以下の基準は、このような評価の基準として使用できます。

入口と出口の順序 -順序が多すぎるモデル、および入口の順序が出口の順序よりも大きいモデルは必要ありません。
移行プロセスの期間 -このモデルの参加によるシミュレーション（数値実験）を実行せずに、PPの時間を概算できます。 PPが長すぎる場合も、私たちには合いません。
オーバーシュート -最大反応と定常値の差と定常値の比;
振動 -ゆっくり減衰する自己振動のモデルは必要ありません。
安定性 -Hurwitz基準[4]を使用して簡単に決定できます。

交差と突然変異

出版物[2、p。134]は、単一点交差アルゴリズムについて説明しています。それは、染色体が「くっついて」おり、こうして得られた分岐を染色体間で交換する場所の選択にある。結果は2つの染色体であり、それぞれに両方の親からの遺伝子が含まれています。染色体ごとに1つの個体を作成することも、染色体の1つに対して1つの個体のみを作成することもできます。
同じ出版物では、マルチポイントクロスオーバー方法について説明しています。本質は同じままです-固着点が作成され、遺伝子鎖が再結合されます。違いは、遺伝子の可能な組み合わせの数、したがって、得られた結合染色体の数にあります。繰り返しますが、複数の個体を作成できます（染色体ごとにオプション）が、作成できるのは1人だけです。
遺伝子チェーン交換アルゴリズム自体は変更できます。値を単に置き換えるのではなく、 加重平均の計算を使用すると、遺伝子の競合の類似メカニズム（優性遺伝子と劣性遺伝子）が作成されます。唯一の違いは、遺伝子の優位性は個人の適応度によって決まるということです。
突然変異演算子は、ランダムに選択された遺伝子のランダムな値を計算するだけで実装できます。遺伝子の現在の値に対するランダムな増加を計算することも、 ビット反転を適用することもできます。最初の方法は望ましくありません、なぜなら伝達関数の係数の値は広範囲にわたって変化する可能性があり、1つの係数の値が非常に小さい値から大きい値に変化すると、フィットネス関数の値が急激に変化し、モデルの安定性が失われます。バイナリミューテーションにも同じ危険があります-数値の符号の原因となるビットの変更は、安定性の損失につながる可能性があります。したがって、この場合、遺伝子の現在の値に減少したランダムな増加を計算するためのアルゴリズムがより最適です。このアプローチは、乱数が選択される範囲が遺伝子の現在の値に比例することを意味します。比例係数は、いくつかの単位に等しいものを選択できます。

人口進化

[2]の211ページに、人口進化の擬似コードが示されています。

反復の各ステップで、標準の遺伝的プログラミング手順が母集団の個人に対して実行されます：適合度関数の計算、選択、交配、突然変異。人口全体の進化にとって、選択プロセスは重要な役割を果たします。それは、どのような速度で、そして一般的に集団が全体的に最適な状態に移行するのか、それとも極値にとどまるのかを決定します。いくつかのアプローチがあります。

ルーレットホイール -各個人はホイール上でセクターによって表され、その値は個人のフィットネス関数の値に比例します。
トーナメント方法 -人口はサブグループに分割され、その中でフィットネス関数の値に従って選択が行われます。
ランク法 -個人のフィットネス関数の値に応じて、ランクが割り当てられ、個人のランクが高いほど、そのコピーが次の反復ステップで母集団に入ることが少なくなります。
複合メソッド 。

フィットネス関数の最高値を持つ個人を偶発的な排除から保護するメカニズムを導入することが望ましいことに注意する必要があります。古典的な遺伝的アルゴリズムでは、適者が新しい母集団に入らない可能性がわずかにあります。したがって、フィットネス関数の最大値を持つ個人は、偶発的な除去から保護する必要があります。この戦略は「エリート主義者」と呼ばれます。
また、遺伝子操作を適用せずに一部の個人を新しい集団に移す戦略もあります。親は子孫の誕生直後に死ぬことはありません。この戦略に加えて、フィットネス関数に年齢ペナルティを導入できます。その値の減少は、個人の年齢に比例します。
GAのもう1つの重要な変更点は「ニッチ」です。それに応じて、最適化されたパラメータの多次元空間内の近傍の数と近接度に反比例する係数がフィットネス関数に追加されます。その結果、修正されたフィットネス関数は次のようになります。

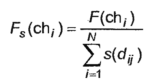（6）

個人がそのニッチに一人でいる場合、すなわちそれに類似した近傍が存在しない場合、フィットネス関数の値は変更されません。そうでない場合、その値は、ニッチ内の近接度と近隣の数に比例して減少します。さらに、近接度はさまざまな方法で推定できます。
ニッチの導入により、いくつかの極値を見つけることができます。複数の最適なモデルを一度に識別し、識別可能なオブジェクトにダイナミクス特性を近づけますが、同時に互いに異なります。

おわりに

結論として、現在、遺伝的アルゴリズムとさまざまな修正があり、そのうちのいくつかはこの記事で検討されており、進化戦略は1つの共通名「進化アルゴリズム」の下で組み合わされています。最初は、遺伝的アルゴリズムと進化戦略は互いに独立して開発されました。しかし、後に、専門家はこれら2つの分野の技術を組み合わせ始めました。現在、それらの違いはそれほど顕著ではありません。この記事で述べられていることの多くは、より正確に進化戦略に起因している可能性がありますが、認識を簡単にするために、すべてをそのままにしておくことにしました。

ご清聴ありがとうございました！あなたのコメント...

更新1：読者のリクエストに応じて、参照リストを展開します。

参照資料

1. ステファン・ウィンクラー、マイケル・アフフェンツェラー、ステファン・ワグナー 遺伝的プログラミング手法に基づいた非線形モデル構造の新しい識別方法//ヨハネスケプラー大学システム理論とシミュレーション研究所、オーストリア、リンツ{winkler、ma、sw} @ cast.uni-linz.ac.at
2. Rutkovskaya D.、Pilinsky M.、Rutkovsky L.ニューラルネットワーク、遺伝的アルゴリズムおよびファジーシステム：Trans。ポーランド語から。 I. D.ルディンスキー。 -M。：ホットライン-Telecom、2006 .-- 452 p .: Ill。
3. 動き「ボロノイ」
4. Routh-Hurwitz安定性基準
5. 状態空間（制御理論）
6. 遺伝的アルゴリズムの実用化の概念
7. 「Hello world！」遺伝的アルゴリズムの使用
8. 遺伝的アルゴリズム
9. 進化的アルゴリズム