Geekly Articles each Day

直接ファジー推論

はじめに


1965年、ジャーナル「Information and Control」は、L。Zadehの「Fuzzy sets」という題名の作品を出版しました。 この名前は、 ファジーセットとしてロシア語に翻訳されます 。 動機は、あいまいで不正確なそのような現象と概念を記述する必要性でした。 従来の集合論と2値論理を使用した既知の数学的手法では、このタイプの問題を解決できませんでした。



ファジーセットを使用すると、「高温」や「大都市」などの不正確で曖昧な概念を正式に定義できます。 ファジーセットの定義を定式化するには、いわゆる推論の領域を指定する必要があります。 たとえば、車の速度を評価する場合、X = [0、Vmax]の範囲に制限します。ここで、Vmaxは車が開発できる最高速度です。 Xは明確なセットであることに注意してください。

基本的な概念


空でない空間Xのファジーセット Aは、ペアのセットです。

どこで

-ファジーセットAのメンバーシップ関数。この関数は、各要素xにファジーセットAのメンバーシップの度合いを割り当てます。

前の例を続けて、3つの不正確な定式化を検討します。
-「車の低速」;
-「平均車両速度」;
-「高速車。」
図は、メンバーシップ関数を使用した上記の定式化に対応するファジーセットを示しています。

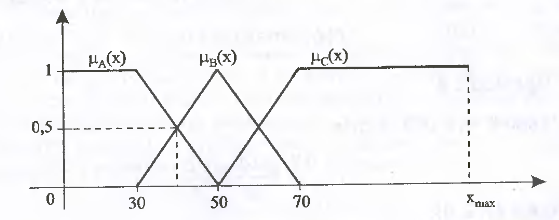
固定点では、X = 40km / h。 ファジーセット「低速車」のメンバーシップ関数の値は0.5です。 ファジーセット「平均車速」のメンバーシップ関数は同じ値を想定しますが、セット「高車速」の場合、この時点での関数の値は0です。

2つの変数Tの関数T：[0、1] x [0、1]-> [0、1]は、次の場合にTノルムと呼ばれます。
-両方の引数に関して増加していない：T（a、c）<T（b、d）a a <b、c <d;
-可換：T（a、b）= T（b、a）;
-接続条件を満たします：T（T（a、b）、c）= T（a、T（b、c））;
-境界条件を満たします：T（a、0）= 0、T（a、1）= a

直接ファジィ結論


ファジィ結論は、ファジィ前提から、おそらくファジィな結果が得られるプロセスとして理解されます。 おおよその推論は、自然言語を理解し、手書きを理解し、精神的な努力を必要とするゲームをプレイし、一般的に複雑で不完全に定義された環境で意思決定を行う能力の根底にあります。 定性的で不正確な用語で推論するこの能力は、人間の知能とコンピューターの知能を区別します。

従来の論理における推論の基本的なルールは、法則ポネン規則であり、それに従って文Bの真理を文AとA-> Bの真理で判断します。たとえば、Aが文「Stepanは宇宙飛行士」である場合、 「Stepanは宇宙飛行士である」および「Stepanが宇宙飛行士である場合、彼は宇宙に飛びます」という文があれば、「Stepanは宇宙に飛びます」という文も当てはまります。

ただし、従来のロジックとは異なり、ファジーロジックの主なツールは、モーダスポネンスルールではなく、いわゆる合成推論ルールであり、非常に特殊なケースはモーダスポネンスルールです。

曲線y = f（x）があり、値x = aが与えられていると仮定します。 次に、y = f（x）およびx = aであるという事実から、y = b = f（a）と結論付けることができます。

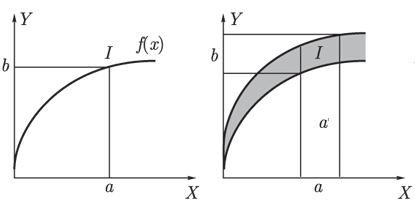
ここで、aが区間であり、f（x）が値が区間である関数であると仮定して、このプロセスを一般化します。 この場合、区間aに対応する区間y = bを見つけるために、まず基底aで集合aを構築し、値が区間である曲線との交点Iを見つけます。 次に、この交点をOY軸に投影し、間隔bの形式でyの目的の値を取得します。 したがって、y = f（x）およびx = AがOX軸のファジーサブセットであるという事実から、yの値をOY軸のファジーサブセットBとして取得します。

UとVを、それぞれベース変数uとvを持つ2つのユニバーサルセットとします。 AとFをUとU x Vの集合のファジーサブセットとします。その後、推論の合成規則は、ファジーセットAとFがファジーセットB = A * Fを意味すると述べています。

AとBをファジーステートメントとし、m（A）、m（B）を対応するメンバーシップ関数とします。 含意A-> Bは、メンバーシップ関数m（A-> B）に対応します。 従来のロジックとの類推により、

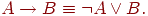
それから

ただし、これは含意演算子の唯一の一般化ではなく、他にもあります。

実装


直接ファジー推論方法を実装するには、含意演算子とTノルムを選択する必要があります。
開始Tノルムは最小関数です。
  1. def t_norm (v1, v2): return min (v1, v2)
  2. def t_norm (v1, v2): return min (v1, v2)

そして、ゲーデル関数が含意演算子になります：

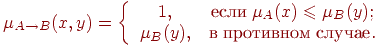
  1. def impl （v1、v2）：
  2. '' ' <br/> ゲーデルの含意 <br/> ' '' '
  3. v1 <= v2の場合 ：
  4. 1を 返します。 0
  5. その他 ：
  6. v2を返す

入力データには、次のような知識（ファジーセット）とルール（含意）が含まれます。
A = {（x1、0.0）、（x2、0.2）、（x3、0.7）、（x4、1.0）}。
B = {（x1、0.7）、（x2、0.4）、（x3、1.0）、（x4、0.1）}。
A =>B。

含意はデカルト行列の形式で提示され、その各要素は選択された含意演算子（この例ではGödel関数）を使用して計算されます。
  1. def compute_impl （set1、set2）：
  2. '' ' <br/> 計算の含意 <br/> ' '' '
  3. 関係= {}
  4. for i for set1.items（）：
  5. 関係[i] = {}
  6. set2.items（）のjの場合：
  7. v1 = set1.value（i）
  8. v2 = set2.value（j）
  9. 関係[i] [j] = impl（v1、v2）
  10. 関係を返す

上記のデータの場合：
結論：
A =>B。
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1

さらに、出力の結果として、新しいセットが取得されます。
  1. def 結論 （セット、関係）：
  2. '' ' <br/> 結論 <br/> ' ''
  3. conl_set = []
  4. 関係する iの場合：
  5. l = []
  6. 関係[i]のjの場合：
  7. v_set = set .value（i）
  8. v_impl =関係[i] [j]
  9. l.append（t_norm（v_set、v_impl））
  10. 値= 最大 （l）
  11. conl_set.append（（i、value））
  12. conl_setを返します

結果：
B '= {（x1、1.0）、（x2、0.7）、（x3、1.0）、（x4、0.7）}。

ソース


Source: https://habr.com/ru/post/J111187/

More articles:


All Articles