Geekly Articles each Day

モノイドとその応用：木でのモノイド計算

ご挨拶、Habrahabr。 今日、私はいつものスタイルで、コミュニティにデータ構造に関する小さな教育プログラムを提供したいと思っています。 今回だけ、より包括的になり、そのアプリケーションと実用性は、プログラミングの最も多様な分野にまで広がります。 もちろん、最も美しいアプリケーションについては、記事で直接示して説明します。

抽象的思考のドロップ、バランスのとれた検索ツリー（たとえば、前述のデカルトツリー ）の知識、単純なC＃コードの読み取り能力、得られた知識を適用したいという欲求が必要です。

そのため、今日の議題には、 モノイドと、計算をツリーにキャッシュするための主なアプリケーションがあります。

概念としてのモノイド


多数のもの 、つまり操作する多数のオブジェクトを想像してください。 Mと呼びましょう。 このセットでは、バイナリ演算、つまり、新しい要素をセットの要素のペアに関連付ける関数を導入します。 以下、この抽象操作を「⊗」で表し、式を中置形式で記述します。aとbがセットの要素である場合、 c = a⊗bもこのセットの要素です。

たとえば、世界に存在するすべての線を考えてみましょう。 また、文字列連結操作について考えてみ"JohnDoe" 。これは、数学では伝統的に「◦」と呼ばれ、ほとんどのプログラミング言語では「+」： "John" ◦ "Doe" = "JohnDoe"です。 ここで、セットMは文字列であり、◦オペレーションasとして機能します。
または、タプルを操作するときに関数型言語で知られているfst関数もあります。 彼女は2つの引数のうち、結果として最初の引数を順番に返します。 したがって、 fst （ 5、2 ）= 5 ; fst （ "foo" 、 "bar" ）= "foo" 。 この2項演算をどのセットで考慮するかは問題ではないため、いずれを選択するかはユーザーの選択です。

次に、操作「⊗」に結合性制約を課します。 これは、以下を必要とすることを意味します。「⊗」を使用する場合、オブジェクトのシーケンスが結合されると、「⊗」の適用順序に関係なく、結果は同じままになります。 より厳密には、 任意の 3つのオブジェクトa 、 b 、およびcについて、次のようになります。
（a⊗b）⊗c = a⊗（b⊗c）
文字列の連結が連想的であることは簡単にわかります。文字列シーケンスのどの接着が先に行われ、後でどの接着が行われても、シーケンス内のすべての文字列の共通の接着が得られます。 同じことが関数fstにも当てはまります。
fst （ fst （ a 、 b ）、 c ）= a
fst （ a 、 fst （ b 、 c ））= a
シーケンスへのfstアプリケーションのチェーンは、任意の順序で引き続きヘッド要素を生成します。

そして最後に必要なことは、操作に関する集合Mには、 中立要素または操作単位が存在する必要があることです。 これは、セットの任意の要素と組み合わせることができるオブジェクトであり、セットを変更することはありません。 正式に言えば、 eが中立要素である場合、セットのaについては 、
a⊗e = e⊗a = a
線のある例では、ニュートラル要素は空の線""です。どちらの線に貼り付けても、線は変わりません。 しかし、この点でのfstは私たちに適しています。中立的な要素を考え出すことは不可能です。 実際、 fst （ e 、 a ）= eは常にeであり、 a ≠ eの場合、中立性は失われます。 もちろん、1つの要素のセットでfstを検討できますが、そのような退屈を必要とするのは誰ですか？ :)

そのような各トリプル<M、⊗、e>は、 モノイドと厳soleに呼ばれます。 コードでこの知識を修正します。
 public interface IMonoid<T> { T Zero { get; } T Append(T a, T b); }

モノイドのより多くの例、および実際にそれらを使用する場所は、カットの下にあります。


例



先に進む前に、読者に世界に闇があり、さまざまなモノイドをあいまいにしていることを納得させる必要があります。 そのうちのいくつかをテキストの後半で例として使用しますが、実際には読者が遭遇するものもあります。 各モノイドに対して、問題のセット、組み合わせ操作、ニュートラル要素を示す簡単なリストを作成します。 すべての操作の関連性をご自身で確認してください。ここには十分なスペースがありません。さらに、少しカンニングします。また、次の記事では章全体を取り上げるので、最も興味深い、異常なモノイドをリストに含めません。

したがって、人気のあるモノイド：

これについては、今すぐ（！）例を終了して練習に移りましょう。 この待望のプラクティスを実際に紹介する前に、このリストからいくつかの単純なモノイドの定義をC＃で記述します。これについては次の章で扱います。
すべてのモノイドをシングルトーンとして実装します。 後で不明なモノイドタイプのインスタンスにアクセスしやすくするために、その作成を別の静的クラスに入れました。

 public static class Singleton<T> where T : new() { private static readonly T _instance = new T(); public static T Instance { get { return _instance; } } } public class AddMonoid : IMonoid<int> { public AddMonoid() {} public int Zero { get { return 0; } } public int Append(int a, int b) { return a + b; } } public class FunctionMonoid<T> : IMonoid<Func<T, T>> { public FunctionMonoid() {} public Func<T, T> Zero { get { return x => x; } } public Func<T, T> Append(Func<T, T> f, Func<T, T> g) { return x => g(f(x)); } } public class GCDMonoid : IMonoid<int> { public GCDMonoid() {} private int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } public int Zero { get { return 0; } } public int Append(int a, int b) { return gcd(a, b); } }


コンピュータサイエンスのどこでロープ



この瞬間から、私たちは実用的なアプリケーションの分野に入ります。

まず、 Ropeというデータ構造定義が必要です。 まれなロシア語の情報源は、苦労せずにそれをロープのように翻訳します。私はこの伝統から引き下げません。 したがって、ロープは、追加機能を備えた不変文字列の便利な実装として、1995年に最初に提案されました。たとえば、部分文字列を取得して文字列をマージする非常に高速な操作です。 このような目的のために、この構造は、たとえばJavaライブラリで引き続き使用されます。

任意の平衡二分木を想像してください。 このツリーの葉として言葉を掛けます-つまり 文字の配列。 結果のツリーは、たとえば次のようになります。

このようなデータ構造はロープと呼ばれます。

インデックスアクセス

デカルトツリーに関する以前の記事から、このようなツリーでインデックスによるシンボルクエリの決定がどのように可能かを覚えています-サブツリーを中間頂点に格納するだけで十分です。この場合、サブツリーから中断された文字列の全長です。 このツリーの場合、同様のスキームは次のようになります。

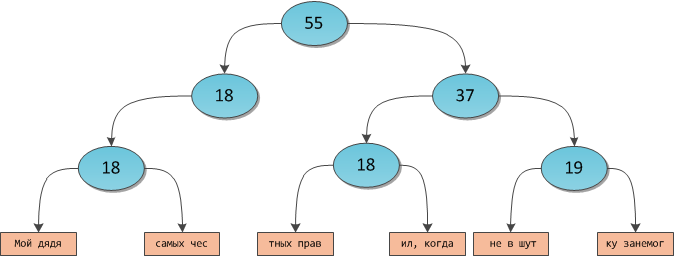
ここで、K番目の順序統計の使い慣れたアルゴリズムを使用して、目的の番号の下の文字を含む配列に移動し、配列のメモリ内で直接インデックスを作成して目的の文字を返すことができます。 大きな行でのメモリ最適化と小さな行でのパフォーマンスの理由だけで、個々の文字ではなくツリーの葉で配列が中断されていることに注意してください。

接着

2本のロープを接着するには、新しいルート頂点を作成し、2つのデータツリーを息子としてサスペンドするだけで十分です。 ソースツリーのバランスが取れているため、新しいロープもバランスが取れます。 彼らはまた、接着されたロープが小さすぎるかどうか、結果として得られるロープでいくつかのリーフセグメントを組み合わせることが理にかなっているかどうかをよく調べます。

部分文字列リクエスト

文字列内の部分文字列を選択するには、K番目の順序統計に類似した単純なアルゴリズムを適用するだけで十分です。 ロープTの開始文字から始まる長さlenの部分文字列を選択する必要があるとします。

最初に、2つの極端なケースを考えます。
start = 0かつlen = T.Left.Size場合、答えはT.Leftサブツリー全体T.Left 。 同様に、 start = T.Left.Size 、およびlen = T.Right.Size場合、答えはT.Rightサブツリー全体T.Right 。 上の図では、2番目のケースはSubstring( start : 18, len : 37)関数Substring( start : 18, len : 37)を呼び出すと実現され、関数は必要な部分文字列" , "正しいサブツリーをすぐに返します。

さらに、目的の部分文字列が完全に左のサブツリーにある場合、つまりstart < T.Left.Sizeでstart + len ≤ T.Left.Size start < T.Left.Sizeの場合も可能start + len ≤ T.Left.Size 。 次に、左のサブツリーに対してサブストリング検索関数を再帰的に呼び出す必要があります。
対称の場合は、完全に右側のサブツリーにある部分文字列です。つまり、 start ≥ T.Left.Size 、 start + len ≤ T.Left.Size + T.Right.Sizeです。 次に、再帰検索は右のサブツリーに進みます。左のサブツリーのサイズをstartから減算することを忘れないでください。結局、右のサブツリーのインデックス作成はゼロから始まり、独立したツリーと見なされます。
この例では、 Substring( start : 18, len : 18)呼び出すことができます。 次に、最初のステップで、関数は再帰的に右にSubstring( start : 0, len : 18)て、右のサブツリーSubstring( start : 0, len : 18)を呼び出す必要があると判断します。 そして、彼は、最初のケースに従って、 " , "部分文字列に対応する、彼の左のサブツリー全体を返し" , " 。

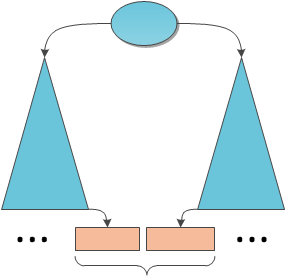
そして最後に、最もトリッキーなケース-目的の部分文字列が左右のサブツリーの一部に重なります。
この場合、左のサブツリーにのみ入るピースを選択し、次に右のサブツリーに入るピースを選択して、それらをマージする必要があります。 2本のロープを結合する方法はすでに知っています。
希望するピースのインデックスを決定することはまったく難しくありません。 左サブツリーの再帰呼び出し：
Substring( start : start, len : T.Left.Size - start)
右の場合：
Substring( start : 0, len : len - (T.Left.Size - start)) 。
繰り返しますが、右のサブツリーにゼロをstart引数として渡す必要がありました。そのサブツリーの関数は独立して動作するためです。
これらのインデックスが明らかでない場合は、図を見てください。

最終的に、再帰呼び出しは、サブストリング要求がすでにセグメントに沿って通常の線形方法で行われているリーフに到達します。 これにより、最大のパフォーマンスが保証されます。 操作の合計複雑度はO（log N）です。

その他

このようなデータ構造は、文字列の実装だけでなく使用できると言う必要はないと思います。 要素の巨大なシーケンスは、同様の形式で表すことができます。基礎となるリーフセグメントに最適な長さを選択するだけで十分です。 -巨大な長さの不変のシーケンスを操作するための便利なデータ構造を取得します。 確かに、これまでのところ、そのような移行の説得力のある議論として役立つ十分な操作が実証されていません。 何も、それは修正可能です:)

構造の選択に関して。 データをリーフに保存する任意の自己バランス型バイナリツリー（たとえば2-3ツリーまたはB ツリー）を選択できます。 主にセットの実装用に作成された多くの検索ツリーは、 赤黒ツリーやデカルトツリーなど、各頂点にデータを保存します。 それらに文字列行を実装することは実用的ではありません。これにより、操作中に大量のメモリ割り当てが発生し、コードがやや複雑になりますが、この記事の主なタスクであるモノイドを持つツリーのパラメーター化は、第1および第2のツリーの両方に簡単に適しています したがって、ストーリーの過程で、プレゼンテーションを容易にし、さまざまなバランスの取れたツリーの実現の詳細で混乱しないように、時にはデカルトツリーに関する記事のテキストを参照し、時にはフィンガーツリーを参照します。これは完全に不要です。 読者があらゆるアプローチを完全に理解し、受け入れることを願っています。


パラメータ化、またはツリーの測定方法



デカルトツリーの例を使用して、サブセグメントで複数のクエリを作成した方法を思い出してください。 手短に言えば、この概念の本質を思い出させてください。ツリーの各頂点に特定の注釈が保存されました。その頂点にルートを持つサブツリーに対応するサブセグメントの要求値に等しいパラメーターです。 たとえば、サブツリー要素の合計、サブツリー要素の最大値、サブセグメント上のブールフラグの有無などです。 ユーザーがサブセグメントでリクエストを行いたい場合、一部のサブツリーでは回答がすでに頂点にキャッシュされており、それらを結合するためにのみ残っているため、探しているすべての頂点に対してO（N）として毎回再計算する必要はありませんでした

デカルトツリーでは、各頂点で正義を復元するためのすべての「ブラックワーク」はSplit関数によって行われました。必要なサブセグメントをツリーから切り取り、ルートの計算値をリクエストへの応答として取得するだけで済みました。 しかし、別の方法で行うこともできます。 ロープで部分文字列を取得するアルゴリズムを覚えていますか？ 彼は上から下に再帰的に下降し、目的の部分文字列の左右の境界をローカライズし、途中で見つけたものをすべてマージしました。 このアプローチはここで完全に適用できます。

頂点にある注釈付きの暗黙的なデカルトツリー-サブツリーの合計-を再度検討し、サブセグメントの合計をクエリしようとします[4; 8] [4; 8] 。

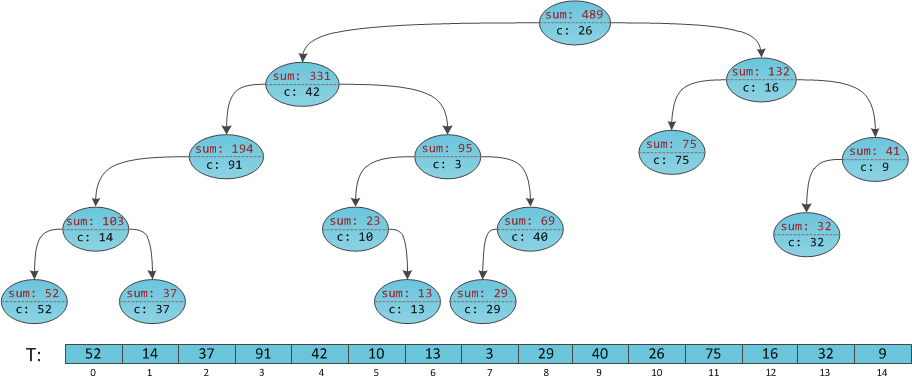
結果を0に初期化します。
反復1では、左のサブツリー[0; 9]。 結果は0のままです。
反復2では、右のサブツリー[5; 9]。 結果は、ルートの値-42で増加します。
反復3では、右のサブツリー[8; 9]。 結果は、左のサブツリーの合計[5; 6]にルートの値を加えて、42 + 23 + 3 = 68になります。
反復4では、左のサブツリー[8; 8]。 結果は68のままです。
反復5では、結果に（29）のルートの値を追加し、合計97を取得します。これが問題の答えです。

スキームは、各頂点でよく知られているケース分析に基づいて非常に単純です。要求されたセグメントは、左息子、右息子、および自分に対応するセグメントとどのように対応しますか？ これに基づいて、左右のサブセグメントの値を計算して合計する1つまたは2つの再帰呼び出しを行います（上記の例では、2つの再帰呼び出しは必要ありませんでした）。 場合の分析で今だけはまだルートに保存されたデータを考慮する必要があります。

葉の上部と上部にサブセグメントの合計に対応する注釈が格納されているロープを簡単に想像できます。 次に、サブセグメントの金額のリクエストは、前の段落からサブストリングを取得するアルゴリズムと構造が同じで、この金額を累積し、再帰から戻る-結果に答えを追加し、より高い値を渡します。 スキームの単純さは疑いの余地がありません。なぜ正しい答えが常に得られるのかを理解したいだけです。

これを理解するのも簡単です。 実際、単純にサブセグメントのすべてのセルを直線的にたどったのと同じ合計を実行します。ここでは、a）セルのブロック全体のみを要約します。 b）必ずしも左から右の順序ではありません。 実際、次のようなプロセスを想像できます。
行パス：（C l + C l + 1 + ... + C r ）
ツリー要求：（C l +（（（C l + 1 + ... + C i ）+（C i + 1 + ... + C j ））+（C j + 1 + ... + C r-1 ）+ ... + C r ））
実際には、単に他の順序でブラケットを配置しますが、これは結果を変更するものではありません。「+」は連想操作であるためです。 ああ、私は最初の段落からおなじみの言葉に出会った:)もっと一般的な概念がここでつつかれているようだ...

測定する

ツリーに含まれる一連の要素を特徴付ける関数を、ツリーの尺度と呼びます。 通常、ツリーメジャーは、後でクエリを実行する操作です。要素の合計、要素の最大値、要素上のフラグの存在など、すでに例を示しています。たとえば、平方和や文字の頻度のヒストグラムなど、より複雑な測定値を想像できます。

すでに知られている手法を使用して、どのメジャーも各サブツリーのロープの上部にキャッシュできます。次に、測定関数が結合的である場合、上記のアルゴリズムによる任意のサブセグメントの測定要求を対数時間で簡単に実行できます。このプロパティに、ツリーの個々の要素のメジャーを決定する機能の完全に論理的な要件を追加します。

普遍的なデータ構造、つまりロープを取得します。これにより、ロープの接着や切断後など、サブセクションのメジャーの値をすばやく照会できます。ツリーはそれ自体でバランスが取れているため、アクセス時間は対数のままです！要素を追加すると、新しいサブツリーのキャッシュされたメジャー値が再計算され、未変更のサブツリーは同じままになります。 Oのすべて（log N）。素晴らしい。

さて、メジャーの定義を少し絞りましょう。ツリーの各具体的な単一要素のみを測定する方法を教えてください。今サブツリーの測定値を取得する方法は？とても簡単です。1つの要素の測定値と他の要素の測定値の組み合わせが、それらの2つのセットの測定値を与えるように、2つの測定値を互いに組み合わせることができれば十分です。同時に、この結合プロセスは連想的である必要があります。そうしないと、クエリアルゴリズムが誤った答えを受け取ります。これらの考慮事項により、自然な結論に至ります。測定値は任意の関数であり、その結果はモノイドの要素です。

「最大」メジャーは、モノイド<Numbers、max、-∞>の結果を持つxの基本関数です。
「二乗和」メジャーは、モノイド<Numbers、+、0>の結果を持つ基本関数x 2です。
測定「周波数ヒストグラム」-基本関数「単一の指定されたシンボルに対して100％」結果はモノイド<ヒストグラム、文字数を考慮したヒストグラム、空のヒストグラムを組み合わせたもの>になります。読者は、演習として、頻度ヒストグラムを結合する完全に関連する操作を検討する必要があります。

ここで達成したことをコードで説明します。これからは、C＃での同じアイデアの実装が非常にugく多音節に見えるため、Haskellに完全に切り替えるとよいでしょう。たとえば、ツリーは2つではなく3つの典型的なパラメーターでパラメーター化する必要があります！
バランスを取ることなく、実際に追加/接着/切断することなく、単純なバイナリツリーの実装を提供します。これらの操作がどのように実装されるかは、特定のタイプのバランスのとれたツリーごとに固有であり、別の記事が必要になりますが、これは私の目標ではありません。読者は簡単にクラスの代わりに想像することができますTree例えば、FingerTree。または、ImplicitTreap「正義の回復」の対応する機能が書き直され、データがツリーの頂点にも保存され、ツリーの頂点の子孫もヌルになる可能性があることを考慮した、やや複雑なもの。
 //  ,   . public interface IMeasured<V> { V Measure { get; } } //  :      public class IdentityMeasure<T> : IMeasured<T> { public readonly T Data; public IdentityMeasure(T data) { Data = data; } public T Measure { get { return Data; } } } // T -      // V -      // M - ,         public class Tree<T, M, V> : IMeasured<V> where M: IMonoid<V>, new() where T: IMeasured<V> { public readonly T Data; //    public readonly Tree<T, M, V> Left; public readonly Tree<T, M, V> Right; private readonly V _measure; public V Measure { get { return _measure; } } public Tree(T data) //   { Left = Right = null; Data = data; _measure = data.Measure; } public Tree(Tree<T, M, V> left, Tree<T, M, V> right) //   { Left = left; Right = right; Data = default(T); _measure = Singleton<M>.Instance.Append(left.Measure, right.Measure); } } //  ,      public class SumTree : Tree<IdentityMeasure<int>, AddMonoid, int> { public SumTree(int data) //   : base(new IdentityMeasure<int>(data)) {} public SumTree(SumTree left, SumTree right) //   : base(left, right) {} } //  ,      public class PriorityTree : Tree<IdentityMeasure<double>, MaxMonoid, double> { public PriorityTree(double data) //   : base(new IdentityMeasure<double>(data)) {} public PriorityTree(PriorityTree left, PriorityTree right) //   : base(left, right) {} }


このセクションのすべての努力の集大成は、サブトリム測定を要求するための一般化された方法になります。
 //  . //      : Size = 1 + left.Size + right.Size; public readonly int Size = 1; public V MeasureOn(int start, int length) { if (start == 0 && length == Left.Size) return Left.Measure; if (start == Left.Size && length == Right.Size) return Right.Measure; if (start + length <= Left.Size) return Left.MeasureOn(start, length); if (start >= Left.Size) return Right.MeasureOn(start - Left.Size, length); var monoidV = Singleton<M>.Instance; var leftValue = Left.MeasureOn(start, Left.Size - start); var rightValue = Right.MeasureOn(0, length - (Left.Size - start)); return monoidV.Append(leftValue, rightValue); }


新しいステージ：述語


モノイドによってパラメーター化されたロープに対して実行できる操作のクラスをさらに拡張できます。サブセグメントに関するさまざまな対策の要求を満たす方法をすでに知っています。しかし、人生ではしばしば、特定の意味を知ることだけでなく、その創造に「主に」関与する要素も必要です。

たとえば、メジャーがセグメント内の要素の最大値である場合、このアカウントがこの最大値に達する特定の要素を知ると便利です。古い良好なインデックスアクセスは、同じ操作にも適用されます。思い出すように、これらの操作はすべて非常によく似たアルゴリズムで記述されています。これは、ツリーの頂点から目的のリーフに到達するまで、頂点から直線に下降します。したがって、このようなすべての操作を一般化する非常に簡単な方法があります。

いくつかの述語 pを考えます、つまり、1つの任意の引数のブール関数。
我々は、オブジェクトの配列を有するましょう1 ... Nのを。オブジェクトは、ある種のモノイドの要素です。たとえば、行にします。シーケンスのプレフィックス合計を順次計算します。これは、この新しいシーケンスです：1 1 ⊗ 2 1 ⊗ 2 ⊗ 3





...
1 ⊗ 2 ⊗ 3 ⊗···⊗ Nのところ「⊗」、我々は、合意した-モノイドの操作を。文字列を使用した例では、連結になります。ここで、これらのすべてのプレフィックスの合計について述語の値を計算します。ブール値のシーケンスを取得します。そして最後に、接頭辞の和で常にFalseである場合、述語モノトーンを呼び出し、ある時点でFalseをTrueに変更し、その後シーケンスの最後までTrueのままになります。簡単に言えば、Falseを0に、Trueを1に置き換えると、述部の結果のシーケンスは減少しないはずです。






モノイド文字列の図でこのプロパティを示します。ましょうP（S）= { sが含ま""ストリングとして}。
ロープの上部には、メジャー値、つまりサブツリーラインの連結がキャッシュされています。

アルゴリズムは常に2つのプレフィックスをサポートしています。1つは現在の左の息子を考慮せず、もう1つはそれを含めます。これらのプレフィックスの述語の値に応じて、どのサブツリー内で「ジャンプ」が発生したかを常に正確に判断できます。
たとえば、ロープのルートにいるとき、アルゴリズムはp（" "）= Falseを検出しました。これは、ジャンプが右のサブツリーで発生したことを意味します。しかし、次の反復では、左接頭辞pの値（" , "）= Trueであるため、左のサブツリーに移動する必要があります。

降下中、プレフィックスの正しい値を常に維持し、右サブツリーへの降下の場合、現在の左の息子の尺度でそれを接着する必要があります。

最終的に、対数のステップで、ジャンプが発生したシートに到達します。リーフセグメントの内部では、別の方法で正確なジャンプ位置を探す必要があります。ほとんどの場合、順次チェックが必要です。ただし、これはささいなことではないかもしれません。「特定の部分文字列を含む」述語の代わりに、「特定の正規表現を満たす」述語を想像してください。また、単調ですが、計算には多少の労力が必要です。

たとえば、「平方の合計」という形式と「256を超える」述語のメジャーの場合、ジャンプの正確な位置を決定するために、シート内のセグメントから特定の各数値の平方を個別に計算する必要もあります。

ところで。単語を含むセグメントではなく、シート内の文字を別々に保存する場合、このアルゴリズムに基づいて、分割操作を決定できます。単調な述語に従ってツリーを2つにカットします。左側の結果では、述語プロパティはまだ満たされておらず、右側では、すでに満たされています。正確な分割アルゴリズムの実装は、演習として読者に明確な良心を委ねることができます:)
ところで、次の段落の1つでは、それはまだ有用です。
, . , . .


しかし、たとえば、インデックスiを持つ要素へのアクセスは、単調な述語「prefix length> i」を使用したツリー内の単なる検索であることは明らかです。プレフィックスの長さは通常の尺度であり、頂点にサブツリーのサイズを格納する際の尺度として使用しました。この測定では、基本関数は単位単位であり、値はモノイド<Numbers、+、0>にあります。位置番号i-これは、シーケンスプレフィックスの長さがiを超え始める位置です。

選択された例



そこで、モノイドを使ったロープのパラメーター化などの概念がもたらす主な利点をすべて調べました。「測定可能な」値の任意のシーケンスを取得し、結果のシーケンスのサブセグメントに対して、メジャーの値を認識して、それらを次々に結合できます。興味がある場合は、単調な述語に従って結果のロープを切断することで、達成の正確な位置を見つけることができます。そして、これらすべてを対数時間で行い、可能性の範囲を無限にします。この無制限のスコープを今すぐ実行して、3つのかなり標準的ではない、非常に重要で興味深いモノイドを紹介します。

例1：統計


今回は、退屈な数字、文字列、ブールよりも退屈なものを操作しています。私たちの細心の注意の対象は...サンプルです。

サンプル、つまり特定の母集団からの有限なランダム値のセットが測定可能です。誰もがサンプルの主な特徴を知っています：
N-サンプルサイズ。
Mはサンプルの平均値です。
Vは標本の分散、つまり、平均標本からの偏差の二乗の平均値です。スケーリングされていない分散、つまり、単に平均からの偏差の二乗の合計
を考慮します。必要であれば、これは単純に数割る、基本かもしれそれから抜け出すNのを。



下の段落で、サンプルは「測定可能」であると述べました。はい、この言葉を誤って使用したことはありませんでした:)サンプルのこれら3つの基本的な特性のセットが、その尺度として役立ちます。
ストップ-ストップ-ストップ、あなたは言う、3つの疎結合された数の同じセットは何ですか-モノイドの要素ですか？それはどんなモノイドですか？どういうわけかサンプルを結合する必要があります、それが判明しますしかし、どうですか？

これはすべて美しく行われます。同じ母集団からの2つのサンプルAとBがあるとします。これらのサンプルをマージして、共同サンプルXを作成します。このサイズは、元のサンプルのサイズの合計です。その後、1979年にトニーチャンが示したように、新しいサンプルの平均およびスケールなしの分散は、次の式を使用して計算できます。




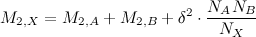明らかに、サンプルをどの順序で混合するかは重要ではありません。最終サンプルの特性は同じです。したがって、サンプルのマージは結合的です。
空のサンプルの特性が何であるかを判断するのは、形式的なままです。そのサイズは明らかに0であり、相加性による平均も0になりますが、分散を十分に決定することはできません。ただし、必要はありません。ツリーでは、空のサンプルの分散にまったく触れません。

統計的特徴のモノイドとそれに続くすべての定義をpastie.orgに定義する必要がありました。これは、記事のサイズに対するHabrahabrの制限がやや緊張し始めるためです:)

サイズKの「ウィンドウ」が移動するランダム変数のストリーム、つまり 最後のK個の量の分散と期待値を常に知る必要があります。ツリーが作成され、要素がキューから順次削除されて追加され、必要な計算値は常にツリーのルートにあります。美人

例2：画像のアルファ合成


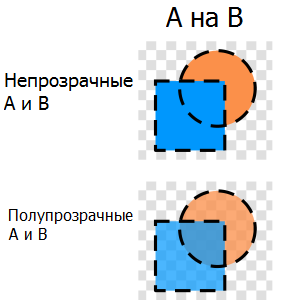2つの半透明の画像があります（アルファチャネル付き）。アルファ合成として知られている2つの画像のオーバーレイ演算子を定義します。Photoshopで半透明の画像を使用したことがある人は誰でも、その動作に精通しています。画像の各ピクセルには、カラーCとアルファチャネルαの 2つのパラメーターが定義されています。これらの値を計算するための式を完全に明確に定義すると、重ね合わせ演算子が定義されます。したがって、次の事実は数学的に簡単に導き出せることがわかります。



これらの事実と特定の公式の証明については、対応するウィキペディアの記事を参照してください。

したがって、アルファ合成の動作の半透明の画像はモノイドを形成します。これにより、適切なツリーを使用して、互いに重ね合わせる必要がある巨大な画像のセットを処理する機会が与えられます。

例3：正規表現

残念ながら、Habrahabrによって記事に課されたボリュームは、私がそれを知的に仕上げることができず、3番目の美しいモノイド、すなわち正規表現を認識するための有限オートマトンの遷移関数のモノイドを詳細に説明することはできません。これをロープで使用すると、インクリメンタルレクサーを作成できます。これは、行をすばやく変更し、指定された正規表現が前の行と一致する場合にいつでも即座に答えを出すことができる構造です。詳細については、Dan Piponi による元の記事の翻訳と、より詳細な記事である Eugene Kirpichevの実装を参照してください。播種画像：


それまでの間、ご清聴ありがとうございました。

Source: https://habr.com/ru/post/J112394/

More articles:


All Articles