Pythonとグラフの実装

Magnus Lie HetlandのPython Algorithmsから最も興味深い章を発行し続けています。 前の記事はhabrahabr.ru/blogs/algorithm/111858にあります。 今日は、グラフとツリーの効率的な作業と、Pythonでのそれらの実装の機能に焦点を当てます。 グラフ理論の基本的な用語はすでに説明されているため（たとえば、ここ： habrahabr.ru/blogs/algorithm/65367 ）、この記事では用語に関する章の一部を含めていません。

グラフとツリーの実装

たとえば、最短ルートに沿ってポイントを移動する問題など、多くのタスクは、 グラフを使用して最も強力なツールの1つを使用して解決できます 。 多くの場合、グラフの問題を解決していると判断できれば、少なくとも解決策の半分になっています。 また、データを何らかの形でツリーとして表現できる場合、真に効果的なソリューションを構築するあらゆる機会があります。
グラフは、トランスポートネットワークからデータ伝送ネットワークまで、細胞核内のタンパク質の相互作用からインターネット上の人々のつながりまで、あらゆる構造またはシステムを表すことができます。

重みや距離などのデータを追加すると、グラフがさらに便利になります。これにより、チェスをしたり、能力に応じて人の適切な仕事を決定するなど、さまざまな問題を説明できます。
ツリーは特別な種類のグラフであるため、ほとんどのグラフアルゴリズムと表現はそれらに対しても機能します。
ただし、特殊な特性（接続性とサイクルの不足）により、アルゴリズム（および表現）の特殊な（非常に単純な）バージョンを使用することが可能です。
実際には、場合によっては、ツリー形式で表現できる構造（XMLドキュメントやディレクトリ階層など）があります（IDREF属性とシンボリックリンクを考慮に入れると、XMLドキュメントとディレクトリ階層はグラフになります）。 実際、これらの「一部の」ケースは非常に一般的です。

グラフに関する問題の説明はかなり抽象的なため、ソリューションを実装する必要がある場合は、グラフをデータ構造として表す必要があります。 （これは、アルゴリズムを設計するときにも行う必要があります。これは、グラフ表現でさまざまな操作が実行される時間を知る必要があるためです）。 場合によっては、グラフはすでにコードまたはデータで作成されているため、別の構造は必要ありません。 たとえば、リンクを介してサイトに関する情報を収集するWebクローラーを記述する場合、グラフはネットワーク自体になります。 friends属性（ Person型の他のオブジェクトのリスト）を持つPersonクラスがある場合、オブジェクトモデルは既にさまざまなアルゴリズムを使用できるグラフになります。 ただし、グラフを表す特別な方法があります。

一般的には、 N [v]が vに隣接する頂点のコレクション（または場合によっては反復子）になるように、隣接関数N（v）を実装する方法を探しています。 他の多くの本と同様に、最も有用で一般化されているため、2つの最もよく知られている表現、 隣接リストと隣接マトリックスに焦点を当てます 。 代替表現については、以下の最後のセクションで説明します。

ブラックボックス：辞書とセット

 ,       ,      Python,  — <em></em>.      (   ),    .      , ,     (  ,      ).     Python   hash: >>> hash(42) 42 >>> hash("Hello, world!") -1886531940     ,     -.     .    ,           (    -,       ).     ,           Θ(1). (     Θ(n),            -.    ,     ).    ,      dict  set    ,                . 

隣接リストなど

グラフを表す最も明白な方法の1つは、隣接リストです。 その意味は、各頂点について、それに隣接する頂点のリスト（またはセット、別のコンテナ、イテレータ）が作成されるということです。 0 ... n-1と番号付けられたn個の頂点があると仮定して、そのようなリストを実装する最も簡単な方法を分析しましょう。

  ,            .       0… n-1     ,           . 

したがって、各隣接リストはそのような番号のリストであり、これらのリスト自体は、頂点番号でインデックス付けされたサイズnのメインリストに収集されます。 通常、そのようなリストのソートはランダムであるため、私たちが話しているのは、隣接セットを実装するためのリストの使用です。 用語リストは、単に歴史的に確立されたものです。 幸いなことに、Pythonにはセット用の別のタイプがあり、多くの場合、使いやすいです。

さまざまな表現が表示されるグラフの例を図に示します。 1.まず、すべての頂点に番号が付けられていると仮定します（ a = 0、b = 1、... ）。 これを念頭に置いて、次のリストに示すように、グラフを明白な方法で表すことができます。 便宜上、図の頂点ラベルに従って名前が付けられた変数に頂点番号を割り当てました。 ただし、数値を直接操作できます。 どのトップがどのリストに属するかは、コメントに示されています。 必要に応じて、ビューが写真と一致することを確認するために数分かかります。

 a, b, c, d, e, f, g, h = range(8) N = [ {b, c, d, e, f}, # a {c, e}, # b {d}, # c {e}, # d {f}, # e {c, g, h}, # f {f, h}, # g {f, g} # h ] 

   Python  2.7 ( 3.0)     set([1, 2, 3])  {1, 2, 3}.       -   set(),   {}   . 

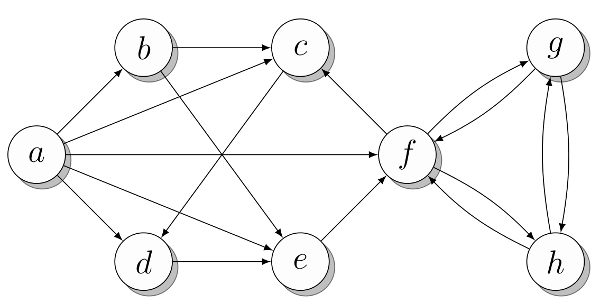
図 1.さまざまな種類のプレゼンテーションを示すおおよそのグラフ

リストの名前Nは、上記の関数Nに関連付けられています。 グラフ理論では、 N（v）はvに隣接する頂点のセットを表します。 同様に、このコードでは、 N [v]はvに隣接する頂点のセットです。 Nが上記の例のように定義されていると仮定すると、Python対話モードでこのビューを探索できます。

 >>> b in N[a] # ? True >>> len(N[f]) #  3 

 :        , ,     ,         ,    ,    python   -i,  : python -i listing_2_1.py          ,      ,     ,       . 

別の考えられるビューは、場合によってはオーバーヘッドが少なくなりますが、隣接リスト自体です。 そのようなリストの例を、以下のリストに示します。 すべて同じ操作が利用可能ですが、頂点隣接チェックはΘ（n）で実行されます。 これにより、速度が大幅に低下しますが、このプレゼンテーションが本当に必要な場合は、これが彼の唯一の問題です。 （アルゴリズムが行うことはすべて、隣接する頂点をバイパスすることである場合、タイプセットのオブジェクトを使用することは無意味ではありません：オーバーヘッドは、実装の漸近的動作における一定の要因を悪化させる可能性があります）。

 a, b, c, d, e, f, g, h = range(8) N = [ [b, c, d, e, f], # a [c, e], # b [d], # c [e], # d [f], # e [c, g, h], # f [f, h], # g [f, g] # h ] 

この表現は実際には隣接配列のセットであり、従来の隣接リストではないことを主張できます 。 Pythonのリストタイプは、実際には動的配列です。 必要に応じて、リンクリストタイプを実装し、Pythonのリストタイプの代わりに使用できます。 これにより、パフォーマンスの観点からリストへの任意の挿入が安価になりますが、おそらく同じ操作でリストの最後に新しい頂点を追加できるため、このような操作は必要ないでしょう。 組み込みリストを使用する利点は、 リストが非常に高速でよくデバッグされていることです（純粋なPythonで実装できるリスト構造とは異なります）。

グラフで作業するとき、最良のアイデアはグラフで何をする必要があるかに正確に依存するというアイデアが常に現れます。 たとえば、隣接リスト（または配列）を使用すると、オーバーヘッドを小さく保ち、任意の頂点vに対してN（v）の効率的なトラバーサルを提供できます。 ただし、 uとvが隣接しているかどうかを確認するには、 Θ（N（v））の時間がかかります。これは、高いグラフ密度（つまり、多数のエッジ）で問題になることがあります。 これらの場合、多くの隣接関係が助けになります。

ヒント：
Pythonのリストの中央からオブジェクトを削除することは、非常にコストがかかることが知られています。 終わりからの削除は一定の時間で発生します。 頂点の順序を気にしない場合は、隣接リストの末尾にある頂点で上書きしてからpopメソッドを呼び出すことにより、一定の時間でランダムな頂点を削除できます。

このビューのトピックの小さなバリエーションは、隣接する頂点のソートされたリストです。 リストが頻繁に変更されない場合は、ソートを維持し、バイセクションを使用して頂点の隣接関係を確認できます。これにより、オーバーヘッドがわずかに減少します（メモリ使用量と反復時間）。ただし、チェックの複雑さはΘ（log ₂ k）に増加しますこの頂点に隣接します。 （これはまだ非常に小さな値です。ただし、実際には、組み込みのセット型を使用することはそれほど面倒ではありません）。

別のマイナーな調整は、セットまたはリストの代わりに辞書を使用することです。 隣接する頂点は辞書キーにすることができ、追加のデータ（エッジの重みなど）を値として使用できます。 これがどのように見えるかは、以下のリストで確認できます（重みはランダムに選択されます）。

 a, b, c, d, e, f, g, h = range(8) N = [ {b:2, c:1, d:3, e:9, f:4}, # a {c:4, e:3}, # b {d:8}, # c {e:7}, # d {f:5}, # e {c:2, g:2, h:2}, # f {f:1, h:6}, # g {f:9, g:8} # h ] 

隣接辞書は、重みに関する追加情報を考慮して、他の表現と同じ方法で使用できます。

 >>> b in N[a] #  True >>> len(N[f]) #  3 >>> N[a][b] #  (a, b) 2 

必要に応じて、エッジの重み（データの代わりにNoneまたは別の値を使用）などの有用なデータがない場合でも、隣接辞書を使用できます。 これにより、隣接セットのすべての利点が得られますが、 セットをサポートしていない（非常に）古いバージョンのPython（セットはPython 2.3でセットモジュールとして導入されました。組み込みセットタイプはPython 2.4以降で使用可能）で動作します。

これまで、隣接構造（リスト、セット、または辞書）を格納するエンティティは、頂点番号でインデックス付けされたリストでした。 より柔軟なオプション（任意のハッシュされた頂点名の使用を許可）は、辞書に基づいて構築されます（隣接リストを持つ辞書は、 www.python.orgで入手可能な記事「Python Patterns-Implementing Graphs」でGuido van Rossumによって使用されました） /doc/essays/graphs.html ）。 以下のリストは、隣接セットを含む辞書の例を示しています。 その中の頂点は記号で示されていることに注意してください。

 N = { 'a': set('bcdef'), 'b': set('ce'), 'c': set('d'), 'd': set('e'), 'e': set('f'), 'f': set('cgh'), 'g': set('fh'), 'h': set('fg') } 

セットコンストラクターが上記のリストから削除されると、文字の隣接リスト（不変）として機能する隣接ストリングが残ります（わずかにオーバーヘッドが少なくなります）。 これは最良のアイデアとはほど遠いように思えますが、前述のように、すべてはプログラムに依存します。 グラフのデータはどこから取得しますか？ （たぶん、それらはすでにテキストの形になっていますか？）どのように使用しますか？

隣接行列

グラフ表現の別の一般的な形式は、隣接行列です。 主な違いは次のとおりです。各頂点のすべての隣接する頂点をリストする代わりに、値の1行（配列）を書き留めます。各行は、隣接する可能性のある頂点に対応し（グラフの各頂点にそのような頂点が少なくとも1つあります）、値を保存します（ True形式またはFalse ）頂点が実際に隣接しているかどうかを示します。 繰り返しますが、最も単純な実装は、以下のリストからわかるように、ネストされたリストを使用して取得できます。 これには、頂点に0からV-1までの番号を付ける必要があることに注意してください。 真理値は、マトリックスを読み取り可能にするために1と0（ TrueおよびFalseの代わりに）です。

 a, b, c, d, e, f, g, h = range(8) # abcdefgh N = [[0,1,1,1,1,1,0,0], # a [0,0,1,0,1,0,0,0], # b [0,0,0,1,0,0,0,0], # c [0,0,0,0,1,0,0,0], # d [0,0,0,0,0,1,0,0], # e [0,0,1,0,0,0,1,1], # f [0,0,0,0,0,1,0,1], # g [0,0,0,0,0,1,1,0]] # h 

隣接行列の使用方法は、リストおよび隣接セットとは少し異なります。 bが N [a]にあるかどうかをチェックする代わりに、マトリックスN [a] [b]のセル値が真であるかどうかをチェックします。 さらに、すべての行が同じ長さであるため、隣接する頂点の数を取得するためにlen（N [a]）を使用できなくなりました。 代わりに、 sum関数を使用できます。

 >>> N[a][b] 1 >>> sum(N[f]) 3 

隣接行列には、知っておくべきいくつかの便利なプロパティがあります。 まず、ループのあるグラフを考慮しないため（つまり、疑似グラフを使用しない）、対角線上のすべての値はfalseです。 また、無向グラフは通常、両方向のエッジのペアで記述されます。 これは、無向グラフの隣接行列が対称になることを意味します。

隣接行列を拡張して重みを使用するのは簡単です。論理値を保存する代わりに、重みを保存します。 エッジ（u、v）の場合、 N [u] [v]はTrueではなくエッジw（u、v）の重みになります 。 多くの場合、実際的な目的のために、存在しないリブには無限の重みが割り当てられます。 （これにより、既存のエッジに沿ったパスを探しているため、たとえば最短パスに含まれないようになります）。 無限を想像する方法は必ずしも明らかではありませんが、確かにいくつかの異なるオプションがあります。

それらの1つは、すべての重みが非負であることがわかっている場合に、 Noneや-1など、重みに不適切な値を使用することです。 場合によっては、本当に大きな数値を使用すると便利です。 整数の重みの場合、 sys.maxintを使用できますが、この値は必ずしも最大ではありません（長い整数の方が大きい場合があります）。 無限を反映するために導入された値： infもあります。 Pythonでは名前で直接利用できず、 float（ 'inf'）として表されます（ Python 2.6以降で動作することが保証されています。以前のバージョンでは、そのような特別な値はプラットフォーム固有でしたが、 float（ 'inf'）またはfloat（ ' Inf '）はほとんどのプラットフォームで動作するはずです）。

以下のリストは、ネストされたリストによって実装される重みマトリックスがどのように見えるかを示しています。 上記のリストと同じ重みが使用されます。

 a, b, c, d, e, f, g, h = range(8) _ = float('inf') # abcdefgh W = [[0,2,1,3,9,4,_,_], # a [_,0,4,_,3,_,_,_], # b [_,_,0,8,_,_,_,_], # c [_,_,_,0,7,_,_,_], # d [_,_,_,_,0,5,_,_], # e [_,_,2,_,_,0,2,2], # f [_,_,_,_,_,1,0,6], # g [_,_,_,_,_,9,8,0]] # h 

無限の値は短く、視覚的に区別できるため、アンダースコア（ _ ）として示されます。 当然、任意の名前を使用できます。 対角線の値はまだゼロであることに注意してください。ループがなくても、重みはしばしば距離として解釈され、頂点からそれ自体までの距離はゼロです。

もちろん、ウェイトマトリックスを使用すると、エッジのウェイトを非常に簡単に取得できますが、たとえば、頂点の隣接度のテストと決定、または隣接するすべての頂点の移動は異なる方法で行われます。 ここでは、このような無限の値を使用する必要があります（明確にするために、 inf = float（ 'inf'）を定義します）：

 >>> W[a][b] < inf #  True >>> W[c][e] < inf #  False >>> sum(1 for w in W[a] if w < inf) - 1 #  5 

対角線上の値はカウントしないため、取得した次数から1が減算されることに注意してください。 ここで次数を計算する複雑さはΘ（n）ですが、別の表現では、頂点の隣接と次数の両方を一定の時間で決定できます。 したがって、グラフの使用方法を常に正確に理解し 、適切な表現を選択する必要があります。

NumPyからの特別な配列

  NumPy   ,    .        ,    NumPy  , ,      .           n ,  : >>> N = [[0]*10 for i in range(10)]  NumPy    zeros: >>> import numpy as np >>> N = np.zeros([10,10])     ,  : A[u,v].      ,   : A[u].  NumPy     http://numpy.scipy.org.  ,      NumPy,       Python.    NumPy     Python,   ,           .         (,     Subversion): svn co http://svn.scipy.org/svn/numpy/trunk numpy    ,     NumPy,      ,     . 

ツリーの実装

当然、ツリーは特別な種類のグラフであるため、グラフの任意の表現を使用してツリーを表すことができます。 ただし、ツリーはアルゴリズムで大きな役割を果たしており、多くの適切な構造と方法が開発されています。 ほとんどのツリーベースのアルゴリズム（ツリー検索など）はグラフ理論の観点から考えることができますが、特別なデータ構造により実装が容易になります。
ルートからツリーの表現を記述する最も簡単な方法は、rib骨がルートから下がることです。 このようなツリーは、多くの場合、階層データの分岐を表示します。ルートにはすべてのオブジェクト（リーフに保存される）が表示され、各内部ノードには、このノードをルートとするツリーに含まれるオブジェクトが表示されます。 この説明は、すべての子孫サブツリーを含むリストとして各サブツリーを提示することで使用できます。 図に示されている単純なツリーを検討してください。 2。
このツリーをリストのリストとして表すことができます。

 >>> T = [["a", "b"], ["c"], ["d", ["e", "f"]]] >>> T[0][1] 'b' >>> T[2][1][0] 'e' 

各リストは基本的に、各内部ノードの子孫のリストです。 2番目の例では、ルートの3番目の子孫、次にその2番目の子孫、最後に前のノードの最初の子孫に切り替えます（このパスは図でマークされています）。


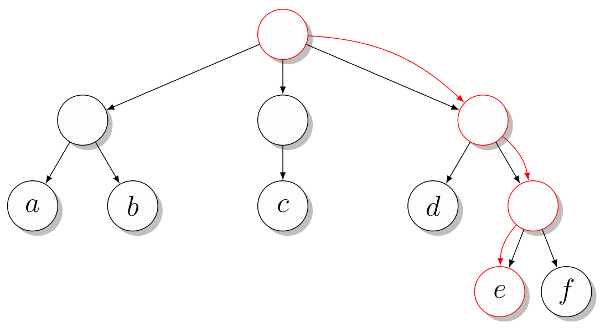
図 2.ルートからリーフへのマークされたパスを持つツリーの例

場合によっては、各ノードの子孫の最大数を事前に決定することができます。 （たとえば、 バイナリツリーの各ノードには最大2つの子を含めることができます）。 したがって、他のビュー、たとえば、下のリストのように、子孫ごとに個別の属性を持つオブジェクトを使用できます。

 class Tree: def __init__(self, left, right): self.left = left self.right = right >>> t = Tree(Tree("a", "b"), Tree("c", "d")) >>> t.right.left 'c' 

Noneを使用して、子孫が欠落していることを示すことができます（ノードに子孫が1つしかない場合）。 もちろん、さまざまな方法を組み合わせることもできます（たとえば、ノードごとにリストまたは子孫のセットを使用します）。

特に組み込みリストのサポートを持たない言語でツリーを実装する一般的な方法は、いわゆる「最初の子孫、次の兄弟」の表現です。 その中の各ノードには、バイナリツリーのように、他のノードを指す2つの「ポインター」または属性があります。 ただし、これらの属性の最初はノードの最初の子孫を指し、2番目はその次の兄弟（つまり、同じ親を持つが右側にあるノード- およそRe ）を指します。 言い換えると、ツリー内の各ノードには、その子孫のリンクリストへのポインタがあり、これらの子孫はそれぞれ独自の類似リストを参照します。 したがって、バイナリツリーを少し変更すると、以下のリストに示すマルチパスツリーが得られます。

 class Tree: def __init__(self, kids, next=None): self.kids = self.val = kids self.next = next 

ここでは、ノードへのリンクの代わりに値（たとえば、「c」）を指定するときに明確な出力を取得するために、別個のval属性が導入されています。 当然、これはすべて変更できます。 この構造を処理する方法の例を次に示します。

 >>> t = Tree(Tree("a", Tree("b", Tree("c", Tree("d"))))) >>> t.kids.next.next.val 'c' 

そして、このツリーは次のようになります。


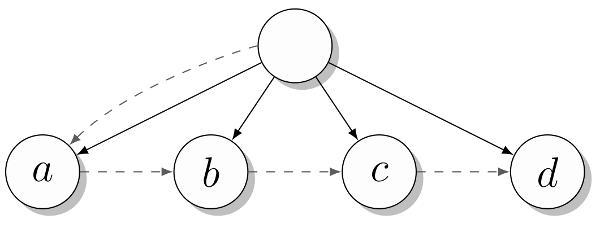子要素と次の属性は破線で示されており、ツリーの端は実線です。 私は少しだまして、行「a」、「b」などに別々のノードを表示しませんでした。 代わりに、それらをそれぞれの親ノードのラベルとして扱います。 より複雑なツリーでは、単一の属性を使用してノード値を格納し、子孫のリストを参照する代わりに、両方の目的で別個の属性が必要になる場合があります。 通常、ハードコードされたパスでここで指定されたものよりも複雑なコード（ループと再帰を含む）を使用してツリーを走査します。

デザインセットテンプレート

   (  )          ,      .       «» (     «Python Cookbook»).     ,      : class Bunch(dict): def __init__(self, *args, **kwds): super(Bunch, self).__init__(*args, **kwds) self.__dict__ = self      . -,       ,       : >>> x = Bunch(name="Jayne Cobb", position="PR") >>> x.name 'Jayne Cobb' -,   dict    ,      ()     .  : >>> T = Bunch >>> t = T(left=T(left="a", right="b"), right=T(left="c")) >>> t.left {'right': 'b', 'left': 'a'} >>> t.left.right 'b' >>> t['left']['right'] 'b' >>> "left" in t.right True >>> "right" in t.right False           .     ,    ,      . 

多くの異なるビュー

グラフには多くの表現があるという事実にもかかわらず、それらのほとんどは、この章ですでに説明した2つのタイプ（変更あり）のみを研究して使用します。 Jeremy Spinredは著書「Effective Graph Representation」で、グラフのコンピューター表現の研究者として、ほとんどの入門記事で「特にイライラする」と書いています。 よく知られている表現（リストと隣接行列）の説明は通常適切ですが、より一般的な説明はしばしば誤りです。 , :
« : . , , , , , » (. 9).

, . -, , . , ( ), ( -), , , ( ). , ( ) ( ). , , - .

-, : , , , , .

, , , , . , , , . , (u, v) Θ(1) , v — Θ(n) , Θ(d(v)) , .. .

アルゴリズムの漸近的な複雑さが表現のタイプに依存しない場合、この章で前述した経験的なテストを実行できます。または、よくあることですが、コードで最適に機能し、保守しやすいものを選択できます。
まだ触れられていないグラフを使用する重要な方法は、プレゼンテーションに関係ありません。実際、多くの問題でデータはすでにグラフまたはツリーの構造を持っているため、特別な表現を作成することなく、グラフとツリーに対応するアルゴリズムを使用できます。場合によっては、グラフ表現がプログラムの外部でコンパイルされている場合に発生します。たとえば、XMLドキュメントを解析したり、ファイルシステムディレクトリを走査したりするとき、ツリー構造はすでに作成されており、特定のAPIがあります。つまり、グラフを暗黙的に設定します。たとえば、ルービックキューブの特定の構成に対して最も効果的なソリューションを見つけるために、キューブの状態と変更方法を決定できます。ただし、各構成を明示的に説明して保存しなくても、 ( ) — . , A* , . N(v) « », , -.

, , . , , . , : , . , (.. ) . ( ), « » .

, , , . , , , . , C, . , . , :
NetworkX: http://networkx.lanl.gov
python-graph: http://code.google.com/p/python-graph
Graphine: http://gitorious.org/projects/graphine/pages/Home

, Pygr, ( http://bioinfo.mbi.ucla.edu/pygr ), Gato, ( http://gato.sourceforge.net ) PADS, ( http://www.ics.uci.edu/~eppstein/PADS ).