この記事では、コンピューターサイエンスとオートマトンの理論で非常に重要なトピック、ブール関数の最小化について説明します。 この質問は、おそらくこのトピックを勉強したか、このトピックに出会ったすべての人によって尋ねられました。
多くの方法がありますが、最も興味深いのは、形式化することができ、それに応じて多くの困難なくプログラムできる方法です。 また、任意のブール式も使用できます。 理想的な方法は発明されていません。誰もが何らかの弱点と強みを持っています。 いわゆるHypercubeメソッド-Quineメソッドに焦点を当てます。
残念ながら、この方法は完全なDNFにのみ適用できます;したがって、多数の変数では、SDNFの巨大な表現によって使用が複雑になります。
この方法は、よく知られた結合と吸収の規則を適用することにあります。
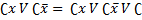

アルゴリズムを説明する前に、メソッドがハイパーキューブメソッドと呼ばれる理由を説明します。
任意の関数fを取ります。M1(f)は単位セットです。 簡単に言えば、関数が正しいステートメントになる変数のセットがたくさんあります。
ハイパーキューブは集合M1(f)です。
結合単項式は、M1(K)がM1(f)に含まれている場合に
暗黙的です。
他のK2が存在しない場合、暗黙的は単純と呼ばれ、M1(K)はM1(K2)に単純な用語で含まれます-最大のハイパーキューブに対応します。
この方法の主な段階
- 真理値表を作成します。
- M1(f)およびインプラントからのすべてのハイパーキューブを書き出します。
- 簡単なインプラントを使用してください。
- カバレッジテーブルを作成します。
- 残りの単純なインプリカントから、行き止まりのDNFを作成します。
例として、次のブール関数を取り上げます。

真理値表を作成します:
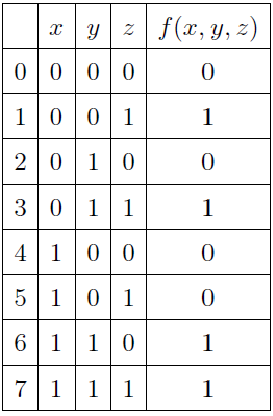
M1(f)にあるすべてのハイパーキューブと対応するインプラントを書き出します。

単純なインプラントを選択し、カバーの表を作成します。
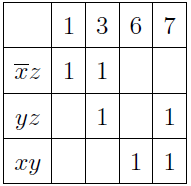
インプラントyzは他のインプラントと重複しているため、式から削除できます。 デッドエンドDNF関数の形式は次のとおりです。
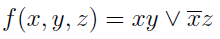
K.G.のすばらしい本を読んでみたいと思っている人なら誰でもお勧めします。 サモファロヴァ「デジタルオートマトンの応用理論」。