こんにちはコミュニティ! 最近、Habréで、文字列内の部分文字列のさまざまな検索アルゴリズムに関する優れたレビュー
記事が
掲載されました。 残念ながら、前述のアルゴリズムの詳細な説明はありませんでした。 私はこのギャップを埋めて、潜在的に思い出すことができるものを少なくともいくつか説明することにしました。 研究所からのアルゴリズムのコースをまだ覚えている人は、おそらく自分にとって新しいものを見つけることはないでしょう。
まず、「なぜこれが一体なのか」という質問を避けたいと思います。 すべてがすでに書かれています。」 はい、書かれています。 しかし、第一に、使用するツールがその制限をよりよく理解するために下位レベルでどのように機能するかを知ることは有用です。第二に、ボックスから機能するstrstr()関数が十分でない隣接領域が十分に大きいです。 第三に、運が悪く、モバイルプラットフォーム用のランタイムを開発する必要がある場合があります。それを自分で補足する場合は、購読しているものを知る方が良いでしょう(これが真空中の球状の問題ではないことを確認するには、wcslenを試してください) Android NDKのwcsstr())。
しかし、検索することは本当に不可能ですか?
事実は、すべてを「テイクアンドサーチ」として定式化する明白な方法が決して最も効果的ではないことであり、このような低レベルで比較的頻繁に呼び出される機能にとって、これは重要です。 したがって、計画は次のとおりです。
- 問題の説明:定義と規則をここにリストします。
- 「額に」の決定:ここでは、それをしない方法と理由を説明します。
- Z関数:部分文字列検索の正しい実装の最も単純なバージョン。
- Knuth-Morris-Prattアルゴリズム:別の正しい検索オプション。
- その他の検索タスク:詳細な説明なしで簡単に調べます。
問題の声明
問題の標準バージョンは次のようになります:行
A (
text )があります。 サブストリング
X (
パターン )が含まれているかどうかを確認する必要があります。ある場合は、どこから開始するかを確認します。 これは、Cでstrstr()関数が行うこととまったく同じです。これに加えて、パターンのすべての出現を検索するように依頼することもできます。 明らかに、
Xが Aより長くない場合にのみ、タスクは意味をなします
。詳細な説明を簡単にするため、一度にいくつかの概念を紹介します。
文字列とは、誰もがおそらく理解している-これは
文字列であり、空の場合もあります。
記号 、または文字は、
アルファベットと呼ばれる特定のセットに属し
ます (このアルファベットは、一般的に言えば、常識的にはアルファベットとは無関係かもしれません)。
ストリングの長さ |
A | -これは明らかにその中の文字数です。
ストリング A [ ..i
] のプレフィックスは、ストリング Aの最初のi文字のストリングです
。 ストリング A [ j ..
] のサフィックスは 、|のストリングです。
A | -j +最後の1文字。
Aの部分文字列は
A [ i..j
]として示され、
A [ i
]は文字列のi番目の文字です。 空の接尾辞や接頭辞などに関する質問 触れないでください-ローカルで対処することは難しくありません。
センチネルのようなものがまだあります-アルファベットには見られないユニークなシンボルです。 $記号で示され、そのような記号の付いた有効なアルファベットで補完されます(理論的には、実際には、入力行に表示されない記号を見つけるよりも、追加のチェックを適用する方が簡単です)。
計算では、文字列の最初の位置から文字を考慮します。 コードを書くのは伝統的にゼロから数えることで簡単です。 あるものから別のものへの移行は難しくありません。
額ソリューション
直接検索、またはよく言われる「選択して検索する」は、経験の浅いプログラマーの頭に浮かぶ最初のソリューションです。 本質は簡単です。チェックする文字列
Aに沿って進み、その中の目的の文字列
Xの最初の文字の出現を探します。 見つかったら、これが同じ望ましいエントリであるという仮説を立てます。 次に、テンプレートの後続のすべての文字を順番にチェックして、行
Aの対応する文字と一致するかどうかを確認します
。 それらがすべて一致した場合、これがまさに目の前です。 しかし、文字の1つが一致しない場合、仮説をfalseとして認識する以外に何も残りません。これにより、
Xからの最初の文字の出現に続く文字に戻ります
。多くの人々はこの時点で間違えています。戻る必要はないと信じていますが、現在の位置から行
Aの処理を続けることができます。
A =
“ AAAAB”の検索
X =
“ AAAB”の例で示すのがそれほど簡単ではない理由。 最初の仮説は、4番目の文字
A :
"AAAAB"に
つながり 、そこでミスマッチが見つかります。 ロールバックしない場合、エントリは存在しますが、見つかりません。
間違った仮説は避けられません。悪い状況下でのこのようなロールバックのため、
Aの各文字を|
X | 回。 つまり、計算の複雑さはアルゴリズムO(|
X ||
A |)の複雑さです。 したがって、段落内のフレーズの検索はドラッグアウトできます...
公平に言うと、行が小さい場合、そのようなアルゴリズムは、プロセッサの観点から予測可能な動作により、「正しい」アルゴリズムよりも速く動作することに注意する必要があります。
Z関数
文字列を検索する正しい方法のカテゴリの1つは、ある意味で2つの文字列の相関を計算することです。 まず、2行の先頭を比較するタスクは単純で簡単であることに注意してください。矛盾が見つかるか、行のいずれかが終わるまで、対応する文字を比較します。 ストリング
Aのすべての接尾部のセットを検討してください。
A | ..
] A [ |
A | -1 ..
] 、...
A [ 1 ..
] 。 行の先頭自体とその接尾辞のそれぞれを比較します。 比較は、接尾辞の最後に達するか、不一致のために一部の記号で途切れることがあります。 一致する部分の長さは、特定の接尾辞の
Z関数のコンポーネントと呼ばれます。
つまり、Z関数は、文字列の最大の共通プレフィックスとそのサフィックスの長さベクトルです。 うわー 誰かを混同したり主張したりする必要がある場合には素晴らしいフレーズですが、それが何であるかを理解するには、例を考えた方が良いでしょう。
元の文字列は
"ababcaba"です。 各接尾辞を文字列自体と比較すると、Z関数のプレートが得られます。
| 接尾辞 | ひも | | Z |
|---|
| アババカバ | アババカバ | -> | 8 |
| ババカバ | アババカバ | -> | 0 |
| アブカバ | アババカバ | -> | 2 |
| bcaba | アババカバ | -> | 0 |
| カバ | アババカバ | -> | 0 |
| あば | アババカバ | -> | 3 |
| ba | アババカバ | -> | 0 |
| a | アババカバ | -> | 1 |
接尾辞の接頭辞は部分文字列にすぎず、Z関数は先頭と中央で同時に発生する部分文字列の長さです。 Z関数のコンポーネントのすべての値を考慮すると、いくつかの規則性に気付くことができます。 まず、Z関数の値が文字列の長さを超えず、「完全な」接尾辞
A [ 1 ..
]についてのみ一致することは明らかです(したがって、この値は私たちの興味を引くものではありません。推論では省略します)。 第二に、単一のコピーの文字列に単一の文字がある場合、それはそれ自体と一致するだけであるため、文字列を2つの部分に分割し、Z関数の値は短い部分の長さを超えることはできません。
これらの観察結果の使用は、次のように提案されています。
「ababcabacab」の行で
「abca」を検索するとします。 これらの行を取り、それらの間に
センチネルを挿入して連結します:
"abca $ababcabacab" 。 このような行では、Z関数のベクトルは次のようになります。
| a b c a $ a a b a b c a b with a c a b |
| 17 0 0 1 0 2 0 4 0 0 4 0 0 1 0 2 0 |
完全なサフィックスの値を破棄する場合、センチネルの存在により、Z
iが目的のフラグメントの長さに制限されます(問題の意味では行の半分未満です)。 しかし、この最大値に達すると、部分文字列の出現位置のみで発生します。 この例では、4で目的の行の
すべての発生位置をマークし
ます (見つかったセクションは互いにオーバーラップしますが、推論はすべて同じであることに注意してください)。
つまり、Z関数のベクトルをすばやく作成し、それを使用して文字列のすべての出現箇所を検索できれば、その長さを見つけることになります。 しかし、各サフィックスのZ関数を計算する場合にのみ、これは明らかに「正面」のソリューションよりも高速ではありません。 ベクトルの次の要素の値は、前の要素に基づいて見つけることができます。
何らかの方法で、対応するi-1番目の文字までZ関数の値を計算したとします。 Z
rをすでに知っている特定の位置r <iを考えます。
したがって、この位置からのZ
r文字は、行の先頭とまったく同じです。 それらは、いわゆるZブロックを形成します。 右端のZブロック、つまり、最も遠いZブロック(最初のブロックはカウントされません)に興味があります。 場合によっては、右端のブロックの長さをゼロにすることができます(空でないブロックがi-1をカバーしない場合、Z
i-1 = 0であってもi-1stが右端になります)。
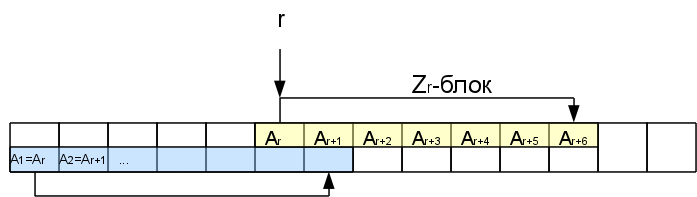
このZブロック内の後続の文字を考慮すると、このサフィックスの一部がすでに行の先頭にあるため、処理されているため、最初から次のサフィックスを比較することは意味がありません。 Zブロックの最後まで文字をすぐにスキップできます。
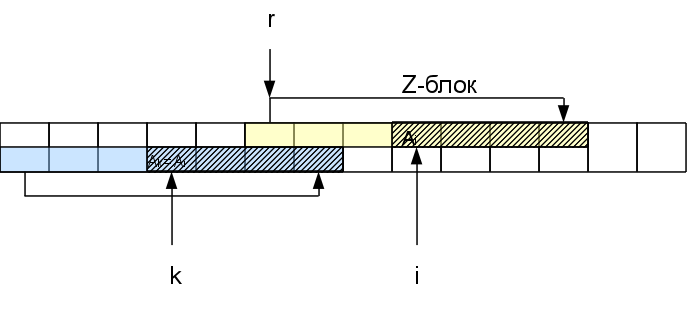
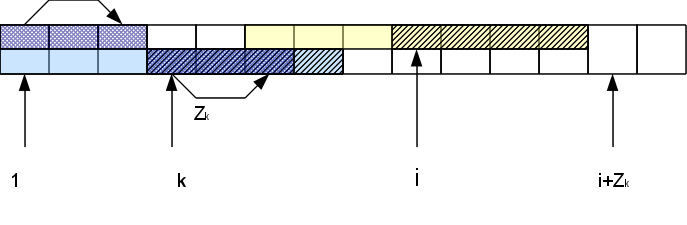
つまり、Z
rブロックにあるi番目の文字、つまり、位置k = i-r + 1の行の先頭にある対応する文字を考慮すると、 関数Z
kはすでにわかっています。 Zブロックの最後までの距離Z
r- (ir)より小さい場合、このシンボルの一致領域全体がr番目のZブロック内にあることをすぐに確認できます。つまり、結果は次のようになります。行の先頭:Z
i = Z
k Z
k > = Z
r- (ir)の場合、Z
iもZ
r- (ir)以上です。 それがどれだけあるかを知るには、Zブロックに続く文字をチェックする必要があります。 さらに、これらの文字のhが行の先頭の対応する文字と一致する場合、Z
iはhずつ増加します。Zi = Z
k + h。 その結果、新しい右端のZブロックがある場合があります(h> 0の場合)。
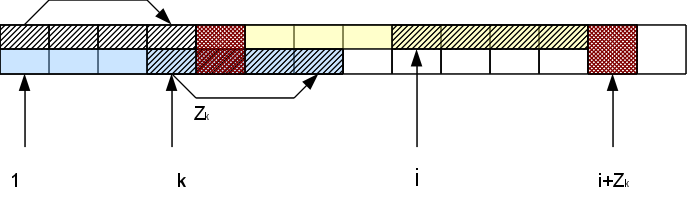
したがって、右端のZブロックの右側でシンボルを比較するだけでよく、比較が成功したため、ブロックは右側に「移動」し、失敗したブロックはこの位置の計算が終了したことを報告します。 これにより、文字列の長さに沿って線形時間でZ関数のベクトル全体を構築できます。
このアルゴリズムを適用して部分文字列を検索すると、時間の複雑さO(|
A | + |
X |)が得られます。これは、最初のバージョンの製品よりもはるかに優れています。 確かに、Z関数のベクトルを保存する必要がありました。これは、O(|
A | + |
X |)の追加メモリを必要とします。 実際、すべてのオカレンスを検索する必要はないが、1つだけで十分な場合、Zブロックの長さを||より大きくすることはできないため、O(|
X |)メモリーを省くことができます。
X |、さらに、最初の発生を検出した後、行の処理を続行できません。
最後に、Z関数を計算する関数の例。 トリックのないモデルバージョンです。
void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } }
void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } }
Knuth-Morris-Prattアルゴリズム(KMP)
前の方法の論理的な単純さにもかかわらず、別のアルゴリズムがより一般的であり、ある意味ではZ関数の逆です
-Knut-Morris-Pratt (KMP)
アルゴリズム 。
接頭辞関数の概念を紹介し
ます 。 i番目の位置の接頭辞関数は、iより短く、長さiの接頭辞の接尾辞と一致する最大行接頭辞の長さです。 Z関数の定義が対戦相手を完全に無効にしなかった場合、このコンボで間違いなくその場所に配置できます:)そして、人間の言語では次のようになります:考えられるすべての行接頭辞を取得し、接頭辞の末尾との最長開始一致を調べます(些細な偶然の一致は考慮しません)私自身と)。
「ababcaba」の例を次に示します。
| プレフィックス | プレフィックス | p |
|---|
| a | a | 0 |
| ab | ab | 0 |
| ab a | 学士 | 1 |
| ab ab | ab ab | 2 |
| ababc | ababc | 0 |
| ababc a | ババカ | 1 |
| ababc ab | アブキャブ | 2 |
| ababc aba | アバ・バカバ | 3 |
繰り返しますが、プレフィックス関数の多くのプロパティを観察します。 最初に、値は、定義から直接得られる番号によって上に制限されます-プレフィックスの長さは、プレフィックス関数よりも大きくなければなりません。 第二に、同様に一意の文字は文字列を2つの部分に分割し、プレフィックス関数の最大値を小さい方の部分の長さに制限します-長いものはすべて、他のものと等しくない一意の文字を含むためです。
これから、興味のある結論が得られます。 この理論的上限のある要素で達成したと仮定します。 これは、最初の部分が最後の部分と一致し、そのうちの1つが「完全な」半分を表す、そのようなプレフィックスがここで終了したことを意味します。 接頭辞では、半分が完全に前にある必要があることは明らかです。つまり、この仮定では短い半分になるはずですが、長い半分では最大になります。
したがって、前の部分のように、目的の行とセンチネルを調べている行を連結すると、プレフィックス関数のコンポーネント内の目的の部分文字列の長さのエントリポイントは、エントリが終了する場所に対応します。 たとえば、
「ababcabcacab」の行で
「abca」を探します。
「abca $ ababcabcacab」の連結バージョン。 プレフィックス関数は次のようになります。
| a b c a $ a a b a b c a b with a c a b |
| 0 0 0 1 0 1 2 1 2 3 4 2 3 4 0 1 2 |
繰り返しますが、部分文字列のすべての出現が一気に見つかりました-それらは4で終わります。 このプレフィックス関数を効率的に計算する方法を理解する必要があります。 アルゴリズムの考え方は、Z関数を構築する考え方とは少し異なります。

プレフィックス関数の最初の値は明らかに0です。i番目の位置までのプレフィックス関数をカウントします。 i + 1番目の文字を検討してください。 i番目の位置の接頭辞関数の値がPiの場合、接頭辞
A [ .. Pi
]は部分文字列
A [ iP
i + 1..i
]と一致します。 シンボル
A [ P
i +1
]が
A [ i + 1
]と一致する場合、P
i + 1 = P
i +1と安全に書くことができます。 しかし、そうでない場合、値はそれより小さくても同じでもかまいません。 もちろん、Pi = 0の場合、あまり減少する場所はないため、この場合はPi
+ 1 = 0です。 P
i > 0と仮定します。 次に、文字列に接頭辞
A [ ..P
i ]があります。これは、部分文字列
A [ iP
i + 1..i
]と同等です。 必要なプレフィックス機能は、これらの同等のセクションと処理される文字内で形成されます。つまり、プレフィックスの後の行全体を忘れて、このプレフィックスとi + 1番目の文字だけを残すことができます。状況は同じです。
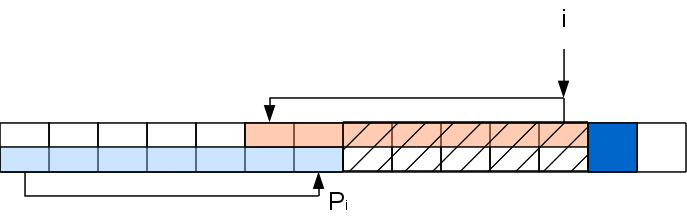
このステップでのタスクは、中間が切り取られた行の問題に縮小されました:
A [ ..P
i ] A [ i + 1
] 、これは同じ方法で再帰的に解決できます(ただし、末尾再帰はまったく再帰ではなく、ループです)。 つまり、
A [ P
P i +1
]が
A [ i + 1
]に一致する場合、P
i + 1 = P
P i +1になります。 一致するか0になるまで、この手順を繰り返します。
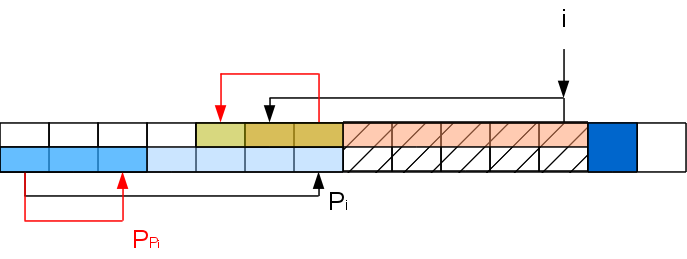
これらの操作を繰り返すと警告が表示されます。ネストされた2つのサイクルが発生しているようです。 しかし、これはそうではありません。 実際、長さkのネストされたループは、i + 1番目の位置のプレフィックス関数を少なくともk-1削減し、プレフィックス関数をそのような値に増やすには、少なくともk-1倍以上成功する必要がありますk-1文字を処理して文字を一致させます。 つまり、サイクルの長さはそのようなサイクルの実行間隔に対応するため、アルゴリズムの複雑さは処理された文字列の長さに沿って線形になります。 ここでの状況は、メモリの場合とZ関数の場合と同じです-線の長さに沿って線形ですが、保存する方法があります。 さらに、文字が順番に処理されるという便利な事実があります。つまり、最初の出現をすでに受け取っている場合、行全体を処理する必要はありません。
さて、たとえば、コードの一部:
void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } }
void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } }
アルゴリズムがより複雑であるという事実にもかかわらず、その実装はZ関数よりもさらに単純です。
その他の検索タスク
その後、文字列検索タスクはこれに限定されず、他のタスクおよび他のソリューションがあるため、興味がない場合はさらに読むことはできないという手紙がたくさんあります。 この情報は、単に慣れるためのものであり、必要に応じて、少なくとも「すべてが私たちの前に盗まれた」ことに注意し、車輪を再発明することはありません。
上記のアルゴリズムは線形実行時間を保証しますが
、ボイヤー・ムーアアルゴリズムは「デフォルト
アルゴリズム 」というタイトルを受け取りました。 平均すると、線形時間も得られますが、この線形関数のより良い定数もありますが、これは平均です。 「悪い」データがありますが、そのデータは単純な「正面」の比較よりも優れています(まあ、qsortと同じように)。 それは非常に紛らわしいので、考慮しません-とにかく、もちろん。 自然言語のテキスト処理に焦点を当て、その最適化において単語の統計的特性に依存する多くのエキゾチックなアルゴリズムがあります。
さて、O(|
X | + |
A |)の何らかの方法で文字列内の部分文字列を検索するアルゴリズムがあります。 ここで、ゲストブックエンジンを作成しているとします。 禁止されているわいせつな単語のリストがあります(これは役に立たないことは明らかですが、タスクは単なる例です)。 メッセージをフィルタリングします。 メッセージ内の禁止されている各単語を検索し、... O(|
X 1 | + |
X 2 | + ... + |
X n | + n |
A |)が必要です。 どういうわけか、特に「偉大で力強い」の「強大な表現」の辞書が非常に「強大」である場合。 この場合、検索文字列の辞書を前処理して、検索がO(|
X 1 | + |
X 2 | + ... + |
X n | + |
A |)のみを占めるようにする方法があります。メッセージが長い場合。
このような前処理は、辞書からトライを構築することになります。ツリーはダミーのルートから始まり、ノードは辞書の単語の文字に対応し、ツリーノードの深さは単語の文字の数に対応します。 辞書から単語が終わるノードはターミナルと呼ばれ、何らかの方法でマークされます(図の赤)。
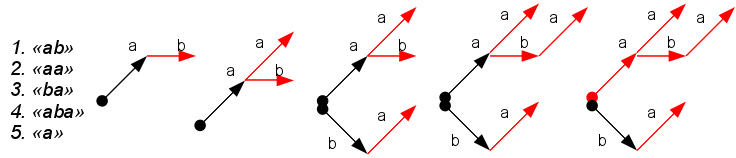
結果のツリーは、KMPアルゴリズムのプレフィックス関数に類似しています。 これを使用すると、辞書句内のすべての単語の出現箇所をすべて検索できます。 ツリーを調べて、ツリーノードの形で次の文字の存在を確認し、同時に終端の頂点をマークする必要があります-これらは単語の出現です。 ツリーに対応するノードがない場合、ILCの場合と同様に、特別なリンクを使用してツリーの上位でロールバックが発生します。 このアルゴリズムは
、Aho-Korasikアルゴリズムと呼ばれ
ます 。 同じスキームを使用して、入力時に検索し、電子辞書の次の文字を予測できます。
この例では、ボロンの作成は簡単です。ボロンに順番に単語を追加するだけです(「キックバック」用の追加リンクのみのニュアンス)。 このツリーのメモリ使用量を減らすことを目的とした最適化がいくつかあります(いわゆるボロン圧縮-分岐せずにセクションをスキップする)。 実際には、これらの最適化はほぼ必須です。 このアルゴリズムの欠点は、アルファベット順の依存性です。ノードと占有メモリの処理時間は、潜在的な子の数に依存し、これはアルファベットのサイズに等しくなります。 大きなアルファベットの場合、これは深刻な問題です(Unicode文字のセットを想像できますか?)。 このすべてについて、この
habratopikaで、またはGoogleインデックスを使用して詳細を読むことができます-この問題に関する多くの情報があります。
次に、別のタスクを見てみましょう。 前のもので、後で来るデータで何を見つける必要があるかを事前に知っていた場合、ここではまったく逆です:事前に彼らが検索する行が与えられましたが、検索するものは不明ですが、彼らは多くを検索します 典型的な例は検索エンジンです。 単語が検索されるドキュメントは事前に知られていますが、そこで検索される単語は外出先に散らばっています。 ここでも、O(|
X 1 | + |
X 2 | + ... + |
X n | + n |
A |)の代わりにO(|
X 1 | + |
X 2 | + ... + |
X n | + |
A |)?
既存の文字列のすべての可能な接尾辞が存在するホウ素を構築することが提案されています。 次に、テンプレートの検索は、目的のテンプレートに対応するツリー内のパスの存在をチェックすることになります。 すべての接尾辞を徹底的に検索してこのようなホウ素を作成する場合、この手順にはO(|
A |
2 )時間と大量のメモリが必要になります。 しかし、幸いなことに、圧縮ツリーでそのようなツリーをすぐに構築できるアルゴリズムがあります-
サフィックスツリー 、そしてO(|
A |)でそれを行います。 最近Habréでこれ
に関する記事がありまし
たので、興味のある人はそこで
Ukkonenアルゴリズムについて読むことができます。
通常、接尾辞ツリーには悪い点が2つあります。それはツリーであるということと、ツリーのノードがアルファベット順に依存しているということです。
サフィックス配列はこれらの欠点を免れ
ています。 接尾辞配列の本質は、文字列のすべての接尾辞が並べ替えられている場合、部分文字列の検索は、目的のパターンの最初の文字で隣接する接尾辞のグループを検索し、後続のものの範囲をさらに絞り込むことになります。 同時に、サフィックス自体をソートされた形式で保存する必要はありません;ソースデータでサフィックスが始まる位置を保存するだけで十分です。 確かに、この構造の時間依存性はわずかに悪くなります。1回の検索では、考えてすべてを慎重に行うとO(|
X | + log |
A |)かかり、気にしない場合はO(|
X | log |
A |)です。 比較のために、固定アルファベットO(|
X |)のツリーで。 ただし、これがツリーではなく配列であるという事実は、メモリキャッシングの状況を改善し、プロセッサ遷移予測のタスクを容易にします。 サフィックス配列は、Kärkkäinen-Sandersアルゴリズムを使用して線形時間で構築されます(すみませんが、ロシア語でどのように聞こえるかはほとんどわかりません)。 今日、これは最も人気のある行のインデックス付け方法の1つです。
ここでは、近似文字列検索と類似度の分析の質問には触れません。これは、この記事に詰め込むには広すぎる領域です。 私はただ人々がそこでパンを何もせずに食べず、多くの異なるアプローチを考え出したので、あなたが同様の問題に遭遇したら、見つけて読んでください。 おそらく、この問題はすでに解決されています。
読んでくれた人に感謝します! そして、これを読んだ人に、どうもありがとう!
UPD:ホウ素に関する重要な記事への
リンクを追加しました(レイであり、プレフィックスツリーであり、ロードされたツリーであり、トライです)。