液体窒素を装備したオーバークロッカーは、最新のチップが公称周波数よりも数倍高い周波数で安定して動作し、それに対応して性能が向上することを繰り返し示しています。 それにもかかわらず、「ギガヘルツレース」の分野での進歩はずっと前に確実に止まりました。 3 GHz以上の周波数を持つ最初の「Pentium 4」は、ほぼ10年前の2002年に登場しました。 過去数年にわたり、技術プロセスの標準は180 nmから32 nmに低下しましたが、それでも標準動作周波数を大幅に上げることはありませんでした。 すべては、デジタルロジックの要素の巨大な熱放射にかかっています。

「熱放出の問題」は、情報エントロピーと熱力学エントロピーの深い関係、および閉じたシステムの全エントロピーの減少を禁止する熱力学の第二法則に基づいています。 情報エントロピーを削減する計算は、熱力学的エントロピーの増加、つまり熱の発生につながる必要があります。 1961年のロルフ・ランダウアーは[ pdf ]、1ビットの情報の破壊が少なくともk∙T∙2ジュールのエネルギーの放出につながることを示しました。ここで、kはボルツマン定数、Tはシステムの温度です。 このエネルギー自体は小さいです。T= 300Kの場合、ビットあたりわずか0.017 eVですが、プロセッサ全体で見ると、総エネルギーは動作の1秒ごとに約1ジュール、つまり約1ワットに上昇します[ Computerra No. 538 ] 。 実際には、この理論上の最小値に、実際の半導体の非ゼロ抵抗およびその他の非理想性が掛けられます。 その結果、私たちは熱の面で鉄よりも優れたプロセッサーを手に入れました。


最新のプロセッサでの情報の破壊は、最新のデジタル回路の「レンガ」である「NAND」ゲートで、常に最下位レベルで発生します。 入力として2ビットを使用すると、バルブは1ビットのみのサイズの結果を生成します。当然、元の引数の値を復元することはできません。 より厳密には、AND-NOTゲートによる各計算により、情報エントロピーが1.189ビット削減され、それに応じて、少なくとも〜0.02 eVの熱が放散されます。 今日人気のないOR-NOTでも、状況は似ています。

メモリセルでは、以前の値の破壊につながるエントリはすべて改善されます。 プログラマーにとって、古いデータは単純に「失われ」ますが、電荷とエネルギーの保存の法則では、物理的なレベルで「そのように」失われることはできません。 実際、古い情報は破壊されず、熱とスプリアス放射の形で空間に散らばっています。

30年以上にわたり、情報を破壊することなく計算を整理する方法が知られており、これはランダウアーの原理に該当せず、理論的にエネルギー効率の高いプロセッサを作成できます。 この方法は、保守的または「保存」ロジックと呼ばれます。 残念ながら、シリコンでコンパクトな物理的実装を作成することはできませんでした。インダクタの小型化が不十分なMOSトランジスタでの実装方法のみが知られています。 一方、このアプローチは、光学式コンピューター（ベニオフのモデルなど）を含むほとんどのタイプの量子コンピューターにとって自然です

長年にわたって、保守的なロジックは「ハードウェアで」実装することなく有用な数学的抽象化であることが判明しました。ブロックセルオートマトンはその基礎に基づいて作成され、「限られたリソースの」問題を解決するときに非常に便利です。 この数学の分野は現在非常に活発に開発されており、おそらく10年ほどで、ブロックセルオートマトンはプログラマーの間で通常のものよりもさらに有名になるでしょう。

この記事の登場につながった「蝶の羽ばたき」は、同志プラホフによって提起された質問「ロシア語はどうですか？」、ヤンデックスでさえ知らない答えです。 上記の2004年のComputerraの記事に加えて、ロシアの保守的な論理に関する情報はまったくありません-理論的な基礎は、ちょうど50年前の1961年にソビエトの物理学者LandauとLifshitsによって築かれたため、さらに攻撃的です。 「ギャグをスマックする」のではなく、少なくともわずかにこのギャップを排除するために、ジャーナルTheoretical Physics No. 1982年の21。 （フレドキン、エドワードおよびトフォリ、トマソ、「保守的論理」、Int。J. Theor。Phys。21（1982）、219–253; pdf ）。 この記事では、保守的なロジックに基づいたシステムの物理、ロジック、および回路に関するすべての主要なポイントを明らかにします。

保守的な論理

保存的または保存ロジックは、2つの基本的な物理的原則に基づく計算の組織化の数学モデルです。プロセスの可逆性と保存則です。

1.物理的な基礎

（抽象的なセクションの番号付けは、記事の各部の番号付けと一致しません- およそPer ）

計算は、それがどのように実行されても、人または機械によって、特定の物理法則に従う必要があります。 特に、情報の伝播速度は光の速度によって制限され、最終システムの情報量も有限でなければなりません。 より複雑な制限があります。

すべての物理法則は、動的と統計に分類できます。 前者は、完全に定義された顕微鏡システムで個々のオブジェクトの動作を記述し、古典的な力学では、実験の結果を正確に予測することを可能にします。 オブジェクトが多すぎてそれぞれをカウントできない場合、マクロシステム内の同種のオブジェクトの平均的な動作を記述する統計法則が適用されます。 これらを使用すると、全体像を評価できますが、特定のオブジェクトの動作を予測する機会は提供されません。

ミクロレベルでは、私たちの世界にはさまざまな基本的な同質性と対称性があり、その多くはマクロレベルでの「保存法」の出現につながります。 したがって、時間の均一性は、エネルギー保存の法則、空間の均一性-運動量の保存の法則、および空間の等方性（方向の対称性）の実現を保証し、回転モーメントの保存につながります。

動的な基本物理法則はすべて、座標を逆座標に置き換えるという意味で可逆です。 すべてのボールを厳密に反対方向に移動させると、ビリヤードのビートを逆にすることができます。 一方、統計的物理法則は熱力学の原則に従い、時間の矢印を逆にしないと可逆的ではありません。壊れた花瓶は破片から組み立てられません。 特に、マクロレベルで動作する従来の計算モデルは、AND-NOTまたはOR-NOTゲートに基づいています。 このようなモデルでの計算には、Landauerの原則に従ったエネルギーコストが必要です。

計算のあらゆる組織において、デジタル情報は、システムの番号付き安定状態を物理的に表します。

ご注意 あたり ：この記事は物理学者を対象としているため、著者は物理学者に明らかなことを説明するものではありません。 最後の文はこれについてです：たとえば、メモリセルのコンデンサは、「充電済み」または「放電済み」の2つの論理状態になります（もちろん、コンデンサの「物理的」充電は実際には連続的ですが、ブールではありません）。 これらの論理状態の安定性は、充電されたコンデンサを再充電し、放電されたコンデンサを放電する特別な電子再生回路によって保証されます。 この場合、「充電済み」状態と「放電済み」状態のエネルギーの差は、熱ノイズのレベルに比べて大きいはずです。

実際、これらの状態は電気的、光学的などになりますが、以下ではそれらを「機械的」と呼び、熱力学的状態と区別します。 熱力学的状態は、物質を構成する個々の原子および分子の自由度です。 物質の1グラムには、そのような自由度の数である約10 ²³ （アボガドロ数）という巨大なものがあり、それらは統計的な方法と法則によってのみ考慮することができます。

熱力学の第二法則は、閉じたシステムの総エントロピーが減少することはできないと言っています。 Landauerの原理は、情報エントロピーと熱力学的エントロピーの間のエネルギー関係を確立します。 多くのアルゴリズムは情報エントロピーの減少をもたらしますが、そのような減少は熱力学的エントロピー（発熱）の増加によって補償されるか、禁止されるべきです。

したがって、計算の物理的編成に対する2つの根本的に異なるアプローチが可能です。

情報を保存するための「保守的」または「保存的」アプローチでは、熱力学的状態とエントロピーの交換が不可能な機械的条件が選択されます。 このようなシステムでは、情報エントロピーを低下させる操作、特に情報破壊操作を禁止する必要があります。 したがって、すべての操作は可逆的でなければなりません。 LandauとLivshitsは、そのようなシステムでは、例えば保存則によって「保護された」電荷やモーメントなど、不変の追加量が存在する必要があることを示しました。その場合にのみ、「電荷」から「温度」への遷移は不可能になります。 クローズドシステムで利用可能なこれらの量の合計レベルは一定値であり、システムで発生するプロセスに依存しません。

保守的なものとは異なり、通常の「フォンノイマン的」アプローチでは、計算は最初は不可逆的です。 熱力学の第2法則を満たすためには、機械的自由度と熱力学的な自由度の間でエントロピーとエネルギーを交換するためのパスが存在する必要があります。 このような経路は、熱的変動が機械的状態で保存された情報を破壊できないように、片側（つまり、不可逆的）でなければなりません。 しかし、ミクロレベルではすべてのプロセスが可逆的であるため、機械的状態間のエネルギー差が熱力学的状態間のエネルギー差よりもはるかに大きい場合にのみ、エントロピーの片側フローを実現することができます。 現代のコンピューター技術では（1982- 約Per。 ）違いは8〜12桁です。

ご注意 あたり ：私たちのシステムは、非常に小さなW字型のガラスとその中のボールで構成されていると想像してください。 ボールには2つの安定した位置があります-ガラスの左半分と右半分の下部です。 これらは、番号を付けて情報を保存できる機械的な状態です。 新しい情報をグラスに「書き込む」ためには、ボールの位置を変えるという意味で、グラスの中央の丘にボールを上げ、この上昇に一定のエネルギーを費やす必要があります。 次に、すでにガラスの反対側で、この余分なエネルギーを取り戻すか、何らかの方法で消す必要があります。そうしないと、ボールは平衡位置の周りで大きな振幅で振動します。 過剰エネルギーの選択プロセスがどのように組織化されても、その一部はとにかく熱に変わりますが、「丘の高さ」が小さいほど、エネルギー損失は少なくなります。

実際のシステムでは、ボールとガラスの両方で一定の熱変動が発生することを想像してください。 このような振動の強さは温度に比例します。 温度が低い間、ボールは常に完全に平衡点にあるとは限りませんが、少なくとも頻繁に平衡点に戻ります。 しかし、温度が上昇すると、振動が激しくなり、ある時点でボールが丘を自然に「ジャンプ」する機会を得ます。 いかなる場合でもこれを許可するべきではないため、「スライド」は非常に高くなければならず、通常の克服には必然的にエネルギーコストが高くなります。

今日のコンピューティングテクノロジーはすべて、第2の「不可逆的な」パス上に構築されています。 不可逆性は、基本的な論理回路、トランジスタのpn接合に特別に定められており、計算された高レベルアルゴリズムが正式に可逆的であっても、最新のプロセッサで実行すると、個々のステップの少なくとも一部は最低レベルで不可逆的です。 不可逆性はまた、大きな発熱を意味し、達成可能な性能を制限します。

2.保守的なロジックの基本要素

保守的な原理に基づく計算モデルでは、特定の条件を満たす基本的な論理要素を使用する必要があります。 特に、それらは可逆的であり、まさに加算的な量（電荷、モーメント）を保持する必要があります。 2番目の要件から、要素の入力の数は出力の数と等しくなければならないことになります。つまり、厳密に「1対1」の機能構成を意味します。

ご注意 あたり ：従来の回路では、1つの論理要素の出力を他のいくつかの要素の入力に接続できます（「分岐」）。 保守的な回路では、1つの出力は厳密に次の要素の1つの入力に行く必要があります。 分岐には特別な論理要素が必要です（以下を参照）。

保守的なロジックは、リピーターとフレドキンゲートという2つの要素に基づいています。

リピーター （ユニットワイヤ、文字通り「エレメンタリーコンダクター」）は、1クロックサイクルの遅延で、入力に供給される出力信号を単純に繰り返します。 回路のクロック周波数を決定するのは、リピーターの速度です。 正式には、リピーター関数は次のように表されます。
y ^t = x ^t-1

凡例：



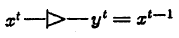
リピーターは、ストレージ（自身に閉じられている）と回路内の情報転送の両方の機能を実行できますが、その主なタスクは、信号をクロックジェネレーターと同期させることです。

リピーターの反対側の要素は同じリピーターですが、反対方向に向けられています。

特定のクロックサイクルでのリピータの出力の値は、保守的なロジックのデジタル回路の内部状態を完全に表します。つまり、リピータの出力はそのような回路の状態変数です。 リピーターの出力での値の合計は、同じ加算値（「合計料金」）であり、クローズドシステムの場合は一定値です。 回路内のリピーターの総数は、この回路の自由度の数と見なすことができます。

リピータは、従来の「フォンノイマン」回路の遅延要素とほとんど同じですが、同等ではありません。

Fredkinゲートは、3つの入力u、x1、x2と3つの出力v、y1、y2を備えたデバイスで、2つのデータラインの制御された「オーバーラップ」（「クロス」）の機能を実装します（図を参照）。 出力vは常に入力uと一致します。 u = 1の場合、出力y1、y2は入力x1、x2と等しくなります。 u = 0、y1 = x2およびy2 = x1の場合（表を参照）

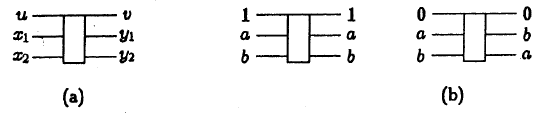
フレドキンバルブの真理値表：
（u、x1、x2）=>（v、y1、y2）
0,0,0 => 0,0,0
0,0,1 => 0,1,0
0,1,0 => 0,0,1
0,1,1 => 0,1,1
1,0,0 => 1,0,0
1,0,1 => 1,0,1
1,1,0 => 1,1,0
1,1,1 => 1,1,1

フレッドキンの弁はそれ自体に逆になっています。

したがって、保守的なロジックの回路は制御可能な条件付き信号ルーターであり、その出力では、前のクロックサイクルでの入力値の特定の制御可能な再配置が形成されます。

3.保守的な回路

保守的なロジックでは、チューリングマシン（Bennett、1973）とユニバーサルセルオートマトン（Toffoli、1980）を実装できます。 したがって、保守的な論理により、教会の計算可能な問題を解決することができます。

保守的なロジックで任意の関数を実装するプロセスは、従来のロジックでの同じプロセスと非常に似ています。

従来の回路のように、いくつかの機能を実装する場合、定数が使用されます-定数値0または1のソース。一方、計算の結果として、必要な結果が得られるだけでなく、特定のアルゴリズムでさらに使用する必要のない副次的な結果も得られます。 副作用は「ゴミ」または「シンク」と呼ばれます。 保守的な論理では、信号は「どこからでも」現れず、「どこでも」消えないため、「余分な」結果の行を破棄することは単に不可能であり、特別な方法で廃棄する必要があります（空間に散らばっている）。

図は、特定の関数φの計算単位の記号を示しています。



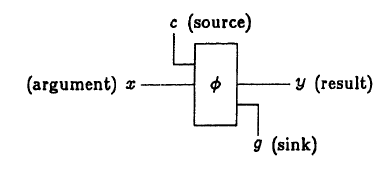
これは、ブロック " I "の配置方法です。


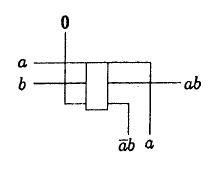
（シンクの1つは引数のコピーであることに注意してください）

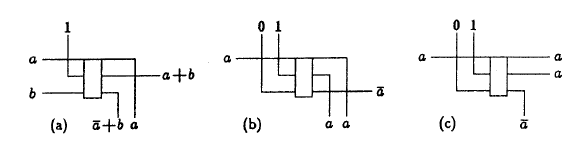
次の図は、論理関数「 OR 」（a）、「 NOT 」（b）、および信号スプリッター 2a-aの実装を示しています。 最後の2つは、結論の論理的な役割のみが異なります。



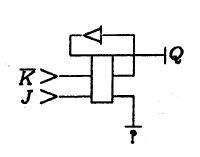
次の図は、単純なメモリ要素であるJKトリガーを示しています。 疑問符は、意味のないドレインを示します。



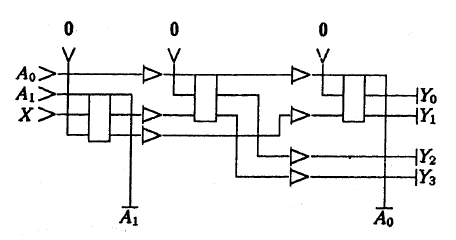
より複雑なスキームは次のとおりです。X信号をバイナリアドレスA0、A1に送信し、4つの出力Y0〜Y3のいずれかに送信するデマルチプレクサ ：



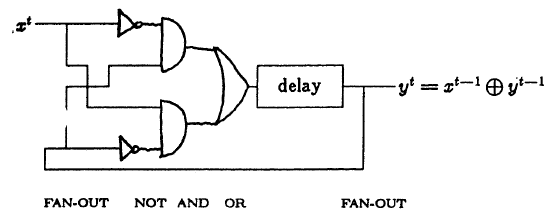
保守的なロジックでは、「通常の」ロジックの任意の回路を実装できます。 たとえば、次の3つの図は、 シングルビットシーケンシャル加算器の実装を示しています。1つ目は従来のロジック（古い表記）、2つ目と3つ目は保守的なロジックです。 さらに、2番目のスキームは、最初のスキームを単に置換することで組み立てられ、3番目のスキームは「ゼロから」作成されます。 リピーターと遅延要素の違いは、回路上で確認できます。保守的な回路では、信号は明示的に同期されます。

4.排水の問題

保守的なロジックの実用的な価値は、たとえば量子コンピューターに実装される場合、実際の計算での利用を必要とするドレインの数に完全に依存します。 ドレインの破壊は、従来の回路に固有の「エネルギー生成」動作です。 プロセッサのトリガーごとに独自のドレインがある場合、エネルギー解放のゲインはありません。

排水溝の出現を完全に回避することは不可能です。 たとえば、多くの実際のアルゴリズムでは、最終結果は任意の数値の合計です。 しかし、加算演算自体は不可逆的です。なぜなら、その結果のみを知っているため、初期項を決定することは不可能だからです。 さまざまなプログラムやアルゴリズムを順番に実行するユニバーサルプロセッサでは、単純に蓄積するには「余分な」情報が多すぎます。 特別な「エントロピー交換器」が必要になり、そこに廃棄物の結果が配信されます。

計算される関数のタイプに応じて、必要な定数とシンクの数の比率について考えられる3つのシナリオがあります（図を参照）。



3番目の最良のシナリオは、計算された関数f自体が可逆的であり、現在の保存則に従う場合にのみ可能です。

ドレインの問題を部分的に解決すると同時に、反転回路を使用して定数の生成を順序付ける方法があります。 「反転」とは、特定の回路を反転する、つまり特定の出力とドレインから入力と定数を復元する回路を意味します。 保守的なロジックのすべての回路は可逆であるため、回路を反転するには、単にすべてのリピータを反対方向に回し、入力を出力と呼ぶだけで十分です。 または、同じことですが、ミラーにスキームを反映します（図を参照）。



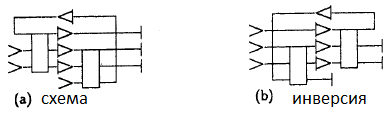
直接回路と反転回路は、互いに直列に接続できます。 この方法で取得された要素は、定数を必要とせずにドレインを作成することなく、大きな遅延で入力を複製しますが、内部のどこかに元の関数の計算結果があります（図を参照）。



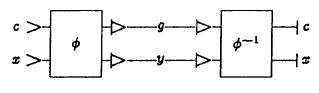
元の関数の計算値は、スキーム「スパイスプリッター」に「埋め込まれている」場合、「取得」できます。



それでも、このようなスキームを使用するには、定数（より正確には、必要なゼロと1を1回入力する必要がある「スクラッチパッド」レジスタ）を提供するとともに、出力レジスタと出力レジスタの両方を正しく入力する必要があります。 このようなスキームの出力は、a）引数のコピー、b）結果、およびc）結果の反転であり、これのいずれかが他のどこでも使用されていない場合、それらも破棄する必要があります。

この方法の主な利点は、「ドレイン」ラインの数が入力のビット深度のみに比例することです。 同時に、ロジックのほとんどの実際の機能を実装するために必要なゲートの数は、入力ビット深度の指数としてほぼ増加します。 従来の回路では、すべてのバルブが保守的に熱を放出します。つまり、「ドレイン」のみであるため、入力のビット深度が大きくなると、メリットは大きくなります。

5.ビリヤードボールのモデル

このパートでは、保守的なロジックが実装された抽象的な物理モデルを示します。

モデルは、ビリヤードボールが厳密に指定された方向に摩擦なしで移動する平面です。 ボールの速度、許容方向、およびサイズは、メジャーに対応する個別の瞬間に、ボールが45 '回転した長方形のグリッドを形成する小さな点のセットにのみ存在するように選択されます（図を参照）。 ボールが隣接するポイントに落ちると、それらの間で弾性衝突が発生します。



論理単位はボールの存在であり、ゼロ-その不在です。

2つのボールの軌道が交差する場合、任意のグリッドポイントを「相互作用ゲート」と宣言できます。 これらのボールの出口の方向は、両方の存在に依存します。



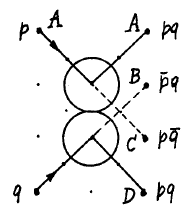
平面には、固定壁またはミラーを設置できます。 ミラーを使用すると、ボールの経路（d）を回転（a）、シフト（b）、保持、安全に横断できます（d）。 最後の要素（d）は「重要なクロスオーバー」と呼ばれ、ボールが「互いに通過」できるようにします。



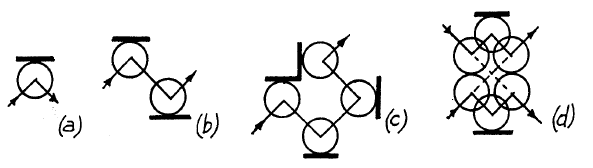
管理されたスイッチを作成することが可能です。 この図は、単純なスイッチのブロック図、逆スイッチ要素の指定、および単純なスイッチの実装図を示しています。




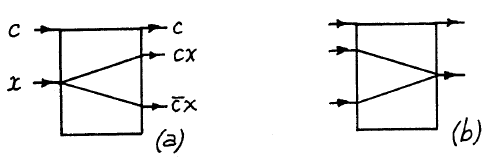
最後に、単純なスイッチと非自明なクロスオーバー（「ブリッジ」で示される）から、Fredkinバルブを構築できます（明確にするために、回転ミラーと遅延は示されていません）。



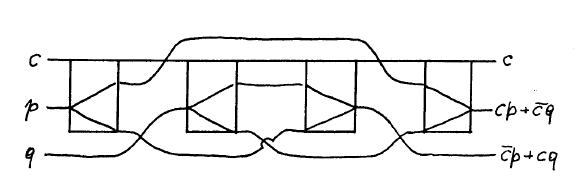
実際の物理的な実施形態に関しては、ガスの分子は実際のビリヤードボールよりもボールの役割により適していますが、どちらのオプションも実装されていません。
ビリヤードボールモデルの主な利点は、その単純さです：特別に選択された角度と速度のおかげで、すべての衝突の結果は、浮動小数点数、高価な丸め操作などを伴わずに、単純なブール関数によって計算できます。 これにより、従来のコンピューター上で非常に大規模な保守的なロジックのスキームでさえも迅速にシミュレートできます。

6.保守的なロジックに関する「複雑な」質問

1.保守的なロジックで任意の計算が可能ですか？ はい、可能です。保守的なロジックはチューリング完全です。

2.保守的なロジックを実装できる物理的な影響はありますか？ はい、電子素子（個別のL / R / C素子に加えてMOSトランジスタ）に基づいて実装できます（実際には、2011年までにすべてが紙と研究所にのみ残っています - 約 ）

3.廃棄物を処理するために必要なエネルギーは、保守的なロジックへの移行から得られる潜在的な利益よりも大きくなりますか？ 特定の物理モデルを考慮せずにこの質問に対する完全な答えを出すことはできませんが、セクション4で説明する排水溝を隠す方法では、（楽観的な意味で）否定的な答えを得る可能性が非常に高くなります。

4.最後に、システムの低ノイズに対する安定性の問題は未解決のままです。

結論の代わりに（翻訳者から）

入力と出力の間のバンドルまたはケーブル内の配線を制御して混合し、「オーバーラップ」とリピーター以外の要素を使用しないことにより、出力の入力から関数を計算した結果を得ることができるという事実は明らかではありません。 基礎となる計算ロジックは異常ですが、マルコフアルゴリズムなどの他のチューリング完全な数学的抽象化とは異なり、非常に「技術的」に見え、実際のプロセッサですぐに使用できます。 おそらく、量子コンピューターは、純粋に量子の「トリック」に合わせて調整された同様の何かで動作するでしょう。 保守的な量子論理と超伝導相互接続を組み合わせると、実際にエネルギーを吸収しないコンピューターを構築できます。 さて、将来が表示されます。