Geekly Articles each Day

テキストと辞書のあいまい検索

はじめに


ファジー検索アルゴリズム（ 類似検索またはファジー文字列検索 とも呼ばれます ）は、スペルチェックシステムおよびGoogleやYandexなどの本格的な検索エンジンの基礎です。 たとえば、このようなアルゴリズムは、同じ検索エンジンの「おそらく...」などの機能に使用されます。

このレビュー記事では、次の概念、方法、アルゴリズムを検討します。
また、アルゴリズムの品質とパフォーマンスの比較テストも実施します。

だから...


ファジー検索は、検索エンジンの非常に便利な機能です。 同時に、その効果的な実装は、完全一致による単純な検索の実装よりもはるかに複雑です。

ファジー検索問題は次のように定式化できます。
「指定された単語について、サイズnのテキストまたは辞書で、 kの可能な違いを考慮して、この単語に一致する（またはこの単語で始まる）すべての単語を検索します。」

たとえば、2つの可能性のあるエラーを考慮して「Machine」を照会する場合、「Machine」、「Makhina」、「Raspberry」、「Kalina」などの単語を検索します。

ファジー検索アルゴリズムは、2つの単語間の距離の関数であるメトリックによって特徴付けられます。これにより、特定のコンテキストの類似度を評価できます。 メトリックの厳密な数学的定義には、三角形の不等式条件（Xは単語のセット、pはメトリック）を満たす必要があります。

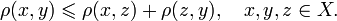
三角形の不等式

一方、ほとんどの場合、メトリックとは、そのような条件の充足を必要としないより一般的な概念を意味し、この概念は距離とも呼ばれます 。

最もよく知られている測定基準には、 ハミング 距離 、 レーベン シュタイン距離 、およびダメラウーレーベンシュタイン距離があります。 さらに、ハミング距離は同じ長さの単語のセットでのみのメトリックであり、その適用範囲を大幅に制限します。

ただし、実際には、ハミング距離は実際には役に立たないため、人間の観点からより自然なメトリックが得られます。これについては以下で説明します。

レーベンシュタイン距離


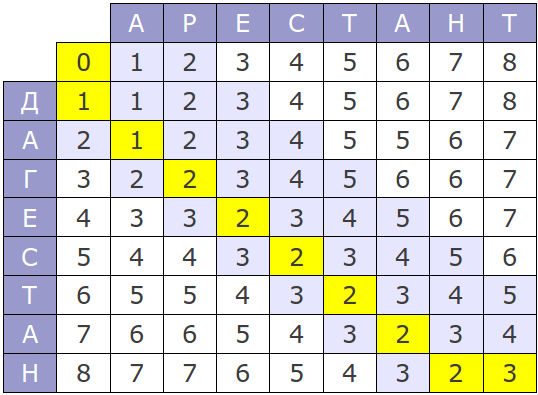
最も一般的に使用されるメトリックは、レーベンシュタイン距離または編集距離であり、その計算アルゴリズムはすべてのステップで見つけることができます。
それにもかかわらず、最も人気のある計算アルゴリズムであるワーグナー・フィッシャー法についてコメントする価値はあります。
このアルゴリズムの初期バージョンの時間の複雑さはO（mn）であり、 O（mn）メモリを消費します。ここで、 mとnは比較される文字列の長さです。 プロセス全体は、次のマトリックスで表すことができます。

レーベンシュタイン距離行列

アルゴリズムのプロセスを見ると、各ステップでマトリックスの最後の2行のみが使用されているため、メモリ消費をO（min（m、n））に減らすことができます。

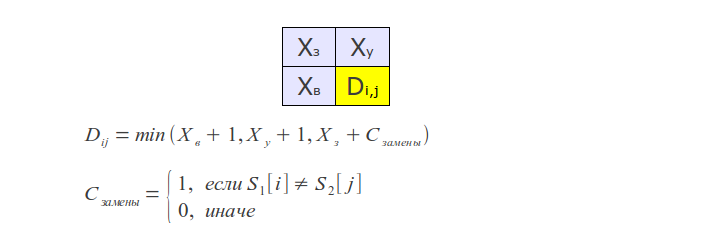
レーベンシュタインアルゴリズムの動作プロセス

しかし、これだけではありません。タスクがk個以下の違いを見つけることである場合、アルゴリズムをさらに最適化できます。 この場合、マトリックスで幅2k + 1 （Ukkonen cut-off）の対角ストリップのみを計算する必要があります。これにより、時間の複雑さがO（k min（m、n））に減少します。

プレフィックス距離

また、パターンプレフィックスと文字列の間の距離を計算する必要があります。つまり、指定されたプレフィックスと最も近い文字列プレフィックスの間の距離を見つけます。 この場合、サンプルプレフィックスからすべての回線プレフィックスまでの最小距離をとる必要があります。 明らかに、プレフィックス距離は厳密な数学的意味でのメトリックとは見なされず、その適用が制限されます。

多くの場合、ファジー検索では、距離自体ではなく、特定の値を超えるかどうかの事実が重要です。

距離Damerau-Levenshtein


このバリエーションは、レーベンシュタイン距離を決定する別のルールを導入します-挿入、削除、および置換とともに、2つの隣接する文字の転置 （再配置）も1つの操作として考慮されます。
数年前、フレデリック・ダメラウは、ほとんどのタイプミスが単なる転置であることを保証できました。 したがって、この特定のメトリックは、実際に最良の結果をもたらします。

Damerau-Levenshteinアルゴリズムプロセス

そのような距離を計算するには、通常のレーベンシュタイン距離を見つけるアルゴリズムを次のようにわずかに修正するだけで十分です：最後の2行ではなく、行列の最後の3行を保存し、対応する追加条件を追加します-転置の場合、距離を計算するときに、そのコストも考慮します

上記で説明した距離に加えて、Jaro-Winklerメトリックなど、実際に使用される距離は他にも多くあり、その多くはSimMetricsおよびSecondStringライブラリで利用できます 。

インデックスなしのファジー検索アルゴリズム（オンライン）


これらのアルゴリズムは、以前は未知のテキストで検索するように設計されており、たとえば、テキストエディター、ドキュメントを表示するプログラム、またはページで検索するWebブラウザーで使用できます。 テキストの前処理を必要とせず、データの連続ストリームを処理できます。

線形探索


入力テキストの単語への特定のメトリック（たとえば、レーベンシュタインメトリック）の単純な順次適用。 制限付きのメトリックを使用する場合、この方法により最適な速度を実現できます。 しかし、同時に、 kが大きいほど、動作時間が長くなります。 漸近時間推定はO（kn）です。

Bitap（Shift-OrまたはBaeza-Yates-Gonnetとも呼ばれ、Wu-Manberからの変更）


Bitapアルゴリズムとそのさまざまな変更は、インデックス付けなしのファジー検索に最もよく使用されます。 そのバリエーションは、たとえば、標準のgrepと同様の機能を実行するagrep unixユーティリティで使用されますが、検索クエリのエラーをサポートし、正規表現を適用する機会が限られています。

このアルゴリズムのアイデアは、1992年に記事を発表して、 リカルドバエザイェイツとガストンゴネットの市民によって初めて提案されました。
アルゴリズムの元のバージョンは、文字の置換のみを扱い、実際、 ハミング距離を計算します。 しかし、少し後で、 Sun WuとUdi Manberは、このアルゴリズムを修正して、 レーベンシュタイン距離を計算することを提案しました。 挿入と削除のサポートをもたらし、それに基づいてagrepユーティリティの最初のバージョンを開発しました。

操作ビットシフト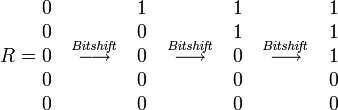

操作ビットシフト

挿入物
挿入物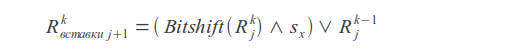
削除
削除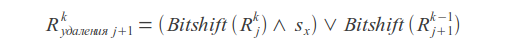
代替品
代替品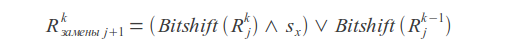
結果の値
結果

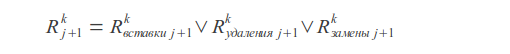
ここで、 kはエラー数、 jはシンボルインデックス、 s xはシンボルマスクです（マスクでは、ユニットビットはリクエスト内のこのシンボルの位置に対応する位置にあります）。
クエリの一致または不一致は、結果のベクトルRの最新のビットによって決まります。

このアルゴリズムの高速性は、ビット単位の計算の並列処理によって保証されます。1回の操作で、一度に32ビット以上の計算を実行できます。
さらに、単純な実装では、32以下の単語の検索がサポートされます。この制限は、標準のint型の幅（32ビットアーキテクチャ）によって決まります。 大きな次元のタイプを使用できますが、これによりアルゴリズムの動作がある程度遅くなる可能性があります。

このアルゴリズムO（kn）の漸近的な実行時間は線形法のそれと一致するという事実にもかかわらず、それは長いクエリではるかに速く、エラー数kは 2以上です。

テスト中


テストは320万語のテキストで実行され、平均語長は10です。

完全一致検索
検索時間：3562ミリ秒

レーベンシュタインメトリックを使用した検索
k = 2での検索時間：5728 ms
k = 5での検索時間：8385 ms

Wu-Manberを変更したBitapアルゴリズムを使用した検索
k = 2での検索時間：5499 ms
k = 5での検索時間：5928ミリ秒

明らかに、メトリックを使用した単純な検索は、Bitapアルゴリズムとは対照的に、エラー数kに大きく依存しています。

それでも、大量の未変更のテキストを検索する場合、そのようなテキストを前処理してインデックス付けとも呼ばれることにより、検索時間を大幅に短縮できます。

インデックス付きのファジー検索アルゴリズム（オフライン）


インデックス付きのすべてのファジー検索アルゴリズムの機能は、ソーステキストまたはデータベース内のレコードのリストからコンパイルされた辞書を使用してインデックスが構築されることです。

これらのアルゴリズムは、問題を解決するためにさまざまなアプローチを使用します-それらのいくつかは正確な検索への縮小を使用し、他はさまざまな空間構造などを構築するためにメトリックのプロパティを使用します。

まず、最初のステップで、テキスト内の単語とその位置を含む辞書がソーステキスト上に構築されます。 単語やフレーズの頻度をカウントして、検索結果の品質を向上させることもできます。

ディクショナリと同様に、インデックスは完全にメモリにロードされると想定されています。

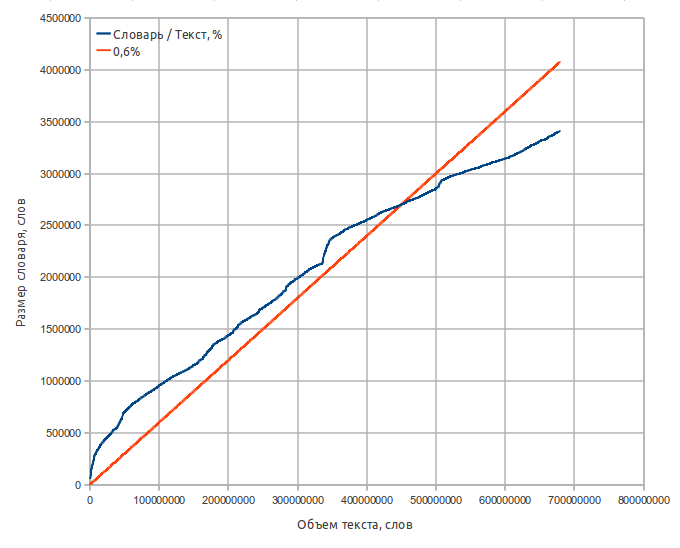
辞書のパフォーマンス特性：辞書のサイズのテキストのボリュームへの依存は厳密には線形ではありません-特定のボリュームまで、50万語で15％から500万で5％の範囲の単語の基本フレームが形成され、その後依存は線形に近づき、徐々に減少して680までに0.5％に達します百万語。 ほとんどの場合、まれな言葉が原因で成長の保存が保証されます。

辞書の成長

サンプリング拡張アルゴリズム


このアルゴリズムは、辞書のサイズが小さい、または速度が主要な基準ではない、スペルチェックシステム（つまり、スペルチェッカー）でよく使用されます。
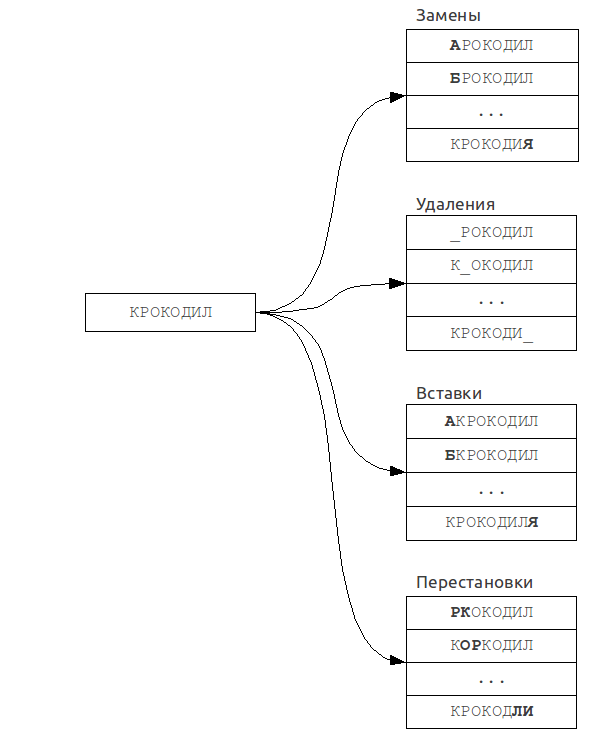
これは、ファジー検索問題を正確な検索問題に減らすことに基づいています。

多くの「誤った」単語が最初のクエリから作成され、それぞれに対して辞書での正確な検索が実行されます。

サンプル拡張

その動作時間は、kエラーの数とアルファベットAのサイズに大きく依存し、バイナリ辞書検索を使用する場合は次のようになります。
画像

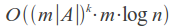
たとえば、ロシア語のアルファベットのk = 1および長さ7の単語（たとえば、「ワニ」）の場合、多くの誤った単語のサイズは約450になります。つまり、辞書に対する450のクエリを作成する必要があります。
しかし、 k = 2の場合でも、そのようなセットのサイズは11万5000を超えるオプションになります。これは、小さな辞書の完全な検索、またはこの場合は1/27の検索に対応するため、操作時間は非常に長くなります。 同時に、これらの単語のそれぞれについて、辞書で完全に一致するものを検索する必要があることを忘れてはなりません。

機能：
このアルゴリズムは、任意のルールに従って「誤った」オプションを生成するように簡単に変更でき、さらに、辞書の予備処理、したがって追加のメモリを必要としません。

可能な改善：
多くの「誤った」単語をすべて生成することはできませんが、実際の状況で発生する可能性が最も高いもの、たとえば、一般的なスペルミスやタイプミスを考慮した単語のみを生成できます。

N-gram法


この方法は長い間発明されており、その実装は非常に単純であり、十分なパフォーマンスを提供するため、最も広く使用されています。 アルゴリズムは次の原則に基づいています。
「いくつかのエラーを考慮して、単語Aが単語Bと一致する場合、高度の確率で、長さNの少なくとも1つの共通部分文字列があります。」
長さNのこれらの部分文字列はN-gramと呼ばれます。
インデックス作成中に、単語はそのようなN-gramに分割され、このN-gramごとにこの単語がリストされます。 検索中、クエリはN-gramにも分割され、それぞれについて、そのような部分文字列を含む単語のリストの順次検索が実行されます。

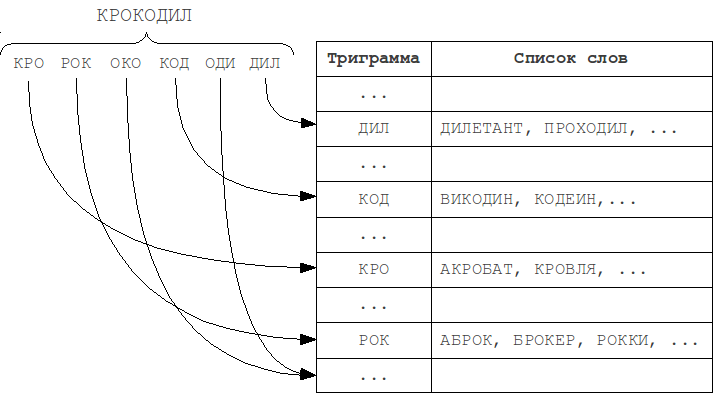
N-gram法

実際に最も一般的に使用されるのは、長さ3の部分文字列であるトライグラムです。Nの値を大きくすると、エラー検出が既に可能な最小語長が制限されます。

機能：
N-gramアルゴリズムは、エラーのある可能性のあるすべての単語を見つけるわけではありません。 たとえば、VOTKAという単語を取り、それをトリグラムに分解すると、TOT→TOTTKTAにすべてエラーTが含まれていることがわかります。したがって、「VODKA」という単語は見つかりません。これらのトライグラムは含まれておらず、それぞれのリストに含まれていません。 したがって、語長が短く、エラーが多いほど、要求のNグラムに対応するリストに該当せず、結果として存在しない可能性が高くなります。

一方、N-gramメソッドは、任意のプロパティと複雑さを備えた独自のメトリックを使用するための完全な範囲を残していますが、それを支払う必要があります-それを使用するときは、辞書の約15％を順番に検索する必要があります。これは、大きな辞書にはかなり多くあります

可能な改善：
N-gramのハッシュテーブルは、単語の長さおよび単語内のN-gramの位置で分割できます（変更1）。 検索された単語とクエリの長​​さがkを超えて異なることはできないのと同様に、単語内のN-gramの位置はkを超えて異なることができません。 したがって、単語内のこのN-gramの位置に対応するテーブルだけでなく、左側のk個のテーブルと右側のk個のテーブルだけをチェックする必要があります。 2k + 1個の隣接テーブルのみ。

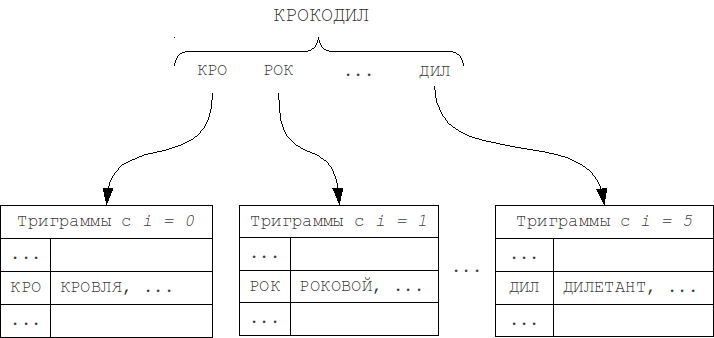
1 N-gramメソッドの変更

単語の長さでテーブルを分割し、同様に隣接する2k + 1テーブルのみを見ると（変更2）、表示に必要なセットのサイズを小さくすることができます。

署名ハッシュ


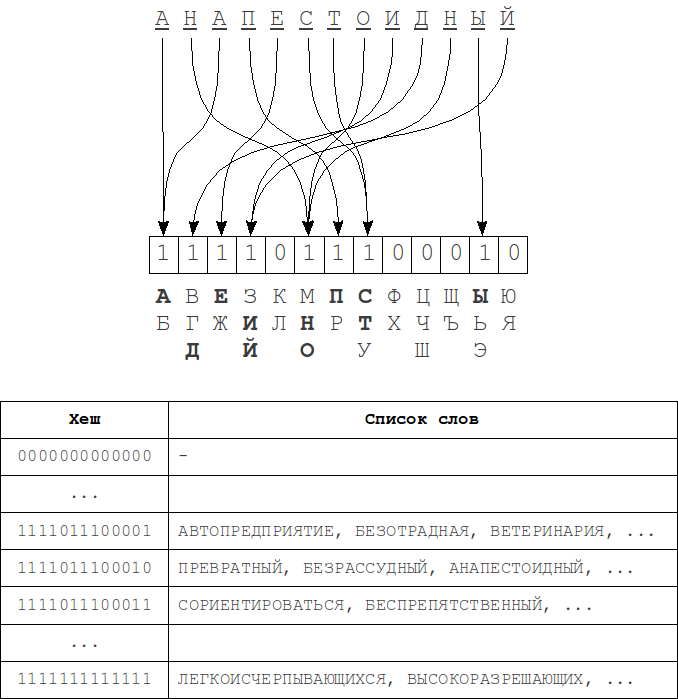
このアルゴリズムは、L。Boytsovによる記事に記載されています。 「署名によるハッシュ。」 これは、ビットテーブル形式のハッシュ（署名）として使用されるビットビット形式の「構造」という単語のかなり明白な表現に基づいています。

インデックスを作成する場合、そのようなハッシュは単語ごとに計算され、辞書の単語のリストとこのハッシュの対応がテーブルに入力されます。 次に、検索中に、リクエストのハッシュが計算され、kビット以下で元のハッシュと異なるすべての隣接ハッシュがソートされます。 これらの各ハッシュに対して、それに対応する単語のリストが列挙されます。

ハッシュ計算プロセス-ハッシュの各ビットは、アルファベットの文字グループに関連付けられています。 ハッシュの位置iのビット1は、元の単語にアルファベットのi番目のグループの文字があることを意味します。 単語内の文字の順序にはまったく意味がありません。

署名ハッシュ

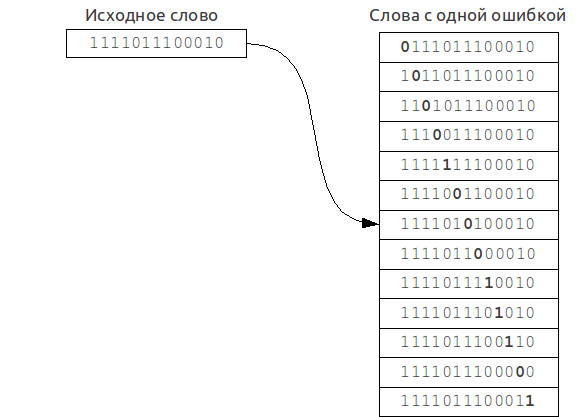
1文字を削除しても、ハッシュ値は変更されません（単語に同じアルファベットグループの文字がまだある場合）、またはこのグループに対応するビットは0に変更されます。同様に、挿入されると、1ビットが1になるか、変更がありません。 文字を置換する場合、すべてが少し複雑になります-ハッシュはまったく変更されないか、1か2の位置で変更されます。 先に述べたように、ハッシュの構築における文字の順序は考慮されないため、再配置するとき、変更はまったく行われません。 したがって、k個のエラーを完全にカバーするには、ハッシュ内の少なくとも2kビットを変更する必要があります。

エラーのあるハッシュのリスト

平均「k」の「不完全」（挿入、削除、転置、および置換の一部）エラーを伴う稼働時間：
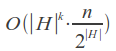
漸近的署名ハッシュランタイム

機能：
1つの文字を置き換えると2ビットが一度に変更される可能性があるため、たとえば、一度に2ビット以下の歪みを実装するアルゴリズムでは、実際には単語の重要な部分（ハッシュサイズとアルファベットの比率に依存）が不足しているため、結果の全量が生成されません2回の置換（およびハッシュサイズが大きくなると、文字の置換が一度に2ビットの歪みにつながることが多くなり、結果の完成度が低くなります）。 さらに、このアルゴリズムはプレフィックス検索を許可しません。

BKの木


Burkhard-Kellerツリーはメトリックツリーであり、そのようなツリーを構築するアルゴリズムは、三角形の不等式に対応するメトリックのプロパティに基づいています。

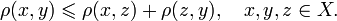
三角形の不等式

このプロパティにより、メトリックは任意のディメンションのメトリックスペースを形成できます。 そのような計量空間は必ずしもユークリッドではありません。たとえば、 レーベンシュタイン計量およびダメラウ-レーベンシュタイン計量は非ユークリッド空間を形成します。 これらのプロパティに基づいて、Barkhard-Kellerツリーであるこのようなメトリック空間で検索するデータ構造を構築できます。

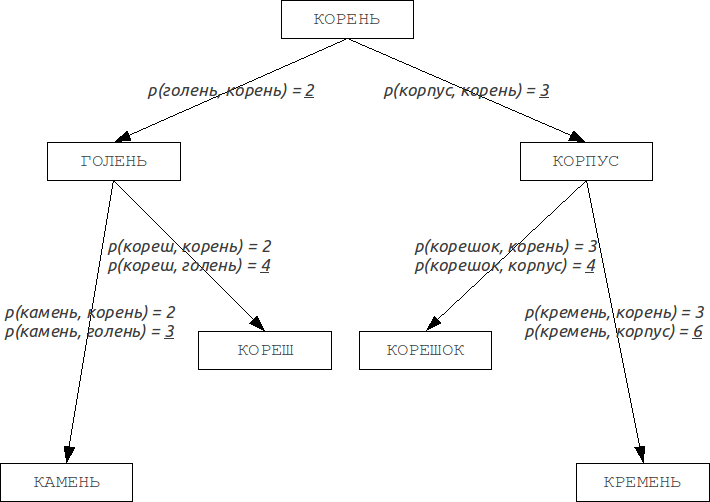
BKツリー

改善点：
一部のメトリックの機能を使用して、頂点の子孫までの最大距離と結果の距離の合計に等しい上限を設定することにより、制約された距離を計算できます。これにより、プロセスが少し速くなります。

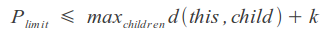
BKツリーアルゴリズムのメトリック制約

テスト中


テストは、Intel Core Duo T2500（2GHz / 667MHz FSB / 2MB）、2Gb RAM、OS-Ubuntu 10.10 Desktop i686、JRE-OpenJDK 6 Update 20を搭載したラップトップで実行されました。

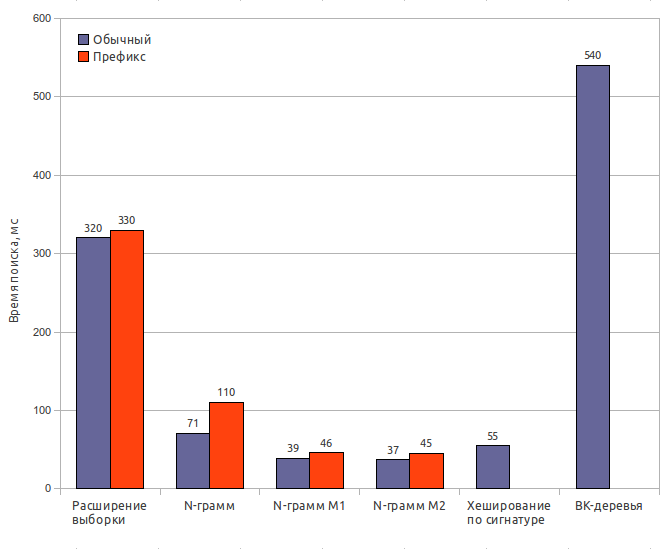
ランタイム比較

Damerau-Levenshtein距離とエラー数k = 2を使用してテストを実行しました。 インデックスのサイズは辞書で示されます（65 MB）。

サンプル拡張
インデックスサイズ：65 MB
検索時間：320 ms / 330 ms
結果の完全性：100％

N-gram（オリジナル）
インデックスサイズ：170 MB
インデックス作成時間：32秒
検索時間：71 ms / 110 ms
結果の完全性：65％

N-gram（変更1）
インデックスサイズ：170 MB
インデックス作成時間：32秒
検索時間：39 ms / 46 ms
結果の完全性：63％

N-gram（変更2）
インデックスサイズ：170 MB
インデックス作成時間：32秒
検索時間：37 ms / 45 ms
結果の完全性：62％

署名ハッシュ
インデックスサイズ：85 MB
インデックス作成時間：0.6秒
検索時間：55ミリ秒
結果の完全性：56.5％

BKの木
インデックスサイズ：150 MB
インデックス作成時間：120秒
検索時間：540ミリ秒
結果の完全性：63％

合計


インデックス付きのファジー検索アルゴリズムのほとんどは、真に準線形ではありません（つまり、漸近的な実行時間O（log n）以下）であり、それらの動作速度は通常Nに直接依存します それにもかかわらず、多数の改善と改善により、非常に大量の辞書があっても十分に短い時間を達成することができます。

また、この主題分野の他の場所で既に使用されているさまざまな技術の適応に基づいた、より多様で効果のない方法も数多くあります。 これらの方法の中には、 プレフィックスツリー（Trie）のファジー検索タスクへの適応があります 。これは、効率が低いために無人でした。 しかし、独自のアプローチに基づくアルゴリズムもあります。たとえば、 Maass-Novakアルゴリズムは、準線形漸近実行時間を持ちますが、そのような時間推定の背後に隠れている巨大な定数のために非常に非効率的であり、巨大なインデックスサイズとして表示されます。

実際の検索エンジンでのファジー検索アルゴリズムの実際の使用は、 音声アルゴリズム 、語彙ステミングアルゴリズム-同じ単語の異なる単語形式の基本部分の強調（たとえば、 SnowballとYandex mystemによって提供される機能）、および統計情報に基づくランキングに密接に関連しています、または洗練された高度なメトリックを使用します。

私のJava実装はhttp://code.google.com/p/fuzzy-search-toolsで見つけることができます：コードを理解しやすく、しかも実用に十分なほど効果的にしたかったのです。 JVMから最後のジュースを絞るのは私の仕事ではありませんでした。 お楽しみください。

このトピックを研究する過程で、インデックスのサイズが緩やかに増加し、メトリックの選択の自由が制限されているため、検索時間を大幅に短縮できる独自の開発がいくつかあったことは注目に値します。 しかし、これはまったく異なる話です。

参照：

  1. Javaの記事のソースコード。 http://code.google.com/p/fuzzy-search-tools
  2. レーベンシュタイン距離。 http://ru.wikipedia.org/wiki/Levenshtein_Distance
  3. 距離Damerau-Levenshtein。 http://en.wikipedia.org/wiki/Damerau–Levenshtein_distance
  4. ただし、Wu-Manberを変更したShift-Orのドイツ語の説明。 http://de.wikipedia.org/wiki/Baeza-Yates-Gonnet-Algorithmus
  5. N-gramメソッド。 http://www.cs.helsinki.fi/u/ukkonen/TCS92.pdf
  6. 署名ハッシュ。 http://itman.narod.ru/articles/rtf/confart.zip
  7. Leonid Moiseevich Boytsovのサイト。完全にあいまい検索専用です。 http://itman.narod.ru/
  8. Shift-Orおよびその他のアルゴリズムの実装。 http://johannburkard.de/software/stringsearch/
  9. Agrepを使用した高速テキスト検索（Wu＆Manber）。 http://www.at.php.net/utils/admin-tools/agrep/agrep.ps.1
  10. くそクールなアルゴリズム-レーベンシュタインのオートマトン、BKツリー、およびその他のアルゴリズム。 http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
  11. JavaのBKツリー。 http://code.google.com/p/java-bk-tree/
  12. Maass-Novakアルゴリズム。 http://yury.name/internet/09ia-seminar.ppt
  13. SimMetrics Metrics Library。 http://staffwww.dcs.shef.ac.uk/people/S.Chapman/simmetrics.html
  14. SecondStringメトリックライブラリ。 http://sourceforge.net/projects/secondstring/

ロシア語版： ファジー文字列検索

Source: https://habr.com/ru/post/J114997/

More articles:


All Articles