こんにちはコミュニティ! 多くの人が
接尾辞ツリーなどのデータ構造に精通していると思います。 Habréに
は、その構築方法とその理由の説明
がすでにありました。 つまり、所定の
テキスト Aで任意の
パターン X iを何度も検索する必要がある場合に必要であり、そのようなツリーはUkkonenアルゴリズムを使用して痛々しく構築されます(他のオプションもありますが、さらに苦しむことを示唆しています)。 アルゴリズムを使用する際の一般的な観察は、ツリーはもちろん良いことですが、実際には深刻なメモリオーバーヘッドと(コンピューターデータ操作の効率の観点から)最適ではない場所のために回避するのが最善です。 さらに、このようなツリーでは、さらに重大な迷惑、つまり構造のアルファベット順依存があります。 これらの問題を解決するために、
接尾辞配列が発明されました。 この記事では、ビルドの方法と使用方法について説明します。
この記事の内容は、
接尾辞と文字列
接頭辞の概念に関する知識、
および バイナリ検索の仕組みに関する知識を前提
としています。 また、
安定したソートと
ビット単位のソートが何であるかを理解する必要があります。また、カウントによる安定したソートの意味を理解する必要があります。 一部の部品については、セグメントの最小問題
-Range Minimum Query(RMQ)の知識が必要です。 まあ、一般的に、あなたは警告を受けました:誰もそれが簡単だとは言いませんでした。
サフィックスアレイアプリケーション
すべてのツリーが同じように役立つわけではありません。
だから、なぜ木は私たちに合わないのですか? まず、もちろん、子供や親などへのリンクを保存する必要があるためです。 この場合の使用メモリのサイズは、これらのリンクが保存されていない場合よりも著しく大きくなります。 第二に、いくつかの標準アロケータを使用してデータにメモリを割り当てると、「さまざまな角度で分散」します。ツリーを回る結果として、メモリキャッシュに影響する多数のメモリ遷移が想定されます。 もちろん、この問題を抑制できるトリックがあります。ツリーノードを配列に配置し、ポインターの代わりに配列のインデックスを使用する必要があります。 そうすると、ツリーはしっかりしたメモリのように見えます。
さて、これらはすべての木に共通の問題です。 そして、悪名高いアルファベット順の依存関係はどうですか? 接尾辞ツリーの実用的な実装を見てみましょう(これに遭遇していない場合、これは問題の本質を理解するために重要ではありません)。 そのようなツリーの各ノードには、1から(たとえば、分岐のない終端頂点の)アルファベットのサイズまでの子へのリンクがあります。 したがって、問題はこれらのリンクを保存する方法です。 たとえば、各ノードでアルファベットのサイズのリンクの配列を保持できます。 これはすぐに動作します-このノードに対応する子があるかどうかを調べるには、O(1)を使用できます。 しかし、配列のほとんどのセルにはゼロ参照が保存され、これらのセルのメモリはなくなります。 小さなアルファベット(DNAのヌクレオチドなど)の場合、それは地獄ですが、漢字を想像してみてください。 原則として、遠くに行く必要はありません。大文字と小文字を区別するロシア語のアルファベットでさえ考えさせませんが、空のデータを大量に取得したいかどうか。
動的に変化する配列(ベクトル)に空でないリンクのみを配置することにより、メモリをより経済的に使用できますが、O(1)の対応する子ノードの存在の確認は非常に疑わしくなります。 リンクをソートされた形式で保存する場合、O(ログ(アルファベットサイズ))。 ハッシュテーブルを試してみることができますが、これは非常に大きなアルファベットに対してのみ意味があり、さらに、別のレベルの間接参照が導入されます。 そして、そのような木を構築することはもはやO(n)ではありません。 一般に、いずれの場合でも、メモリとパフォーマンスの間で妥協する必要があります。
接尾辞配列
1989年、ManberとMyersは、接尾辞配列などのデータ構造と、それを使用して部分文字列を検索する方法を説明する記事を公開しました。
接尾辞配列は、辞書式にソートされた行の接尾
辞の配列です(用語がよくわからない場合は、
この記事の「問題の説明」セクションを
ご覧ください)。 一般的に、接尾辞自体を格納することは意味がありません。特定の接尾辞の先頭の位置を格納するだけで十分ですが、配列の定義を理解する方が簡単です。 文字列
「mississippi」の例を次に示します。
| # | 接尾辞 | サフィックス番号 |
|---|
| 1 | 私は | 11 |
| 2 | 一ッ | 8 |
| 3 | イシッピ | 5 |
| 4 | イシシッピ | 2 |
| 5 | ミシシッピ | 1 |
| 6 | パイ | 10 |
| 7 | ppi | 9 |
| 8 | シッピ | 7 |
| 9 | シシッピ | 4 |
| 10 | シッピー | 6 |
| 11 | シシッピ | 3 |
また、重要な概念は
接尾辞の
ランクです。つまり、接尾辞がソート時に取る場所、つまり接尾辞配列内の位置です。 これらは逆数です。 1つの配列を持っているので、O(N)のもう一方を取得できるので、それらを特に区別しません。したがって、常に両方を手元に置くことができます。

最も単純な部分文字列検索
例を考えてみましょう。 元の文字列は
"mississippi"です。
「一口」のサンプルが来たとしましょう。 接尾辞配列を使用してテキストにパターンが発生するかどうかを確認する最も簡単な方法は、パターンの最初の文字を取得し、
バイナリ検索 (配列がソートされる)を使用して、同じ文字で始まる接尾辞を持つ範囲を見つけることです。 範囲内のすべての要素が並べ替えられ、最初の文字が同じであるため、最初の文字を削除した後に残る接尾辞も並べ替えられます。 つまり、空の範囲が得られるか、パターン内のすべての文字が正常に見つかるまで、検索範囲を絞り込むプロセスを繰り返すことができます。 明らかに、このようにして、O(|
X | log |
A |)操作に対する答えが得られます。
| サンプル | IP | si p | 一口 |
|---|
| 私は | 私は | 私は |
| 一ッ | 一ッ | 一ッ |
| イシッピ | イシッピ | イシッピ |
| イシシッピ | イシシッピ | イシシッピ |
| ミシシッピ | ミシシッピ | ミシシッピ |
| パイ | パイ | パイ |
| ppi | ppi | ppi |
| s ippi | si ppi | 一口パイ |
| s issippi | シシッピ | シシッピ |
| s sippi | シッピー | シッピー |
| シシッピ | シシッピ | シシッピ |
バイナリ検索「正面」を使用する場合、まったく同じ複雑さを取得します:エッジに沿ったラインとサンプルの中央値の完全な辞書式比較:O(log |
A |)比較の平均「価格」との比較O(|
X |)。
より速く
悪くはないが、より良い。 実際、検索文字列全体を配列要素と比較する必要はありません。 バイナリ検索の各反復で、目的の要素を配置できる特定の範囲を指定します。 この範囲のすべての行は、いくつかの点で似ています。 つまり、これらの行には、目的の行と共通のプレフィックスが付いている場合があります。範囲外の行には、共通のプレフィックスが含まれないためです(サンプルの既に処理された部分をプレフィックスの一部と見なさないという意味で)。
現在の範囲のエッジを持つ残りのサンプルの一般的なプレフィックスの長さを知っていると仮定しますl = lcp(
X 、
S [ L
] )およびr = lcp(
X 、
S [ R
] )左右のエッジ(
lcp-最長共通プレフィックス)。 最初のステートメントは、lcp範囲内の任意の行について、これら2つの数値の最小値以上であるということです。 そうでない場合、接頭辞の最初の部分を変更せずに、シンボルがパターンの対応するシンボルと最初に一致し、次に一致せず、再び一致する位置があります。 これは、範囲のソートと矛盾します。 このアイデアを後から当たり前のように使用するので、このアイデアについて良い感触を得ることが重要です。 2番目のステートメントは明らかです。サンプルと範囲内の任意の行の共通プレフィックスがm = min(l、r)以上の場合、m文字はすぐにスキップされ、いずれの場合でも一致していることを認識し、m + 1からのみ比較します(そして特定の行のlcpになります)。
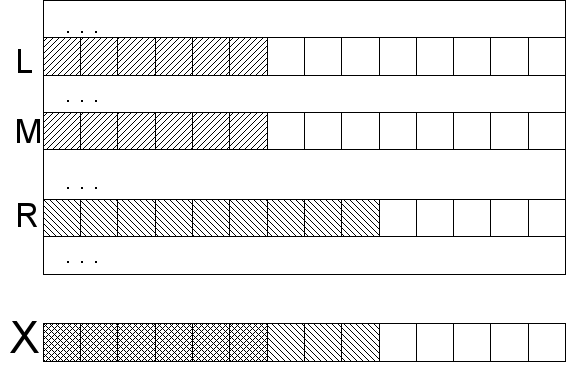
したがって、文字列「額」のバイナリ検索で最適化された文字列比較を適用します。 最悪の場合、もちろんこれから恩恵を受けることはありません:目的の要素が配列の端にあるが、隣同士がlcpでまったく類似していない場合、r(またはl)は毎回小さくなり、mも小さくなります。つまり、それぞれをチェックする必要がありますログごとの文字|
A | 回。 しかし、実験結果によると、自然なテキストの場合、検索時間はO(log |
A ||
X |)に比べて大幅に短縮されますが、特定の漸近現象について言うのは困難です。
原則として、実用的なアプリケーションではすでにこれで十分ですが、すべてを絞る場合は...
さらに速く
これは制限ではありません。 配列セクションの端の位置はこのセクションの中心を定義し、バイナリ検索で実装されるこのような構成はすべて、固定サイズセットのサブセットです。
A | -2。 これらの構成でm
l = lcp(
S [ M
] 、
S [ L
] )およびm
r = lcp(
S [ M
] 、
S [ R
] )の量を事前に計算したと仮定します。ここでMはLとRの間のセクションの中央です。これは、バイナリ検索ステップで行います。
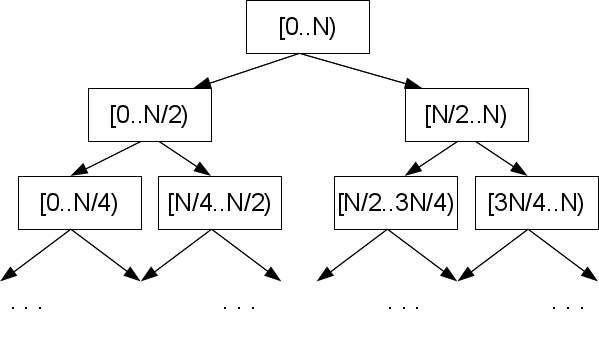
エッジの1つ、たとえば左側を見てみましょう。 l <m
lを計算した場合、左端は中央(およびそれらの間の任意の要素)に私たちが望むよりもはるかに強く、比較結果はLとMの間のセクション全体で事前にわかっています:lcp(
X 、
S [ M
] )= l。 このことから、求められている要素がこのセクションにないことはすぐに明らかであり、探している場合は反対の半分にあります。 l> m
lの場合、中央は目的のサンプルよりも小さい左端に似ています。 したがって、lcp(
X 、
S [ M
] )= m
l 、およびその間のどこかに目的の要素を探す必要があります。
当然、左端を右端に置き換えても、推論に変化はありません。 1つのケースのみが考慮されませんでした:l = m
lおよびr = m
r (少なくとも1つの等式が真でない場合、結果は前の段落に従って知られています)。 それから、lcp(
X 、
S [ M
] )がmax(l、r)より小さくないことは明らかです。しかし、その正確な定義と、文字を比較する必要がある方法を見つけるために(最終的に!)位置max(l、r )+1。
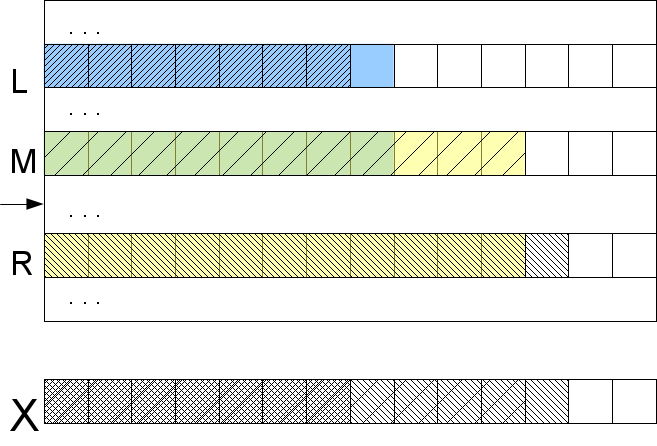
何を得たの? いくつかのlcpを相互に比較することにより、バイナリ検索ステップの一部を実行します。文字を比較する場合でも、文字
Xごとに1回のみです(max(l、r)+1を取ります。これは決して戻らないことを意味します)。 したがって、
最悪の場合のO(log |
A | + |
X |)アルゴリズムの複雑さを取得します。 確かに、バイナリ検索アルゴリズムによって誘導された検索ツリーで見つかったテキスト
Aの接尾辞には、事前に計算されたlcpが必要です。
m
rがわからないが、m
lしかわからない場合は、心配する必要はありません。 エントリがないと事前に言う機会はありませんが、これは複雑さを悪化させることはありません。右端だけを見て、左端だけを見ます。 l <m
lの場合、残りの半分をさらに調べ、l> m
lの場合はlを保存し、rをm
lとしてこの半分を調べますが、l = m
lの場合、中央値要素を目的の文字列と比較しますl + 1番目の位置から開始します。 この場合も戻りません。つまり、アルゴリズムの複雑さを損なうことなく、左端に対してのみlcpを実行できます。
LCP前処理
覚えているように、効果的な部分文字列検索には、サフィックスの特定の組み合わせに対して事前に計算されたlcpが必要でした。 それらを取得する方法を説明する必要があります。 これらの方法は通常、セグメントの最小値を見つける問題RMQに帰着するため、アルゴリズムのアルゴリズムの複雑さは、RMQ問題をどれだけ効率的に解決できるかに大きく依存します。 多かれ少なかれ単純なアルゴリズムは、前処理でO(NlogN)、要求でO(1)かかります。 つまり、O(NlogN)で接尾辞配列の構築を使用する場合、それを使用することはかなり可能です。 もちろん、線形時間で接尾辞配列を作成する場合は、一定のクエリで線形時間にRMQ前処理アルゴリズムを使用する必要があります。
まず、いわゆるlcp配列を作成します-これは、辞書的に隣接するサフィックス間のlcp値の配列です(サフィックス配列を作成した後、どのサフィックスが隣接する質問を引き起こさないか)。 lcp配列がある場合、2つの要素間でlcpを見つけると、lcp配列の指定されたセグメントの最小値、つまり純粋な形式のRMQタスク-セグメントの最小値を見つけることになります。 なぜこれがそうなのかは、接尾辞の順序の考慮から明らかです:2行の間にlcpがさらにある場合、それらの間のすべての行には少なくとも同じ数の同じ文字が先頭に含まれ、これらの行の間のすべてのlcpは極端な相互のlcp以上になります要素。
lcp配列の構築は非常に簡単です。 もちろん、接尾辞配列を通過し、隣接する要素のlcpをカウントすることは機能しません-これはO(N
2 )です。 ただし、正しい順序で配列を調べれば、前の手順の情報を計算に使用できます。 つまり、元の行に現れる順序でサフィックスを並べ替える場合、各ステップでlcpは前のステップと比較して1を超えて減少することはできません。つまり、それよりも多く、変化しない場合がありますが、 less then only1。これは次の理由で起こります。 lcp(
A [i ..]、
A [j ..])= lであることがわかった場合、最初の文字をドロップすると、明らかに1つ減ります:lcp(
A [i + 1 ..]、
A [j +1 ..])= l-1。 もちろん、i番目とj番目の接尾辞が辞書式に隣接していることが判明した場合、i + 1番目とj + 1番目が隣接することは保証されません。 しかし、すでにわかっているように、それらの間のlcpは、それらの間のセグメント全体の最小lcpです。つまり、i + 1番目の接尾辞と辞書式の後に続くlcpはl-1以上です。
| # | 接尾辞 | ステップ | lcp |
|---|
| 1 | 私は | 10 | 1 |
| 2 | 一ッ | 7 | 1 |
| 3 | イシッピ | 4 | 4 |
| 4 | イシシッピ | 2 | 0 |
| 5 | ミシシッピ | 1 | 0 |
| 6 | パイ | 9 | 1 |
| 7 | ppi | 8 | 0 |
| 8 | シッピ | 6 | 2 |
| 9 | シシッピ | 3 | 1 |
| 10 | シッピー | 5 | 3 |
| 11 | シシッピ | 飛ばす | |
これにより、すべての文字をスキップして最後から2番目(l-1)にすることができます。これは、それらが等しいことを確認し、l番目以降の文字のみを比較するためです。 これは、チェックを行うと、現在のlcpが増加するか、強制的に次の反復に進むことを意味します。 したがって、辞書的に最後の接尾辞を除くすべての接尾辞を渡すと(省略される必要があります)、線形時間O(N)のlcp配列を取得します。
まあ、それだけです。 必要なサフィックスのペアのRMQを見つけることは残っています。 RMQソリューションは、前処理と、実際には要素間の最小クエリへの応答で構成されています。 主な計算負荷は前処理にあり、クエリの実行はO(1)で行えるため、一般的に言えば、任意のサフィックスのlcpについてO(1)に答えることができるため、関心のあるペアとそれらの間のlcpを明示的に書き出す必要はありません、バイナリ検索で役割を果たすものを含む。 これにより、保存された値の対処方法を考える必要がなくなるため、これは非常にクールです。 まだ計算済みの形式でlcpを保存する場合は、検索ツリーの状態に正しく番号を付ける必要があります。メモリ内の場所とバイナリヒープ内のアドレスについて読んでください。
私はRMQの解決方法については書きません-HabréにはO(NlogN)の簡単なバージョンに関する良い
記事が既にありました。そして、O(N)のハードコアバージョン-Farah
-Coltonアルゴリズムとベンダーサフィックス配列の構築
さて、ここで接尾辞配列を適用する方法を知っていますが、それはどこから来るのでしょうか? 明らかに、接尾辞をソートする直接的な方法でそれを構築することは長いビジネスです-O(N
2 logN)、ここでN = |
A |。 O(NlogN)で機能するアルゴリズムは多数ありますが、O(Nlog)で機能するアルゴリズムもあります。 O(N)が非常に紛らわしい(たとえば、最初にサフィックスツリーを構築し、次にそこからサフィックス配列を収集するなど)。 特定のタスクの最大効率がそれほど重要でない場合は、コードのわかりやすさを考慮して、NlogNオプションで停止する必要があります。 次に、これらのカテゴリから1つの実行アルゴリズムを使用します。
O(NlogN)あたり
ビット単位の並べ替えの仕組みを思い出してください。まず、下位に基づいてカウントすることで要素をバケットに分配し、次に次のビットで同じことを行います。 ここでは、同様の動作をしますが、まだ少し異なります-ビット単位の並べ替えをサフィックスに直接適用すると、O(N
2 )が得られます。
あるステップで、最初の文字Hに従って行をソート(またはバケットに配置)するとします。 行のこれらの部分にバスケットの番号を付けることができます。 しかし、各接尾辞
S [ i
] =
A [ i ..
]は、配列の要素としてだけでなく、配列の他の要素の一部として、特に接尾辞
S [ iH
]の位置Hの部分文字列としても見られ
ます (わかりやすくするために、末尾の境界効果を省略します)文字列-目的の数のセンチネルを最後まで書き込むことで回避できます)。 つまり、最初のHサフィックス文字にバスケット番号を付けて、2番目のH文字にも自動的に番号を付けます。 次に、(あるステップの)バスケット番号で構成されるペアのセットを取得します。 これらのペアをビット単位のソートでソートすると、2Hの最初の文字でバスケットに詰め込まれた行のO(N)が得られます。 したがって、各ステップで処理される文字の数は2倍になります。 これにより、O(logN)ステップとO(NlogN)アルゴリズムの全体的な複雑さが与えられます。

最初のステップに関する別の小さなコメント。 次のステップでバスケット番号をソートする必要があり、それがビットごとのソートで問題を引き起こさない場合、最初のステップは最初の文字で行をソートすることです。 アルファベットの性質によっては、ビット単位の並べ替えができないことが判明する場合があります。 次に、O(NlogN)複雑度との比較に基づいて他のソートを適用し、O(N)を超えるバスケット範囲を見つけることができます。 これにより、アルゴリズムの全体的な複雑さは変わりません。
Oあたり(N)
これはKarkainenとSandersによって2003年に公開されたかなり新しいアルゴリズムです。 このアルゴリズムはアルファベットでのみ機能し、その文字はO(N)時間で番号付けできることをすぐに警告する必要があります(番号付けはソートと同等です。つまり、ビット単位のソートでO(N)でソートできる必要があります)。 その他はまれですが、それでも起こります。
アルゴリズムは再帰的です。つまり、ある段階で、長さが短い文字列の接尾辞配列を見つけるという同じ問題が発生します。
ミシシッピの例を考えてみましょう。 したがって、最初に行うことは、1〜Nの数字を使用してシンボルに番号を付け、数字のアルファベットに移動することです。 前述したように、これはO(N)ビット単位の並べ替えで実行できます。 その後、元の「実際の」文字には興味がなく、文字列の数値表現のみを使用します。 これは、かつては数値シーケンスではなかったことを忘れることができます。
次に、テキスト内のすべてのトライグラムを含むスーパーアルファベットを作成し、この新しいアルファベットの文字に辞書式順序で番号を付けます。 これらのトライグラムが文字列内の文字にすぎないことは明らかです(一致するものがある場合を除きます)。 このアルファベットを効果的に使用できるようにするため、毎回スーパーアルファベットでトライグラムを検索し、その辞書式位置(辞書式位置はランクとも呼ばれる)を返すオプションはロールしません。 どのようなトライグラムの問題がまったく発生しないように、すぐに上付き文字に番号を付ける必要があります。 これを行うには、入力行の各文字を一致させる必要があります(数字であるか、忘れていませんか?)この位置のトライグラム番号。 これは、元の行からのすべてのトライグラムを(複製とともに)ビットごとにソートし、トライグラムの元の位置を維持することによって行われます。 この場合の後続の番号付けは難しくありません。
たとえば、
A =
“ mississippi”から、トライグラム{mis、iss、ssi、... ppi、pi $、i $$}、および辞書式順序{i $$、ipp、iss、... ssi}を取得できます。 センチネルが必要に応じて行を補完し、それらを最小文字と見なします。
| 元の行: | m | 私は | s | s | 私は | s | s | 私は | p | p | 私は |
| 数値文字列: | 2 | 1 | 4 | 4 | 1 | 4 | 4 | 1 | 3 | 3 | 1 |
| トライグラム: | ミス | iss | ssi | sis | iss | ssi | 一口 | ipp | ppi | pi $ | 私は$$ |
| トリグラムの番号付け: | 4 | 3 | 9 | 8 | 3 | 9 | 7 | 2 | 6 | 5 | 1 |
この時点で、行のすべてのトライグラムが異なることが判明する場合があります。 トライグラムが異なる場合、辞書式順序が接尾辞の辞書式順序を決定するため、これは初期の終了条件として使用できます(この条件は使用できませんが、答えが明らかになるまで行を短いものに減らし続けるだけです)。 最初の文字列は、トライグラムの形式で3つの方法で表現できます。文字列自体をトリグラムに分割する、最初の文字のない文字列、最初の2文字のない文字列です。 文字列のこれらの表現をT
0 、T
1、およびT
2と呼びます。 それらのそれぞれは、オリジナルよりも3倍短いです。 ゼロから位置を数える場合、これらの表現は位置i mod 3 = 0、i mod 3 = 1およびi mod 3 = 2のサフィックスのグループに対応して呼び出すことができます。
| T 0 : | ミス | sis | 一口 | pi $ |
| 4 | 8 | 7 | 5 |
| T 1 : | iss | iss | ipp | 私は$$ |
| 3 | 3 | 2 | 1 |
| T 2 : | ssi | ssi | ppi | |
| 9 | 9 | 6 | |
次に、フェイントが耳で作られますが、その意味は後で明らかになります:具体的には、T
1とT
2の 3つの行のうち2つを、トライグラムの形で提示し、連結して、再帰呼び出しで同じアルゴリズムに渡します。 明らかに、送信される文字列の長さは元の文字列よりも1/3短くなります。 アルゴリズムの終了時には、接尾辞配列(または、同等のランクの配列)が必要です。 トライグラムから数行に戻ると、グループ1と2のサフィックス間の辞書式順序に関する情報が得られます。
グループ0の接尾辞は、シンボルとグループ1の接尾辞から成るペア、または2文字のトリプルとグループ2の接尾辞として表すことができます
。A [3k ..] =(A [3k]、
A [3k + 1 ..])= (A [3k]、A [3k + 1]、
A [3k + 2 ..])。 接尾辞の他のグループを隣接する接尾辞に変換するために、同様の式を書くことができます。 タイプ0の接尾辞をシンボルとタイプ1の接尾辞のペアとして表現します(より正確には、タイプ1の接尾辞のランク、接尾辞自体は私たちにとって興味深いものではありません)。
この段階で、相互にソートされたタイプ1および2のサフィックス、およびタイプ0のソートされたサフィックスの形式で再帰的な関数呼び出しの結果が得られます。タイプ0サフィックスをタイプ1と比較するには、タイプ0サフィックスをタイプ1に、タイプ1をタイプ2に変換する必要があります。(A [3l]、
A [3l + 1 ..])VS(A [3m + 1]、
A [3m + 2] ..)。 これらの2つのペアを比較するのは簡単です:最初の文字が順序を決定するか、等しい場合、順序はグループ1と2のサフィックスの順序を決定します。これは、このアルゴリズムの再帰呼び出しの結果からわかります。 タイプ0と2のサフィックスを比較するために、チェーンはわずかに大きくなりますが、本質は同じです:(A [3l]、A [3l + 1]、
A [3l + 2 ..])VS(A [3m + 2]、A [3 (m + 1)]、
A [3(m + 1)+1 ..])。
一見したところ、なぜこれがすべて線形の複雑さをもたらすのかは明らかではありません。 最初に、再帰呼び出しを除くすべてに対処します。 上付き文字のビット単位の並べ替え、マーキングサフィックスはすべてO(N)、グループ0のサフィックスのビット単位の並べ替えおよび並べ替えられた配列のマージもO(N)です。 再帰呼び出し-元の文字列の長さの2/3のアルゴリズムを呼び出すため、アルゴリズムの複雑さはT(N)= T(2N / 3)+ O(N)です。 この式を自分自身に代入してペイントすると、2/3の係数で等比数列の合計が得られるため、O(N)が制限されます。 したがって、結果の複雑さはO(N)です。
おわりに
これが、接尾辞配列の適用方法と構築方法です。 アルゴリズムは非常に膨大ですが、やるべきことは非常に高度なタスクです。 私はこれをかなり一般的な用語で説明しましたが、明らかな理由でコードを提供しませんでした-言葉とコードが多すぎるでしょう。 ご覧のように、アルゴリズムは高速であり、実装の複雑さの点でわずかに遅いため、O(N)ではなくO(N)の場合など、本当にこれを行う必要があるかどうかを何度も考える理由があります。
また、「完成した実装をどこで見ることができるか」、「もっと読む場所」などのような質問も予想しています。
ウィキペディアのページが存在すると主張しているが、私は個人的に「ただコンパレータを追加する」スタイルの既製の実装を見たことがない。
ここと
ここには説明と実装があります。 さらに、KarkainenとSanders
による元の記事にも配列構築コードがあります。 NlogNの構築については、ManberとMyersの記事で読むことができます。UdiManber、Gene Myers-「サフィックス配列:オンライン文字列検索の新しい方法」。