Habrのすべての読者への挨拶! この記事を書くことに決めたので、グラフ、特に
トポロジカルソートに関する多くの資料をHabréで見つけました。 たとえば、
ここでは理論的な部分
をかなり詳細に説明し、基本的なアルゴリズムの例を示します。 したがって、ここでは繰り返しませんが、
トポロジカルソートの実用的な応用分野について説明します。あるいは、
DevExpress製品を開発するときに、この方法で個人的な経験を共有したいと
思います。 この記事から、このアルゴリズムの使用を促した動機と理由が明らかになります。 最後に、依存オブジェクトをソートするためのアルゴリズムのバージョンを提供します。
DevExpressのソートアルゴリズムの範囲
前の記事で 、
XtraSchedulerスケジューラとその印刷拡張機能について説明しました。 視覚的な要素を扱うレポートデザイナーが含まれています。 デザイナーで印刷されたフォームの外観をデザインするとき、「主従」の原則に関するレポートの視覚要素間のリンクを確立する必要があります。 これらの依存関係により、要素間でのデータの転送方法が決まります。 内部実装の場合、これはこれらのオブジェクトの正しい印刷優先度の形成を意味します。
本質的な要素は、オブジェクトの有向グラフを表しています。 これらのコントロールのオプションは、メインオブジェクトへのリンクを設定することにより、依存関係の方向を一意に決定しました。
トポロジカルソートアルゴリズムは、依存オブジェクトを適切な順序で構築してから印刷し、それらの間の関係を分析するのに最適でした。 さらに、従属コントロールは、印刷時にメインコントロールのレンダリングデータを使用しました。 したがって、このアルゴリズムは、データおよび関連するサブリストに従って、メインのイテレータオブジェクトを含む内部データキャッシングオブジェクトを整理するためにも使用されました。
他にどこでアルゴリズムを適用しましたか?
少し後、
XtraRichEditプロジェクト
では、RTFおよびDOC形式のドキュメントのスタイルのインポートとエクスポートを開発するときに、依存関係を含むオブジェクトを正しい順序で受け取る必要もありました。 説明したアルゴリズムは一般化されており、この場合に正常に適用されました。
アルゴリズム-T
ソートアルゴリズムの実装に移りましょう。 これは
、 Donald Knuthの著書
「The Art of Programming」 (2.2.3章の第1巻)に記載されているAlgorithm-Tに基づいています。 したがって、元のアルゴリズムの詳細について読むことができます。ここでは、アイデアの一般的な理解のためにアルゴリズムの図のみを示します。
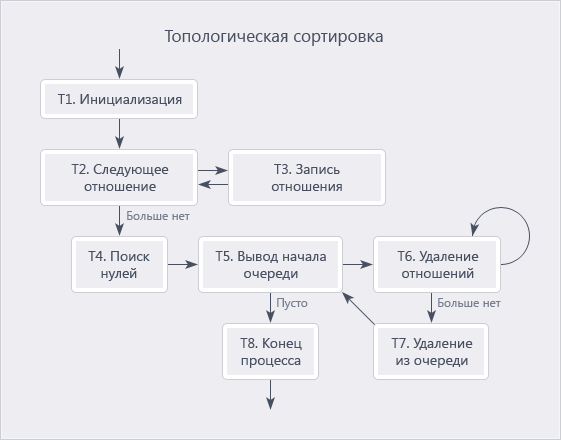
なぜこのアルゴリズムを選択したのですか? 著者に少し引用させてください。
「Tアルゴリズムの分析は、キルヒホッフの法則を使用して非常に簡単に行うことができます。 この法則を使用すると、実行時間は式c1 * m + c2 * nを使用して推定できます。ここで、mは入力された関係の数、nはオブジェクトの数、c1とc2は定数です。 この問題を解決するためのより高速なアルゴリズムを想像することは不可能です!」
実装されたアルゴリズムは、
Algorithmsクラスの
DevExpress.Data.dllアセンブリにあります。このクラスには、トポロジカルな並べ替えとともに、他の便利なアルゴリズムが含まれています。
namespace DevExpress.Utils { public static class Algorithms { public static IList<T> TopologicalSort<T>(IList<T> sourceObjects, IComparer<T> comparer) { TopologicalSorter<T> sorter = new TopologicalSorter<T>(); return sorter.Sort(sourceObjects, comparer); } }
アルゴリズムの使用は非常に簡単です。 クラスの静的メソッドを呼び出して、必要なパラメーターを渡すだけで十分です。 呼び出しの例は次のとおりです。
protected virtual IList<XRControl> SortControls(List<XRControl> sourceControls) { return Algorithms.TopologicalSort<XRControl>(sourceControls, new ReportViewControlComparer()); }
明示的にソーターオブジェクトのインスタンスを作成することにより、静的メソッドを呼び出さずに実行できます。
アルゴリズムを実装するソータークラスのソースコードは、記事の最後に記載されています。
パラメータからわかるように、オブジェクトのリストに加えて、特殊なコンパレータオブジェクトがメソッドに渡されます。 指定されていない場合、デフォルトのオブジェクトが使用されます。 実際には、比較オブジェクトは、比較対象オブジェクトのプロパティに基づいて比較ロジックが決定されるので、通常定義されます。 さらに、そのようなオブジェクトは、いくつかの継承された型に対して同時にいくつかのIComparerインターフェイスを実装できます。
このようなクラスの例として、
XtraScheduler.Reportingライブラリで使用されるReportViewControlComparerを提供します。
public class ReportViewControlComparer : IComparer<XRControl>, IComparer<ReportViewControlBase> { #region IComparer<XRControl> Members public int Compare(XRControl x, XRControl y) { return CompareCore(x as ReportRelatedControlBase, y as ReportViewControlBase); } #endregion #region IComparer<ReportViewControlBase> Members public int Compare(ReportViewControlBase x, ReportViewControlBase y) { return CompareCore(x as ReportRelatedControlBase, y); } #endregion int CompareCore(ReportRelatedControlBase slave, ReportViewControlBase master) { if (slave != null && master != null) { if (slave.LayoutOptionsHorizontal.MasterControl == master || slave.LayoutOptionsVertical.MasterControl == master) return 1; } return 0; } }
応用例
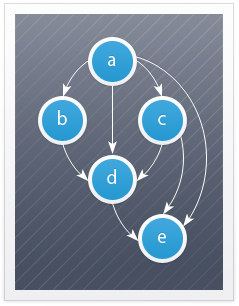
アルゴリズムの動作を示すために、コンソールアプリケーションを作成します。 グラフの例として、5つのノードの単純なグラフを取り上げます(記事の冒頭の図を参照)。
G =({a、b、c、d、e}、{(a、b)、(a、c)、(a、d)、(a、e)、(b、d)、(c、d )、(c、e)、(d、e)})グラフを表すために、関連する他のノードのリストでノードを定義する単純なクラスが使用されます。
public class GraphNode { List<GraphNode> linkedNodes = new List<GraphNode>(); object id; public GraphNode(object id) { this.id = id; } public List<GraphNode> LinkedNodes { get { return linkedNodes; } } public object Id { get { return id; } } }
アプリケーション自体のコードは次のとおりです。
class Program { static void Main(string[] args) { DoDXTopologicalSort(); } private static void DoDXTopologicalSort() { GraphNode[] list = PrepareNodes(); Console.WriteLine("DX Topological Sorter"); Console.WriteLine(new string('-', 21)); Console.WriteLine("Nodes:"); GraphNode[] list = PrepareNodes(); PrintNodes(list); IComparer<GraphNode> comparer = new GraphNodeComparer(); IList<GraphNode> sortedNodes = DevExpress.Utils.Algorithms.TopologicalSort<GraphNode>(list, comparer); Console.WriteLine("Sorted nodes:"); PrintNodes(sortedNodes); Console.Read(); } static GraphNode[] PrepareNodes() { GraphNode nodeA = new GraphNode("A"); GraphNode nodeB = new GraphNode("B"); GraphNode nodeC = new GraphNode("C"); GraphNode nodeD = new GraphNode("D"); GraphNode nodeE = new GraphNode("E"); nodeA.LinkedNodes.AddRange(new GraphNode[] { nodeB, nodeC, nodeE }); nodeB.LinkedNodes.Add(nodeD); nodeC.LinkedNodes.AddRange(new GraphNode[] { nodeD, nodeE }); nodeD.LinkedNodes.Add(nodeE); return new GraphNode[] { nodeD, nodeA, nodeC, nodeE, nodeB }; } static void PrintNodes(IList<GraphNode> list) { for (int i = 0; i < list.Count; i++) { string s = string.Empty; if (i > 0) s = "->"; s += list[i].Id.ToString(); Console.Write(s); } Console.WriteLine("\r\n"); } }
グラフの直接的な関係は
PrepareNodesメソッドで設定されます。 この場合、依存関係は任意に作成されます。
ノードを比較するには、GraphNodeComparerクラスも必要です。
public class GraphNodeComparer : IComparer<GraphNode> { public int Compare(GraphNode x, GraphNode y) { if (x.LinkedNodes.Contains(y)) return -1; if (y.LinkedNodes.Contains(x)) return 1; return 0; } }
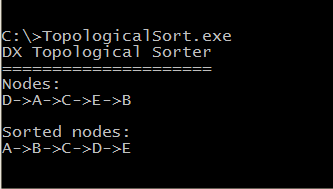
アプリケーションを起動した後、ノードのソートされたリストを取得し、コンソールが表示されます
A-> B-> C-> D-> Eプログラムの結果を次の図に示します。
ソーターソースコード
上記で約束したように、トポロジカルソートアルゴリズムの実装コードを提供します。
namespace DevExpress.Utils.Implementation {
#region TopologicalSorter
public class TopologicalSorter<T> {
#region Node
public class Node {
int refCount;
Node next;
public Node( int refCount, Node next) {
this .refCount = refCount;
this .next = next;
}
public int RefCount { get { return refCount; } }
public Node Next { get { return next; } }
}
#endregion
#region Fields
int [] qLink;
Node[] nodes;
IList<T> sourceObjects;
IComparer<T> comparer;
#endregion
#region Properties
protected internal Node[] Nodes { get { return nodes; } }
protected internal int [] QLink { get { return qLink; } }
protected IComparer<T> Comparer { get { return comparer; } }
protected internal IList<T> SourceObjects { get { return sourceObjects; } }
#endregion
protected IComparer<T> GetComparer() {
return Comparer != null ? Comparer : System.Collections. Generic .Comparer<T>.Default;
}
protected bool IsDependOn(T x, T y) {
return GetComparer().Compare(x, y) > 0;
}
public IList<T> Sort(IList<T> sourceObjects, IComparer<T> comparer) {
this .comparer = comparer;
return Sort(sourceObjects);
}
public IList<T> Sort(IList<T> sourceObjects) {
this .sourceObjects = sourceObjects;
int n = sourceObjects.Count;
if (n < 2)
return sourceObjects;
Initialize(n);
CalculateRelations(sourceObjects);
int r = FindNonRelatedNodeIndex();
IList<T> result = ProcessNodes(r);
return result.Count > 0 ? result : sourceObjects;
}
protected internal void Initialize( int n) {
int count = n + 1;
this .qLink = new int [count];
this .nodes = new Node[count];
}
protected internal void CalculateRelations(IList<T> sourceObjects) {
int n = sourceObjects.Count;
for ( int y = 0; y < n; y++) {
for ( int x = 0; x < n; x++) {
if (!IsDependOn(sourceObjects[y], sourceObjects[x]))
continue ;
int minIndex = x + 1;
int maxIndex = y + 1;
QLink[maxIndex]++;
Nodes[minIndex] = new Node(maxIndex, Nodes[minIndex]);
}
}
}
protected internal int FindNonRelatedNodeIndex() {
int r = 0;
int n = SourceObjects.Count;
for ( int i = 0; i <= n; i++) {
if (QLink[i] == 0) {
QLink[r] = i;
r = i;
}
}
return r;
}
protected virtual IList<T> ProcessNodes( int r) {
int n = sourceObjects.Count;
int k = n;
int f = QLink[0];
List <T> result = new List <T>(n);
while (f > 0) {
result.Add(sourceObjects[f - 1]);
k--;
Node node = Nodes[f];
while (node != null ) {
node = RemoveRelation(node, ref r);
}
f = QLink[f];
}
return result;
}
Node RemoveRelation(Node node, ref int r) {
int suc_p = node.RefCount;
QLink[suc_p]--;
if (QLink[suc_p] == 0) {
QLink[r] = suc_p;
r = suc_p;
}
return node.Next;
}
}
#endregion
* This source code was highlighted with Source Code Highlighter .
結論
必要に応じて、相互に依存するオブジェクトを処理する特定の順序で、トポロジカルソートアルゴリズムを使用してオブジェクトを事前に順序付けできます。 その結果、オブジェクトの正しいシーケンスとそれらに対するアクションの実行が構築されます。
この記事で提案されているアルゴリズムには、次の利点があります。
- 一般化(汎用)の使用、つまり さまざまなタイプのオブジェクトをソートするために使用できます
- 独自のComparerクラスを定義する機能。つまり、オブジェクトを比較するためのさまざまなロジックを実装できます。
- アルゴリズムの線形性、アルゴリズムは再帰的ではありません
ソースコードの例は
ここで利用可能
です 。
この資料が将来のプロジェクトで役立つことを願っています。