再帰的なzipアーカイブ

多くのHabraユーザーは、おそらくquains-独自のソースコードを表示するプログラムに精通しています。 今日は、面白いバージョンのquineを作成する方法を示したい- それ自体に解凍されたZIPアーカイブ。

Lempel-Zivアルゴリズム

ZIPファイル（ Lempel-Ziv ）で使用されるアルゴリズムは、実際には非常に単純です。 命令には2種類あります。 literal(n)後にそのまま出力する必要があるデータストリームと、 dバイト戻り、この位置からnバイトを出力するrepeat(d, n)です。

したがって、タスクは次のとおりです。このアルゴリズムを使用して、起動時にコードを表示するプログラムを作成します。 つまり、それ自体に展開する圧縮データストリームを記述します。 最大プログラム：最初と最後に任意のデータを使用してそれ自体に拡張するストリームを作成します（ヘッダーと他の必要なデータを含む実際のzipまたはgzipファイルとして使用できるように）。

LnとRnをliteral(n)とrepeat(n, n)省略形として使用することに同意しましょう。プログラムは各コードが1バイトであると想定します。 L0はそれぞれ、Lempel-ZivのNOPの類似体であり、 L5 helloはL5 helloを出力します。 同じことがL3 hel R1 L1 oを推定します。

簡単なクインは次のようになります。

		コード		おわりに
ノーオペレーション		L0
ノーオペレーション		L0
ノーオペレーション		L0
4バイトを印刷		L4 L0 L0 L0 L4		L0 L0 L0 L4
最後の4バイトを繰り返します		R4		L0 L0 L0 L4
4バイトを印刷		L4 R4 L4 R4 L4		R4 L4 R4 L4
最後の4バイトを繰り返す		R4		R4 L4 R4 L4
4バイトを印刷		L4 L0 L0 L0 L0		L0 L0 L0 L0

（「コード」列と「出力」列の内容は同じであることがわかります）

プログラムの興味深い部分は、6バイトのシーケンスL4 R4 L4 R4 L4 R4であり、8バイトを出力します： R4 L4 R4 L4 R4 L4 R4 。 つまり、1バイト前と1バイト後に自分自身を表示します。

Pythonでquineを作成する場合、通常、問題はprintステートメントがprintものよりも常に長いことです。 この問題を再帰的に解決し、行を印刷自体に置き換えます。 ここでは、別のアプローチを使用できます。 Lempel-Zivのプログラムは部分的に繰り返されるため、繰り返される部分文字列には元のフラグメント全体が含まれます。 ここでの再帰とは、プログラムの実行そのものではなく、プログラムの表示そのものです。 いずれにせよ、このフラグメントは重要です。 最終的なR4まで、プログラムの出力は入力よりも遅れます。 実行後、出力は入力の1バイト先になります。

ダミー演算子L0は、プログラムのより一般的なバージョンでも使用できます。これは、任意の3バイトのプレフィックスとサフィックスでそれ自体を補完できます。

		コード		おわりに
4バイトを印刷		L4 aa bb cc L4		aa bb cc L4
最後の4バイトを繰り返します		R4		aa bb cc L4
4バイトを印刷		L4 R4 L4 R4 L4		R4 L4 R4 L4
最後の4バイトを繰り返す		R4		R4 L4 R4 L4
4バイトを印刷		L4 R4 xx yy zz		R4 xx yy zz
最後の4バイトを繰り返す		R4		R4 xx yy zz

（出力は、コードに加えてaa bb ccが先頭に追加され、 xx yy zzが末尾に追加されます）

この時点に到達するために日曜日のほとんどを費やさなければなりませんでしたが、それをしたとき、私はすでに勝ったことをすでに知っていました。 私の実験から、いくつかの指示なしに自分自身を表示するプログラム、またはいくつかの指示を除いたプレフィックス付きで自分自身を表示するプログラムを作成することは非常に簡単であることがわかりました。 出力の追加バイトaa bb ccを使用すると、プログラムに目的のフラグメントを追加できます。 また、自分自身を出力するコードと、余分な3バイトxx yy zzを出力するコードを書くのも簡単です。 これら2つのトリックを使用して、ヘッダーと追加データを最後にアーカイブに追加できます。

これは、任意のプレフィックスとサフィックスを持つプログラムがどのように見えるかです：

		コード		おわりに
印刷プレフィックス		[P]		P
p + 1バイトを出力		L p +1 [P] L p +1		[P] L p +1
最後の p +1バイトを 繰り返す		R p +1		[P] L p +1
1バイトを印刷		L1 R p +1		R p +1
1バイトを印刷		L1 L1		L1
4バイトを印刷		L4 R p +1 L1 L1 L4		R p +1 L1 L1 L4
最後の4バイトを繰り返します		R4		R p +1 L1 L1 L4
4バイトを印刷		L4 R4 L4 R4 L4		R4 L4 R4 L4
最後の4バイトを繰り返します		R4		R4 L4 R4 L4
4バイトを印刷		L4 R4 L0 L0 L s +1		R4 L0 L0 L s +1
最後の4バイトを繰り返します		R4		R4 L0 L0 L s +1
ノーオペレーション		L0
ノーオペレーション		L0
出力 s +1バイト		L s +1 R s +1 [S]		R s +1 [S]
最後のs +1バイトを 繰り返す		R s +1		R s +1 [S]
印刷接尾辞		[S]		S

（出力はP、次に「コード」列のバイト、次にSです。）

解凍されたzipファイル

次に、実際のアクションに進みます。 再帰的なZIPファイルを作成するという主要な技術的問題を解決しましたが、さらにいくつかの詳細が残っています。

最初の問題：簡略化されたオペコードに記録されたクインを実際のLempel-Zivオペコードに変換します。 RFC 1951は、gzipおよびzipで使用されるDEFLATE形式を定義しています。 ハフマンコーディングによってエンコードされた一連のオペコードを含むブロックのシーケンス。 ハフマンコーディングは、異なる長さの文字列を異なるオペコードに割り当てます。これは、オペコードが同じ長さであるという仮定と一致しません。 しかし、ちょっと待ってください！ 試してみると、使用できる固定長エンコードを見つけることができます。

DEFLATEにはリテラルブロックとオペコードブロックがあります。 リテラルブロックヘッダーは5バイトです。



オペコードLがそれぞれ5バイトを占有する場合、オペコードRも5バイトを占有し、上記の各バイトは5回繰り返されます（たとえば、L4の引数は20バイトになり、R4は出力の最後の20バイトを繰り返します）。 1回のrepeat(20,20)を持つオペコードのブロックは、5バイトよりわずかに少なくなります。



幸いなことに、2つのrepeat(20,10)命令を含むオペコードブロックでも同じことが行われ、正確に5バイトかかります。



異なる引数の長さでrepeatをエンコードするには、さらに複雑なトリックが必要ですが、9〜64バイトの長さの文字列を繰り返す5バイトコードを開発できるようです。 たとえば、10バイトと40バイトを繰り返すブロックを次に示します。





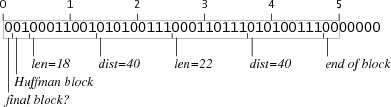
最後の10バイトを繰り返すブロックは必要なものより2ビット少なくなりますが、各繰り返しブロックの後には3つのゼロビットで始まり、最も近いバイトの境界まで完了するリテラルのブロックが続きます。 繰り返しブロックが境界の2ビット前で終了し、その後にリテラルのブロックが続く場合、パディングは欠落している2ビットを挿入します。 同様に、40バイトを繰り返すブロックは5ビットで海外に行きますが、これらのビットはゼロです。 5ビット後にブロックを開始し、これらのビットを仕上げから取り除きます。 繰り返しブロックの最後の7ビットがゼロであり、リテラルブロックの最初のバイトのビットもゼロであるため、これらのトリックは両方とも機能します。したがって、境界線は表示されません。 リテラルのブロックが1ビットで始まる場合、このトリッキーなトリックは機能しません。

2番目のハードルは、zipアーカイブ（およびgzipも）が非圧縮データのチェックサムを保存することです。 非圧縮データは同じzipアーカイブであるため、チェックサムも計算に関与します。 したがって、チェックサムがxと等しくなるxの値を見つける必要があります。 再帰が逆行します。

CRC32コマンドは、ファイル全体を1つの大きな数値として解釈し、特別な除算方法を使用してこの数値を特定の定数で除算するときに剰余を計算します。 対応する方程式を記述してxについて解くことができますが、今日は十分な再帰パズルがあります。 x 40億を超える有効な値があり、直接列挙することで必要なものを非常によく見つけることができます。

これをすべて自分で繰り返したい場合、たとえば、tarファイルを512で割って残りを残さず、zipヘッダーを59バイトに圧縮してRs+1 R64以下になるなど、いくつかの簡単な問題Rs+1あります。 しかし、これはプログラミングの問題です。

そこで、 r.gz （gzipアーカイブ）、 r.tar.gz （tarファイル、圧縮gzip）、およびr.zip （zipアーカイブ）のファイルを入手しました。 残念ですが、これらのファイルを無期限に再帰的に解凍するプログラムは見つかりませんでした。 見るのは楽しいでしょうが、それほど洗練されていないジップボムはすでに私たちを楽しませています。

適切な場合は、これらのファイルを生成するGoプログラムrgzip.goがあります。 gzipファイルを含むzipファイルを作成できますか。gzipファイルには、元のzipファイルが含まれます）。 ケン・トンプソンは、少し大きいサイズのコピーを解凍するzipアーカイブを作成することを提案しました。そのため、再帰的に解凍すると、アーカイブのサイズは無限に大きくなります（どちらかで成功した場合はコメントを残してください）。