LogLog-一意の要素の数を見つける

こんにちは、Habr！ あなたと私はすでにブルームとMinHashフィルターにふけっています。 今日は、最小限のメモリオーバーヘッドで大量のデータ内の一意の要素のおおよその数を決定できる、別の確率的ランダム化アルゴリズムについて説明します。

まず、タスクを設定しましょう：大量のテキストデータ（たとえば、悪名高いシェークスピアの文学作品の成果）があり、このボリュームで見つかったさまざまな単語の数を計算する必要があるとします。 典型的な解決策は、ハッシュテーブルが切り捨てられたカウンターです。この場合、キーは値が関連付けられていない単語になります。

この方法は誰にとっても良いことですが、作業には比較的大量のメモリが必要ですが、ご存知のように、私たちは落ち着きのない効率の天才です。 十分ではないにせよ、多くの理由-上記のシェークスピアの語彙のおおよそのサイズは、128バイトのメモリを使用して計算できます。

アイデア

いつものように、何らかのハッシュ関数が必要です;したがって、データ自体ではなく、それらのハッシュがアルゴリズムの入力になります。 ハッシュ関数のタスクは、通常ランダム化アルゴリズムの場合と同様に、順序付けられたデータを「ランダム」データに変換することです。つまり、定義ドメインが値のドメイン全体にほぼ均一に広がります。 テスト実装では、 FNV-1aを単純で簡単なハッシュ関数として選択しました。

function fnv1a(text) { var hash = 2166136261; for (var i = 0; i < text.length; ++i) { hash ^= text.charCodeAt(i); hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24); } return hash >>> 0; } 

さて、脳をオンにして、それがバイナリ表現で与えるハッシュを見てください：

fnv1a('aardvark') = 1001100000000001110100100011001 1
fnv1a('abyssinian') = 00101111000100001010001000111 100
fnv1a('accelerator') = 10111011100010100010110001010 100
fnv1a('accordion') = 0111010111000100111010000001100 1
fnv1a('account') = 00101001010011111100011101011 100
fnv1a('accountant') = 0010101001101111110011110010110 1
fnv1a('acknowledgment') = 0000101000010011100000111110 1000
fnv1a('acoustic') = 111100111010111111100101011000 10
fnv1a('acrylic') = 1101001001110011011101011101 1000
fnv1a('act') = 0010110101001010010001011000101 1

各ハッシュの最初の非ゼロの下位ビットのインデックスに注意を払い、このインデックスに1を追加してランク（rank（1）= 1、rank（10）= 2、...）と呼びましょう：

 function rank(hash) { var r = 1; while ((hash & 1) == 0 && r <= 32) { ++r; hash >>>= 1; } return r; } 

ランク1のハッシュを持つ確率は0.5、ランク2-0.25、ランクr -2 ^{- r}です。 つまり、2 ^r個のハッシュのうち、ランクrの 1つのハッシュが満たされる必要があります。 言い換えれば、検出された最大のRランクを覚えていれば、2 ^Rは既に表示されている要素の中で一意の要素の数の大まかな推定値として適合します。

確率論は、小さなサンプルで大きなランクRを見つけることができる、または巨大なサンプルで小さなランクRを見つけることができるようなものであり、一般に2 ³¹と2 ³²は2つの大きな違いです、あなたは言う、あなたは正しい、だからそのような単一の推定とても失礼です。 どうする？

1つのハッシュ関数の代わりに、これらのバンドルを使用して、それらのそれぞれについて取得した推定値を何らかの方法で「平均化」できます。 多くの関数が必要であり、それらすべてを考慮する必要があるため、このアプローチは不適切です。 したがって、次のトリックを行います。各ハッシュのk個の最上位ビットを削除し、これらのビットの値をインデックスとして使用して、1つの推定値ではなく2 ^k個の評価の配列を計算し、それらに基づいて整数値を取得します。

HyperLogLog

実際、LogLogアルゴリズムにはいくつかのバリエーションがありますが、比較的最近のオプションであるHyperLogLogを検討します。 このバージョンでは、標準エラー値を達成できます。

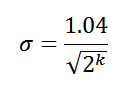
したがって、上位8ビットをインデックスとして使用すると、一意の要素の真数の標準誤差6.5％（ σ = 0.065）が得られます。 そして最も重要なことは、 気違いの スキルに確率論を装備すれば、次の最終評価に到達できることです。

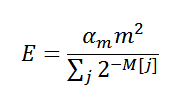
ここで、 αmは補正係数、 mは評価の総数（2 ^k ）、 Mは推定自体の配列です。 これでほとんどすべてがわかったので、 実装の時間です：

 var pow_2_32 = 0xFFFFFFFF + 1; function HyperLogLog(std_error) { function log2(x) { return Math.log(x) / Math.LN2; } function rank(hash, max) { var r = 1; while ((hash & 1) == 0 && r <= max) { ++r; hash >>>= 1; } return r; } var m = 1.04 / std_error; var k = Math.ceil(log2(m * m)), k_comp = 32 - k; m = Math.pow(2, k); var alpha_m = m == 16 ? 0.673 : m == 32 ? 0.697 : m == 64 ? 0.709 : 0.7213 / (1 + 1.079 / m); var M = []; for (var i = 0; i < m; ++i) M[i] = 0; function count(hash) { if (hash !== undefined) { var j = hash >>> k_comp; M[j] = Math.max(M[j], rank(hash, k_comp)); } else { var c = 0.0; for (var i = 0; i < m; ++i) c += 1 / Math.pow(2, M[i]); var E = alpha_m * m * m / c; // -- make corrections if (E <= 5/2 * m) { var V = 0; for (var i = 0; i < m; ++i) if (M[i] == 0) ++V; if (V > 0) E = m * Math.log(m / V); } else if (E > 1/30 * pow_2_32) E = -pow_2_32 * Math.log(1 - E / pow_2_32); // -- return E; } } return {count: count}; } function fnv1a(text) { var hash = 2166136261; for (var i = 0; i < text.length; ++i) { hash ^= text.charCodeAt(i); hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24); } return hash >>> 0; } var words = ['aardvark', 'abyssinian', ..., 'zoology']; // 2 336 words var seed = Math.floor(Math.random() * pow_2_32); // make more fun var log_log = HyperLogLog(0.065); for (var i = 0; i < words.length; ++i) log_log.count(fnv1a(words[i]) ^ seed); var count = log_log.count(); alert(count + ', error ' + (count - words.length) / (words.length / 100.0) + '%'); 

使用しているメモリのバイト数を見積もってみましょう。kは8です。したがって、配列Mは256要素で構成され、各要素は条件付きで4バイト（合計1 KB）を取ります。 悪くはないが、もっと少なくしたい。 考えてみると、配列Mからの1つの推定のサイズを小さくすることができます-ceil（log2（32 + 1- k ））ビットが必要です。k = 8の場合は5ビットです。 合計で160バイトありますが、これはすでにはるかに優れていますが、さらに少なくすることを約束しました。

少なくするためには、データ内の一意の要素の最大可能数-Nを事前に知る必要があります。 確かに、それを知っていれば、ハッシュから可能なすべてのビットを使用してランクを決定する必要はなく、ceil（log2（ N / m ））ビットで十分です。 この数から、配列Mの 1つの要素のサイズを取得するために対数を取る必要があることを忘れないでください。

単語の小さなセットの場合、それらの最大数が3,000であると仮定すると、64バイトしか必要ありません。 シェークスピアの場合、 Nを100,000に設定します。約束の128バイトにエラーが6.5％、192バイトに4.6％、768に3.3％のエラーがあります。 ところで、シェークスピアの語彙の実際のサイズは約30,000語です。

その他の考え

もちろん、たとえば各3ビットの小さな「バイト」を使用しても、パフォーマンスの点ではあまり効率的ではありません。 実際には、ビット操作の非常に長いチェーンを構築するのではなく、アーキテクチャ固有の通常のバイトを使用する方が賢明です。 それでも「挽く」ことに決めた場合は、評価を修正するコードを修正することを忘れないでください。

小さなスプーン1杯のタール、エラーσは最大エラーではなく、いわゆる標準エラーです。 私たちにとって、これは結果の65％がσ以下 、95％ -2σ以下 、99％ -3σ以下の誤差を持つことを意味します。 まったく問題ありませんが、予想よりも大きなエラーを含む回答が得られる可能性が常にあります。

私の実験から判断すると、特にデータがほとんどない場合は、その削減に夢中になってはいけません。 この場合、修正手順が開始されますが、これは常にその責任に対処するとは限りません。 もちろん、これが私の実装での愚かな間違いでない限り、アルゴリズムは特定のタスクのテストとチューニングを必要とするようです。 これは完全に真実ではありません 。

32ビット幅のハッシュ関数を使用する場合、アルゴリズムにより、達成可能な最小の標準誤差約0.5％で最大10 ^9個の一意の要素を計算できます。 このようなエラーが発生したメモリには、約32〜64 Kバイトが必要です。 一般に、LogLogは、ライブデータストリームのオンライン作業に最適です。

それだけです さようなら！