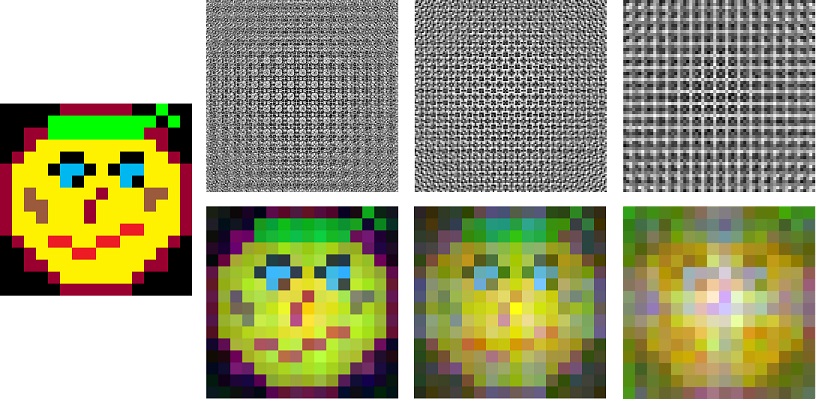
 ホログラムの
ホログラムの驚くべき特性の1つに驚いたとき、オブジェクトのホログラフィックイメージをフラグメントに分割することで、各フラグメントからオブジェクト全体のイメージを復元できますが、品質はわずかに低下します。 同志の
eresik によるトピック
「情報のホログラフィックコーディングとデコーディングの実験」を読んだ後
、私は確かにそのようなデジタルホログラムを自分で実装したいと考えました。 そのアルゴリズムに基づいて、Delphiを起動し、動作するように設定しました。 最後に、オッズで少し整頓したので、
eresikが受け取ったものに似た適切な白黒の絵を手に入れ始めました。 ホログラムの一部を消去すると、驚くべきことに、元の画像が復元されました! それで、これはどうして起こるのでしょうか? 物理学や数学に入らずに、ホログラムのこの特性を明確に説明できる方法を説明しようと思います。
元のオブジェクトを考えます。これは、単一の白いドットとその横に取得されたホログラムを含む画像です。


ご覧のとおり、結果のホログラムは、この点から発散する波です。 そして、これらの波からのソース画像が存在しない場合、これらの波のソースの位置、つまり白色点を復元できます。
再構成されたホログラム画像の結果:

はい...そして、例えば、白ではなく、灰色の点(より低い輝度)をとると、それに応じて、灰色のみの同じ波(より低い強度)を受け取ります。 つまり ホログラムによって、ポイントの位置だけでなく、明るさも復元できます。 次に、既存のホログラムの約半分を分割します。 残りをよく見てください:

この部分からでも、波がどこから発散するかを理解でき、それに応じて開始点の位置を決定できることが明らかになります。
ホログラムの断片から復元された画像:

さらに、ホログラムをそれぞれの小さな部分に分割すると、波の完全な構成に関する情報が次第に少なくなり、開始点を正確に特定することがますます困難になります。
次に、最初の1つである2点の画像を取得して、ホログラムを作成します。 この場合、ホログラム上で、ある点と別の点から発散する波を観察します。 これらの波は重なり合い、全体像はこれらの波の合計になります。

この図から、ポイントの位置を簡単に決定することもできます。 繰り返しますが、ホログラムの特定の部分を分割し、残りのフラグメントから、ポイントがほぼどこにあるかを再び判断することができます。


したがって、各ホログラムポイントはある程度、オブジェクト全体に関する情報を含みます。
元の画像にドットを追加すると、より複雑な干渉パターンが表示されます。 視覚的には、元の画像のタイプ、たとえばそのようなホログラムを判別することはすでに非常に困難です。

ただし、この品質の元の画像を復元するのに十分な情報が含まれています。

この場合、再構成された画像は1つまたは2つのポイントの場合よりもノイズが多くなり、元の画像として少数のコントラストポイント以外を使用することはほとんど不可能であることがわかります。
eresikが書いたように、
大きな音
には2つの理由
があります。 1つ目は、ポイントの輝度が0..255の範囲の整数に丸められることです。 しかし、実験中に判明したように、この要素は決定的な役割を果たしていません。 ノイズレベルは、主に写真プレートの解像度によって決まります。 上記の画像では、元の16x16画像の解像度と256x256ピクセルの写真プレートを使用しましたが、これは悪くはありませんが、わかりやすくするために波長Wを大きすぎる= 2に選択しました。 より短い波長W = 0.1を選択すると、ノイズレベルを大幅に低減できます。
W = 0.1での元のホログラムと再構成画像:
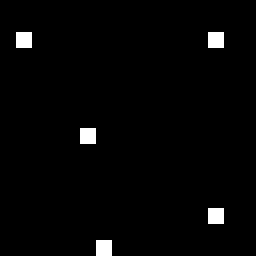


しかし、写真プレートの最終解像度には、最小波長に制限があり、それを超えると強いノイズが現れ始めます。
W = 0.003のホログラムと再構成画像:


カラー画像処理を追加することで、同志の
eresikのアルゴリズムを
少し改善しました。 写真プレートで実際のホログラムを受け取るように、赤、緑、青の光に対応する3つの異なる長さの波の干渉が露出します。 また、ホログラムの解像度は元の画像の解像度と異なる場合があります。
トピックの最初に、写真プレート192x192、128x128、64x64および波長WR = 0.03から16x16カラー画像を復元する例を見ることができます。 WG = 0.029; WB = 0.028。 以下は、同じパラメーターを使用して192x192の写真プレートの元の32x32画像を復元する場合です。

したがって、選択した解像度に応じて、異なる品質の画像をデコードするときに取得できることがわかります。
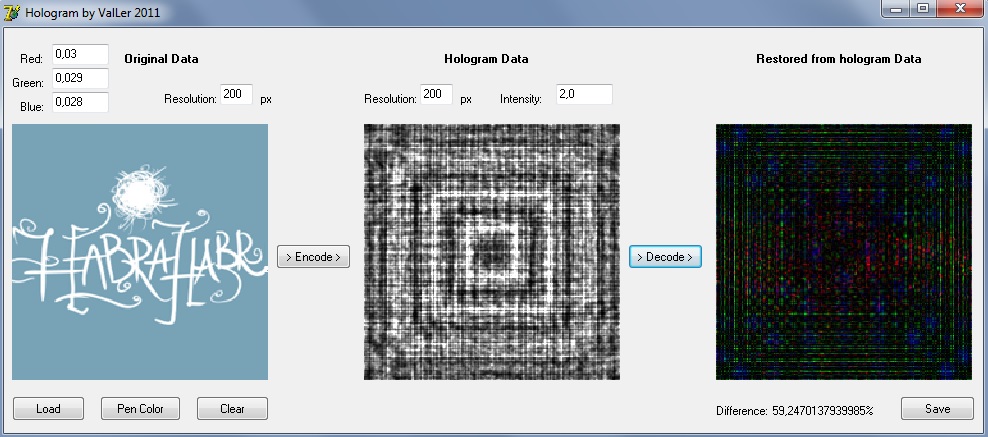
そして、最後に、プログラムを実際に試してみたり、さまざまな入力データを使用したり、解像度や波長を変更したりできます。 このプログラムでは、bmpファイルをソースイメージとしてダウンロードし、それらに変更を加え、ホログラムを上書き/ノイズ処理し、復元されたイメージとピクセルの輝度に基づいて元のイメージとの差異の程度を計算できます。 100%の違いは、再構成された画像が元の画像に対して反転していることを意味します。
Habrのトランスコードに失敗したプログラムの画面:
 プログラムソースコード
プログラムソースコード