多くの人は、
Magic Square (MK)の概念を知っています-1 x N ^ 2の自然数で満たされた正方形のテーブルN x Nで、各行、対角線、および列の数値の合計は... N *(N ^ 2 + 1)/ 2。
学校では、数学に興味があり、Nが奇数のMKの興味深い性質に気づきました。もちろん、これらの性質はすでに知られているかもしれませんが、私はそれを詳しく調べませんでした、そしてそれがどこで誰に役立つかについてもわからない、私はかつて驚いたと述べています。
したがって、ビット深度MK、たとえばN = 7があります。
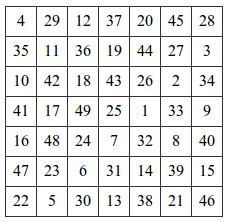
このMKで2の倍数であるすべての数値を見つけて、赤いマーカーでマークすると、画像が得られます。

同様に、3の倍数:
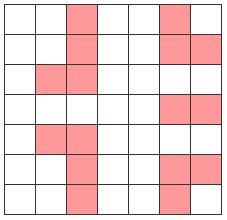
... 5の倍数:

... 7の倍数:
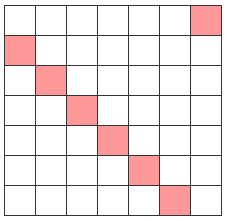
明確なパターンがすぐに明らかになります。 他の奇数次元Nについても、同様の規則性が得られます。