ポスト
ミルズモデルへの継続。
ペア評価
このモデルでは、2人の専門家(または専門家グループ)がプログラムをテストする必要があります。 ただし、プログラムに人為的なエラーを導入する必要はありません。 そのため、2つの専門家グループがプログラムを個別にテストできるようにします。 プログラムにN個のエラーが含まれているとします。 最初のグループでN
1個のエラーを見つけ、2番目のグループでN
2個のエラーを見つけます。 両方のグループでいくつかのエラーが検出されました。 N
12個のそのようなエラーがあるとします。

グループが発見したエラーの割合を通じて、グループの作業の有効性を評価します。
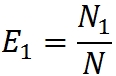
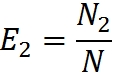
すべてのエラーを見つける可能性は等しくあります(私の意見では、ミルの場合のように、このモデルの信頼性が低下します)。 次に、エラーを見つける確率が等しいため、ランダムに選択されたNのサブセットはセットN全体の近似と見なすことができます。つまり、最初のグループがすべてのエラーの10%を検出した場合、ランダムに選択されたサブセットの約10% 。
そのようなランダムに選択されたサブセットとして、2番目のグループで見つかったエラーのセットを使用します。 最初のグループで見つかったすべてのエラーの割合はN
1 / Nです。 2番目のグループで見つかったエラーのうち、最初のグループで見つかったエラーの割合はN
12 / N
2です。 この推論によると、これらの2つの量は等しいはずです。
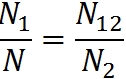
したがって、プログラム内のエラーの数:

見つかったエラーの数は(NN
1 -N
2 + N
12 )です。
たとえば、最初のグループで8つのエラーを検出し、2番目のグループで9つのエラーを検出します。両方のグループで3つのエラーを検出しました。 次に、プログラムのエラー数はN =(8 * 9/3)= 24です。 これらのうち、すでに見つかった(8 + 9-3)= 14。 したがって、10個を見つけることが残っています。
歴史的経験
このモデルは、IBMが
OS / 360で作業する過程で登場しました。 エラー数の推定には、次の式が使用されました。N= 2 * IM + 23 * MIM。 ここに
Nはエラーによる修正の総数です。
IM-修正可能なモジュールの数、
MIM-繰り返し修正されたモジュールの数。
複数の修正可能なモジュールは、10以上の修正が必要なモジュールと見なされました。 MIは、新しいモジュールの90%、古いモジュールの15%と評価されました。 MIM-新規15%、旧6%。 このような推定値を式に代入すると、次の形式が得られます。
N
fix = 2 *(0.9 * N
新しいmod。 + 0.15 * N
古いmod。 )+ 23 *(0.15 * N
新しいmod。 + 0.06 * N
古いmod。 )
したがって、システムに140のモジュールがあり、更新プロセスでさらに20を追加する必要がある場合、この場合に検出されるエラーの数は次のように推定されます。
2 *(0.9 * 20 + 0.15 * 140)+ 21 *(0.15 * 20 + 0.06 * 140)= 2 *(18 + 21)+ 23 *(3 + 8.4)= 78 + 262.2 = 340.2
340個のエラーが予想されます。 20の新しいモジュールのうち18で、少なくとも1つの修正を行う必要があります。3つのモジュールでは、少なくとも1ダースです。 古いモジュールのうち、少なくとも1回は21個のモジュール、8個または9個のモジュールを修正する必要があります(少なくとも10回)。
このようなモデルは特定のシステム用に開発されたことを念頭に置いてください。 他の場合に直接適用できるという事実ではありません。
記事を書く際に、私たちは「ダミー」だけでなく「ダミー」のテストとデバッグのマニュアルを使用しました(MA Plaksin)