NetworkXライブラリは、複雑なネットワーク構造の構造、ダイナミクス、機能を作成、操作、研究するために検討されています。
ライブラリを学習ツール、応用プログラミング、または研究として使用する基本を考慮します。
ライブラリの説明の基礎は、サイトの公式資料です。
ライブラリ1.5のバージョンが考慮されます。

ライブラリ機能

networkXライブラリはPythonで作成され、グラフやその他のネットワーク構造で動作するように設計されています。これは、新しいBSDライセンスの下で配布されるフリーソフトウェアです。
ライブラリの主な機能：

単純な、指向性のある、重み付けされたグラフを操作するためのクラス。
ノードは、時系列、テキスト、画像、XMLなど、ほとんど何でもかまいません。
最も一般的なグラフストレージファイル形式への/からのグラフの保存/読み込み。
基本的なタイプのグラフを作成するための組み込み手順。
サブグラフ、クリック、およびK-partite graphs（K-core）（各頂点が少なくともレベルKを持つ最大サブグラフ）を検出する方法。
頂点の角度、グラフの高さ、直径、半径、経路の長さ、中心、中間性などのグラフの特性を取得する
ネットワークを2Dおよび3Dグラフの形式で視覚化します。
その他多数...

性能

ライブラリは、非常に大規模なネットワーク構造、1000万のノードとそれらの間に1億のアークがあるグラフレベルで自由に動作することが述べられています。「辞書辞書」と呼ばれるPython言語の低レベルのデータ構造に基づいているため、メモリは効率的に使用され、グラフは適切にスケーリングされ、スクリプトが実行されるオペレーティングシステムの機能にほとんど依存せず、現在人気のある分析領域に優れていますソーシャルネットワークとグラフからのデータ。

基本的なデータ構造

ライブラリは、パッケージの階層として編成されています。各パッケージの上位レベルは、その構造を操作するための一般的な方法を提供し、下位パッケージはより多くの専門性を獲得します。
以下のすべての例では、networkXは次のディレクティブに接続されています。

>>> import networkx as nx

クラスグラフ

次の主要なタイプのグラフがサポートされています。

グラフは、単純な無向グラフの実装です。 2つのノード間の追加の頂点は無視され、自身に接続されたノードは可能です。
DiGraphは有向グラフであり、このタイプのグラフに固有の機能と制限が追加されています。
MultiGraph-マルチグラフの実装。このようなグラフグラフには、複数のエッジ（非方向性）、または反対方向の2つ以上の円弧で接続された頂点のペアが存在する場合があります。
MultiDiGraphは、適切な向きのマルチグラフです。

さまざまなタイプの空のグラフを作成する例：

 >>> G=nx.Graph() >>> G=nx.DiGraph() >>> G=nx.MultiGraph() >>> G=nx.MultiDiGraph()

グラフの内部表現は、隣接リストとして実装されます。ただし、矛盾を回避するために、グラフを使用したすべての操作は、このリストではなく、ライブラリ関数APIを使用して直接実行する必要があります。

ノットとアーク

グラフのコンポーネント。すべてのノードまたはアークには、それに関連付けられたすべての情報を取得できる一意の識別子があり、さらに、このデータを取得できる識別子よりも現在のアルゴリズムを実装するのに便利な名前がある場合があります。
さらに、各ノードまたはアークは、さまざまなタイプのデータを格納する属性をいくつでも持つことができます。重み付きグラフには「重み」と呼ばれるサービス属性があり、この名前を使用して他の情報を保存して、その表現の内部ロジックの破壊を回避することはできません。

グラフ作成

現時点では、次の3つの方法のいずれかを使用してグラフを作成できます。

1.グラフジェネレータ-さまざまなレベルの完全なグラフ、バランスツリー、巡回グラフ、ドロゴフツェフゴルツェフメンデスグラフ、ランダム二項グラフなど、一般的なトポロジのグラフを作成するための定義済みクラス。詳細については、ドキュメントを参照してください： networkx.lanl.gov/reference/generators.html
2.サポートされている形式のいずれかのファイルまたはデータストリームに基づくデータの読み込みとグラフの生成：
3.ノードとアークの順次追加。

作成されたグラフには、一般的なメソッドとメソッド固有のメソッドの両方があります。

 >>> import networkx as nx >>> G=nx.Graph() >>> G.add_edge(1,2) #       = 1 >>> G.add_edge(2,3,weight=0.9) #

追加された値はさまざまなタイプのデータを提供できるため：

 >>> import math >>> G.add_edge('y','x',function=math.cos) >>> G.add_node(math.cos) #    hashable

配列とデータ値からアークを追加することもできます。

 >>> elist=[('a','b',5.0),('b','c',3.0),('a','c',1.0),('c','d',7.3)] >>> G.add_weighted_edges_from(elist)

グラフ情報を取得する

グラフの作成に加えて、通常、ノード、アーク、パスなどに関する情報を取得する必要があります。このための主な方法は、ノードとアークの配列（それぞれ、エッジ（）とノード（））を取得することです。およびnodes_iter（））。
さらに、グラフに関するより具体的な情報を取得するための多数の関数があります。たとえば、nx.triangles（G、n）は、頂点nがノードの1つであるグラフGの三角形の数を返します。
利用可能なすべての機能は、 networkx.lanl.gov/reference/algorithmsのドキュメントセクションで説明されています。

定義済みのアルゴリズム

このライブラリは、グラフでの作業に典型的な多数のアルゴリズムを実装しています。最短経路の検索、高さと幅の検索、クラスタリング、グラフの同型の検索などのアルゴリズムが実装されています。
たとえば、重み付きグラフ上の最小パスを見つけるためのダイクストラのアルゴリズムは、次のように実装されます。

 >>> G=nx.Graph() >>> e=[('a','b',0.3),('b','c',0.9),('a','c',0.5),('c','d',1.2)] >>> G.add_weighted_edges_from(e) >>> print(nx.dijkstra_path(G,'a','d')) ['a', 'c', 'd']

グラフの視覚化

ライブラリの主な目的はグラフを操作することであり、視覚的な表示は二次的ですが、重要な分析ツールであるため実装されます。
Matplotlib Pythonライブラリまたはより複雑なケースのGraphvizプラグインを使用してグラフを表示するための便利なメソッドが提供されています。視覚化機能に関する完全なドキュメントはnetworkx.lanl.gov/reference/drawing.htmlで入手できます。
簡単なグラフの視覚化の例：

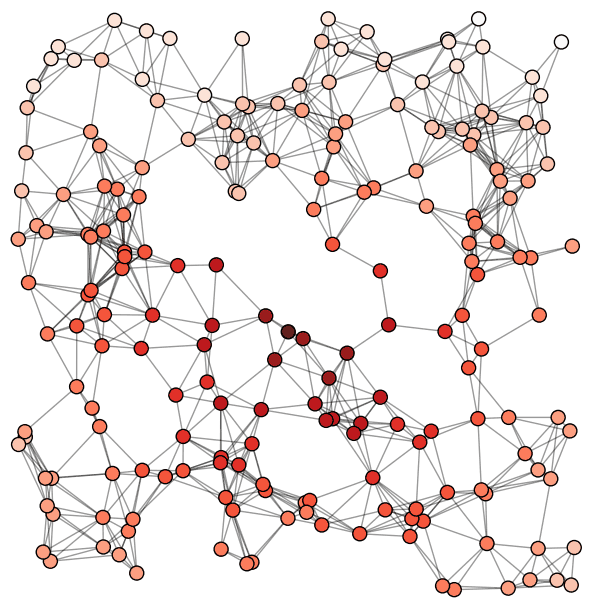
 >>> G=nx.cubical_graph() >>> nx.draw(G) #    spring_layout >>> nx.draw(G,pos=nx.spectral_layout(G), nodecolor='r',edge_color='b')

Matplotlibを使用した可視化

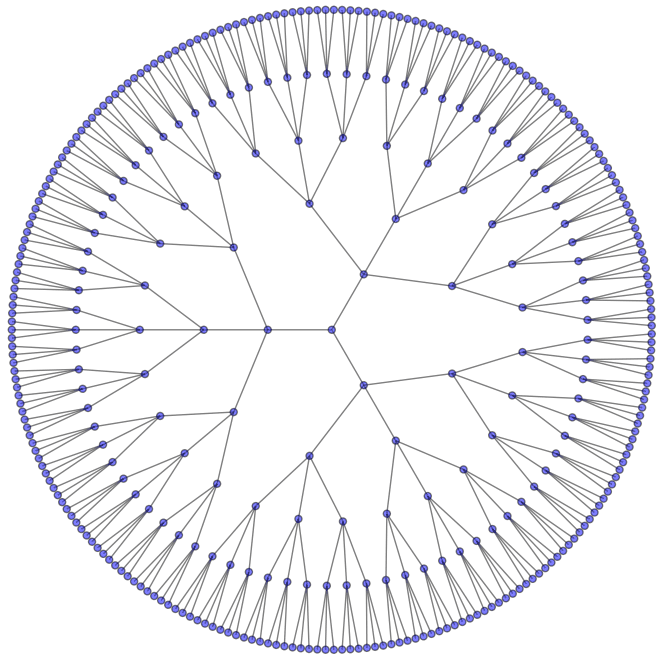
Graphvizを使用した可視化
巡回グラフとして表される完全なツリー

データ構造

グラフの内部表現全体は、辞書の辞書をメインデータタイプとして使用します。このアプローチには多くの利点があります。たとえば、多次元配列の要素へのアクセスの表記法を使用したノードへの便利なアクセス：

 >>> G=nx.Graph() >>> G.add_edge(1,2,color='red',weight=0.84,size=300) >>> print(G[1][2]['size']) 300

より詳細なドキュメントは、 http：//networkx.lanl.gov/reference/indexにあります。 html
このライブラリでの作業は本当に楽しかったです。いくつかの小さなスクリプトを使用しましたが、1つの小さな研究でそれをうまく実装したいと思っています。
成功したプロジェクト！

NetworkXにより、ネットワーク構造を使用した便利な作業が可能