DJIインデックスの増分が統計的に独立しているかどうかの仮説をテストしてみましょう。 この場合、比較する参照データソースとして、元の系列の実際の増分から生成された人工的な時系列を使用しますが、同時にランダムに混合します。 統計的な独立性の尺度として、相互情報の統計を使用します。
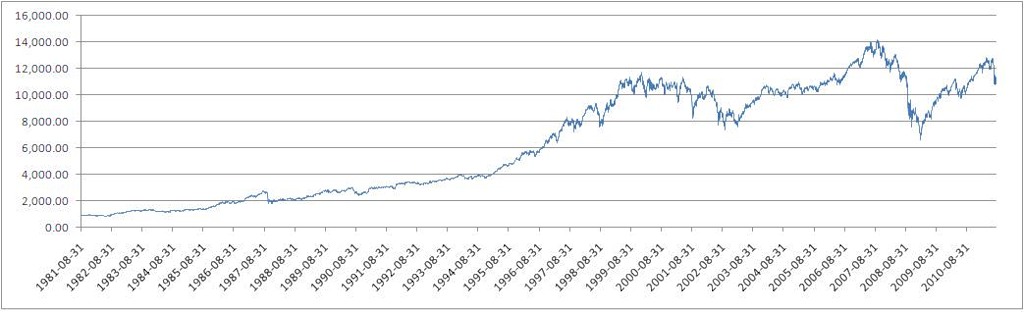
実験データソースとして、1981年8月31日から2011年8月26日までの30年間(毎日の終値)のDJIデータを取得します(出典:
Finance.yahoo.com )。
ダウ・ジョーンズ工業平均(DJI)指数値
式X [t] / X [t-1]-1に従って計算された一連の引用率の増分
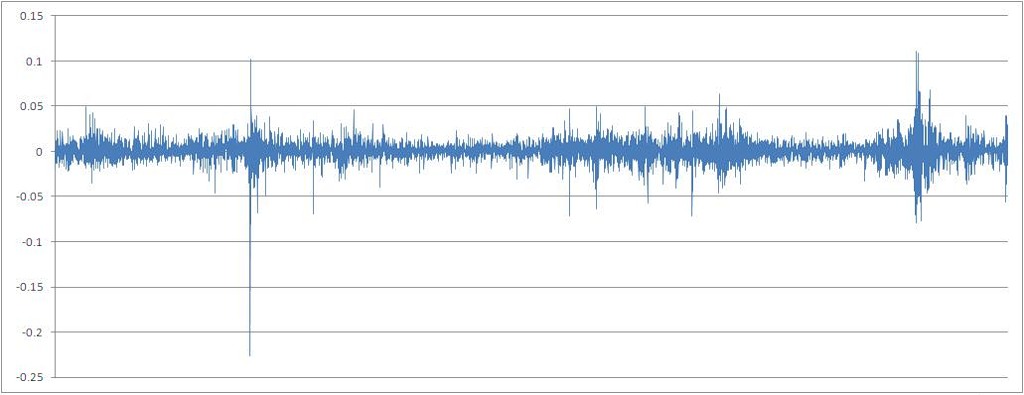
調査した連続的な、本質的に変数を離散型にするために、0.01(1%)に丸められた一連のパーセンテージ増分に渡します。 連続変数の相互情報の計算は、技術的には可能ですが、nの値が非常に大きいため、情報変数ではありません。これは、ランダム変数が受け入れる属性値の有限セットです。

記事で使用されている情報理論的アイデアの基本概念
(すべての式と理論は、
en.wikipedia.orgとキーワードで検索できる多数のモノグラフから借用されています。)
情報理論はコミュニケーション理論と密接に発展しており、私はこの伝統から離れません。
情報とは何ですか?
データの特定の送信機と受信機があると想像してください。 送信機は、離散変数Xを送信します。これは、限られた数のxの値を取ります(これはアルファベットとも呼ばれます)。 特定の各値の実現確率はゼロとは異なります。それ以外の場合、そのような値は分析から単に除外されます。 変数がとる値の空間での確率密度関数の形式は任意です。 各可能な値のすべての確率の合計は1です(合計が0の場合、思考のさらなる列は意味がありません)。
受信者は、Xの送信された値を認識します。または、値を受信した時点でイベントが発生したと言うことができます-変数Xは値xを取ります。 そして、私たち、つまりオブザーバーは、どんな種類のイベントが起こるか(言い換えれば、レシーバーがどのような値を取るか)を知るほど、このシステムのエントロピーは大きくなり、このイベントの実装がもたらす情報は多くなります。
これは、情報エントロピー(理論物理学のエントロピーから借用された概念)が、イベントの可能性とその即時の実現から成る抽象的なシステムの不確実性の定量的尺度であることを意味します。 うーん、それは本当に抽象的に聞こえます。 しかし、これがこの理論の強みです。これは、最も広いクラスの現象に適用できます。
しかし、情報とは何ですか? また、特定のイベントの実装においてシステムに残されたエントロピーまたは不確実性の量を特徴付ける定量的尺度でもあります。 したがって、情報は定量的にエントロピーに等しくなります。
システムに実装されている値の範囲全体について話している場合、平均情報または情報エントロピーについて話している。 この値は式によって計算されます:

ランダム変数の単一の実装の情報について話している場合、独自の情報について話している:

たとえば、公正なコインを繰り返しフリッピングする実験は、1ビットに等しい平均情報を持つシステムです(式に2を底とする対数を代入する場合)。 さらに、各投げの前に、尾またはワシが等しい確率で落ちることを期待し(これらのイベント!互いに独立しています!)、不確実性は常に1です。そして、コインの落下側の不平等な確率でこのシステムの情報エントロピーはどうなりますか? たとえば、ワシは0.6の確率で落ち、尾は-0.4の確率で落ちます。 カウントして取得:0.971ビット。 実験の不確実性はすでに小さくなっているため、システムのエントロピーは減少しています。尾よりもワシの方が多いと予想されます。
送信機と受信機の例に戻ると、それらの間の通信が完全に良好な場合、(広義の)情報は常に100%正しく送信されます。 言い換えると、送信機と受信機の間の相互情報は、受信機自体の平均情報に等しくなり(イベントの実装を象徴する)、送信機からのデータが受信機によって受信されたデータとまったく接続されていない場合、それらの間の相互情報は0になります。送信機送信機は、受信機が受信しているものについては何も言いません。 情報の損失がある場合、相互情報は0から受信者の平均情報になります。
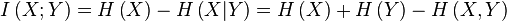
この記事で書いた問題のコンテキストでは、相互情報は、レシーバー(従属変数)とトランスミッター(独立変数)の間の任意のタイプの依存関係を見つけるためのツールとして機能します。 一対の変数間の相互情報の最大化は、過去の実装に関してランダムな値の実装に何らかの決定性が存在することを示しています。 もちろん、朝の鳴き鳥の構成から、株式取引に関するオンライン出版物の特定の単語の頻度まで、任意のものを独立変数として取ることができます。 「真実は近くのどこかにあります。」
それでは、データソース(http://ru.wikipedia.org/)のエントロピーを計算しましょう。

このデータソースの平均情報(または単にエントロピー)(2を底とする対数で計算)は2.098ビットです。
ランダム変数間の相互情報は、情報エントロピーの概念(http://ru.wikipedia.org/)を通じて計算されます。
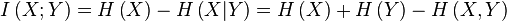
従属変数間の相互情報の値のヒストグラム-終値によって計算されたインデックスの割合の増分-と1から250ステップ前にシフトした値。
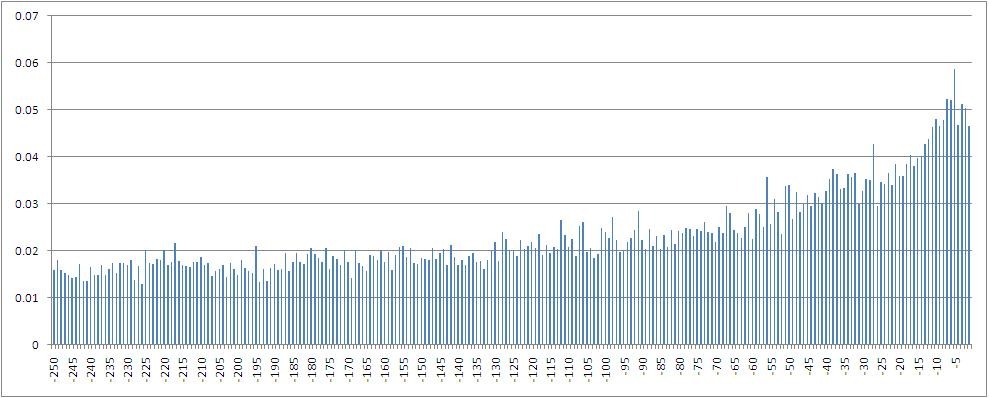
特に、ラグ5の変数、つまり1週間前に取引が行われた値では、最大の相互情報が考慮されることがわかります。 また、ラグ空間に浸されると相互情報量が減少することは明らかです。
取得した相互情報量の値セットの確率密度分布関数の形式:

参考のために、人工的な時系列を生成します。 ソース
www.random.orgは、属性の値のシーケンスを指定する一連の整数のソースとして選択されました。 サイトの情報によると、それらは真の乱数を提供します(PRNGとは異なり、擬似乱数ジェネレーター)。
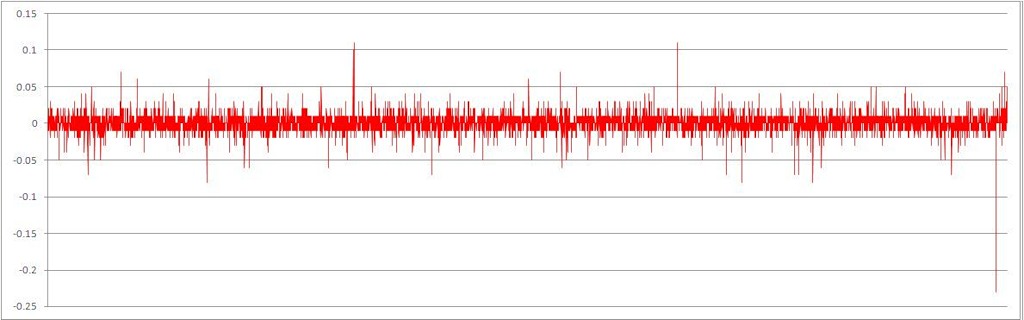
ランダムに混合された時系列順の結果の一連の増分

目で見ると、データがどれだけ静止しているかがわかります。
丸められた値を持つ同じシリーズ
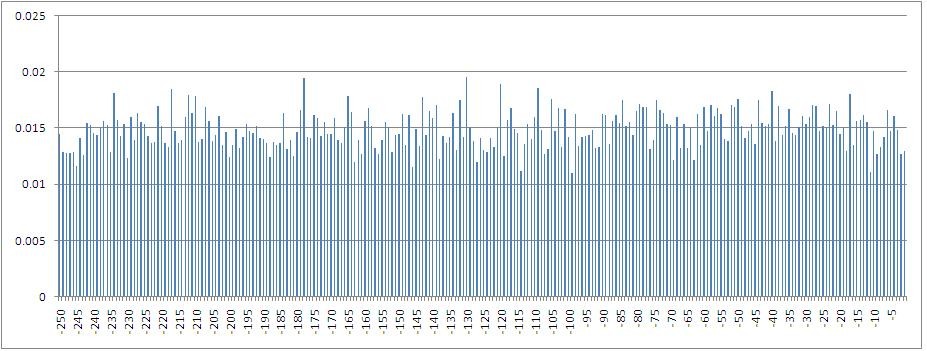
従属変数とその値の間の相互情報の値のヒストグラムで、人工の時系列の増分に沿って1から250ステップの時間でシフトします(属性の値の空間で同じ形式の確率密度関数を維持します)
特定のサンプルの確率密度分布関数のタイプ:

相互情報の計算で考慮される2つのケースの比較

相互情報量の値の取得サンプルがどれだけ異なるかを目で見ることができます。
相互情報の計算値の2つのサンプルの差(確率密度関数の形式の差)の重要性の仮説を検証します-初期時系列と人工時系列について。 ノンパラメトリック検定を使用して、コルモゴロフ-スミルノフ法により統計を計算します(コルモゴロフ-スミルノフ検定を使用して、2つの独立した値のサンプルを比較し、サンプル値間の差の統計的有意性を判断します。この目的のために、マンおよびホイットニーU検定を使用します)。
結果:受け入れられたしきい値有意水準0.05でp = 0.00。
Mann and Whitneyの方法によるU検定の結果:p = 0.00。
どちらの場合も、属性値のサンプル間の差の仮説が受け入れられることがわかります(pが0.05未満)。
自然な財務データ(少なくともDJIインデックス)では、増分引用符の間に任意のタイプの統計的に有意な依存関係があると結論付けることができます。 つまり、このような一連のデータをランダムと見なすことはできません。 理論的には、たとえばニューラルネットワークを使用して、そのようなシリーズの将来の値を予測する可能性のスペースがあります。
PS:コメント、批判にうれしいです。