こんにちは、ハブラ。
今日は
、F。ハイダーの認知バランスの理論についてお話したいと思います。
理論自体は
、認知的対応の
理論のクラスに属します。 このクラスの理論を使用して、ソーシャルネットワークを含むソーシャルインタラクションを数学的に記述しようとすることができます。
認知バランスの理論は、彼の周りの世界に関係する人は常にバランスの状態にあるか、あらゆる可能な方法でそれのために努力していると言います。
はじめに
元のモデルはPOXモデルの名前を指定し、次のコンポーネントで構成されていました。
- Pは特定の人格です。
- O-特定のオブジェクト(人格を含む)、この人格に関連してP-好きな/嫌いの形式で何らかの関係を経験する;
- Xは、Pが何らかの関係を経験し、それ自体がオブジェクトOに関して何らかの関係を経験する特定の他の人格であり、Pはそれについて知っています。
この理論によれば、比率POは、次のように関係PXとOXによっても決定されます。
- 私の友人の友人は私の友人です。
- 私の敵の友人は私の敵です。
- 友達の敵は私の敵です。
- 私の敵の敵は私の友人です。

たとえば、PがOを愛する場合(Wikipediaから)。 PはXが好きではありません。 PはXがOを作成したことを知っています。 この理論に従って、Pを次の可能な結論に導くことができます。
- Xはそれほど悪くない
- O-あまり良くない
- XはOの著者ではありません。
このモデルに基づいて、独自の何かを構築し、結果を徐々に複雑にすることができます。
だから、それを仮定します:
- A、B、Cの3つの特定の主題があります。
- すべてのサブジェクトは相互に関係があり、これらの関係は相互に関係があります(これにより、 有向グラフから単なるグラフに切り替えて、初期モデルを簡素化できます)。
グラフの頂点を介して主題を示し、アークを介して主題間の関係を示す場合、次の形式のトライアドを考慮することができます。

ここで、関係は正(+)と負(-)にしかできないと仮定します。
次に、モデルの8つの可能な状態を指定できます。
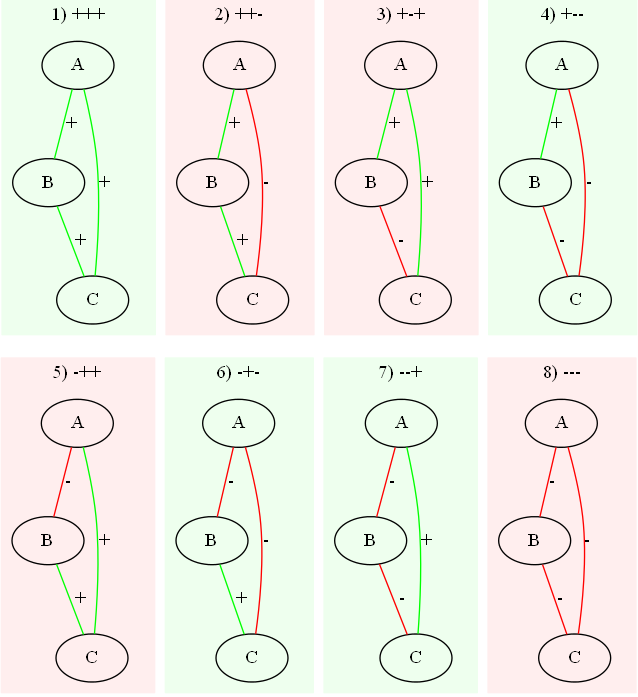
接続の兆候の積が正の数である場合、トライアドは調和または安定しているという主張があります。 つまり、3つの正の接続、または2つの負の接続と1つの正の接続がある場合に可能です。 つまり、ケース1、4、6、7は調和的で安定しており、ケース2、3、5、8は不安定です。
テーブルの形式では、次のようになります。

不均衡なトライアドは、バランスが取れるようになります。 それぞれに3つの可能なシナリオがあります。 いわゆる移行キューブを取得します。
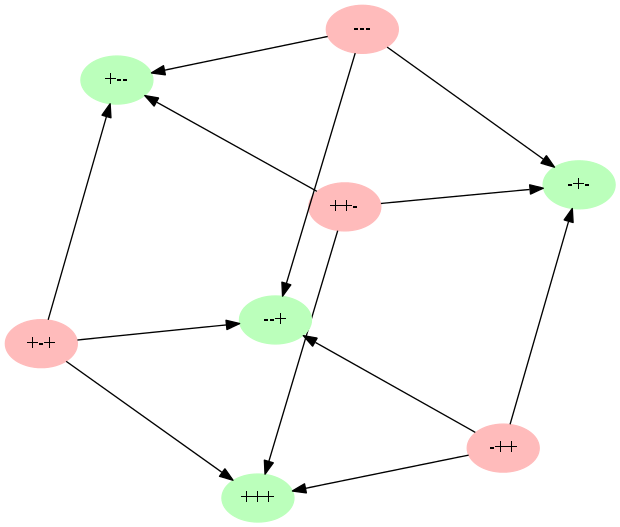
さらに、トライアドの開発のオプションも同様に可能性があります。
中性結合がトライアド内に追加されると、可能な状態の数は27に増加します。さらに、すべての関係が確立されていない場合、それらのうちの19が縮退したケースになります。 この場合、欠落している接続はまったく関与しないか、上記のバランスの取れた接続を目指します。 この情報に基づいて、移行キューブは次のようになります。

つまり、最初の場合と同様に、トライアドとそれらの間の遷移のバイナリツリーを取得します。
関係の重みが互いに等しくない場合、ある状態から別の状態への遷移の確率が異なり、トライアド内の関係がどのように変化するかを予測できます。
しかし、真空中の球形の馬のような孤立したトライアドは、紙の上にしかできません。 現実の世界には、多かれ少なかれ大きな集団があり、その中で相互作用は内部のトライアドと同じ原理に基づいて構築されています。 この場合、グループのバランスは、すべてのトライアドのバランスによって決まります。
グループの2つの状態のうち、よりバランスの取れた状態であり、よりバランスの取れたトライアドがあります。
いくつかの式
グループのバランスを評価するために、特別なインデックスを入力できます。
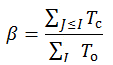
Tcはバランスの取れたトライアドの数で、Toはトライアドの総数です。
グループ内のバランスの指標が高い大規模な接続サブグループは、他のすべてのサブジェクトと関係がある別の拡大サブジェクトとして表すことができます。
大規模なグラフ(人、オブジェクト、それらの間の関係)は、大規模なグループが2つの小さなサブグループに分割されている場合にのみ、バランスの取れた状態にあるという構造定理があります。
確かに、1つのサブグループが大きな正のインデックスを持つ2つの連結されたサブグループに精神的に分割され、2番目のサブグループがそのままの場合、1つのプラスと2つのマイナスを持つ古典的なバランスのとれたトライアドを取得します。 すべての被験者が互いに肯定的な関係を持つことができるというトピックについて推測することができますが、そのような結果の確率は、2つの競合するサブグループ(それぞれトライアドNo.1とトライアドNo.4、6、7)に分割された場合よりも3倍低くなります。
グループにN人がいると仮定すると、それらの間の可能な関係の数は
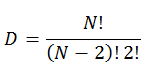
関係が正(+)、負(-)、中立(0)の場合、可能なすべての状態の数は
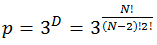
トライアドの総数は

また、自発的な移行であるceteris paribusは、次の規則に従うことに留意する必要があります。
- 関係(0)→(+)と(0)→(-)の自発的な遷移の確率は、1に近いです。
- 関係の自発的な遷移の確率(+)→(0)、(-)→(0)、(+)→(-)、(-)→(+)はゼロに近いです。
最初の理由は、人々のグループでは、通常誰もがお互いを知り合い、1つまたは別の関係が確立されるという事実によるものです。 2つ目は、常にコミュニケーションをとっている相手を忘れたり、彼に対する態度を正反対に変えたりすることはかなり難しいという事実によって説明されます。
これらの条件を考えると、次の遷移キューブはトライアドに対して機能します。
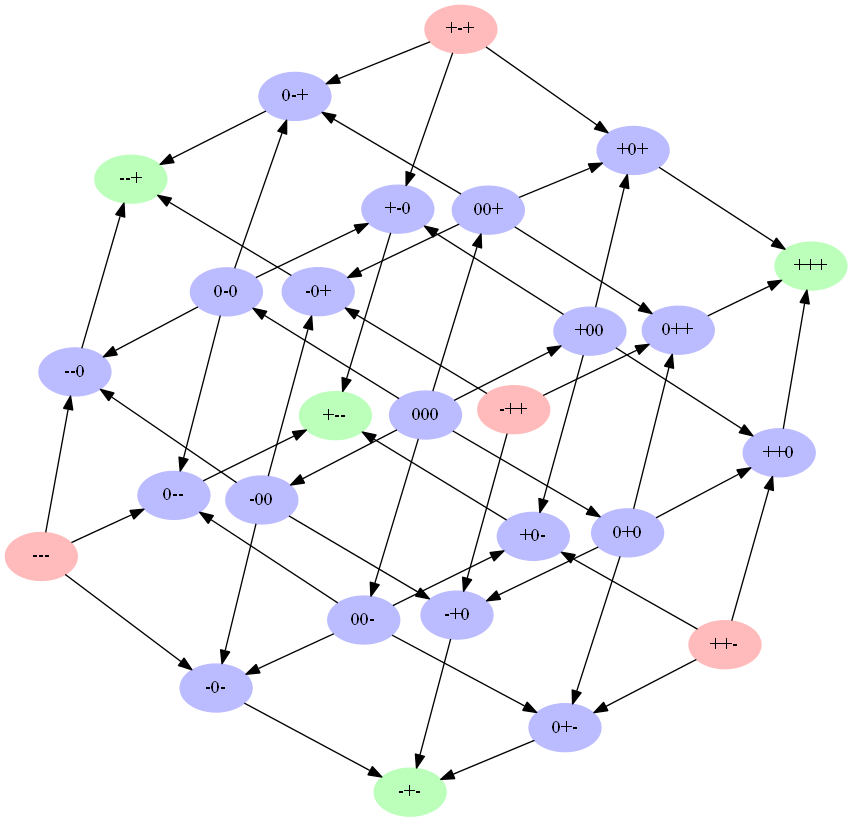
人が参加するバランスのとれたトライアドの数も、自発的な移行に影響します。 彼はバランスのとれたトライアドの数が増加する状態になろうとしています。 この場合、このような遷移の可能性を判断するために、ローカルリンクバランスインデックスが使用されます。 明らかに、1つの関係がグループのすべての可能なトライアドに参加することはできません。 したがって、評価には、この接続が関与するトライアドのみが使用されます。
それから

ここで、T-特定の接続の平衡トライアド、Tlock-特定の接続のトライアドの総数。 評価の原則は、グループ全体と同じです。
絵を完成させるために、関係により滑らかな変化を加えることができます-正、負、またはゼロだけでなく、特定の間隔で囲まれた重みrもあります。 たとえば、-RからRまでの範囲で、R = 0.5; 1; 5; 10 ...この場合、これらの関係が変化する法則を指定する必要があります。 多くの作業で、ヒステリシスはこれらの目的に使用されます。 他の作品は社会的距離の概念を考慮に入れています。
この場合、時間の経過とともに関係が変化する法律を作成できます。

ここで、G(r、R)=(1-(r / R))^ 2、r(i、j)はi番目とj番目の被験者の比率です。
例
ボーナスとして、いくつかのアニメーションgif。
各画像の下部に、一般的なバランスインデックスが表示されます。
シンプルなトライアド用。
最初の小さな矛盾にもかかわらず、3つとも友好的です。

2つは3つ目の友人です。

4人用。
誰もがみんなと友達です。

対立は2対2です。
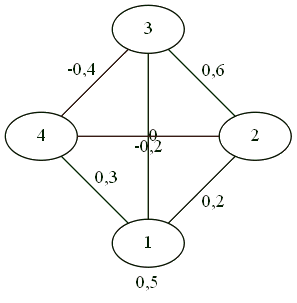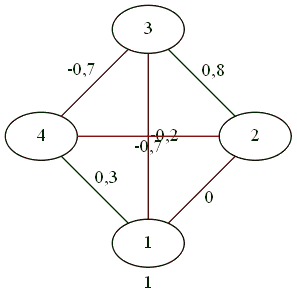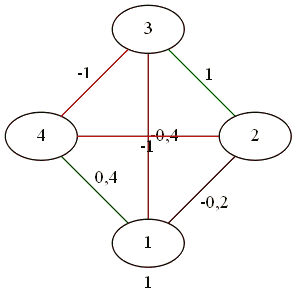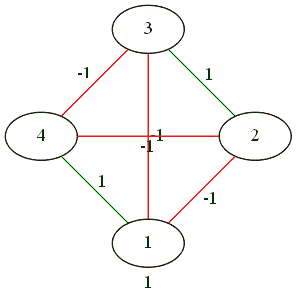
複雑なジェスチャーの結果、3対1。
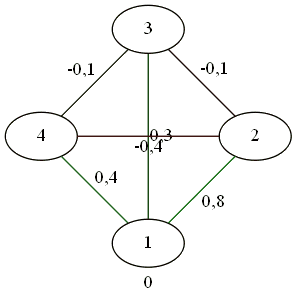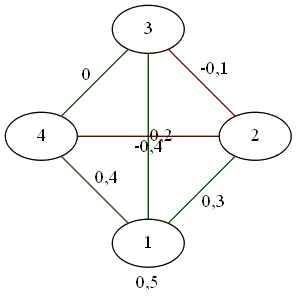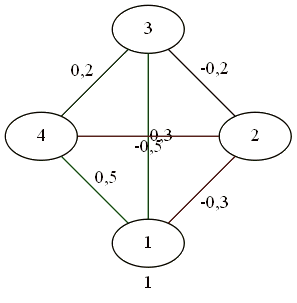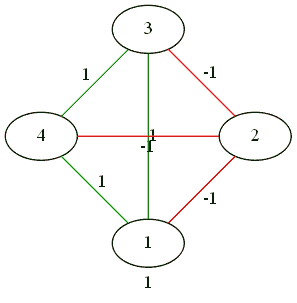
記事を散らかさないために、残りの例は私の
アルバムで見ることができます(5、6、10、および25)。
私は、多くの人々にとって、10 MB未満の重いgifを受け取ったことを警告したいと思います。
そしてもう一つの発言。 プロトタイププログラムはC#で記述され、
Graphvizは視覚化
に使用されました。
また、トライアドを計算するとき、2次、3次、およびそれ以上の次数の近隣の状態を考慮することができます。 クラスターに分割し、クラスターを1つの大きな人物に結合します。 これらまたはそれらの主題の間の関係に関するすべての情報を常に知っているわけではないという事実を考慮に入れることができます。 または、それらまたは他のサブジェクト自体が情報の完全性を持っていません。 また、何らかの外部の影響を使用することも、アークの重みが異なる場合や、ある人が他の人と安定した良好な関係を維持するためのリソースを持っている場合もあります。 または彼らの不在。 最初にバランスのとれたグループからの生存の例を考えることができます。
最終的に、元のモデルに戻って有向グラフを使用できます。つまり、被験者間の関係が非対称になります。 この場合、アークの数は2倍になりますが、計算の原則は変わりません。
ただし、これはすべて、はるかに深刻な研究の対象となっています。
誰かがこのトピックを読むことに興味があるなら、ここに作品へのリンクのセットがあり、そこから始めて、私はこの記事を作りました。
それだけです。 ご清聴ありがとうございました。
リンク1リンク2リンク3リンク4リンク5