実験の数学設計を使用したソフトウェアパフォーマンス分析

「早すぎる最適化はすべての悪の根源です」
アンソニー・ホア

Habrのすべてのユーザーを歓迎します！
この記事は、私の科学研究の有用な副産物として浮上しました。 以下に示すアイデアがあなたにとって興味深く有用であると思われたらうれしく思います。また、実際のプロジェクトでの応用とさらなる開発が得られればさらに嬉しいです。

ソフトウェアパフォーマンス（ソフトウェア）は、ソフトウェア製品の開発における重要な側面です。 この問題の関連性は、ソフトウェアの複雑性と重要性がますます高まっているためです。 パフォーマンスには特に注意が払われます。

• エンジニアリングおよび科学の開発では、複雑で長い計算が頻繁に実行され、クラスターシステムのプロセッサー時間は高価で制限されています。
• ページ生成時間がユーザーにとって重要であり、サーバーの容量に直接依存するWebアプリケーションでは、
• 組み込みソフトウェア製品など

ソフトウェア製品のパフォーマンスを徹底的に分析することで、機器自体のコストとパフォーマンスを維持するコストを大幅に削減し、ソフトウェアユーザーのロイヤリティを高めることができます。
ソフトウェアに関するパフォーマンスの概念は、 生産性または反応性のいずれかを意味します。

• 生産性-単位時間あたりにシステムによって処理される情報の量。
• 反応性-システムへの入力データの表示と、対応する出力情報の表示との間の時間。

このホワイトペーパーでは、ソフトウェアのパフォーマンスの尺度として反応性を考慮します。 このような選択は基本的なものではなく、可能なだけでなく、実験での測定を簡単にするためにのみ行われています。 処理された情報の量を常に測定できるとは限らないため、生産性を考慮するには、テストを実施する手順を複雑にする必要があります。 システムによるデータ処理時間の見積もりは、以下を含む実装がはるかに簡単です。 テストプロセスの自動化。
ソフトウェアを分析するとき、研究者が直面する最も明白で論理的なタスクは生産性を高めることです。 正式には、最適化の問題があり、この調査のコンテキストでは、ソフトウェアシステムによる着信情報の処理時間を最小化するタスクがあります。 したがって、最適化基準は何らかの関数です

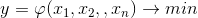
ここで（1）

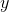• -情報処理時間;
• -システムパフォーマンスに直接または間接的に影響を与える可能性のあるすべてのパラメーター（要因または影響要因）。
• i番目の要因の決定の領域であり、これは問題の制限です。

プログラムのパフォーマンスに影響する要因の全体を選択することは、些細な問題ではありません。 原則として、最新のソフトウェアは非常に複雑なシステムであり、膨大な数の接続と依存関係があります。 そして、それはソフトウェア製品自体の複雑さだけではありません。 すべてのプログラムには、ランタイムランタイムがあり、オペレーティングシステムで動作し、他のサービスやソフトウェアとやり取りします。これらの要素はすべて、内部接続と依存関係の数が少ない個別の複雑なシステムを表します。 因子の相互依存関係（ペアおよび/または線形だけでなく）も追加すると、因子の考えられるすべての組み合わせの信じられないほどの数が得られます。
たとえば、データベース（DB）で動作し、そこに格納されている情報の統計処理を実行するプログラムを考えてみましょう。 生産性に影響する要因の例は次のとおりです。

• コンピューターのRAMの量。
• ハードディスクのアクセス速度。
• 最大周波数と平均プロセッサ負荷。
• DBMS設定など

これらの要因間の依存関係の可能性は明らかです。 たとえば、RAMの量を増やすと、ハードドライブへの頻繁なアクセスの必要性を減らし、その結果、対応する要因の影響を減らすことができます。

影響因子の最適値を検索するには、つまり 最適化の問題（1）を解決するには、次のオプションを提案できます。

• 影響因子の値のすべての可能な組み合わせの完全な列挙;
• 多数の組み合わせのランダムな選択と、その後の最適なオプションの選択。
• システムの分析的研究;
• 特殊なソフトウェアの使用。
• 数学モデルの使用。

これらのオプションにはすべて長所と短所があります。 徹底的な検索を使用すると、目的のパラメーターが見つかると考えることができますが、多くの要因とその値のオプションがあるため、可能なすべての組み合わせの数が多すぎて、実験に時間がかかりすぎます。 Nの可能なすべての組み合わせの数は、組み合わせ規則によって見つけることができます。

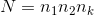
ここで（2）

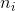• -i番目の係数の値のオプションの数。

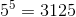
次に、5つの因子と各因子の5つの可能な値を使用して、 組み合わせ。
最適な組み合わせをランダムに選択すると、結果のソリューションはグローバル最適化から非常に遠くなる可能性があります。
システムの分析的研究は、ソースコードなしで既存の製品を分析する場合、しばしば困難または不可能です。 さらに、そのようなアプローチでは、ソフトウェアで使用されるすべてのアルゴリズム、コンポーネントの関係および依存関係を研究者が完全に理解する必要があります。
プロファイラ[5]などの特別なソフトウェアツールを使用すると、プログラムコードの実行に関する統計情報（メソッド呼び出しの回数、メソッドの平均実行時間など）のみを取得できます。 この場合の最適化は、いわゆる 使用されるアルゴリズムのボトルネックと最適化。 このようなアプローチは非常に人気がありますが、問題に対する望ましい解決策を得ることができません（1） 。
ソフトウェアパフォーマンス分析の数学モデルは、国内外の著者によって繰り返し検討されてきました。 [1] 、 [2 ]では、ソフトウェア開発のさまざまな段階でこの問題を解決する独自のアプローチが提案されました。
要約すると、提案された解決方法の主な欠点は次のとおりです。

• 測定時間が長すぎる。
• プログラム分析に基づいて結論を引き出す研究者の能力に依存。
• アプリケーションと使用の複雑さ。

上記の困難を克服し、問題を解決するために、実験の数学的計画（MPE）の理論で開発された装置を使用することが提案されています。
ソフトウェアパフォーマンスの分析へのMPEの適用性について詳しく説明します。 実験計画の基本的な考え方の1つは、研究対象のサイバネティックス抽象化オブジェクトにブラックボックスを使用することです[3] （ 図1を参照）。


図 1.ブラックボックスの抽象化。

このような抽象化は、非常に複雑なため、調査対象の現象またはオブジェクトの内部メカニズムを考慮することを拒否することを意味します。 現象の分析は、オブジェクト（要因）および出力特性（応答）に影響する入力パラメーターの分析に限定されます[3] 。
MPEを適用するには、いくつかの条件が必要です[3]。

• 実験の再現性;
• 要因の制御可能性;
• 出力特性の測定可能性と、1つの数値で表現する能力。
• 要因の一意性と互換性など

類推を分析した後、ソフトウェアシステムをブラックボックスと見なすことが可能であると結論付けることができます。 次に、上記の要件が満たされている場合、既存のMPE装置全体を使用してパフォーマンスを調査できます。
例として、MPEを使用してソフトウェアシステムのパフォーマンスを分析する方法論を開発するために、Professional Clubsプロジェクトの一部であるWebアプリケーションを検討します[4] 。

ステージ1.事前情報の分析。

ソフトウェア製品に関するアプリオリ情報を分析すると、次のことが判明しました。

• ソフトウェアは、PHPプログラミング言語で書かれたWebアプリケーションです。
• ソフトウェアはApache Webサーバーで実行され、PHPインタープリターはモジュールとして接続されます。
• ソフトウェアはMySQL DBMSを使用してデータを保存します。
• アプリケーション自体を使用してデータキャッシュを有効にすることができます。

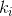
実験の数学モデル[3]として、最も単純なもの-因子間の依存関係のない線形モデルを使用します。 ほとんどの場合、このような仮定と要因の組み合わせは実際の状況に対応していませんが、メソッド自体のテストに使用される可能性があります。 次に、この問題は、係数の値を見つけることに限定されます 回帰方程式

。 （3）

最も高い値を持つ要因は、出力応答に最大の影響を与えます。

ステージ2。影響因子の選択。

表1は、ソフトウェアに関するアプリオリ情報の分析の結果として選択された一連の影響因子を示しています。

表1

ファクター	説明
	MySQL key_buffer_size インデックスを保存するために割り当てられるメモリ量を決定するDBMSチューニングパラメータ[6] 。
	MySQL table_cache 常時開いているデータベーステーブルの数を決定するDBMSチューニングパラメータ[6] 。
	MySQL query_cache_limit クエリ結果をキャッシュするための最大メモリ量を定義するDBMSチューニングパラメータ[6] 。
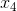	アプリケーションごとのデータのキャッシュ。 オンまたはオフのいずれかです。
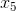	WebサーバーとPHPインタープリターの起動方法。 調査中のアプリケーションは、次の2つの方法で起動できます。 Apache Webサーバー+ PHPモジュール。 Nginx Webサーバー+ php-fpm。

ステージ3.因子の上位レベルと下位レベルの選択。

次に、各因子の上位レベルと下位レベルを選択する必要があります[3] 。 以下、MPEで採用されている表記法を使用します。

• +1は、因子の上位レベルに対応します。
• -1は、因子の下位レベルに対応します。

表2。

ファクター	上位レベル（+1）	下位レベル（-1）
	265 Mb。	16 Mb。
	300	64
	64 Mb。	1 Mb。
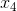	キャッシュはオンです。	キャッシュはオフです。
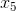	Nginx + php-fpm。	Apache + mod_php。

ステージ4.計画マトリックスを作成し、実験を実施します。

表3は、一連の実験の結果を示しています。

表3

いや						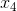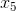y	いや						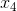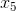y
1	-1	-1	-1	-1	-1	6,909456902	17	+1	-1	-1	-1	-1	6.956250343
2	-1	-1	-1	-1	+1	6,265920885	18	+1	-1	-1	-1	+1	6.27117213
3	-1	-1	-1	+1	-1	1,046864681	19	+1	-1	-1	+1	-1	1,049605346
4	-1	-1	-1	+1	+1	0.959287777	20	+1	-1	-1	+1	+1	0.960128005
5	-1	-1	+1	-1	-1	6.922491238	21	+1	-1	+1	-1	-1	6.94905457
6	-1	-1	+1	-1	+1	6,292138541	22	+1	-1	+1	-1	+1	6,288483698
7	-1	-1	+1	+1	-1	1,047327693	23	+1	-1	+1	+1	-1	1,048429732
8	-1	-1	+1	+1	+1	0.959178464	24	+1	-1	+1	+1	+1	0.959984639
9	-1	+1	-1	-1	-1	6,947828159	25	+1	+1	-1	-1	-1	6.944574752
10	-1	+1	-1	-1	+1	6.269961421	26	+1	+1	-1	-1	+1	6.281574535
11	-1	+1	-1	+1	-1	1,047032595	27	+1	+1	-1	+1	-1	1,047937875
12	-1	+1	-1	+1	+1	0.960076244	28	+1	+1	-1	+1	+1	0.960813348
13	-1	+1	+1	-1	-1	6.954160943	29日	+1	+1	+1	-1	-1	6,952602925
14	-1	+1	+1	-1	+1	6,278223336	30	+1	+1	+1	-1	+1	6.284795263
15	-1	+1	+1	+1	-1	1,048019483	31	+1	+1	+1	+1	-1	1,047952991
16	-1	+1	+1	+1	+1	0.960559206	32	+1	+1	+1	+1	+1	0.960591927

ステージ5.結果の分析。

回帰式（3）の係数は、


。 （4）

結果を表4および図 5に示します 。 2 。

表4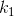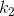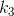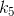

3.97361211	0.0519711	0,0245041	0,0034686	-2.9182692	-0.2483070

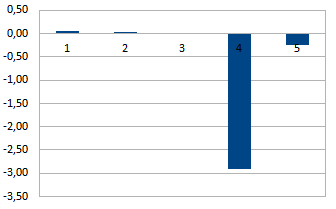
図 2.回帰式の係数。

ステージ6.結論。

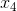
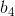
図から 図2は、Webページの生成への主な貢献が要因によって行われることを示しています 、アプリケーション内のデータのキャッシュを特徴付ける。 負の回帰係数 このオプションは、ブラックボックス応答関数を減らすことを意味します。 この例では、これはページ生成時間の短縮を意味します。
厳密に言えば、このような結果は明らかです。アプリケーションによるデータキャッシングを含めるには、DBMSへのクエリの最小数が必要になるからです。 したがって、DBMS設定の影響はわずかになります。 得られた結果は、ソフトウェアパフォーマンスの分析に適用されるMPEの使用の可能性を確認します。

この記事では、ソフトウェアのパフォーマンスの分析に関連して、長い間存在してきた実験の数学的計画法を使用する可能性を検討しようとしました。 このアプローチにより、ソフトウェアシステムの分析で生じる多くの困難を克服し、分析された特性に最も強く影響する要因を特定し、要因間の関係を特定することができます。
もちろん、提示された方法論は、プロファイリングなどのパフォーマンス分析の既存の方法を置き換えるふりをするものではありません。 ただし、このような手法を使用すると、研究者のタスクを大幅に促進できるタスクがいくつかあります。

ご清聴ありがとうございました！

参照資料

1. Dubakov S.A. ソフトウェア開発プロセスにおける情報技術のパフォーマンス分析：dis。 キャンディ。 tech。 科学/ Dubakov S.A. -トムスク、2005年-135秒
2. モイセイチュクL.D. 厳密に階層的な確率ペトリネットに基づいてソフトウェアのパフォーマンスを分析するためのモデルと方法の開発：dis。 キャンディ。 tech。 科学/ Moiseychuk L.D. -サンクトペテルブルク、2002年-152ページ
3. Adler Yu.P.、Markova E.V.、Granovsky Yu.V. 最適条件の検索で実験を計画します。 -M。：Nauka、1976 .-- 279 p。
4. LLCプロフェッショナルクラブ。 -URL ： http : //prof-club.ru/ 控訴日：2011年9月25日。
5. Kaspersky K.プログラム最適化の手法。 メモリの効率的な使用。 -SPb。：BHV-Petersburg、2003。-464 p。
6. MySQLサーバーのシステム変数。 -URL： http : //dev.mysql.com/doc/refman/5.0/en/server-system-variables.html 控訴日：2011年9月25日。