クリッピングアルゴリズム

コンピュータの処理能力の向上に伴い、ますます多くの人々がグラフィックを使用しようとしています。 一見、多くのアルゴリズムは直観的に見えますが、アプリケーションを許容可能な速度で動作させるには、古典的なアルゴリズムを勉強する必要があります。

この投稿は、同じタスク、つまりセグメントを切り離すタスクを目的としたいくつかのアルゴリズムの分析に当てられています。 画像を生成するときに、任意の形状とサイズの形状を取得できます。 多くの場合、モニターは生成された画像全体を表示できません。 また、画面上の画像の領域を設定し、この領域内にのみ画像を表示する必要がある場合もあります。 これらの問題を解決するために、クリッピングアルゴリズムが考案されました。

セグメントの切断

最も単純なクリッピングタスクは、セグメントを切り取ることです。 具体例で定式化します。 出力領域は長方形ABCDによって定義されると仮定します。 例を考えて、三角形PRQをカットオフ図として取ります。



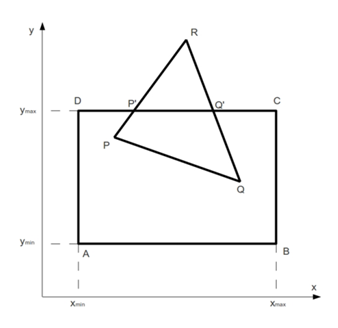
クリッピング処理は完全に自動化される必要があります。 つまり PRQの三角形を描画するには、PQ; PP '; Q' Qの線描画コマンドのみを実行する必要があります。また、点P '; Q'の座標は事前にわかりません。
実際には、セグメントのポイントと出力領域の多数の相対位置が可能です。 この多様性により、アルゴリズムの観点からクリッピング操作が非常に重要になります。 これらの問題を解決するために、クリッピングアルゴリズムが作成されました。

Sutherland-Cohenアルゴリズム

SutherlandとCohenが提案したクリッピングアルゴリズムは非常に興味深いものです。 アルゴリズムの本質は、4ビットコードがセグメントの両端に割り当てられることです：b ₀ 、b ₁ 、b ₂ 、b ₃ 。 この4ビットコードには、出力領域に相対的なポイントの位置に関する情報が含まれています。 実際には、9つの組み合わせが可能です。

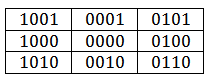
これらのコードを説明してください：
これらのコードを説明してください：

• x≥xminの場合、b ₀ = 0。
• x <x _minの場合、b ₀ = 1。
• x≤xmaxの場合、b ₁ = 0。
• x> x _maxの場合、b ₁ = 1。
• y≥yminの場合、b ₂ = 0。
• y <y _minの場合、b ₂ = 1。
• y≤ymaxの場合、b ₃ = 0。
• y> y _maxの場合、b ₃ = 1。

コードを受け取った後、次のオプションが可能です。

1. コードには0のみが含まれます。これは、セグメント全体がウィンドウ内にあり、全体を描画する必要があることを意味します。
2. コードには同じ位置に1ビットが含まれています。つまり、セグメントはウィンドウの外側にあり、描画されません。
3. 他のすべての場合、セグメントの一部のみがウィンドウ内にあり、これはクリッピングが必要であることを意味します。

最初の2つのケースは、ビットごとの論理演算を使用して簡単に検証できます。 3番目のケースは最大の関心事です。 小さな具体的な例で考えてみましょう。



どちらかの端のコードに単一ビットが含まれている場合、P ₁またはP _2のいずれかがウィンドウの外側からその境界の1つ（またはその継続）に移動します。 つまり ポイントP ₁はポイントRに移動し、P ₂はポイントUに移動します。新しいポイントについては、4ビットコードを再度計算します。 私たちの場合、セグメントの両端はまだウィンドウの外側にあります。 もう1つの移動が必要です。ポイントRがポイントSに移動し、ポイントUがポイントTに移動します。クリッピングプロセスは反復的であることがわかります。 各ステップでセグメントの両端間の距離が減少するため、アルゴリズムは収束していると言えます。 その結果、セグメントが取得されます（この例では（S; T）、表示する必要があります）。
別の例を使用して、このアルゴリズムの動作を考えてみましょう。



セグメントの位置（P ₁ ; P ₂ ）は、完全な可視性の条件または完全な不可視性の条件のいずれにも対応しないため、この場合、ポイントの移動操作にも頼ります。

転送の実行後、セグメントの両端のコードは2番目の条件を満たします。 セグメント全体は画面に表示されません。

中間点アルゴリズム

Sutherland-Cohenアルゴリズムでは、線分とウィンドウの境界との交点を見つけるには、いくつかの反復が必要になる場合があります。 これは、バイナリ検索を使用して交差点の検索を実装する場合は回避できます。 このアイデアはSprullとSutherlandによって提案されました。 このアルゴリズムのソフトウェア実装は、Sutherland-Cohenアルゴリズムよりも遅くなりますが、アルゴリズムの基本操作はハードウェアで非常に効率的に実装されるため、ハードウェア実装は高速です。


このメソッドは、上記の4ビットコードも使用します。 これらのコードの助けを借りて、些細な可視性（a）と些細な不可視性（b）のケースが簡単に検出されます。 残りの（重要な）セグメントは2つの等しい部分に分割され、2つの新しく取得されたセグメントに対してチェックが実行されます。 分割とチェックは、ウィンドウの側面との交差が検出されるまで、または線がポイントに縮退するまで実行されます。 セグメントが縮退した後、その可視性を判断し、結果に応じて、現在に描画するかどうかを決定します。
セグメントcについて考えます。 明らかに、このセグメントは完全にウィンドウの外側にありますが、すぐに拒否することはできません。 そのため、半分の除算を実行し、セグメントの一部を除外します。 分割は、セグメントがポイントに変わった瞬間に終了します。 結果のポイントが不可視であることを確認した後、セグメント全体を描画すべきではないと結論付けます。
セグメントdも簡単に定義されていません。 2つの半分に分割すると（ポイント3）、両方の半分で同じ結果になります。 セグメント（3; 2）はポイント4で半分に分割されます。理論的には、セグメント（3; 4）をすでに描画できますが、これはあまり効果的ではありません。 ポイント4をポイント1から最も遠い可視ポイントとして記憶し、ウィンドウの下部境界と交差するまでセグメント（4; 2）を分割し続けることがより正確です。 結果のポイントは、ポイント1から最も遠い可視ポイントと見なされます。 セグメント3; 1も同様に処理され、可視ポイントがポイント2から最も遠い位置に配置されます。次に、これら2つのポイント間で描画が実行されます。
タイプdのセグメントの場合、セグメントの端から最も遠い可視ポイントの2つのバイナリ検索を実行する必要があります。 タイプeのセグメントの場合、バイナリ検索のいずれかは不要になりました。

Kirus-Beckアルゴリズム

Kirus-Beckアルゴリズムの作業では、区間のパラメトリック表現が使用されます：P _s （t）= P ₁ +（P ₂ -P ₁ ）* t;t∈[0; 1]。 このアルゴリズムにより、長方形のウィンドウだけでなく、凸多角形によるクリッピングも可能になります。
切断ポリゴンの別のエッジE _iを考えます。 このエッジの法線を切断ポリゴンの外側に向けます。 また、切断ポリゴンは反時計回りに回避されると想定しています。 次に、エッジがベクトルP _{（E （i 1 ） ）} P _{E i 2の}場合、法線N _{E i}は比例します（y _{E i 2} -y _{E i 1} ; x _{E i 1} -x _{E i 2} ）。
エッジが存在する線をL _iで示します。 次に、直線L _iで切り取られた領域は、ベクトル（PP _{E i} ）とN _{E i}のスカラー積が0より大きい点Pに対応します（P _{E i}はエッジE _i上の任意の点です）。 セグメントが存在する直線とカットオフラインL _iの交点は、方程式（（P _s （t）-P _{E i} 、N _{E i} = 0.この方程式を解くと、tが見つかります。
説明したアルゴリズムでは、P ₁からP _2にセグメントに沿って移動するときにポイントが通過する方向（ウィンドウの内側または外側）が重要です。 これは符号（（P ₂ -P ₁ ）、N _{E i}によって決定されます。次のような交差点を示します。



線L _iとのすべての交点について座標tが計算された後、潜在的に着信する最大座標と潜在的に発信する最小座標を選択する必要があります（t _VxMax ; t _OutMin ）。 セグメントP ₁ P _2が位置するラインがカットオフポリゴンと交差する場合、t _BxMax <t _{OutMinになり}ます。 この場合、交点[t ₁ 、t ₂ ] = [t _BxMax 、t _OutMin ]∩[0,1]が空でない場合、P _s （t ₁ ）P _s （t ₂ ）が望ましいカットオフセグメントになります。この場合、セグメントはカットオフ領域の完全に外側にあります。

もちろん、クリッピングのトピックはこれらのアルゴリズムで終わりではありません。 別の問題は、ポリゴンクリッピングアルゴリズムです。 トピックがhabrasocietyにとって興味深いものである場合、私は間違いなくこのトピックを明らかにします。