この記事には、ステレオビジョンで使用される数学的装置に関する基本情報が含まれています。 それを書くというアイデアは、特にOpenCVで実装されたアルゴリズムを使用して、ステレオビジョンメソッドで作業を始めた後に生まれました。 これらのアルゴリズムは、多くの場合、「基本行列」、「エピポーラ幾何」、「三角測量」などのさまざまな概念を指します。 コンピュータービジョンに関する非常に優れた書籍があります。これには、ステレオビジョンや必要なすべての概念が記載されていますが、多くの場合、初心者には情報が多すぎます。 ここでは、短い形式で、ステレオビジョンがどのように機能するかに関する基本的な情報とそれに関連する基本的な必要な概念を示します。

• 射影幾何と均一座標
• カメラモデル
• エピポーラジオメトリ（エピポラルジオメトリ）、基本および必須マトリックス（基本マトリックス、必須マトリックス）
• ステレオポイントの三角形分割
• 深度マップ、視差マップ、およびその計算の背後にある考え方

この記事のほとんどすべての資料は、R。HartleyおよびA. Zissermanによる「コンピュータービジョンの複数ビュージオメトリ」に基づいており、深度マップの構築に関するセクションは、Gary Bradski、Adrian KaehlerによるLearning OpenCVの資料に基づいて説明されています。

記事の内容を理解するには、分析幾何学と線形代数の一般的な概念を持っているだけで十分です。行列、ベクトル、スカラー、ベクトル積が何であるかを知ることです。

1射影幾何と同次座標

射影幾何学は、立体視幾何学において重要な役割を果たします。 射影幾何学にはいくつかのアプローチがあります：幾何学（ユークリッド幾何学、公理のような幾何学オブジェクトの概念を導入し、これから射影空間のすべてのプロパティを導き出す）、分析的（ユークリッド幾何学への分析的アプローチのように座標ですべてを考慮する）、代数的です。

さらなる議論のために、射影幾何学への分析的アプローチの理解が主に必要であり、以下に提示されるのは彼です。

射影平面のポイント。 2次元の射影空間（射影平面とも呼ばれます）を考えます。 通常のユークリッド平面では、点は射影平面上の座標のペア（ x 、 y ） ^Tで記述されますが、点は3要素ベクトル（ x 、 y 、 w ） ^Tで記述されます^。 さらに、ゼロ以外の数値aの場合、ベクトル（ x 、 y 、 w ） ^Tと（ ax 、 ay 、 aw ） ^Tは同じ点に対応します。 また、ゼロベクトル（0,0,0） ^Tはどの点にも対応せず、考慮の対象外となります。 このような平面点の記述は、同次座標と呼ばれます。

射影平面の点は、通常のユークリッド平面の点に関連付けることができます。 w ≠0の座標ベクトル（ x 、 y 、 w ） ^Tについて、ユークリッド平面の点を座標（ x / w 、 y / w ） ^Tに関連付けます^。 w = 0の場合、つまり 座標ベクトルの形式は（ x 、 y 、0 ^T ）であり、この点は無限大にあると言います。 したがって、射影平面は、無限遠からの点で補われるユークリッド平面と見なすことができます。

座標ベクトルを最後の成分で除算してから（ x 、 y 、 w ） ^T →（ x / w 、 y / w ） ^Tを破棄することにより、同次座標（ x 、 y 、 w ） ^Tから通常のユークリッド座標に移動できます そして、ユークリッド座標（ x 、 y ） ^Tから、座標ベクトルに1を追加することにより、同次座標に進むことができます：（ x 、 y ） ^T →（ x 、 y 、1） ^T

射影平面上の線。 射影平面上の線は、点のように、3要素ベクトルl =（ a 、 b 、 c ） ^Tによって記述されます^。 繰り返しますが、線を記述するベクトルはゼロ以外の係数まで決定されます。 この場合、線の方程式は次の形式になります： l ^T x = 0。

a ² + b ² ≠0の場合、通常の直線ax + by + c = 0のアナログがあります。そして、ベクトル（0,0、 w ）は無限にある直線に対応します。

三次元射影空間。 射影平面との類推により、3次元射影空間の点は、同次座標（ x 、 y 、 z 、 w ） ^Tの4成分ベクトルによって決定されます^。 繰り返しますが、ゼロ以外の数値aの場合、座標ベクトル（ x 、 y 、 z 、 w ） ^Tと（ ax 、 ay 、 az 、 aw ） ^Tは同じ点に対応します。

射影平面の場合と同様に、3次元ユークリッド空間と3次元射影空間の点の間で対応を確立できます。 w ≠0の同次座標（ x 、 y 、 z 、 w ） ^Tのベクトルは、座標（ x / w 、 y / w 、 z / w ） ^Tのユークリッド空間の点に対応します^。 そして、フォーム（ x 、 y 、 z 、0） ^Tの同次座標のベクトルを持つ点について、彼らはそれが無限遠にあると言います。

射影変換。 さらなるプレゼンテーションに必要となるもう1つのことは、射影変換（ホモグラフィ、射影変換-英語文学）です。 幾何学的な観点から見ると、射影変換は、直線を直線に変換する射影平面（または空間）の可逆変換です。 座標では、射影変換は非縮退正方行列Hとして表されますが、座標ベクトルxは次の式に従って座標ベクトルx 'になります： x ' = H x 。

2投影カメラモデル

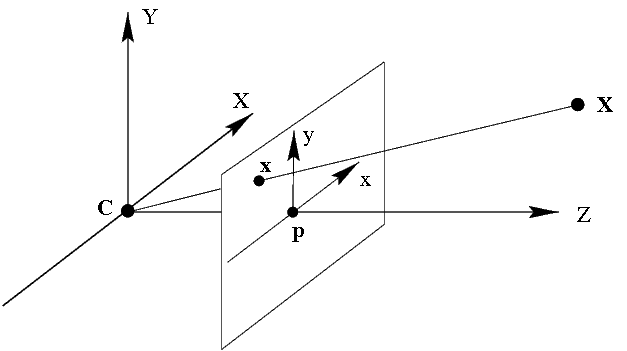
図1： カメラモデル。 Cはカメラの中心、 Cpはカメラの主軸です。 3次元空間の点Xは 、画像平面上の点xに投影されます。

現代のCCDカメラは、投影カメラ、ピンホールカメラと呼ばれる次のモデルを使用してよく説明されています。 射影カメラは、カメラの中心、 主軸 -カメラの中心から開始してカメラが見ている場所に向けられたビーム、画像平面-点が投影される平面、およびこの平面上の座標系によって定義されます。 このようなモデルでは、空間Xの任意の点が、カメラCの中心を開始点Xに接続するセグメントCX上の点xで画像平面に投影されます（図1を参照）。

投影式には、同次座標での簡単な数学表記があります。

x = P X

ここで、 Xは空間内の点の同次座標、 xは平面内の点の同次座標、 Pは3×4カメラ行列です。

行列Pは次のように表されます。P = KR [ I | -c ] = K [ R | t ]、ここでKは3×3カメラの内部パラメーターの上三角行列です（特定のビューを以下に示します）、 Rはグローバル座標系に対するカメラの回転を決定する3×3直交行列、 Iは単一の3×3行列、ベクトルc-カメラの中心の座標、およびt = -R c

カメラ行列は、定数x = P Xを使用して投影点の結果を変更しない一定の非ゼロ係数まで決定されることに注意してください。 ただし、この定数係数は通常、カメラマトリックスが上記の形式になるように選択されます。

最も単純な場合、カメラの中心が原点にあるとき、カメラの主軸はCz軸と一致し、カメラ平面上の座標軸は同じスケール（正方形ピクセルに相当）を持ち、画像の中心はゼロ座標を持ち、カメラ行列はP = K [ 私 | 0 ]、ここで

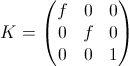
実際のCCDカメラでは、ピクセルは通常正方形のものとわずかに異なり、画像の中心はゼロ以外の座標を持ちます。 この場合、内部パラメーターのマトリックスは次の形式を取ります。

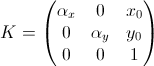
係数f 、αx、αy-は、カメラの焦点距離と呼ばれます（それぞれ、共通およびx軸とy軸に沿って）。

さらに、光学系の不完全な性質により、カメラから取得した画像には歪み歪みが含まれています。 これらの歪みには、非線形の数学的な記録があります。

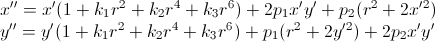
ここで、 k ₁ 、 k ₂ 、 p ₁ 、 p ₂ 、 k ₃は歪み係数であり、光学系のパラメータです。 r ² = x ' ² + y ' ² ; （ x '、 y '）-正方形ピクセルで歪みのない画像の中心に相対的な点の投影の座標; （ x ″、 y ″）-正方形ピクセルの画像の中心に対する点の歪んだ座標。

歪みはオブジェクトまでの距離に依存せず、オブジェクトのピクセルが投影されるポイントの座標のみに依存します。 したがって、歪みを補正するために、カメラから取得した元の画像は通常変換されます。 この変換は、焦点距離が一定（数学的には、内部パラメーターの同じマトリックス）であれば、カメラから受信したすべての画像で同じになります。

カメラの内部パラメーターが既知であり、歪み係数がカメラが較正されていると言う状況で。

3組のカメラ

少なくとも2台のカメラがある場合に、観測ポイントの3次元座標を決定することについて話すことができます。

一対のカメラの行列、キャリブレーション。 ある座標系で行列PとP 'によって定義される2つのカメラがあるとします。 この場合、彼らはキャリブレーションされたカメラのペアがあると言います。 カメラの中心が一致しない場合、このカメラのペアを使用して、観測ポイントの3次元座標を決定できます。

多くの場合、座標系はカメラ行列がP = K [ I | 0]、 P '= K ' [ R '| t ']。 これは、最初のカメラの中心と一致する原点を選択し、 Z軸をその光軸に沿って向けると、いつでも実行できます。

カメラのキャリブレーションは通常実行されます。キャリブレーションテンプレートを複数回撮影するため、空間内での相対的な位置がわかっている画像内のキーポイントを簡単に特定できます。 次に、射影の座標、カメラマトリックス、および空間内のテンプレートのポイントの位置をリンクして、方程式のシステムがコンパイルされ、解決されます（およそ）。

Matlabキャリブレーションツールボックスなど、キャリブレーションアルゴリズムの一般的に利用可能な実装があります。 OpenCVライブラリには、カメラのキャリブレーションと画像内のキャリブレーションテンプレートの検索のためのアルゴリズムも含まれています。

エピポーラジオメトリ。 点の3次元座標を計算する実際の方法の説明に進む前に、両方のカメラからの画像上の3次元空間の点の投影の位置に関連するいくつかの重要な幾何学的特性について説明します。

図2：エピポーラジオメトリ

図2に示すように、2つのカメラがあるとします。Cは最初のカメラの中心、 C 'は2番目のカメラの中心です。 空間点Xは 、左カメラの画像平面のxと、右カメラの画像平面のx 'に投影されます。 左カメラの画像の点xのプロトタイプは、光線xXです。 このビームは、エピポーラ線と呼ばれる直線l 'で第2チャンバの平面に投影されます。 2番目のカメラの画像平面上の点Xの画像は、必然的にエピポーラ線l '上にあります。

したがって、左カメラの画像の各点xは、右カメラの画像のエピポーラ線l 'に対応します。 この場合、右のカメラの画像のxのペアは、対応するエピポーラ線上にのみ存在できます。 同様に、右の画像の各点x 'は、左のエピポーラ線lに対応します。

エピポーラジオメトリは、ステレオペアを検索し、ポイントのペアがステレオペア（つまり、空間内のあるポイントの投影）になり得ることを確認するために使用されます。

エピポーラジオメトリの座標表記は非常に単純です。 キャリブレーションされたカメラのペアがあり、 xを1つのカメラの画像の点の均一座標とし、 x 'を2番目のカメラの画像にします。 次の場合にのみ、ポイントのペアx 、 x 'がステレオペアであるような3×3行列Fが存在します。

x ' T F x = 0

行列Fは基本行列と呼ばれます。 そのランクは2で、ゼロ以外の係数まで決定され、ソースカメラPおよびP 'の行列のみに依存します。

カメラ配列の形式がP = K [ I | 0]の場合、 P '= K ' [ R | t ]基本行列は次の式で計算できます。

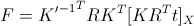
ここで、ベクトルeの表記[ e ] _{Xは次のように}計算されます。

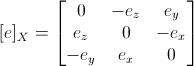
基本行列を使用して、エピポーラ線の方程式が計算されます。 点xの場合、エピポーラ線を定義するベクトルの形式はl '= F xになり、エピポーラ線自体の方程式はl ' ^T x '= 0になります。同様に点x 'の場合、エピポーラ線を定義するベクトルの形式はl = F ^T x '。

基本的なマトリックスに加えて、 E = K ' ^T F Kという必須マトリックスがあります。 内部パラメータの行列が単一である場合、基本行列は基本行列と一致します。 エッセンシャルマトリックスを使用すると、最初のカメラに対する2番目のカメラの位置と回転を復元できるため、カメラの動きを判断する必要があるタスクで使用されます。

ポイントの三角形分割（三角形分割）。 次に、投影の座標からポイントの3次元座標を決定する方法に進みましょう。 このプロセスは、文献では三角測量と呼ばれます。

マトリックスP ₁およびP _2を備えた2つのキャリブレーションされたカメラがあるとします。 x ₁とx ₂は、空間Xの点の同次投影座標です。 その後、次の方程式系を作成できます。

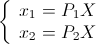
実際には、このシステムを解決するために次のアプローチが適用されます。 最初の方程式にx _1、2番目にx _2をベクトル乗算し、線形従属方程式を取り除き、システムをA X = 0の形式にします。ここで、 Aは4×4のサイズを持ちます。その最後のコンポーネントは1に等しく、3つの未知数を持つ3つの方程式の結果のシステムを解きます。 別の方法は、システムA X = 0のゼロ以外の解を取得することです。たとえば、行列Aの最小の特異数に対応する特異ベクトルとして計算されます。

4深度マップの構築

深度マップは、色ではなくピクセルごとにカメラまでの距離が保存される画像です。 深度マップは、特別な深度カメラを使用して取得できます（たとえば、Kinectセンサーはそのようなカメラの一種です）。また、ステレオ画像ペアを使用して構築することもできます。

ステレオペアを使用して深度マップを作成する背後にある考え方は非常に簡単です。 1つの画像の各ポイントに対して、別の画像のポイントのペアを検索します。 また、対応する点のペアにより、三角測量を実行し、3次元空間での逆像の座標を決定できます。 プロトタイプの3次元座標がわかっている場合、深度はカメラの平面までの距離として計算されます。

対になった点は、エピポーラ線上で探す必要があります。 したがって、検索を簡素化するために、すべてのエピポーラ線が画像の側面に平行になるように（通常は水平に）画像が位置合わせされます。 さらに、座標（ x ₀ 、 y ₀ ）を持つ点に対して、対応するエピポーラ線が方程式x = x ₀で与えられるように画像が整列され_ます 。次に、各点について、対応するペア点を2番目の画像と同じ線で検索する必要がありますカメラ。 この画像調整プロセスは、修正と呼ばれます。 通常、修正は画像の再イメージングによって実行され、歪みを取り除くことと組み合わされます。 修正された画像の例を図3に示します。画像は、深度マップhttp://vision.middlebury.edu/stereoを構築するためのさまざまな方法を比較する画像のデータベースから取得されます。

図3：修正された画像と対応する視差マップの例

画像を修正した後、対応するポイントのペアを検索します。 最も簡単な方法は図4に示されており、以下から構成されています。 座標（ x ₀ 、 y ₀ ）を持つ左画像の各ピクセルについて、右画像でピクセル検索が実行されます。 右の画像のピクセルは座標（ x ₀ - d 、 y ₀ ）を持つ必要があると想定されます。ここで、 dは視差と呼ばれる値です。 対応するピクセルの検索は、応答関数の最大値を計算することで実行されます。応答関数は、たとえば、ピクセル近傍の相関です。 その結果、視差マップが作成されます。その例を図に示します。 3。

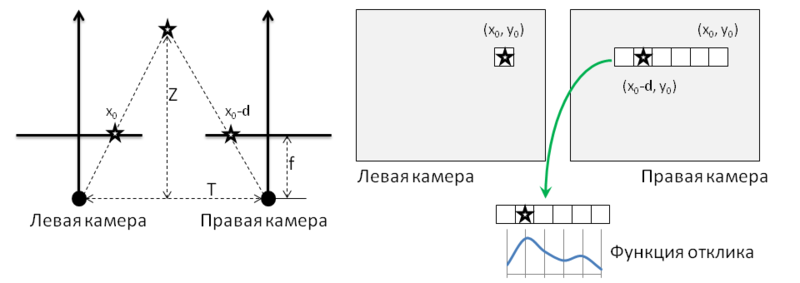
図4：深度マップの計算。

実際の深度値は、ピクセル変位の大きさに反比例します。 図4の左半分の表記を使用すると、視差と深度の関係は次のように表現できます。

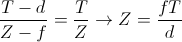
深さと変位の逆の関係により、この方法に基づいて機能するステレオビジョンシステムの解像度は、近距離ではより良く、遠距離ではより悪くなります。